基于风险偏好差异性假设的动态决策过程研究①

刘　健， 陈　剑， 廖文和， 马义中， 刘思峰

(1. 南京理工大学经济管理学院， 南京 210094； 2. 清华大学经济管理学院， 北京 100084；3. 南京理工大学机械工程学院， 南京 210094； 4. 南京航空航天大学经济与管理学院， 南京 211106)



基于风险偏好差异性假设的动态决策过程研究①

刘健1, 2， 陈剑2， 廖文和3， 马义中1， 刘思峰4

(1. 南京理工大学经济管理学院， 南京 210094； 2. 清华大学经济管理学院， 北京 100084；3. 南京理工大学机械工程学院， 南京 210094； 4. 南京航空航天大学经济与管理学院， 南京 211106)

针对风险偏好差异性决策者共存时的决策过程进行研究，提出边求解边对决策者分类决策再进行信息融合的动态决策策略. 从客观数据角度基于属性值相似关系提取有效属性并对有效属性进行赋权；根据决策者对决策活动的选择判断逐步嵌入风险偏好(风险偏好型、风险中立型、风险规避型)；基于属性值之间的可能度与相似度，构建相应类型的风险偏好预期理论模型；在决策信息集结与决策对象排序过程中，根据决策者的风险偏好特征选择相适应的算法模型；针对风险偏好差异性决策者共存的情形，基于决策结果公平效用最大化的角度提出新的信息融合模型构建算法；通过实际案例进行分析并验证这一新方法的科学合理性.

差异性； 风险偏好； 动态策略； 公平效用； 决策过程

0　引　言

本文针对风险偏好差异性决策者面对含有大量数据的决策问题进行研究，风险偏好差异性势必会对决策过程(如：有效属性的提取、属性赋权、信息集结、排序择优)产生一定影响，并产生一些新的特征，需要对这些新的特征进行深入研究. 决策表中出现大量的数据主要包括三种情形[1]：1)大量的决策属性，有限的决策对象；2)大量的决策对象，有限的决策属性；3)以上两种情形都存在. 本文针对第一种情形，研究基于决策者风险偏好差异性假设的动态决策过程，提出边求解边对决策者分类决策再进行信息融合的动态决策策略，用以解决风险偏好差异性决策者共存时的复杂决策问题.

边求解边对决策者分类决策再进行信息融合的动态决策策略，首先从客观数据角度出发，利用基于属性值相似关系的属性约简算法提取有效属性并通过相似关系辨析矩阵对有效属性进行赋权，然后嵌入决策者的风险偏好(风险规避型、风险中立型、风险偏好型)，在信息集结与决策排序过程中选择与风险偏好相对应的模型算法，该决策策略能够一边进行决策任务的分解，一边根据决策者风险偏好对其进行分类决策，在此过程中针对属性值为区间数的决策问题，提出基于可能度与相似度度量的风险偏好预期理论模型，最后，基于决策结果公平效用最大化角度提出基于新的信息融合模型构建算法.

随着信息科技的发展，如何从大量数据中提取有效信息进行决策，是一个非常重要的研究内容，也是决策科学领域所面临的一个重要挑战[2-3]. 属性约简[4-6]技术是从大量信息中获取有用知识的一个基本方法. 本文将属性约简的技术引入含有大量属性的决策问题是从易于决策者在规定的时间内进行科学合理决策的角度进行考虑的，这就需要基于决策者的风险偏好特征并结合决策数据本身特点，选择一种适合的约简算法. 研究发现，从含有大量属性的决策数据表中提取有效属性过程，决策者的态度分为两类：1)决策者的风险偏好对有效属性的提取起到非常重要的作用，不同风险偏好决策者从同一个决策表中会提取不同的有效属性；2)决策者的风险偏好对决策对象的排序与选择过程有关，但与有效属性的选择与赋权无关，有效属性的选择与赋权应从客观数据的角度出发[6]. 文献[7-10]研究了决策者风险偏好对决策结果的影响，文献[1]针对决策者的风险偏好影响有效属性的提取，以决策表中含有大量决策属性和有限决策对象的问题为背景进行研究，提出先对决策者分类再进行决策的策略，根据决策者的风险偏好特征[7,11-12]将其分类(风险偏好型、风险中立型、风险规避型)，针对不同风险偏好类型的决策者构建相应的优势关系预期理论模型；提出基于优势关系辨析矩阵的属性约简与属性赋权算法；基于属性值优势度矩阵解决信息融合与决策对象排序问题，针对不同风险类型的决策者分类决策.

针对决策者的风险偏好不影响有效属性的选择与赋权，仅影响决策对象的排序与选择，从客观数据角度仅依据相同属性上两个属性值之间的关系，提出基于属性值相似关系的属性约简算法，若属性值为实数的决策表，当两个决策对象在同一个属性上的属性值相同时，该属性对于比较这两个决策对象是不起作用的，从而该属性是冗余属性. 针对属性值为区间数的决策表，当两个属性值为区间数的决策对象在某个属性上的信息相似度(信息重合程度)达到某个标准时(如：80%或90%)对于决策者来说这两个属性值提供相同的决策信息，此时该属性对于决策者区分这两个决策对象也是不起作用的，那么该属性也是冗余属性，基于以上所述，在决策过程中可删除决策表中的冗余属性. 因为两个区间数之间的相似度大小不会随决策者的风险偏好发生变化，因此利用基于属性值相似关系的算法进行属性约简提取有效属性时，不用提前根据决策者的风险偏好特征对其进行分类，因此在本文提出的动态决策策略中，首先进行属性约简，然后对有效属性进行赋权，但是属性权重的确定应与属性约简算法的思想一致. 由于区间数的特殊性，针对属性值为区间数的决策问题，本文中给出一种新的区间数相似度定义，确定两个属性值之间信息的相似度.

属性权重确定与信息集结也是多属性决策问题中一个重要的研究内容，目前针对属性权重未知的多属性决策问题，属性权重的确定方法可归结为主观赋权法[1,13-15]，客观赋权法[7,16-18]，主客观赋权法[19-22]等. 本文将属性约简引入含有大量属性的决策问题并将其作为决策过程的第一步，提出基于属性值相似关系属性约简算法，因此在对有效属性赋权时需要采用与基于相似关系的属性约简算法相吻合的算法，用以保证决策子过程算法思想的一致性，基于此本文提出基于相似关系辨析矩阵的属性赋权算法. 由于决策者的风险偏好影响决策对象的排序与选择过程，从而在属性约简与有效属性赋权后，在决策过程中逐步嵌入决策者的风险偏好，在信息集结与决策对象排序[23-24]过程中，构建与风险偏好相对应的基于可能度与相似度度量的预期理论模型，确定属性值之间的优势关系，选择与决策者风险偏好相对应的算法分类决策.

本文创新之处：针对风险偏好差异性决策者面对含有大量决策属性的决策问题，提出边求解边对决策者分类决策再进行信息融合的动态决策策略及与策略相应的算法模型，首先，从客观数据角度利用基于属性值相似关系的属性约简算法构造相应的辨析矩阵，利用辨析函数通过辨析矩阵提取有效属性；其次，利用基于相似关系辨析矩阵对有效属性进行赋权，然后，根据决策者的风险偏好特征进行分类(风险规避型、风险中立型、风险偏好型)并将决策者的风险偏好嵌入决策过程，选择与风险偏好特征对应的算法进行信息集结、在此过程中，构建与风险偏好相对应的预期理论模型，确定属性值之间的优势关系，在此基础之上，利用综合加权优势度矩阵对决策对象排序择优，最后，针对风险偏好差异性决策者共存时的情形，基于决策结果公平效用最大化提出新的信息融合模型及排序算法.

1　大数据表决策问题

根据文献[16]可知任意实数都可用区间数进行表示，本文以决策表中含有大量属性且属性值为区间数的决策问题为例进行研究.

1.1含有大量属性且属性值为区间数的决策问题

复杂产品研制过程最优质量管理控制方案的选择问题：假设在欧盟第七框架QB50项目双单元标准大气探索某立方星的研制过程中，经初步筛选后有5个质量管理控制方案入围，分别用U={A1,A2,A3,A4,A5}来表示，若邀请100位专家对所有入围方案，在每个指标上的现状进行投票. 假如每位专家对每个入围方案在相应指标上的现状进行投票，投票分为赞成票、反对票、弃权票3种情形，那么当赞成票与反对票的人数之和相加不到100时，就说明有专家在该指标上投了弃权票. 用专家数减去投反对票的数，获得的数据表示该决策方案在某个指标上可能的最大赞成票数，最终的赞成票数分布在投赞成票人数与可能的最大赞成票数之间(本文假设区间内任何一点的分布是相同的)，根据文献[16]中关于区间数的基础知识可知，该决策问题中的属性值就可以用区间数来进行表示，如表1所示，请根据表1中的数据做出最优选择方案.

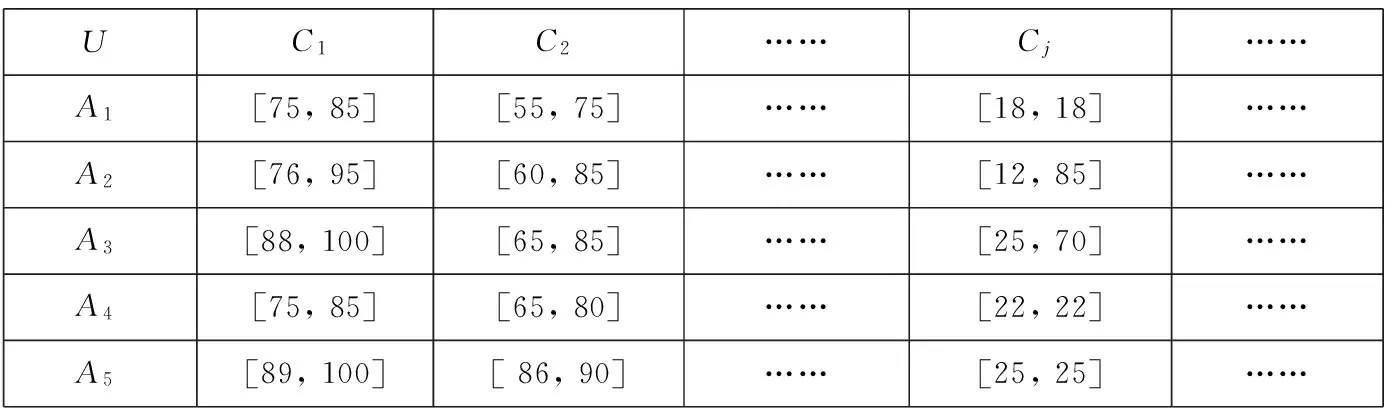
表1　100位专家投赞成票的可能分布情况

显然，决策表1中含有大量的决策属性且属性值是区间数，若要求决策者利用属性约简算法从表1中提取有效属性进行决策，那么如何选择合适的属性约简算法从表1中提取有效属性是本文研究的重点.

1.2区间数基础知识

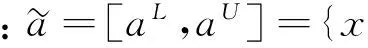
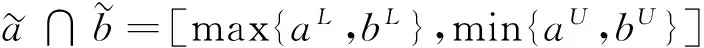
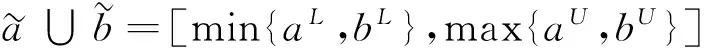
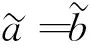
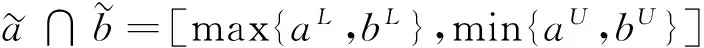
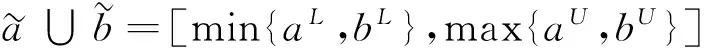
(1)

由定义2可知：区间数相似度是两个区间数之间相同信息量覆盖区间与可能信息量覆盖区间之间取值长度的比值，也是相同信息的重合程度.

1.3属性约简的原则和方法

在表1中决策对象A3,A5在属性C1上的属性值分别是[88, 100]与[89, 100]，根据法则3可知，这两个区间数不相等. 根据区间数相似度的定义2可知，这两个区间数之间的相似度达到11/12=0.916 7，也就是说决策对象A3,A5在属性C1上的两个属性值之间共同信息与可能信息的取值区间重合覆盖程度达到91.67%. 针对含有大量属性且属性值为区间数的决策问题，由于区间数在其区间内每个点上的概率均为1，那么决策者认为当两个决策对象在同一属性上的属性值并不一定需要完全相同，当其属性值之间的相似度达到一定标准(程度)(如：80%或90%)时，这两个决策对象在该属性上对于决策者提供相同的信息，该属性对于决策结果的改变不起作用，那么可以将其作为不必要的决策属性，从决策表中删除，同时在对决策对象进行排序时，当两个区间数之间的相似度达到一定程度时，决策者同样认为二者是等价的. 根据上面的假设分析，属性C1对于区分决策对象A3,A5是不起作用的，但决策对象A1,A3在属性C1上的相似度为0，从而属性C1对于区分A1,A3是起作用的，因此需要对决策表中的所有决策对象进行分析，构建相应的辨析矩阵，利用相应算法提取整个决策表中的有效属性.

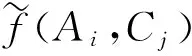
(2)

有效属性的获取：本文通过辨析函数[26-27]从辨析矩阵中提取有效属性.

(3)

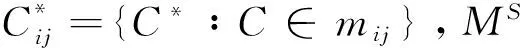
本文提出的基于属性值相似关系的属性约简算法与文献[1]中提出的基于属性值之间优势关系的属性约简算法的原则和方法不同. 当某个决策对象相对于其他决策对象在某个属性上具有较大优势时，按照本文提出的约简算法，该属性一定作为元素出现在辨析矩阵中，从而该属性有可能会成为有效属性，但是当该属性相对于其他所有决策对象在该属性上占优势时，根据式(3)可知，该属性一定是有效属性，因为此时其他决策对象的属性值与该决策对象的属性值在该属性上的相似度均达不到指标约简的标准αj(j∈1,2,…,m).

文献[1]中提出的基于属性值之间优势关系的属性约简算法，当某个决策对象相对于其他决策对象在某个属性上的属性值占优时，该属性是辨析矩阵中的相应位置的元素(即当两个属性值在某个属性上不相等时，该属性就可以作为辨析矩阵中的相应元素)，从而其属性约简标准比基于属性值之间相似关系的约简标准低，因此本文提出的基于相似关系的约简算法比基于属性值之间优势关系约简算法，进行有效信息提取时丢失的信息少. 为验证上述观点，本文接下来将对属性值之间的优势关系进行详细介绍，同时在最后将本文中提出的属性值相似关系属性约简算法及赋权算法与文献[1]中基于属性值之间优势关系的属性约简算法与赋权算法的决策结果进行比较分析.

1.4有效属性赋权

在辨析矩阵中出现次数越多的属性，说明在该属性上属性值之间的相似度达不到约简标准的越多，从而在该属性上属性值差异比较大的决策对象越多，因此该属性在矩阵中出现的次数越多，就说明决策者应该考虑的次数就越多，那么其相应的权重应越大. 根据基于优势关系的赋权算法[3,7]、基于相似关系的赋权算法[25]和基于离差最大化的赋权算法[16]可知属性值之间的差异越大，该属性的权重应该越大，因此本文提出的属性赋权算法与文献中[3,7,16,25]中的赋权算法在本质上出发点是一致的. 基于相似关系辨析矩阵的赋权算法与文献[1]中基于优势关系辨析矩阵赋权算法的理论基础虽不同，但出发点一致，即在辨析矩阵中出现次数越多的属性权重应越大.

根据上述描述，基于相似关系辨析矩阵的有效属性赋权算法如式(4)所示

(4)

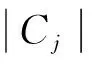
1.5信息融合及预期理论模型

本文利用文献[1]中提出的综合加权优势度矩阵(weighted advantage degree matrix, WADM)结合决策者相应的风险偏好特征(risk type, RT)对决策对象进行排序算法如式(5)―式(8)所示

(5)

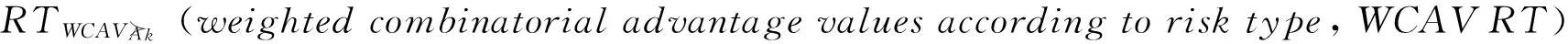
(6)

根据各个决策对象的综合优势度值对决策表中所有的决策对象进行排序并择优.

其中dA1≻A2表示决策对象A1与A2相比的加权综合优势度值，那么

dA1≻A2=dA1≻A2/C1·ω1+…+dA1≻A2/Cm'·ωm′

(7)

当dA1≻A2>0时，表示决策对象A1≻A2.

dA1≻A2/C1表示决策对象A1与A2相比在属性C1上的优势度值，将属性之间的优势关系用优势度值表示如式(8)所示

(8)

根据前景理论[28-29]可知，不同风险偏好决策者对于具有相同期望值的不同属性值之间优势关系的态度是不同的，本文提出的边求解边对决策者分类决策再进行信息融合的动态决策策略，在对决策信息集结与决策对象排序过程时必须考虑决策者的风险偏好类型. 本文针对三种类型的风险偏好决策者(风险规避型(risk-aversion, RA)、风险中立型(risk-neutral, RN)、风险偏好型(risk-seeking, RS))，提出利用区间数可能度与相似度度量的预期理论模型进行优势关系的确定. 虽然不同的决策者对风险的偏好程度大小不同，但所有的决策者都属于上述三种类型中的一种，本文假设所有决策者的风险偏好类型已知，风险偏好差异性是指决策者中同时存在两种或两种以上不同风险偏好类型的决策者.

本文在式(2)中利用αj(j∈1,2,…,m)作为属性约简标准，当两个区间数之间的相似度大于或等于αj(j∈1,2,…,m)时，这两个属性对于决策者而言提供相同的决策信息，也就是其属性值之间具有等价关系.

根据区间数定义可知，具有相同可能度的不同区间数其信息的覆盖区间是不同的. 由几个确定的区间数所构成的理想区间数也是固定的，根据区间数相似度定义，不同区间数与同一个固定的理想区间数之间的相似度不同. 若决策对象与正理想对象的相似度越大，该决策对象与正理想对象之间的共同信息就越大，该对象就更优；若决策对象与负理想对象的相似度越小，该对象与负理想对象之间的共同信息就越小，该对象更优.

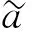
(9)

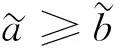
文献[16]给出了区间数可能度的另一种表达方式，如定义6所示.

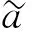
(10)

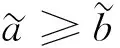
文献[20]已证明式(9)与式(10)两种可能度表达式之间的等价关系.

利用区间数之间可能度与相似度度量的风险偏好预期理论模型如下所示：

风险规避型预期理论模型1

(11)

风险中立型预期理论模型2

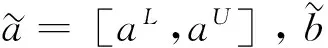
(12)

风险偏好型预期理论模型3

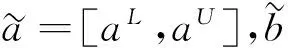
(13)

根据上述三个不同的预期理论模型可知，当某个决策对象的相对于其他决策对象在某个属性上具有较大优势时，两个属性值之间不存在等价关系，从而两个属性值之间的相似度达不到指标约简的标准，按照基于相似关系的属性约简算法，根据式(2)和式(3)可知该属性一定是辨析矩阵中的相应元素，有可能是有效属性.

针对同一个决策问题，从不同的角度出发进行描述会得到完全相反的结果. 上述问题中的关键点在于决策者对投弃权票人群的看法，若决策者认为弃权者未来会投赞成票，那么目前反对票最少的就是最好的；若决策者认为弃权者未来会投反对票，那么目前获得赞成票最多的就是最好的；判定决策者认为弃权者未来是投反对票还是投赞成票，是由决策者的心态所决定的. 针对相比具有相同可能度(期望值)而不同情形下的决策行为，若决策者凡事均往坏处想，对未来抱有悲观的态度，该决策者明显属于风险规避型，则该决策者在决策中会选择目前赞成票最高的作为最优对象，若决策者总是想着好的发展方向，对未来风险抱有乐观的态度，该决策者明显是风险偏好型，那么未来最优的是最好的.

面对同样的决策问题，不同的风险偏好决策者可能会得到不同的结果，这说明决策者的风险偏好是影响决策对象排序的重要因素. 上述任何一种排序结果都是科学合理的，都可以满足某一类(风险规避型、风险中立型、风险偏好型)风险偏好决策者的需求. 虽然在实际决策中每个决策者对风险的偏好程度的大小不同，但所有的决策者都可归为上述三种风险偏好类型. 那么在决策中存在上述两种或两种以上风险偏好类型的决策者时，如何进行决策或信息融合是值得研究的问题，将在下一节中对此进行介绍.

1.6基于偏好差异性的信息融合模型构建

在1.5中针对不同风险偏好类型的决策者提出了基于加权综合优势度值的决策对象排序算法. 若不同风险偏好类型的决策者均参与决策过程，如何对决策对象进行排序是个重要的研究问题. 本文针对风险偏好差异性决策者共存情形提出基于决策结果公平效用[30-33]最大化的信息融合算法.

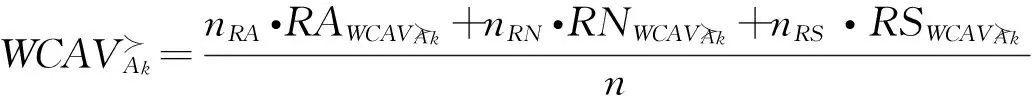
(14)

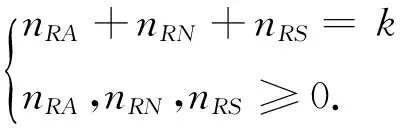
2　基于风险差异性假设的动态决策过程

现行的决策算法，对决策问题的求解是没有过属性约简获取有效属性这个步骤，本文在决策过程求解中均考虑上述步骤，并将其嵌入决策过程作为决策过程的第一步，那么就要对现行的传统决策问题求解步骤进行调整.

基于决策者差异性假设的动态决策过程，边求解边对决策者分类决策再进行信息融合的动态决策策略步骤如下.

步骤1属性约简

针对含有大量属性的决策数据表利用基于属性值相似关系的属性约简算法构造辨析矩阵，利用辨析函数提取有效属性.

步骤2属性赋权

针对有效属性利用基于相似关系辨析矩阵进行属性赋权.

步骤3偏好嵌入与分类决策

根据决策者的风险偏好特征，对决策者进行分类，选择相应算法进行信息集结、排序与择优.

步骤4偏好差异性共存情形的信息融合

偏好差异性决策者共存时基于决策结果公平效用最大化的信息融合模型构建与决策对象排序.

步骤5验证与分析

决策结果验证与分析.

3　基于风险偏好差异性的多属性决策案例

欧盟第七框QB50项目双单元标准大气探索某立方星研制过程最优质量管理控制方案的选择问题：假设针对初期入围的5个质量管理控制方案，分别用U={A1,A2,A3,A4,A5}来表示，若决策者需要考虑C={C1,C2,C3,C4,C5,C6,C7,C8,C9}，过程能力指数(零部件质量)C1，风险C2，可靠性C3，成本(返修、加工、研发)C4，可行性C5，时间C6，投资回报率C7，零部件装配能力C8，顾客满意度C9等9个属性. 假如100位专家，对每个入围方案在所有指标上的现状进行投票，投票分为赞成票、反对票、弃权票3种，根据表2中每个入围方案在各个指标上最终赞成票的可能分布情况结果做出最优选择？

表2　100位专家最终赞成票可能分布情况 (9个指标)

针对决策表2中的数据，本文假设决策者在决策表中所有指标上的约简标准值是相同的，当两个决策对象的属性值在同一个属性上的相似度达到85%时，对决策者来说该属性是提供相同的决策信息. (约简标准为85%)

步骤1属性约简

根据式(1)和(2)可知，基于相似关系的辨析矩阵为对称矩阵，本文仅给出该矩阵的上三角部分，那么在所有属性上的约简标准均为85%时，基于相似关系的辨析矩阵如下所示

通过辨析函数[26-27]从辨析矩阵中提出有效属性，可得{C1,C2,C3,C4,C7,C8}是决策表2中一组有效属性，因此利用表2中的决策信息对决策对象排序择优时，{C1,C2,C3,C4,C7,C8}这6个属性是必需要考虑的有效属性(原决策表有9个属性)，那么其余的3个属性{C5,C6,C9}是可以忽略的.

针对属性值为区间数的决策问题，利用基于属性值相似关系的算法进行属性约简提取有效属性时，不用根据决策者风险偏好特征进行分类，因为两个区间数之间的相似度不会因为决策者风险偏好类型的变化而改变. 从而无论对哪种风险偏好类型的决策者，利用基于区间数相似关系的属性约简算法，都会得到相同的有效属性.

步骤2属性赋权

利用式(4)对有效属性进行赋权，各个属性的权重为

步骤3偏好嵌入与分类决策

针对决策者的风险偏好影响决策对象的排序与选择过程，因此在对有效属性提取与赋权后，应在该步骤中根据决策者对决策活动的选择判断嵌入决策者的风险偏好.

1)若决策者为风险规避型

对决策表2中的数据，利用有效属性{C1,C2,C3,C4,C7,C8}，根据式(5)、(7)、(8)、(11)构造决策对象加权综合优势度矩阵为WADM=

针对风险规避型决策者，由式(6)可得各个决策对象综合优势度值为

根据各个决策对象的综合优势度值，针对风险规避型决策者决策对象排序结果为

所以，A5是最优决策对象.

2)若决策者为风险中立型

对决策表2中的数据，利用有效属性{C1,C2,C3,C4,C7,C8}，根据式(5)、(7)、(8)、(12)构造决策对象加权综合优势度矩阵为

WADM=

根据各个决策对象的综合优势度值，针对风险中立型决策者决策对象排序结果为

因为dA4≻A2=-1/54<0, 可知A2≻A4, 所以经过综合与局部结果调整后的排序结果应为

所以，A5是最优决策对象.

3)若决策者为风险偏好型

对决策表2中的数据，利用有效属性{C1,C2,C3,C4,C7,C8}，根据式(5)、(7)、(8)、(13)构造决策对象加权综合优势度矩阵为

WADM=

针对风险偏好型决策者，由式(6)可得各个决策对象综合优势度值为

根据各个决策对象的综合优势度值，针对风险偏好型决策者决策对象排序结果为

所以，A5是最优决策对象.

4)偏好差异性决策者共存情形

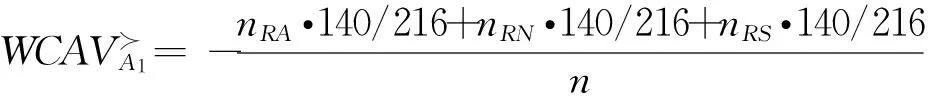
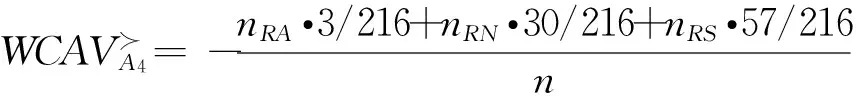
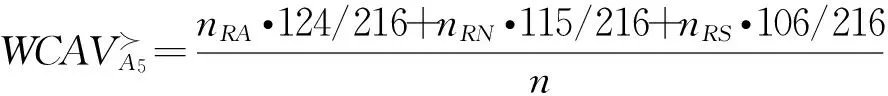
当三种风险偏好类型的决策者均参与决策，且每种偏好类型决策者的人数相同时，根据基于决策结果公平效用最大化的决策对象加权综合优势度值，决策对象排序结果为

A5≻A3≻A4≻A2≻A1

所以，A5是最优决策对象.

4　决策结果验证与分析

4.1基于优势关系属性约简与赋权算法验证

利用文献[1]中提出的基于属性值之间优势关系的属性约简与赋权算法，构造辨析矩阵并通过辨析函数提取有效属性，利用基于优势关系的辨析矩阵对有效属性进行赋权，然后构建基于属性值之间优势关系的综合加权优势度矩阵进行信息集结，对决策对象进行排序择优.

1)若决策者为风险规避型

利用文献[1]中的相关算法，针对决策表2中的数据，可以到相应的基于属性值之间优势关系的辨析矩阵为

利用辨析函数可得{C1,C2,C3,C4,C8,C9}是一组有效属性(含有6个属性，原数据表中有9个属性). 利用有效属性{C1,C2,C3,C4,C8,C9}进行决策，针对决策表2中的数据可以得到

所以，A5是最优决策对象.

利用文献[1]中的相关算法，针对决策表2中的数据，可以到相应的基于属性值之间优势关系的辨析矩阵为

利用辨析函数可得{C1,C2,C3,C4,C8,C9}是一组有效属性(含有6个属性，原数据表中有9个属性). 利用有效属性{C1,C2,C3,C4,C8,C9}进行决策，针对决策表2中的数据可以得到

所以，A5是最优决策对象.

当决策者为风险中立型，针对决策表2中的数据利用本文基于属性值相似关系的属性约简算法提取有效属性进行决策与文献[1]中基于属性值之间优势关系的属性约简算法提取有效属性并进行决策，虽然得到不同的排序结果，但得到完全相同的最优决策对象.

3)若决策者为风险偏好型

利用文献[1]中的相关算法，针对决策表2中的数据，可以得到基于属性值之间优势关系的辨析矩阵为

利用辨析函数可得{C1,C2,C3,C4,C6,C7,C8,C9}是一组有效属性. 利用这一组有效属性进行决策，针对决策表2中的数据可以得到

所以，A5是最优决策对象.

当决策者为风险偏好型，针对决策表2中的数据利用本文基于属性值相似关系的属性约简算法提取有效属性进行决策与文献[1]中基于属性值之间优势关系的属性约简算法提取有效属性进行决策，虽然得到不同的排序结果，但得到完全相同的最优决策对象.

4)偏好差异性决策者共存情形

若在决策中三种风险偏好类型的决策者数量恰好相等，即nRA=nRN=nRS时. 基于决策结果公平效用最大化的信息融合算法，对决策表2中的决策对象排序为

A5≻A3≻A4≻A2≻A1

所以，A5是最优决策对象.

当偏好差异性决策者共存时(两种或两种以上风险偏好差异性决策者共存)，针对决策表2中的数据利用本文基于属性值相似关系的属性约简算法提取有效属性进行决策与文献[1]中基于属性值之间优势关系的属性约简算法提取有效属性进行决策，得到完全相同的排序结果与最优决策对象.

4.2有效属性与所有属性决策结果比较验证

对决策表2中的数据，利用式(4)及第三部分中的辨析矩阵对所有属性进行赋权得

1)若决策者为风险规避型

由式(5)、(6)、(7)、(8)、(11)，针对决策表2的决策对象得

所以，A5是最优决策对象.

当决策者为风险规避型，针对决策表2中的数据利用有效属性与利用所有属性进行决策，得到完全相同的最优决策对象，但是所得的排序结果有所不同.

2)若决策者为风险中立型

由式(5)、(6)、(7)、(8)、(12)，针对决策表2中的决策对象得

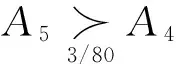
所以，A5是最优决策对象.

当决策者为风险中立型，针对决策表2中的数据利用所有属性与有效属性进行决策，虽得到不同的排序结果，但得到相同的最优决策对象.

3)若决策者为风险偏好型

由式(5)、(6)、(7)、(8)、(13)，针对决策表2的决策对象得

所以，A3是最优决策对象.

当决策者为风险偏好型，针对决策表2中的数据利用所有属性与有效属性进行决策，得到不同的排序结果与不同的最优决策对象.

4)偏好差异性决策者共存情形

若在决策中三种风险偏好类型的决策者数量恰好相等，即nRA=nRN=nRS时. 根据基于决策结果公平效用最大化的信息融合算法，决策表2中的决策对象排序结果为

A5≻A4≻A3≻A2≻A1

所以，A5是最优决策对象.

当三种风险偏好类型决策者共存时，针对决策表2中的数据利用有效属性与所有属性进行决策，虽得到不同的排序结果，但得到完全相同最优决策对象.

4.3决策结果比较

针对4.1节的结果：当某个决策对象相对于其他决策对象在某个属性上具有较大优势时，按照本文提出的基于属性值相似关系的属性约简算法与文献[1]中基于属性值之间优势关系的属性约简算法，对决策表2中的数据分别提取有效属性，利用有效属性进行决策，在上述四种情形中：两种情形(风险规避型决策者、偏好差异性决策者共存)，得到完全相同的排序结果与最优决策对象；两种情形(风险中立型决策者、风险偏好型决策者)，虽得到不同的排序结果，但得到完全相同的最优决策对象. 从而说明本文针对决策表中含有大量属性的决策问题，提出基于属性值相似关系属性约简算法的科学合理性.

针对4.2节的结果：利用决策表中的所有属性与属性约简后的有效属性进行决策，在上述四种情形中：一种情形(风险规避型决策者)，得到完全相同的排序与最优决策对象；两种情形(风险中立型决策者、偏好差异性决策者共存)，虽然得到不同的排序结果，但得到完全相同的最优决策对象；一种情形(风险偏好型决策者)，得到不同的排序结果，同时也得到不同的最优决策对象，由于风险偏好型决策者的特征，该类型决策者完全可接受不同的决策结果，根据前景理论可知在现实生活中风险规避型决策者占多数，风险偏好型决策者在决策中仅占少数，同时决策者在实际决策过程中对最优决策对象的关注远远大于对决策对象排序结果的关注程度.

针对4.1节与4.2节的决策结果可知：当三种风险偏好决策者的人数相同时，决策对象的加权综合优势度值与风险偏好中立型决策者所得结果完全相同. 在上述两节中针对风险规避型决策者，都得到完全相同的排序结果与最优决策对象，根据前景理论可知在现实生活中风险规避型决策者占多数，虽然面对不同决策问题，决策者对风险的规避程度大小不同，但不影响决策者的风险偏好类型，从而说明本文提出算法的科学合理性.

4.4决策结果分析

决策者的风险偏好类型不同，面对相同数据表不同风险偏好决策者得到不同的排序结果是科学合理的. 针对4.1节和4.2节中相同偏好类型的决策者，得到相同的最优决策对象与不同的排序结果，本文认为存在以下三个方面的原因：

1)决策对象本身不可比. 决策者无法在决策信息表中，找到一个决策对象在所有属性上都比其他决策对象相比占优势，在多属性决策问题中，当某个决策对象的绝大多数属性上都比其他的决策对象占优势，仅在某个或某几个属性上处于劣势，仍然不能确定该决策对象就比其他决策对象占优势.

2)属性约简标准的确定问题. 针对决策表2中的数据进行属性约简时，本文中以相似度85%作为属性约简的标准，可能它比实际的有效值偏低，决策者应该多次尝试找到更好的有效值，因此采用合适的约简标准提取有效属性进行决策，能够有效提高决策对象排序结果的一致性，进一步提高决策的质量.

3)风险偏好差异性决策者比重的确定. 不同风险类型决策者共存时，对决策对象排序需要进行利益协调与规则制定，决策者应尽可能照顾各方的利益对决策信息进行融合，根据前景理论可知在实际决策中三类风险偏好类型的决策者人数不同，本文假设三种类型决策者人数相同，因此人数比重的确定也影响决策对象的排序结果.

本文在案例应用中仅选择含有9个属性的属性值为区间数的决策问题，通过两种不同的方法用四种情形分别验证算法的有效性，但本文是针对风险偏好差异性决策者面对决策表中含有大量属性的决策问题为研究背景，提出边求解边对决策者分类决策再进行信息融合的动态决策策略及与策略相对应的算法模型，因此本文提出的动态决策算法为决策表中含有大量属性决策问题的解决也提供了一种科学有效的方法.

5　结束语

本文针对风险偏好差异性决策者共存时的动态决策过程进行研究. 通过含有大量决策属性的属性值区间数的不确定决策问题为研究背景，将属性约简技术与决策者的风险偏好相结合，为问题的解决找到了一种科学合理有效的决策方法.

本文主要做了五个方面的工作：1)提出边求解边对决策者分类决策再进行信息融合的动态决策策略及与策略相对应的算法模型，从客观角度基于属性值相似关系构建辨析矩阵提取有效属性，基于相似关系辨析矩阵对有效属性进行赋权；2)根据决策者对决策活动的选择判断嵌入决策者偏好，针对决策者的风险偏好类型采用相应的算法模型，一边进行决策任务的分解与信息集结，一边根据决策者偏好对其进行分类决策；3)通过构建基于区间数相似度与可能度度量的风险偏好预期理论模型(风险规避型、风险中立型、风险偏好型)，确定属性值之间的优势关系，利用综合加权优势度矩阵对决策对象进行排序择优；4)针对两种及两种以上风险偏好差异性决策者共存情形，提出基于决策结果公平效用最大化的信息融合模型算法；5)通过对比利用有效属性进行决策与利用决策表中所有属性进行决策、以及本文算法与基于属性值之间优势关系属性约简与属性赋权算法进行决策结果的比较验证分析，说明本文提出算法的有效性与科学合理性.

未来将对基于决策者差异性假设的新偏好模型构建算法，群决策中公平效用平衡点的求解，决策流程与决策者之间社会关系网络推理等问题进行深入研究.

[1]刘健, 陈剑, 刘思峰, 等. 风险偏好与属性约简在决策问题中的应用研究[J]. 管理科学学报, 2013, 16(8): 68-79.

Liu Jian, Chen Jian, Liu Sifeng, et al. Risk preferences and attribute reduction in decision making problems[J]. Journal of Management Sciences in China, 2013, 16(8): 68-79. (in Chinese)

[2]James S D, Peter C, Fish B, et al. Multiple criteria decision making, multi-attribute utility theory: The next ten years[J]. Management Science, 1992, 38(5): 645-654.

[3]Jyrki W, James S D, Peter C, et al. Multiple criteria decision making, multiattribute utility theory: Recent accomplishments and what lies ahead[J]. Management Science, 2008, 54(7): 1336-1349.

[4]Guan Y Y, Wang H K. Set-valued information systems[J]. Information Sciences, 2006, 176(17): 2507-2525.

[5]Zdzistaw P, Skowron A. Rough sets: Some extensions[J]. Information Sciences, 2007, 177(1): 28-40.

[6]张文修, 仇国芳. 基于粗糙集的不确定决策[M]. 北京： 清华大学出版社， 2005.

Zhang Wenxiu, Qiu Guofang. Uncertain Decision Making Based on Rough Sets[M]. Beijing: Tsinghua University Press, 2005. (in Chinese)

[7]Liu J, Liu S F, Liu P, et al. A new decision support model in multi-criteria decision making with intuitionistic fuzzy sets based on risk preferences and criteria reduction[J]. Journal of the Operational Research Society, 2013, 64(8): 1205-1220.

[8]刘咏梅, 卫旭红, 陈晓红. 群体情绪智力对群决策行为和结果的影响研究[J]. 管理科学学报， 2011， 14(10): 11-27.

Liu Yongmei, Wei Xuhong, Chen Xiaohong. The effects of group emotional intelligence on group decision-making behaviors and outcomes[J]. Journal of Management Sciences in China, 2011, 14(10): 11-27. (in Chinese)

[9]Amos T, Daniel K. The framing of decisions and the psychology of choice[J]. Science, 1981, 211(4481): 453-458.

[10]Platt B C, Price J, Tappen H. The role of risk preferences in pay-to-bid auctions[J]. Management Science, 2013, 59(9): 2117-2134.

[11]Podinovski V V. Set choice problems with incomplete information about the preferences of the decision maker[J]. European Journal of Operational Research, 2010, 207(1): 371-379.

[12]Henderson V. Prospect theory, liquidation, and the disposition effect[J]. Management Science, 2012, 58(2): 445-460.

[13]Zhang J J, Wu D S, Olson D L. The method of grey related analysis to multiple attribute decision making problems with interval numbers[J]. Mathematical and Compute Modelling, 2005, 42 (9): 991-998.

[14]Saaty T L. The modern science of multi-criteria decision making and its practical applications: The AHP/ANP approach[J]. Operations Research, 2013, 61(5): 1101-1118.

[15]Fan Z P, Feng B, Jiang Z Z, et al. A method for member selection of R&D teams using the individual and collaborative information[J]. Expert Systems with Applications, 2009, 36(4): 8312-8323.

[16]徐泽水.不确定多属性决策方法及应用[M]. 北京： 清华大学出版社， 2004.

Xu Zeshui. Uncertain Multiple Criteria Decision Making Methods and Applications[M]. Beijing: Tsinghua University Press, 2004. (in Chinese)

[17]徐泽水, 孙在东. 一类不确定型多属性决策问题的排序方法[J]. 管理科学学报, 2002, 5(3): 35-39.

Xu Zeshui, Sun Zaidong. Priority method for a kind of multi-attribute decision-making problems[J]. Journal of Manegement Sciences in China, 2002, 5(3): 35-39. (in Chinese)

[18]Danielson M, Ekenberg L. Augmenting ordinal methods of attribute weight approximation[J]. Decision Analysis, 2014, 11(1): 21-26.

[19]徐泽水. 基于方案达成度和综合度的交互式多属性决策法[J]. 控制与决策, 2002, 17(4): 435-438.

Xu Zeshui. Interactive method based on alternative achievement scale and alternative comprehensive scale for multi-attribute decision making problems[J]. Control and Decision, 2002, 17(4): 435-438. (in Chinese)

[20]刘健, 刘思峰, 吴顺祥. 基于优势关系的多属性决策对象排序研究[J]. 控制与决策, 2012, 27(4): 632-635.

Liu Jian, Liu Sifeng, Wu Shunxiang. Ranking research based on dominant relation for multiple-attribute decision making object[J]. Control and Decision, 2012, 27(4): 632-635. (in Chinese)

[21]Wang Y M, Luo Y. Integration of correlations with standard deviations for determining attribute weights in multiple attribute decision making[J]. Mathematical and Computer Modelling, 2010, 51(1-2): 1-12.

[22]Liesiö J. Measurable multiattribute value functions for portfolio decision analysis[J]. Decision Analysis, 2014, 11(1): 1-20.

[23]Fan Z P, Liu Y, Feng B. A method for stochastic multiple criteria decision making based on pairwise comparisons of alternatives with random evaluations[J]. European Journal of Operational Research, 2010, 207(2): 906-915.

[24]Csaszar F A, Eggers J P. Organizational decision making: An information aggregation view[J]. Management Science, 2013, 59(10): 2257-2277.

[25]刘健, 刘思峰, 周献中, 等. 基于相似关系的多属性决策问题研究[J]. 系统工程与电子技术， 2011, 33(5): 1069-1072.

Liu Jian, Liu Sifeng, Zhou Xianzhong, et al. Research on multiple-attribute decision making problems based on similarity relationship[J]. Systems Engineering and Electronics, 2011, 33(5): 1069-1072. (in Chinese)

[26]Skowron A. Extracting laws from decision tables: A rough set approach[J]. Computational Intelligence, 1995, 11(2): 371-388.

[27]Grbic T, Stajner-Papuga I, Strboja M. Approach to pseudo-integration of set-valued functions[J]. Information Sciences, 2010, 181(11): 2278-2292.

[28]Daniel K, Amos T. Prospect theory: An analysis of decision under risk[J]. Econometrica, 1979, 47(2): 263-292.

[29]Abdellaoui M, L’Haridon O, Paraschiv C. Experienced vs. described uncertainty: Do we need two prospect theory specifications?[J]. Management Science, 2011, 57(10): 1879-1895.

[30]Dimitris B, Vivek F F. On the efficiency-fairness trade-off[J]. Management Science, 2012, 58(12): 2234-2250.

[31]Amy R W, Mor A. Blind fair routing in large-scale service systems with heterogeneous customers and servers[J]. Operations Research, 2013, 61(1): 228-243.

[32]丁川, 王开弘, 冉戎. 基于公平偏好的营销渠道合作机制研究[J]. 管理科学学报, 2013, 16(8): 80-94.

Ding Chuan, Wang Kaihong, Ran Rong. Marketing channel coordination mechanism based on fairness preferences[J]. Journal of Management Sciences in China, 2013, 16(8): 80-94. (in Chinese)

[33]杜少甫, 朱贾昂, 高冬, 等. Nash讨价还价公平参考下的供应链优化决策[J]. 管理科学学报, 2013, 16(3): 68-72， 81.

Du Shaofu, Zhu Jiaang, Gao Dong, et al. Optimal decision-making for Nash bargaining fairness concerned newsvendor in two-level supply chain[J]. Journal of Management Sciences in China, 2013, 16(3): 68-72, 81. (in Chinese)

Dynamic decision process based on discrepancy of decision makers’risk preferences

LIUJian1,2,CHENJian2,LIAOWen-he3,MAYi-zhong1,LIUSi-feng4

1. School of Economics and Management, Nanjing University of Science and Technology, Nanjing 210094，China;2. School of Economics and Management, Tsinghua University, Beijing 100084, China;3. School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China;4. School of Economics and Management, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China

To study the decision process when decision makers have different risk preferences, a dynamic strategy, which classifies decision makers while approaching the solution, is proposed. First, effective attributes based on the similarity relationship of attribute values are extracted and weights are assigned to them objectively. Second, decision makers’ type of risk preferences (risk aversion, risk neutral, risk seeking) are converged into step by step according to the decision activities. According to the possibility and similarity of the interval numbers, the prospect theory models are established. Then, a suitable theoretical model is selected in the process of information aggregation and ranking according to decision makers’ risk preferences. Moreover, in order to maximize the fairness of the decision result, we propose a new information fusion algorithm is proposed when different types of decision makers exist at the same time. Finally, the new approach is validated via realistic examples.

discrepancy; risk preferences; dynamic strategy; fairness; decision process

① 2013-12-24；

2014-04-16.

国家自然科学基金青年基金资助项目 (71301075)； 江苏省自然科学基金青年基金资助项目(BK20130770)； 博士后国际交流计划派出项目(21040072)； 江苏省博士后科研资助计划项目(1501040A)； 南京理工大学“卓越计划紫金之星”资助项目； 南京理工大学青年教师科研基金资助项目(JGQN1401).

刘健(1982—)， 男， 山东淄博人， 博士后， 副教授. Email: jianlau7550@gmail.com

C936

A

1007-9807(2016)04-0001-15