谐波齿轮传动的齿形设计
庄剑毅,梁桂转
(广州市昊志机电股份有限公司,广东广州510000)
谐波齿轮传动的齿形设计
庄剑毅,梁桂转
(广州市昊志机电股份有限公司,广东广州510000)
基于曲线映射理论,阐述谐波齿轮传动非干涉且大范围啮合齿形的设计方法。先根据柔轮中线上点的运动轨迹,确定近似齿形;然后考虑柔轮齿倾斜和运动轨迹改变的情况,对近似齿形进行适当修正,得到最终齿形。
谐波齿轮;齿形设计;曲线映射
谐波减速器具有体积小、传动比大、效率高、精度高等特点,并且作为核心零部件而广泛应用于工业机器人和精密定位系统中。为保证卓越的传动性能,谐波齿轮在角度传动精度、强度、刚度等方面具有极高要求,而要实现这些高性能要求,齿形设计至关重要。本文阐述文献[1]所披露的一种应用于谐波齿轮传动的非干涉且大范围啮合齿形的设计方法。
1 曲线映射理论
如图1所示,柔轮中线上点的运动轨迹为曲线a0b0,c0是a0b0上的任意一点。刚轮的上齿面曲线a1b1由a0b0进行几何映射(即比例缩放)得到,缩放比例为0.5.a1b1以a1为中心旋转180°,即为柔轮上齿面曲线a2b2.同时,c0在a1b1与a2b2上的对应几何映射点分别为c1与c2.
当中线上的点由点a0运动至点c0,柔轮上齿面a2c2b2则运动至a2'c2'b2'.由于曲线几何映射的特殊性质,柔轮上齿面曲线的点c2'与刚轮上齿面曲线的点c1相互重合并且相切。这样,柔轮在整个运动过程中均与刚轮保持接触而又不干涉,齿轮的啮合性能进而得以大幅度提升。

图1 曲线映射原理示意图
2 近似齿形的设计
当谐波齿轮装置采用基于余弦凸轮的波发生器,柔轮中线上点的运动规律如下[2]:

其中,ω为径向位移,υ为周向位移,m为中线模数,θ为柔轮非变形端之转角。
假设柔轮、刚轮均为齿条,则柔轮中线上点相对刚轮的运动轨迹如下:
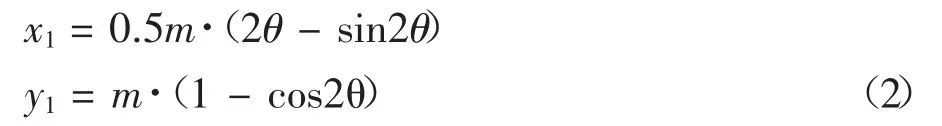
根据曲线几何映射理论,并经适当的坐标转换,便得到近似设计的上齿面齿形曲线如下:
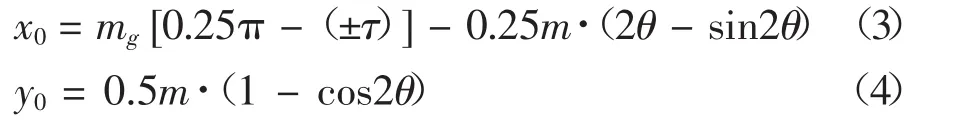
其中,mg为齿轮模数,τ为齿厚变化系数。
但是,实际中柔轮与刚轮均为圆柱齿轮而不是齿条,柔轮中线上点相对刚轮的运动轨迹与假设的有所变化,同时,柔轮齿在啮合过程中存在齿廓倾斜现象。因此,还需对近似设计的上齿面齿形曲线进行修正。
3 齿形修正
齿形的修正包括柔轮齿倾斜的修正与运动轨迹改变的修正。在修正齿形之前,需清楚柔轮与刚轮之间的坐标关系。
如图2所示,设有一固定坐标系OXY与波发生器固联,Y轴与波发生器长轴相重合,原点O位于波发生器中心上。两动坐标系OFXFYF和OCXCYC分别与柔轮和刚轮固联。YF轴与柔轮齿的对称轴线相重合,原点OF位于柔轮中线上,而YC轴与刚轮齿槽的对称轴线相重合,原点OC位于刚轮的回转中心上。
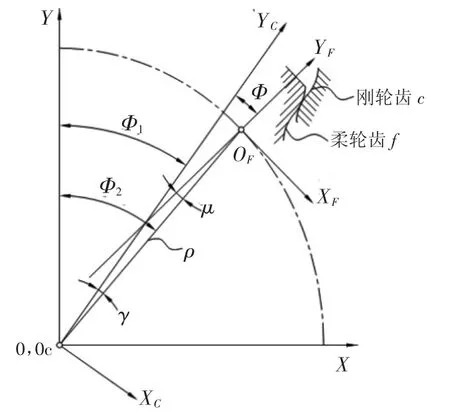
图2 柔轮齿与刚轮齿的坐标关系
当柔轮非变形端旋转θ角,得到以下坐标关系等式[3]:
YC轴相对Y轴的转角为:Φ1=(ZF/ZC)·θ
矢径OOF(记为ρ)相对Y轴的转角为:
Φ2=θ-0.5·m·sin2θ/rn
YF轴相对矢径ρ的转角为:
μ=arctan{2·m·sin2θ/(rn+ω)}
YF轴相对YC轴的转角,即柔轮齿的倾斜角为:
Φ=γ+μ
其中,ZF为柔轮齿数,ZC为刚轮齿数,rn为变形前柔轮中线的半径,γ=Φ2-Φ1.
设柔轮齿倾斜修正项为g1,则有[4]:
g1=h·Φ
h=0.5·t+mg·(ha*+c*)+f
f=0.5·m·[1-cos2θ]-0.5·tanθ
·{mg·[0.25π-(±τ)]-0.25m·(2θ-sin2θ)}
其中,t为柔轮的轮缘厚度,ha*为齿顶高系数,c*为顶隙系数。
设运动轨迹改变的修正项为g2,则有[4]:g2={0.5·m·[2θ-sin2θ]-xN}
+0.5·tanθ·{yN-m[1-cos2θ]}xN=(rn+m·cos2θ)·sinγ
yN=(rn+m)-(rn+m·cos2θ)·cosγ
4 最终齿形
根据修正项g1与g2对近似设计的上齿面齿形曲线方程(3)和(4)进行修正便得到最终的上齿面齿形曲线,曲线方程如下:
x=mg[0.25π-(±τ)]
-0.25m·(2θ-sin2θ)-0.5(g1-g2)y=0.5m·(1-cos2θ)
下齿面齿形曲线则在保证不产生干涉的前提下,可根据工艺便利性,选用任意的曲线。
5 齿形验证
当取m=0.5,ZF=200,Zc=202,t=1,ha*=0.8,c*=0.25,τ=0.2,根据上述设计方法与相关曲线方程式,得到的柔轮齿廓与刚轮齿廓分别为图3所示的曲线f与c.同时,图3展示了柔轮齿啮入刚轮齿的过程,整个啮合过程柔轮齿均与刚轮齿保持接触并且没有干涉。也就是说,采用本文所设计齿形能够在不产生干涉的前提下获得大范围啮合。
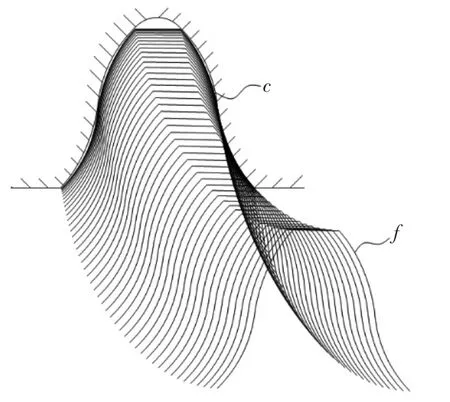
图3 柔轮齿与刚轮齿运动啮合示意图
因此,采用本文齿形的谐波齿轮在工作时,同时啮合的齿数非常多,可以多达总齿数的30%,相比之下,传统渐开线齿形的谐波齿轮在受力的情况下,同时啮合的齿数也不会超过总齿数的15%.同时啮合齿数的增加,能够直接大幅度提升谐波齿轮在刚性、传动精度、输出转矩等各方面的性能,提升幅度在30%以上。
6 结束语
谐波齿轮非干涉且大范围啮合齿形的设计方法是基于曲线映射理论的;先根据柔轮中线上点的运动轨迹,确定近似齿形;然后考虑柔轮齿倾斜和运动轨迹改变的情况,对近似齿形进行适当修正,得到最终齿形。该齿形增加了同时啮合的齿数,进而大幅度提升谐波齿轮在刚性、传动精度、输出转矩等各方面的性能。另外,本文所述为理想情况下的齿形设计,实际中齿轮制造必然会存在误差,因此,还需根据实际的加工精度水平对齿形做进一步修正与优化。
[1]Shoichi Ishikawa,Kanagawa-ken.Strain Wave Gearing Having a Non-Interfering Wide Mesh Range Tooth Profile: US:5918508[P].1999-06-06.
[2]M.H.伊万诺夫,沈允文,李克美.谐波齿轮传动[M].北京:国防工业出版社,1987:30-31.
[3]沈允文,叶庆泰.谐波齿轮传动的理论和设计[M].北京:机械工业出版社,1985:68-71.
[4]汤秀清,庄剑毅.一种采用非干涉且大范围啮合齿廓的谐波齿轮装置:中国:CN104819267A[P].2015-08-05.
Tooth Profile Design of Harmonic Gear Drive
ZUANG Jian-yi,LIANG Gui-zhuan
(Guangzhou Hao Chi Electrical Limited by Share Ltd.,Guangzhou Guangdong 510000,China)
Base on curve mapping theory,a design method was presented for harmonic gear having a noninterfering wide range tooth profile.According to themovement locus of the tooth of flexspline,approximate tooth profile was achieved.Then taking account of tooth inclination and change in tooth movement locus,approximate tooth profile was corrected and final tooth profile was obtained.
harmonic gear;tooth profile design;curvemapping
TH132.43
A
1672-545X(2016)05-0075-02
2016-02-12
庄剑毅(1985-),男,广东广州人,研究生,工程师,研究方向:机器人用精密减速器设计。

