线控转向驾驶员模型反馈系数优化

杨胜培

（湖南师范大学工程与设计学院，湖南长沙410083）

线控转向驾驶员模型反馈系数优化

杨胜培

（湖南师范大学工程与设计学院，湖南长沙410083）

线控转向系统可以根据车况灵活改变角传动比以提高汽车的操纵稳定性。基于单点预描最优曲率模型，利用车辆转向时的Ackerman几何关系和转向时的稳态横摆角速度与车辆实际横摆角速度之差和理想侧向加速度与车辆实际侧向加速度之差对车辆转向盘转角进行补偿，建立驾驶员转向模型。在建立整车动力学模型和驾驶员模型的基础上，从人--车闭环系统角度出发，采用汽车操纵稳定性综合评价体系中的轨迹跟踪误差总方差、方向误差总方差、车辆侧向加速度总方差、转向盘忙碌程度总方差和侧向力系数总方差所构成的综合评价指标为适应度目标函数与具有全局优化能力的粒子群优化算法相结合对参数进行优化，并将其与参数优化前结果进行对比。试验结果证明了粒子群优化算法的有效性，该算法能够改善操纵稳定性，使优化后的结果能更精确地控制车辆跟随预定的路径。

驾驶员模型；侧向加速度；横摆角速度；粒子群优化

线控转向（SBW）系统取消了方向盘与转向器之间的机械连接，采用线控技术控制汽车的转向运动。由于转向传动比可以通过软件自由设定，因而使汽车各方面的性能都得到较大提高［1-3］。

由于车辆行驶时，需要根据车辆当前的行驶状态和路面情况确定合理的前轮转角。本文在郭孔辉院士提出的“预瞄—跟随”驾驶员建模理论的基础上，引入车辆实际侧向加速度与理想侧向加速度之差和实际横摆角速度与稳态横摆角速度之差进行反馈，据此建立驾驶员模型，对转向盘转角进行修正，从而控制前轮转角。

本文根据预期道路的信息，通过引入汽车行驶状态反馈，补偿施加到汽车上的转向盘转角，采用粒子群优化算法对驾驶员模型的反馈系数进行优化并与优化前的模型进行了对比。

1　线控转向系统的转动比

线控转向系统中转向轮与方向盘之间不再采用传统的机械连接，因此其传动比不再是固定的传动比。线控转向系统的转动比可根据转速设置理想的转动比。线控前轮转向系统的理想传动比为［4］：

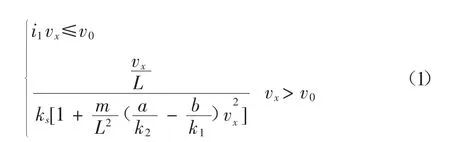
式中，k1、k2分别为前后轮侧偏刚度；m为整车质量；vx为车辆前进速度；a、b分别为前后轮到车身质心的距离；L为轴距，L=a+b.对于一般驾驶人员，车辆理想转向特性的横摆角速度增益即转向灵敏度为0.12 1/s～0.37 1/s［5］，因此，本文在仿真中转向灵敏度的取值范围取0.12～0.37.

2　驾驶员模型

采用单点预瞄最优加速度（最优曲率）建立驾驶员模型，驾驶员模型最小误差的确定原则是：汽车的运动轨迹尽可能与预期的轨迹相一致。根据“预瞄—跟随”驾驶员建模理论［6］，驾驶员获取道路前方信息的方法是通过“预瞄”。假设汽车当前的实际侧向位移为y（t），期望的侧向位移为f（t），而驾驶员预瞄过程的时间为T.驾驶员对当前转向盘操作的期望是经过预瞄时间T后，车辆的实际侧向位移y（t+T）尽可能逼近汽车期望的侧向位移f（t+T）.

图1是单点预瞄运动分析示意图：t时刻车辆的侧向位移为y（t），侧向速度为vy，假设在当前时刻汽车以理想的侧向加速度在侧向做匀加速运动，经过时间T之后，车辆可以到达期望轨迹，则

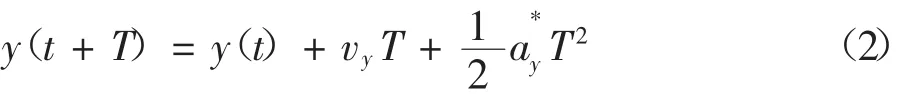
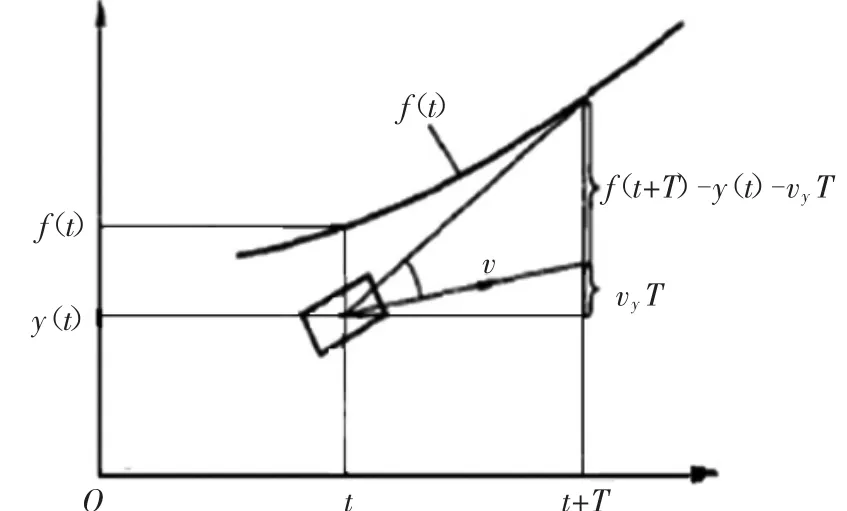
图1　单点预瞄运动分析示意图

根据“最小误差原则”，驾驶员总是希望汽车在走过距离d（经预瞄时间T）后，其横向位置与该对应位置y（t+T）处的预期轨道坐标f（t+T）相一致。因此，由式（2）可得到最优侧向加速度即理想侧向加速度为

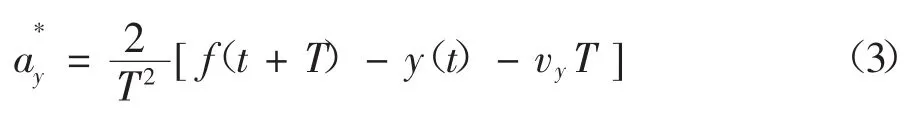
当车速不高且路径方向角不大时最优侧向加速度、方向盘转角可由式（4）、（5）决定：

由（3）、（4）式，可得到转向盘转角为：

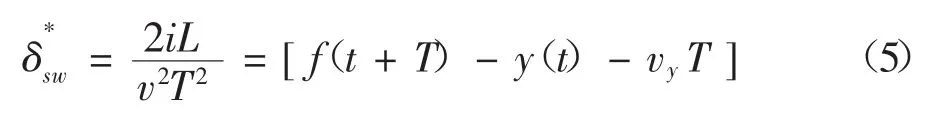
考虑驾驶员的生理限制以及车辆的使用状态，提出了图2所示的基于车辆状态（即车辆理想侧向加速度与实际侧向加速度之差以及车辆稳态横摆角速度与实际横摆角速度之差）反馈的驾驶员模型。

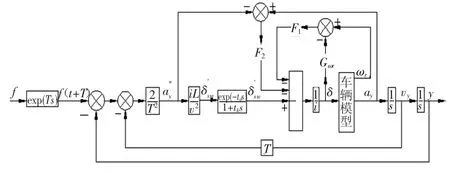
图2　基于状态反馈的驾驶员模型

驾驶员的生理限制主要有神经反应滞后和动作反应滞后。神经反应滞后可用传递函数exp（-tds）来表示，td为神经反应滞后时间。动作反应滞后可用传递函数为1/（1+ths）表示，th为动作反应滞后的时间常数，因此，考虑驾驶员的生理因素后的转向盘转角为.由于驾驶员的反应滞后以及汽车复杂的行驶工况等因素的影响，使用δ'sw进行方向控制时实际产生的横摆角速度以及汽车侧向加速度的值不同于理想的稳态横摆角速度以及汽车侧向加速度。为此提出了采用实际侧向加速度与理想侧向加速度的差值和实际横摆角速度与稳态横摆角速度的差值进行反馈的方式对根据驾驶员模型计算出的前轮转角进行修正，得到修正后的前轮转角为

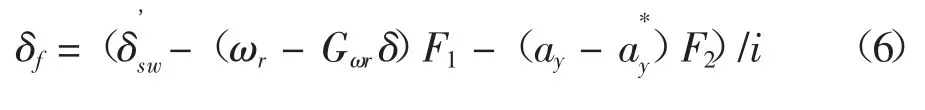
3　前轮转向车辆运动方程

假设汽车在水平路面上匀速行驶，将车辆简化成考虑质心处侧偏角β以及横摆角速度ωr的线性动力学模型，车辆模型如图3所示。2自由度侧向和横摆动力学方程如下：

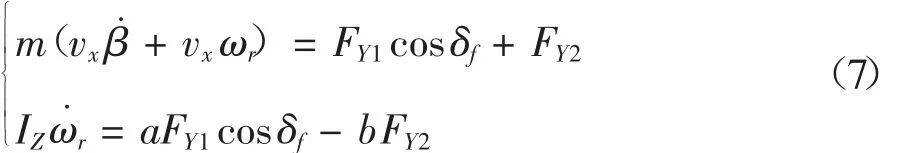
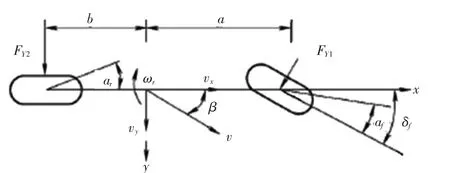
图3　2自由度车辆动力学模型

式中，FY1为前轮侧向力；FY2为后轮侧向力；vy为侧向速度；IZ为车辆绕Z轴的转动惯量；δf为前轮转向角。β和ωr分别为车辆质心侧偏角和横摆角速度，其它字母的含义与前同。

其中:侧向加速度ay=vx（ωr+β.）

将β用vy/vx替代后消去vy可得汽车转向增益为:

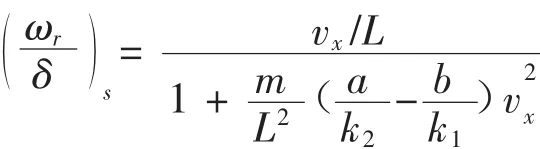
所以可得到稳态下的横摆角速度为:

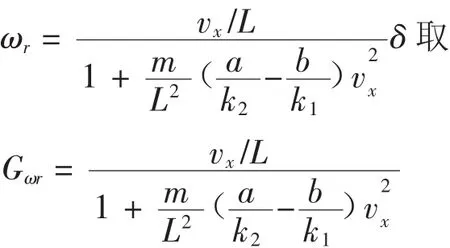
4　评价函数

考虑车辆的操纵性及稳定性能，本文从轨道跟随误差总方差、侧向加速度总方差、方向误差总方差、转向盘角速度总方差、车辆侧滑性等方面评价车辆的稳定性控制策略。对这些性能指标进行加权组合得到反映汽车动态性能和转向系统性能的综合评价指标，安全性综合评价指标为：

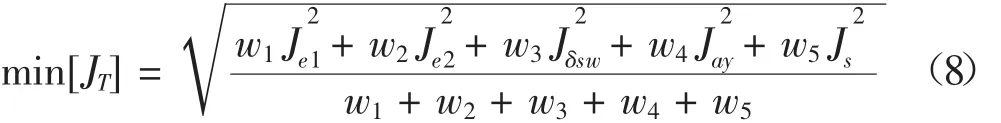
式中:w1、w2、w3、w4、w5为各单项指标的权值，本文在计算中采用优化算法确定各权重值。Je1为轨迹跟踪误差指标；Je2为方向误差指标；Jδsw为驾驶员忙碌程度指标；Jay为侧向加速度总方差；Js为侧向力系数总方差。

5　基于粒子群理论的参数优化

5.1粒子群理论

粒子群优化算法是由KENNEDY等［7-8］源于对鸟群觅食行为的模拟研究，于1995年提出的一种新的基于群体智能的全局优化算法［9-10］。

设粒子群体规模为N，每个粒子在D维空间中的坐标位置表示为xi=（xi1，xi2，…，xid，…，xiD），微粒的速度定义为迭代中微粒每次移动的距离，用vi=（vi1，vi2，…，xiD）表示，于是，微粒i（i=1，2，…，N）在第d（d=1，2，…，D）维子空间中的飞行速度vid根据式（9）进行调整

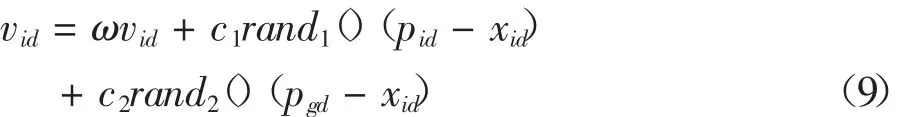
其中，vid∈［vmin，vmax］

式中，pgd表示整个微粒群的历史最优位置；pid表示当前微粒的历史最优位置；ω是惯性权重，c1，c2是加速常数。对微粒的速度vi进行了最大速度、最小速度限制，如果当前对微粒的加速将导致它在某维的速度分量vid超过该维的最大速度限制vmax，则该维的速度被限制为最大速度vmax；如果超过了最小速度vmin，则该维的最小速度将限制为最小速度vmin.根据式（10）调整微粒的位置

其中，xid∈［xmin，xmax］

研究表明，惯性系数较大时对全局搜索有利，较小时对局部收敛有利。故开始搜索时，设置的惯性系数较大，然后让其线性减小，逐步提高其局部搜索能力，其线性减小的公式为

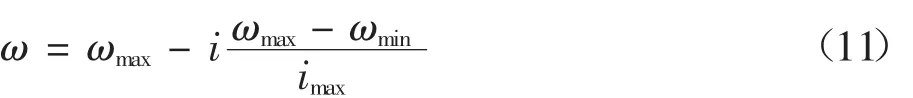
式中，i为当前迭代次数，imax是总的迭代次数，ωmax为最大加权系数，ωmin为最小加权系数。

根据式（11）可知，随着迭代次数的不断增加，惯性系数ω从ωmax线性减小到ωmin，目标函数值逐步接近最优值。本文中适应度函数为评价函数的计算值，种群粒子数为20，每个粒子的维数为2，算法迭代进化次数为500.

5.2粒子群优化

应用粒子群理论对参数进行优化的步骤如下：（1）初始化参数，随机生成粒子群的位置和速度。（2）对每个粒子的适应值进行计算。

（3）计算每个粒子的适应值并与其所经历过的最好位置的适应值进行比较，若较好，则将其作为当前的最好适应值。

（4）计算每个粒子的适应值并与全局所经历过的最好位置的适应值进行比较，若较好，则将其作为当前的全局最好适应值。

（5）根据方程（9）、（10），优化粒子的速度和位置。

（6）判断粒子群算法是否达到最大迭代次数，或者判断全局最优粒子的适应度值是否满足收敛条件，满足则终止循环；如果不满足，则返回（2），进入下一次迭代循环。

5.3仿真及控制参数优化的实现

为使驾驶员模型实现最优的驾驶，需要对驾驶员模型的反馈系数进行优化。本文采用粒子群优化算法对反馈参数和各项指标权值进行优化计算。以本文推导的汽车安全性综合评价指标式（8）为目标函数，采用描述汽车操纵稳定性的双移线试验工况进行仿真试验。在算法实现过程中，驾驶员的特性参数选取为：预瞄时间T=1.0 s，动作反应滞后时间［11］th=0.1 s，神经反应滞后时间td=0.4 s.同时假设车辆在该路段运行速度恒定，设定仿真时间160 s.仿真时所用的车辆模型参数为：M=3 018 kg，Iz=10 437 kg·m2，a=1.84 m，b=1.88 m，k1=-46 328 N/rad，k2=-766 90 N/rad.

双移线试验工况如图4所示，图4中所示试验工况一是采用粒子群算法优化参数后得到的曲线，另外一条是粒子群算法优化前的曲线。

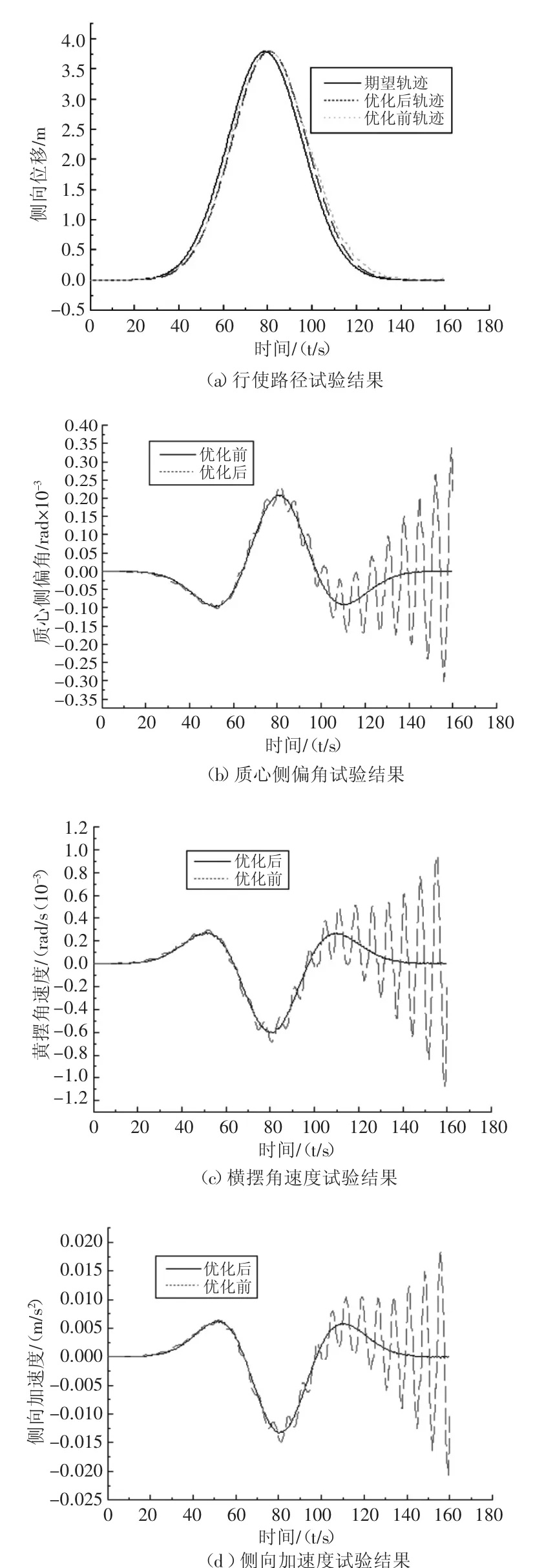
图4　双移线试验结果（80km/h）

从图4（a）-（d）可以看出，优化后的车辆质心侧偏角、横摆角速度、侧向加速度波动幅度较小，而优化前则波动幅度较大，这是由于质心侧偏角、横摆角速度、侧向加速度的单位分别精确到0.000 05 rad，0.000 02 rad/s，0.005m/s2，在图上放大了波动的效果。优化后的车辆行驶轨迹更接近车辆期望行驶轨迹。从表1可以看出优化前车辆的安全性综合评价指标比优化后的值大，表明优化后车辆的稳定性能得到了改善。

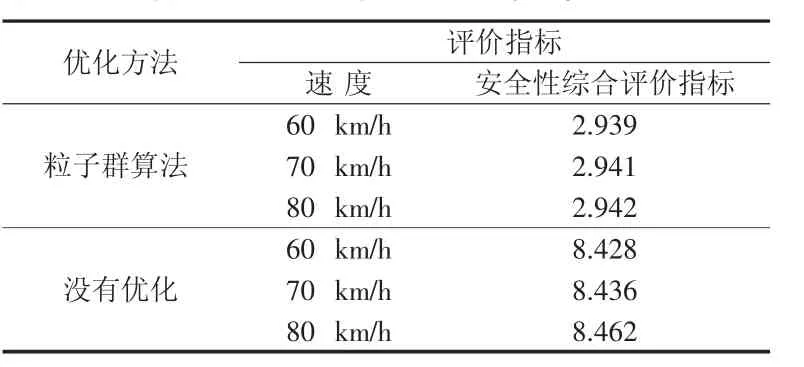
表1　2种控制方法的安全性综合评价指标对比

6　结束语

（1）本文提出的仿真模型参数数量少，物理意义清晰，模型可以直接计算汽车行驶轨迹的侧向位移、侧向加速度，仿真结果表明了模型的有效性。

（2）随着车速的变化，经过粒子群优化算法计算的车辆安全性综合评价指标比优化前计算的车辆安全性综合评价指标要小，表明在车辆速度相同的情况下，优化后车辆行驶的稳定性得到了改善。

［1］Onoda Y.Onuma Y.Goto T，et al.Design concept and advan tages of steer-by-wire system［C］.SAE Paper 2008-01-0493.

［2］Yao et al.System and method of controlling vehicle steer-by -wire systems［M］.United states:US 6，694，239 B1，2004.

［3］Shoji Asai.Development of Steer-by-Wire System with force feedback using a disturbance observer［R］.SAE paper，2004 -01-1100.

［4］于蕾艳，林逸，施国标.线控转向系统的角传动比研究［J］.农业机械学报，2007，38（8）:190-192.

［5］徐正会，张元鸿.车辆可变齿轮比转向系统之创新设计.台湾第19届机械工程研讨会论文［C］.2002.

［6］郭孔辉.汽车操纵动力学原理［M］.南京：江苏科学技术出版社，2011.

［7］KENNEDY J，EBERHART R C.Particle swarm optimization［C/CD］//Proc.of IEEE International Conference on Neural Networks，1995.

［8］EBERHART R C，SHI Y.Particle swarm optimization：developments，applications and resources［C］.Proc.Congress on Evolutionary Computation，Soul，South Korea.Piscataway，NJ：IEEE，2001：81-86.

［9］张涛，程海刚，张玥杰，等.基于MTO-MTS的钢厂合同计划方法［J］.系统工程理论与实践，2008，17（11）：85-93.

［10］ZHAO Yuxin，ZU Wei，ZENG Haitao.A modified particle swarm optimization via particle visual modeling analysis［J］. Computers&Mathematics with Applications，2009，57（6）：2022-2029.

［11］Andrzej Ren‘ski.Identification of driver model parameters［J］.International JournalofOccupational Safety and Ergonomics，2001，17（1）:79-92.

Optim ization of The Feedback Coefficient AboutDriver ModelBased On Steer-by-W ire

YANG Sheng-pei
（College of Engineering and Design，Hunan Normal University，Changsha Hunan 410081，China）

Steer-by-Wire system can change steering ratio according to vehicle state to improve vehicle handling and stability.Based on single point preview optimal curvaturemodel，a driver steeringmodelwas built，Where the target steering angle is compensated according to the Ackerman geometry of steering and the feedback steering angle of the yaw-rate under steady steering minus the vehicle actual yaw-rate and the ideal lateral acceleration minus the vehicle actual lateral acceleration.On the basis of the vehicle dynamics and the driver steeringmodel，The optimization was based on driver-vehicle closed-loop，and adopted comprehensive evaluation indexes of vehicle handling and stability as fitness function，Which include lateral trace error total variance，direction error total variance，vehicle lateral acceleration error total variance，driver steering load and lateral force coefficients error total variance.Particle swarm theory，with global optimization capability was applied to optimize the result of driver-model.Compared with the results before particle swarm，validity of particle swarm theory applied in drivermodelwas testified.Simulation results after optimization showed that the vehicle in themodel can follow the preset pathswell，thereby improve vehicle handling stability.

drivermodel；lateral acceleration；yaw-rate；particle swarm optimization

U461

A

1672-545X（2016）05-0011-05

2016-02-19

湖南省教育厅科学研究项目（15C0821）

杨胜培（1968-），男，湖南人，博士，研究方向：数字化设计，制造以及智能优化。