Optinum Design of Electro-Hydrostatic Actuator Controller Based on Adaptive Genetic Algorithm*

XIE Peng，ZHANG HONGmei（College of Science，Air Force Engineering University，Xi’an 710038，China）



Optinum Design of Electro-Hydrostatic Actuator Controller Based on Adaptive Genetic Algorithm*

XIE Peng*，ZHANG HONGmei
（College of Science，Air Force Engineering University，Xi’an 710038，China）

Since Electro-hydrostatic Actuator dynamic response is difficult to meet the requirements of flight control system，this paper designed a feedback control scheme of position，speed and current closed-loop and proposed an op⁃timization method of controlller parameters based on Adaptive Genetic Algorithm.Firstlly，system model was estab⁃lished，integral separation was added to speed and current PI regulators to avoid saturation.Secondly，considering the premature convergence and low efficiency of Standard Genetic Algorithm，adaptively changed crossover and muta⁃tion probability were adopted，real-coded scheme with higher accuracy was used，appropriately weighted constaints were introduced into ITAE.Finally，through parameter tramsfer on MATALAB，algorithm was combined with Simu⁃link model for PID setting，made rise time，overshoot and accommodation time separetely descrease to 0.083 s，4.76% and 0.318 s.The experimental results show that AGA can efficiency improve EHA rapidity，accuracy and stability.

electro-hydrostatic actuator；adaptive genetic algorithm；real-coded scheme；parameter transfer；opti⁃mum design

EHA作为支撑功率电传发展的关键技术之一，对于减轻飞机起飞重量、提高液压系统可维修性具有重要作用［1］，国内关于这方面研究起步不久，目前还处于原理论证阶段，由于机、电、液一体化系统具有复杂非线性与不确定性，并且直接对承载着交变动载荷的舵面操作，因此设计出满足一定性能指标的控制器成为难点之一［2］。经典PID控制策略最早发展起来，实际工程中90%以上回路仍然应用着［3］，具有结构简单、易于实现等特点，同时不受被控对象特性变化影响，使系统保持了较高快速性、精确度与鲁棒性，适用于机载作动平台，但程序繁琐的控制参数整定一直困扰着技术人员［4］。传统PID参数整定方法费事费力，大多在经验公式或统计数据指导下试凑得到，例如Ziegler-Nichols阶跃响应法、临界振荡法、衰减曲线法［5］，利用这种带有一定主观性方法很难使多变量、非线性、强耦合系统达到理想的控制效果。

GA只依赖于适应度函数而不限制目标函数连续或可导，即使在被控对象模型不确定情况下，也能根据输出结果在全局范围内高效启发式搜索［6］。本文结合EHA系统组成，逐级设计PID位置调节器、PI转速与电流调节器，利用交叉与变异概率自适应变化的GA整定控制参数，采取实数编码与最优保存策略改进SGA，通过MATLAB/Simulink编程计算与仿真分析，验证AGA对于EHA控制系统优化的有效性。

1　EHA系统建模

EHA结构组成如图1所示［7］。无刷直流电动机1最高转速为12 000 r/min；双向柱塞泵2排量取为定值1 mL/r；储能器4一是通过单向阀3（1）返回泵壳体回油，二是通过单向阀3（1）、3（2）补充油液泄漏，保持系统最低压力；过滤器5以去除管道中杂质，达到泵稳定工作清洁度；安全阀6当作动筒突然受到非正常外力时，排油以卸除缸口过高压力；阻尼旁通阀7位于双腔液压缸8之间，系统发生故障时打开，将油液返到吸油口。

正常工作时，DSP控制器接收飞行控制计算机指令并根据传感器检测到位移、电流、转速及压差综合生成控制信号，功率驱动电路将电压变换为电流控制电动机转速与转向，泵被带动产生压力油送至液压缸，活塞在压力作用下从而使作动筒产生相应位移。电能在传输中经历了液压能到动能转变，形成闭环控制系统完成对舵面的操作。

1.1电动机数学模型

忽略逆变器内部的动态过程，通过传递函数来表达方波电动机电枢电压Vc与DSP控制信号电压Uc之间的关系：

电动机主回路电压平衡方程为：

假设电动机与泵直接相连，则转矩平衡方程为：

联立（1）～（3）式并不考虑负载转矩，则电动机转速ω与电枢电压之间的传递函数为：

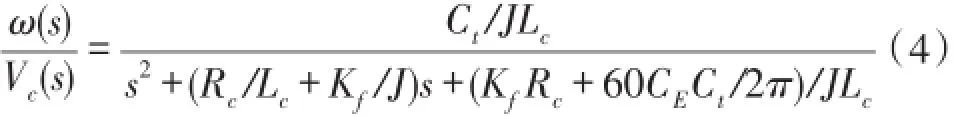
式中：Ks为电压放大系数；Ts为晶闸管时间常数；E=CEn为反电动势；CE为反电势系数；n=60ω/2π为转子线速度；Rc为电枢绕组；Lc为电枢电感；Ic为电枢电流；Tt=CtIc为电磁转矩；Ct为电磁转矩系数；J=Jm+Jp，Jm、Jp分别为电动机与泵转动惯量；Kf=Kvisc+Kfric，Kvisc、Kfric分别为电动机粘度与摩擦系数；Dp=D 2π，D为泵排量；Pa、Pb为分别为泵出入口压力。

1.2液压部分数学模型

忽略储能器补油动态过程，泵出入流量Qa、Qb分别为：

液压缸出入流量Q1、Q2分别为：

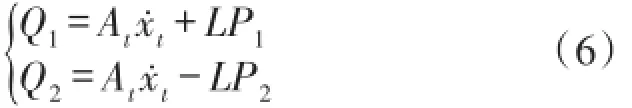
假设泵与液压缸连接管道为刚性，则流量连续性方程为：

作动筒力平衡方程为：

联立式（5）～式（8）并不考虑负载力，则作动筒位移xt与电动机转速之间的传递函数为：

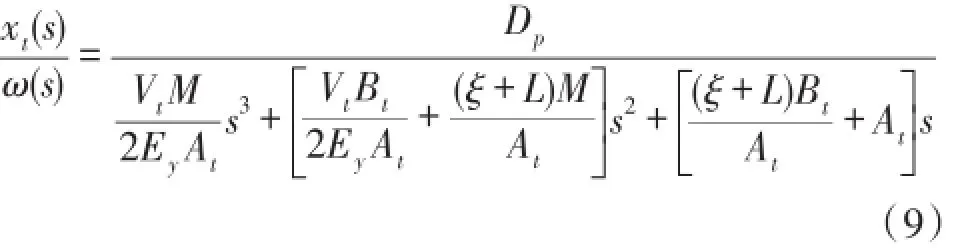
式中：ξ为泵内部泄漏系数；Le为泵和液压缸外部泄漏系数；Pcase为储能器口压力；At为活塞受力面积；P1、P2分别为两容腔压力；Vt为管道和液压缸的平均容积；Ey为油液等效体积弹性模量；F=AtPL为活塞驱动力；PL=P1-P2为负载压力；M为负载等效到作动筒上的总质量；Bt为负载与作动筒的粘性阻尼系数；FL为负载力。

2　EHA控制器设计

2.1电动机调速系统

无刷直流电动机在电功率转换为液压功率从而驱动活塞做功过程中起关键作用，直接影响着整个EHA工作性能。相关文献资料与实践经验表明［8］，带限幅输出的双闭环负反馈串级连接调速系统具有更好的动、静态特性，其中转速环作为主PI调节器使电动机转速动态速降小、恢复时间短，保证系统响应快速性；电流环作为副调节器使电枢电流线性受控，保证系统工作稳定性。

转速调节器只有在系统发生超调时才能退出饱和，这里引入积分分离项，当被控值与给定值偏差大于预设值时去掉积分环节，不再限制PWM变换器输出电压。实际工作中电刷换向和PWM调制将造成电枢电流脉动，为抑制其谐波分量，在转速与电流反馈回路上增加一阶惯性滤波环节，并在调节器给定端设置同样时间常数滤波环节以平衡对系统造成的延迟，电动机调速系统在Simulink中的实现如图2所示。

图2　电动机调速系统在Simulink中的实现

2.2EHA仿真平台

图3　EHA仿真平台

EHA最终要完成对作动筒位移精确控制，并且满足机载设备快速性与稳定性的要求。对此位置环采用PID调节器，设计指标为作动筒位移能跟随给定信号变化，同时系统在稳态时能消除静差，在动态过程中能克服负载扰动，确保正常运行可靠性。综上将位置环、转速环及电流环采取串级连接方式，形成三闭环的控制系统。由于MATALAB语言编写简单，数据传递方便，因此在其配置的Simulink环境下搭建整个系统的可视化仿真平台，如图3所示，为下一步利用AGA对调节器参数进行整定做好准备。

3　基于AGA的PID参数优化

GA通过模拟自然界生物进化过程与规律来搜索问题最优解［9］，从一个代表问题可能解集并经过基因编码的初始种群出发，依据“优胜劣汰、适者生存”的原则逐代演化（在数学上表现为迭代运算），通过适应度函数对每代种群中个体进行评价，同时借助遗传算子进行选择、交叉及变异以产生比前代更加满足问题需求的后代，如此循环达到算法终止条件，最后将末代种群中最优个体解码作为问题的最优解。

3.1AGA主要思想

在参数的优化过程中，交叉概率Pc与变异概率Pm的选取至关重要，越大的Pc与Pm能越快地产生新个体，但过大时启发搜索会变成随机搜索，过小时搜索会变得迟钝、甚至停滞，SGA一般取0.60～0.95与0.005～0.010之间的定值，根据人为经验和问题本身而主观设定，很难得到理想的最优解。为了防止早熟收敛并保证搜索效率，AGA中Pc与Pm随种群适应度值的变化而变化［10］，在个体适应度值低于种群平均适应度值时，采用较大的Pc与Pm，反之采用较小的Pc与Pm，计算公式如下：

式中，Pc1=0.6，Pc2=0.9；Pm1=0.001，Pm2=0.01；favg为种群平均适应度值；fmax为种群最大适应度值；f′为要交叉个体中较大适应度值；f要变异个体适应度值。

此外，利用实数编码的GA不用对二进制染色体每一位进行操作［11］，提高了全局搜索能力并降低了复杂性，有利于防止陷入局部最优，具有更高的计算精度和运行效率，实数编码的AGA参数整定流程如图4所示。

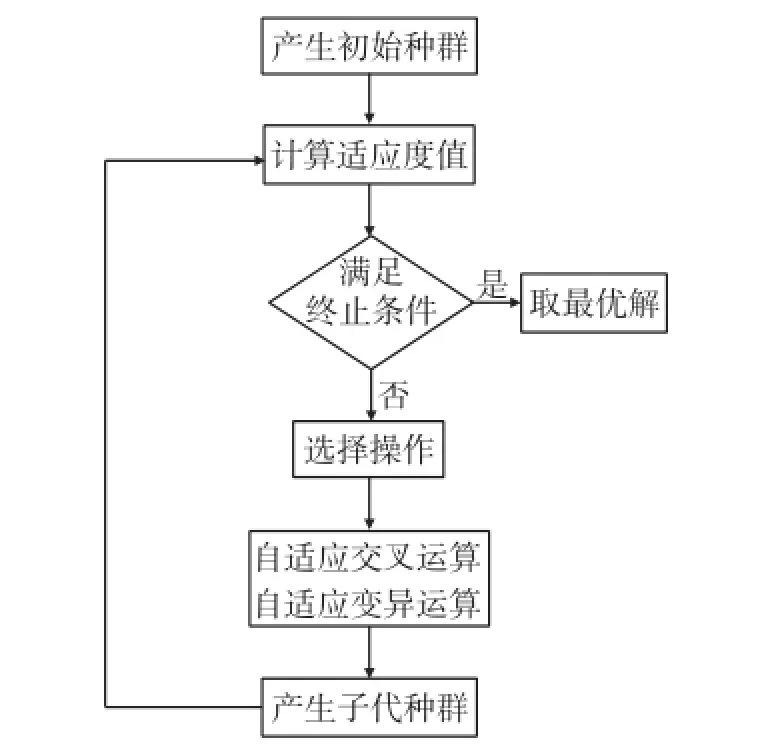
图4　实数编码的AGA参数整定流程

3.2EHA控制器参数优化步骤

3.2.1问题描述

针对第二部分设计的两个PI和一个PID调节器，确定待优化参数为Kdp、Kdi、Kdd、Kni、Knp、Kip、Kii，假设分别对应的基因位为p1、p2、p3、p4、p5、 p6、p7，那么EHA控制参数优化问题就可以描述为找个这样的一组解使系统的性能达到最优。

3.2.2参数初始化

为避免在不稳定解上浪费搜索时间，先用Ziegler-Nichols方法得到一组参数，然后取其0.7倍～1.3倍的范围作为解空间，设定初始种群规模为30、最大迭代代数为100。

3.2.3适应度函数选取

依据对EHA控制器的性能要求，选用ITAE型性能指标并加入调节器输出u和上升时间tu作为约束条件，以防止控制能量过大而导致系统不稳定，又具有一定的动态品质，同时如果产生超调时，将超调量作为惩罚项，则目标函数为：

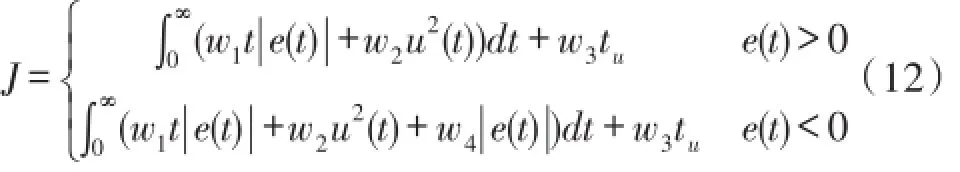
式中：e（t）为给定值与实际值的偏差，参考文献［12］，取w1=0.9、w2=0.02、w3=0.001、w4=100。

定义群体X中第i个个体的适应值为f（Xi）= 1/（1+J）。

3.2.4遗传算子设计

①选择算子

选择算子负责把握进化方向，当代个体Xi被选中复制到后代的概率为：

为使当代最优个体不被交叉与变异操作所破坏，需采用最优保存策略，直接替换后代最差个体。

②交叉算子

交叉算子在保持优良个Jp/（kg·m2）体特征的同时增加群体的多样性Ey/（N/m2），以式（11）计算的交叉概率Pc取个体XA与XB并随机产生一个交叉系数α，新生成的个体为：

③变异算子

变异算子使算法具有局部搜索能力，防止停滞不前，以式（12）计算的变异概率Pm取个体Xi=［p1，p2，…，pk，…，pN］并在范围内随机产生一个变异系数Δ（g，y），要求趋近于1的概率随着代数g的增加而增加，随机产生的变异点pk变异为：

3.2.5参数组传递

EHA控制系统复杂性决定了无法用传递函数对其进行准确地描述，在利用AGA对控制器参数优化时，需要通过MATLAB中M文件与Simulink模块之间接口实现跨空间的参数组传递。M文件自动修改调节器中的参数并调用Simulink模块在该参数下进行仿真，fitness.m根据系统误差、调节器输出、超调量等信息计算得到对应的适应度值，随后算法程序继续对参数进行优化，如此反复交替的进行使仿真与优化有机地结合起来直到满足终止条件。

4　仿真结果分析

电动机额定电压为270 V，控制信号电压范围为-10 V～10 V，选用的晶闸管开关频率为20 kHz，设定整流环节Ts=0.05×10-3s、Ks=27，系统其余仿真参数如表1所示。

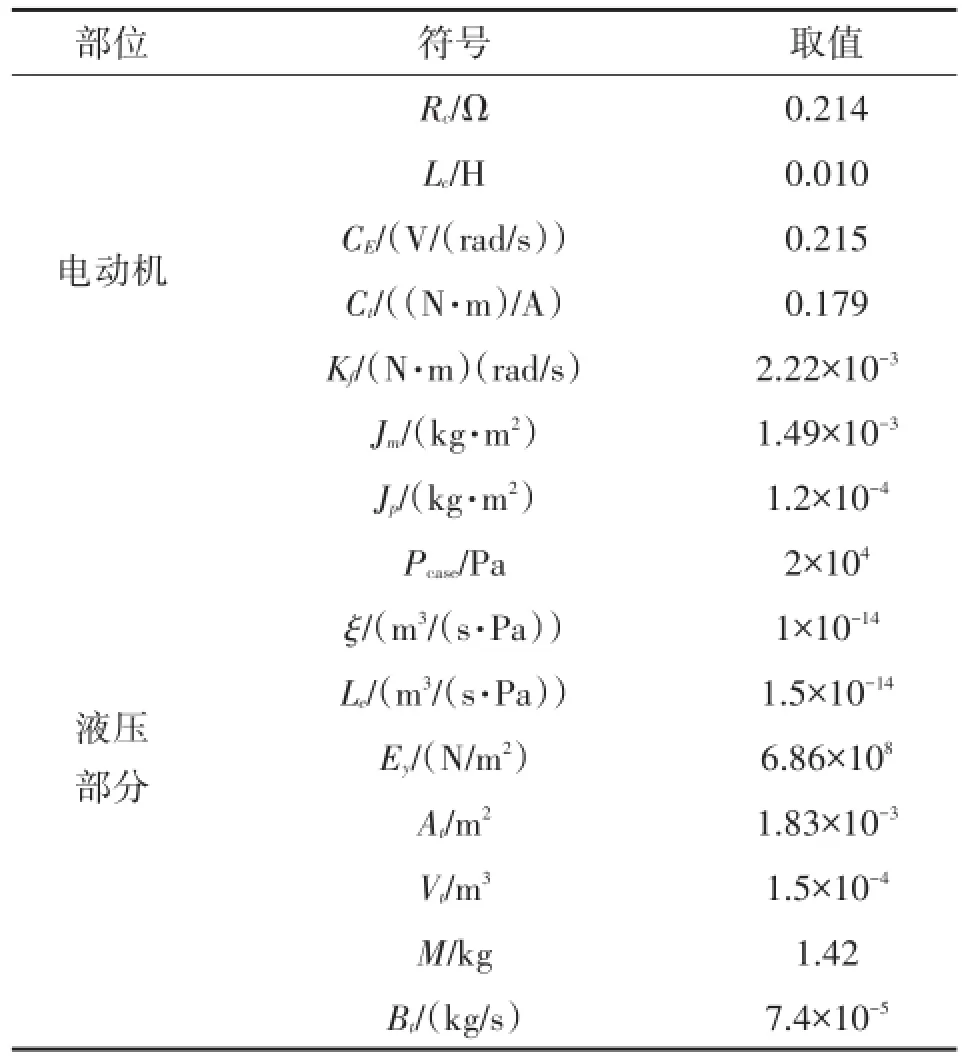
表1　系统仿真参数

为了验证经过AGA优化后控制参数对于EHA系统的有效性，采用Ziegler-Nichols阶跃响应法与SGA作为对照，在SGA中取Pc=0.6、Pm=0.01，表2列出了分别利用这3种方法得到的调节器参数。

表2　EHA控制器参数整定结果

将表中3组控制系统参数分别代入EHA仿真模型，当给定作动筒位置信号为0.01 m、舵面负载力为5 000 N时，系统的阶跃响应如图5所示。

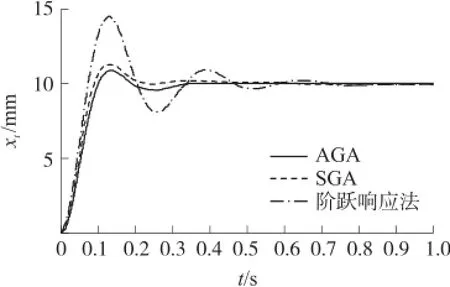
图5　EHA位置阶跃响应

经过对比分析不难得出，利用AGA优化后的控制器参数使EHA能够对信号作出快速响应并且受扰动影响小，同时具有更小的超调量、更高的精确度与稳定性，表3列出对应的系统输出结果。

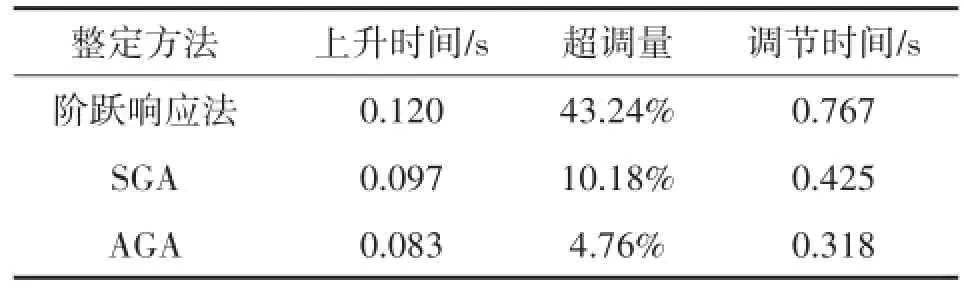
表3　系统输出结果

设计的EHA系统性能指标J是一个多峰值非线性函数，随着进化代数增加而逐渐减小直到收敛于一个常数，下面分别给出了SGA与AGA对控制参数优化过程中种群的最大适应度值变化曲线，以说明经过自适应处理后的GA优势。

从图6可以看出，通过引入自适应规则实时地改变交叉与变异概率，能有效地加快算法的收敛速度，随着劣质解逐渐被淘汰，种群的最大适应度值最终保持在55.47，在全局范围内搜索到的最优解对EHA具有更好的控制效果。

图6　优化过程中性能指标的变化

5　结论

一体化电静液作动器取消了传统的集中式液压系统，在未来航空航天领域将得到广泛地应用，具有重要的研究价值和现实意义。本文设计的位置、转速及电流三闭环负反馈串级连接的控制系统充分考虑了机载设备的性能指标要求，在利用遗传算法对控制器参数进行优化的过程中采取实数编码与自适应变化的交叉与变异概率，有效地防止了算法陷入局部最优解并保证了计算精度与搜索效率，经过选择算子、非均匀算术交叉算子及变异算子操作所得到的控制参数达到了EHA快速性、稳定性与精确度的设计目标，解决了常规PID整定方法难以实现复杂非线性系统理想控制效果问题。

［1］张晓娟.电动静液作动器的设计与研究［D］.西安：西北工业大学，2012.

［2］Zhang Y，Fu Y L，Zhou W X.Optimal Control for EHA-VPVM System Based on Feedback Linearization Theory［C］//ICCARV 2010：2010 International Conference on Control Automation Ro⁃botics and Vision.Singapore，2010：744-749.

［3］窦艳艳，钱蕾，冯金龙.基于MATLAB的模糊PID控制系统设计及仿真［J］.电子科技，2015，28（2）：119-122.

［4］曹玉丽，史仪凯，袁小庆，等.自平衡机器人变论域模糊PID控制研究［J］.计算机仿真，2013，30（2）：347-350.

［5］黄丽莲，周晓亮，项建弘.分数阶PID控制器参数的自适应设计［J］.系统工程与电子技术，2013，35（5）：1064-1069.

［6］葛继科，邱玉辉，吴春明，等.遗传算法研究综述［J］.计算机应用研究，2008，25（10）：2911-2916.

［7］赫英凤，段富海，金霞，等.电静液作动器不确定性建模分析与可靠度计算［J］.机械科学与技术，2014，33（12）：1937-1942.

［8］朱俊杰，粟梅，王湘中，等.无位置传感器无刷直流电机闭环三段式启动策略［J］.仪器仪表学报，2013，34（1）：173-179.

［9］Rojas I，Vinnett L，Yiannatos J，et al.The Optimization of Inter⁃face Interactivity Using Gesture Prediction Engine［J］.Technolo⁃gy Journal，2014，68（2）：558-565.

［10］蹇洁，王旭，葛显龙.云自适应遗传算法有能力约束的车辆调度优化［J］.重庆大学学报，2013，36（8）：40-46.

［11］Li S J，Shao L T，Wang J Z，et al.Inverse Procedure for Determin⁃ing Model Parameter of Soils Using Real-Coded Genetic Algo⁃rithm［J］.Journal of Central South University of Technology（Eng⁃lish Edition），2012，19（6）：1764-1770.

［12］朱宗斌，杜中军.基于改进GA的云计算任务调度算法［J］.计算机工程与应用，2013，49（5）：77-80.

谢鹏（1983-），男，河南驻马店人，空军工程大学理学院讲师，研究方向为网络与数据库集成，xpf68@163.com。

EEACC：723010.3969/j.issn.1004-1699.2016.06.020

基于自适应遗传算法的EHA控制器优化设计*

谢鹏*，张红梅
（空军工程大学理学院，西安710038）

为了解决电静液作动器（EHA）动态响应特性难以达到飞控系统要求的问题，设计了位置、转速及电流三闭环负反馈串级连接控制方案，提出了利用自适应遗传算法（AGA）对控制器参数优化方法。首先，建立了系统数学模型，在带限幅输出的转速与电流PI调节器中加入积分分离项以避免饱和；其次，考虑到标准遗传算法（SGA）早熟收敛与计算效率低，对交叉与变异概率采取随种群自适应变化策略，使用精度更高的实数编码，分析系统性能指标要求后在ITAE中引入适当加权的上升时间与调节器输出并采用惩罚功能以约束超调量；最后，通过MATLAB跨空间参数组的传递将算法与Simulink模型有机地结合起来完成了PID参数整定过程，使系统上升时间减少到0.083 s、超调量减小到4.76%、调节时间减少到0.318 s。实验结果表明，利用AGA优化后的控制器能有效地提高EHA系统的快速性、精确度与稳定性。

电静液作动器；自适应遗传算法；实数编码；参数传递；优化设计

TP273+.1；TP391.9

A

1004-1699（2016）06-0909-06

2016-02-26修改日期：2016-03-21

项目来源：军队级科研项目（KJ2013117）