Genetic Algorithms of Electromagnet in Longitudinal Wave Electromagnetic Utrasonic Dtection for Auminum Pate*

TAN Liangchen，WU Yunxin*，SHI Wenze，GONG Hai，FAN Jizhi（1.College of Mechanical and Electrical Engineering，Central South University，Changsha 410083，China；2.State Key Laboratory of High Performance Complex Manufacturing，Changsha 410083，China；3.Nonferrous Metal Oriented Advanced Structural Materials and Manufacturing Cooperative Innovation Center，Central South University，Changsha 410083，China）



Genetic Algorithms of Electromagnet in Longitudinal Wave Electromagnetic Utrasonic Dtection for Auminum Pate*

TAN Liangchen1，2，3，WU Yunxin1，2，3*，SHI Wenze1，2，GONG Hai1，2，FAN Jizhi1，2
（1.College of Mechanical and Electrical Engineering，Central South University，Changsha 410083，China；2.State Key Laboratory of High Performance Complex Manufacturing，Changsha 410083，China；3.Nonferrous Metal Oriented Advanced Structural Materials and Manufacturing Cooperative Innovation Center，Central South University，Changsha 410083，China）

An original electromagnet genetic algorithm method for improving the detectability of Electromagnetic Acoustic Transducer（EMAT）is introduced.Firstly，Magnetic induction and uniformity were the targets for the sin⁃gle-objective optimization respectively.The response surface methodology was employed to analysis the importance of magnetic core，coil on magnetic induction and uniformity，and on top of that，built a second-order response model to get optimum parameter groups.Secondly，Multi-objective optimization was adapted further considering the unifor⁃mity of magnetic field，it was optimized by co-simulation of Matlab and Comsol software using genetic algorithm，the consequence based on multi-objective optimization comparing with RSM was more accurate and it was significantly increased comparing with the initial value.At last，the effectiveness of the optimization method was proved by the experiments，and the experimental longitudinal wave signal rise by 60%，so the method can be applied to the other forms of electromagnet.

electromagnetic acoustic transducer（EMAT）；electromagnet；response surface methodology（RSM）；multi-objective optimization；genetic algorithm（GA）

电磁超声检测产生于20世纪60年代，相比于传统的压电超声检测技术，它具有无接触性、环保性、和较强环境适应性等突出特点，因而在近年得到了快速发展，已经广泛应用于金属板材、管材测厚，缺陷探伤，在线检测等多个领域［1-3］。国内外众多学者对电磁超声检测的核心电磁超声换能器（Electromagnetic Acoustic Transducers）进行了多方面的研究，Kawashima，Ludwig R等人重点研究了EMAT的换能原理，通过解析法或数值分析法建立EMAT模型，对EMAT在铝板中激发的声场进行分析［4］。王淑娟，翟国富研究团队对EMAT接收和激发过程进行三维建模，分析优化了EMAT结构，较大的提高了EMAT的换能效率［5-6］。江念等通过对EMAT的结构参数以及尺寸参数进行合理优化设计，提高其换能效率［7］。Steve Dixon团队侧重对激发线圈的高温性能拓展，通过陶瓷线圈实现EMAT在高温检测中的应用［8-10］。

目前针对EMAT的研究集中在激发、接收线圈部分，对于偏置磁场一般采用永磁铁处理，但是永磁铁的高温易失效且磁场时刻都存在，进行铁磁性材料检测时移动极为不便，Steve Dixon团队在进行高温检测时首先提出了利用电磁铁代替永磁铁的方案，利用电磁铁提供偏置磁场实现了高温检测，取得了较好的效果。王淑娟团队也在研究中使用电磁铁替代的方案，应用蝶形激发线圈进行电磁超声检测的研究［11］。电磁铁作为重要的产生磁场的结构形式，在电磁继电器，线性电磁开关，磁悬浮等领域有广泛的应用。Do-Kwan Hong利用有限元法计算磁悬浮设备中的电磁铁装置的磁力并进行优化，提出C型电磁铁的长度、高度、叠加厚度对磁力和动态性能有明显影响［12］。Hyun-Mo Ahn等研究磁力启动器中的电磁机构，提出磁芯的叠加厚度对电磁机构的动态性能影响最大［13］。翟国富等利用空间映射算法研究继电器，针对继电器的动态性能对电磁铁结构进行了优化设计［14］，竺冉等根据磁致伸缩导波的检测应用，对偏置磁场进行优化设计［15］。

电磁铁应用于电磁超声检测，其作用在于提供偏置磁场，偏置磁场方向与激发线圈中电流方向的差异可以产生超声纵波和超声横波，纵波相对于横波在同种材料中波长更长，衰减更小，有利于较厚的试样的测试且在传统压电超声中有更广泛的应用［16］。EMAT纵波检测能够更有效利用传统压电检测的经验，同时丰富EMAT的检测方式，因此EMAT纵波检测的研究有积极的意义。确定超声波检测形式决定了偏置磁场和激发线圈的位置关系，此时磁感应强度和磁场均匀度直接影响了EMAT检测的信号强度，因此本文重点研究了提高磁感应强度和均匀度的方法。

本文建立适用于EMAT纵波检测的二维电磁铁模型，通过有限元法计算目标区域的磁感应强度，然后分析电磁铁结构参数对磁感应强度和均匀度的影响，在此基础上进行单目标和多目标优化，将优化前后磁感应强度、均匀度进行对比，最后通过实验验证。

1　EMAT机理及控制方程

电磁超声检测的核心是EMAT，一般的换能器由接收与激发线圈、磁体、被测试样3部分组成。如图1所示，在非铁磁性材料中，电磁超声主要以洛伦兹力激励为主，EMAT线圈中通过高频、大功率的电流，其在被测试样内部产生与之流向相反的感生涡流JE，此时被测试样的集肤层内相当于有电流流过，永磁铁的静态磁场B与感生涡流相互作用产生洛伦兹力F，由于感生涡流为高频变化的，因此产生的洛伦兹力在试样的表面产生，试件内质点在力的作用下产生高频振动，这种振动以超声波形式产生并向内部传播。超声波产生过程表示为：

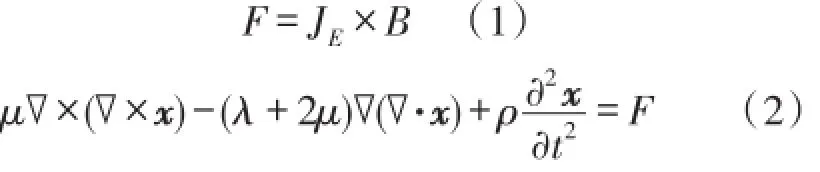
式中：λ和μ为拉梅常数；x为超声波位移矢量；ρ为材料密度。

接收过程中，根据法拉第电磁感应定律，存在偏置磁场B的情况下，由于超声振动接收线圈将感生交变电场Er， 计算方程如下：

根据超声波振动和传播方向的区别区分为横波和纵波。

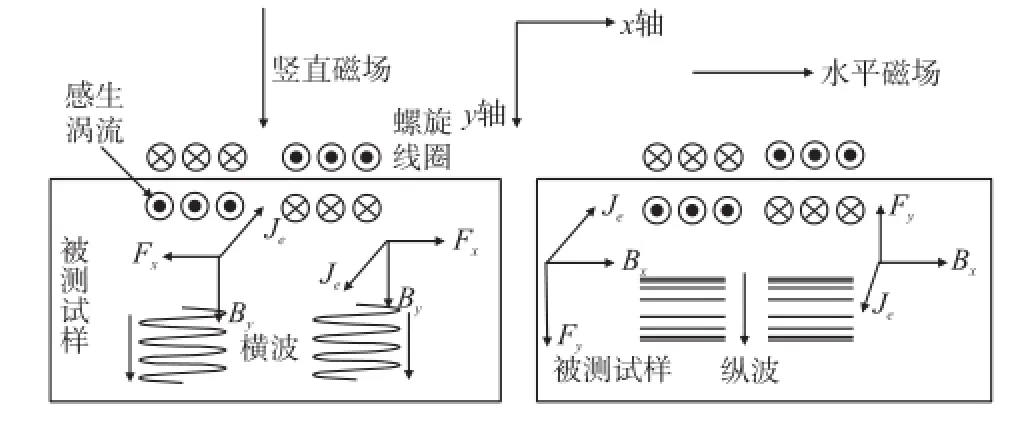
图1　EMAT体波结构示意图

2　电磁铁结构参数设计与分析

2.1电磁铁结构参数设计

目前在EMAT中应用最广的是永磁铁，但是由于永磁铁受温度影响大且移动不便，在高温或在线检测时存在局限，而采用电磁铁的形式则可有效解决这一问题。

电磁铁主要由骨架、磁芯和线圈组成。根据磁芯的结构可以将电磁铁分为E型，I型，C型等多种形式。其中E型，I型电磁铁主要产生竖直方向的磁场，通过高频线圈激发横波，C型电磁铁水平方向磁场占优，可以激发纵波。横波与纵波相比，同种材料中横波的波长更短，缺陷检测能力更强；纵波的波长长，衰减较小，在试件测厚中有更广泛的应用，且目前在无损检测应用较广的压电超声检测更多的使用纵波进行检测，研究EMAT激发纵波进行检测能更有效的利用传统压电超声经验，更有利于推广运用。因此采用C型电磁铁（如图2所示）激发纵波进行超声检测。

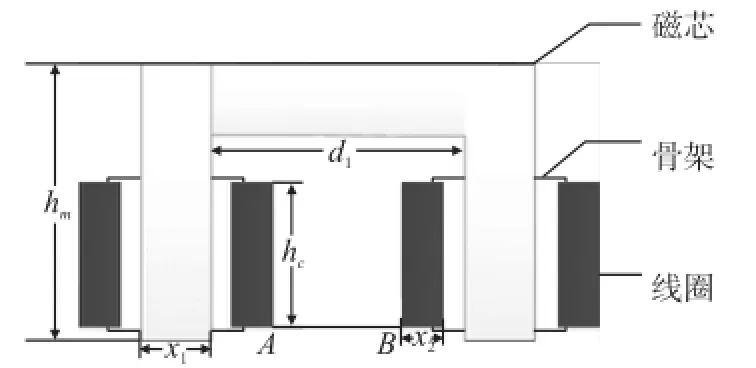
图2　C型电磁铁结构

C型电磁铁主要结构参数为磁芯的宽度x1，磁芯的高度hm，线圈绕制宽度x2，线圈绕制高度hc，磁轭长度d1。依照文献［17］的传统直流电磁铁计算方法，表示为：

式中，NI表示安匝数；Q表示线圈填充系数；JA表示电流密度；S表示导线的截面积；Deq表示线圈的平均等效直径，ρ为导线的电阻率，U为电源提供的电压。

2.2电磁铁磁场分析

实验采用Dell N305P-06台式机电源，功率305 W，为电磁铁供电，最大供电电压为24 V，根据结构形式选择电流密度JA为3 A/mm2，填充系数Q为0.35，综合考虑磁芯与线圈的相对关系及式（4）、式（5）得到C型电磁铁的电磁铁磁芯高50 mm，宽度17.5 mm，磁芯厚度为20 mm，线圈高度为35 mm，一般激发接收线圈大小为25 mm～30 mm，线圈放置于AB范围内，因此选择磁轭长度为65 mm。

电磁铁的磁场分析集中在激发、接收线圈与试样之间的区域。为简化计算，假设磁芯的磁导率由材料的磁化曲线决定，忽略磁芯的磁滞效应以及涡流效应；忽略由于电磁铁电感对磁场建立的影响，仅考虑稳定情况下磁场分布。

仿真参数设置励磁线圈匝数为170匝，通电电流为6 A，励磁线圈直径为0.38 mm，线圈等效电阻4.2Ω磁芯材料采用DW35型硅钢，建立二维模型进行磁感应强度仿真计算，同时采用lakeshore 460三通道高斯计测试在AB线范围内电磁铁产生的水平方向磁感应强度BX，将测试结果与仿真结果进行对比，建模计算结果和实验吻合良好，证明仿真计算的准确性。

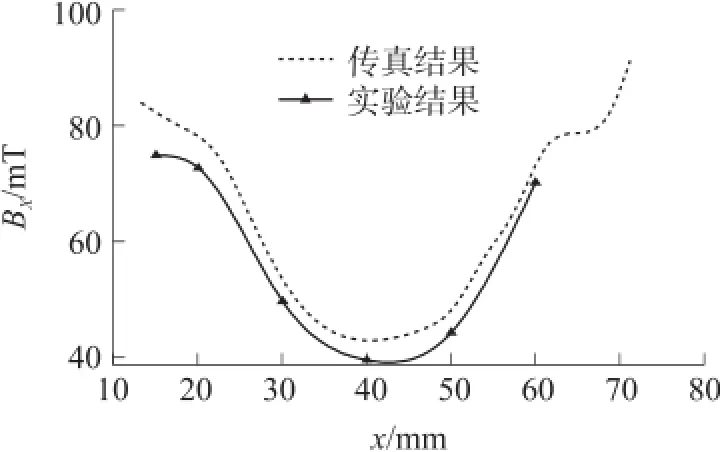
图3　仿真与实验结果对比

3　电磁铁磁场优化设计

电磁铁磁感应大小的决定性因素在于安匝数，安匝数越多对应的磁感应强度越大。但是安匝数越多会引起电磁铁体积增大，提高对供电电源的功率要求，这对于电磁超声的检测时不利的，因此本文的研究重点在于安匝数一定，由文献［17］计算确定电磁铁的基本体积，在建立的有限元模型基础上提取影响磁感应强度和均匀度的关键因素，分析各个因素的影响，通过几何结构参数的调整，最大限度的提高EMAT检测的信号强度，提升检测能力。

3.1响应曲面法优化设计

电磁铁的多个参数对磁感应强度和均匀度有影响且参数变化引起的有限元计算复杂，本文采用响应曲面的方法进行优化设计。响应曲面方法是现代质量工程中的一项重要的工具，它采用序贯的思想，先设计恰当的试验参数，然后根据试验结果数据进行回归拟合建立响应曲面模型，近似地反映目标变量与设计变量的函数关系，再对该模型进行分析，寻找最佳组合［18］。一般响应曲面法采用低阶多项式进行逼近拟合，

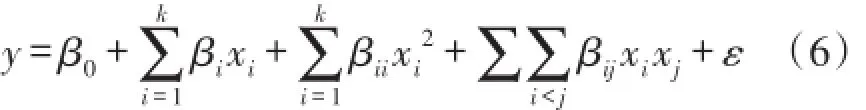
其中，β0表示xi的线性效应，βij表示xi与xj之间的线性交互作用，βii表示xi的二次效应，ε表示误差项，不能由y包含的变异部分，假定在不同的试验中是相互独立的，且服从均值为0方差为σ2正态分布。

3.1.1设计变量及范围

根据电磁铁的结构特性确定磁芯的宽度x1，取值范围为12 mm～24 mm；磁芯的高度hm，取值范围为48 mm～58 mm；线圈绕制宽度x2，取值范围为10 mm～14 mm；线圈绕制高度hc，取值范围为30 mm～46 mm；磁轭长度d1，取值范围为30 mm～70 mm。

3.1.2目标变量

偏置磁场的强度和均匀度均影响最后EMAT信号的优劣，理想优化算法对进行磁场均匀度和强度的多目标优化，但在响应曲面法中难以实现，综合考虑磁感应强度与均匀度对EMAT检测信号的影响，分别选择磁感应强度f1和磁场均匀度f2为作为优化目标，f1为图4所示EMAT激发、接收线圈的有效区域AB的平均磁感应强度。磁场均匀度f2，计算方式如下所示：

式中：Bmax，Bmin分别表示EMAT线圈区域的水平方向磁场最大值与最小值。

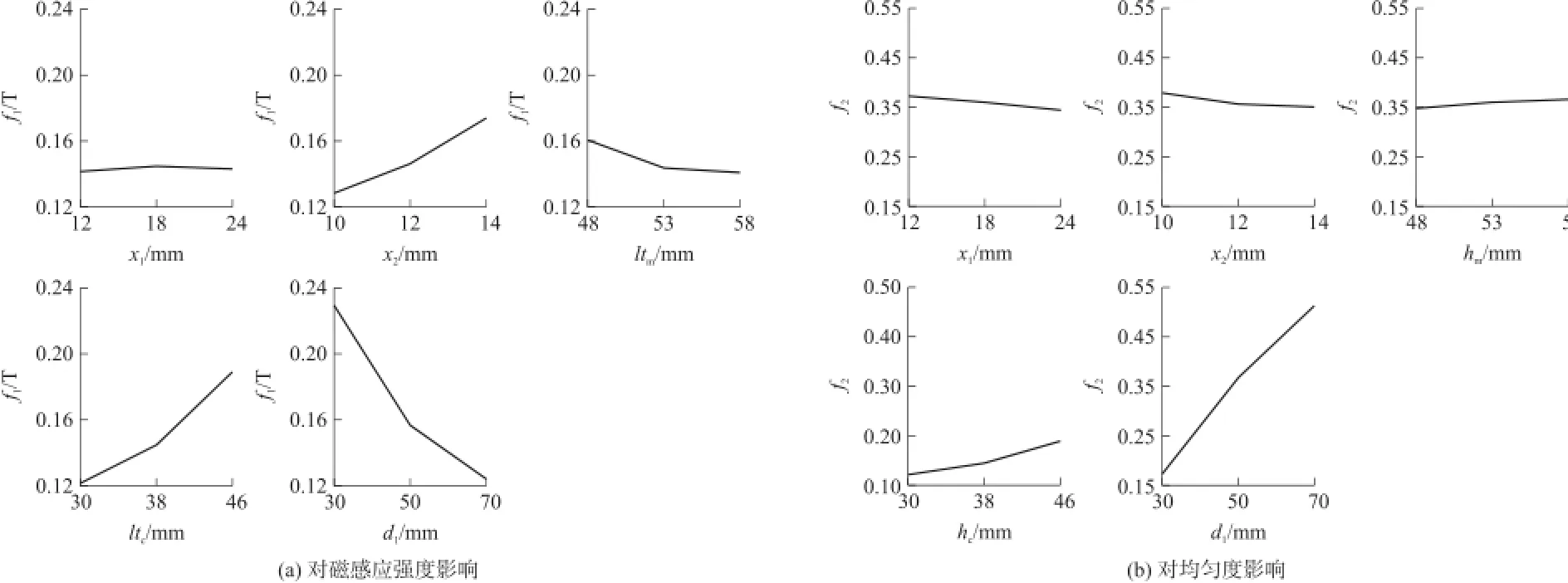
图4　设计参数对优化目标影响

3.1.3优化结果分析

利用Box-Behnken响应曲面法的设计原理，设计了五因素三水平的响应曲面分析试验，其正交表如表1所示，按照表1的参数修改有限元模型，分别计算各个参数组合下，磁感应强度大小及磁场均匀度。

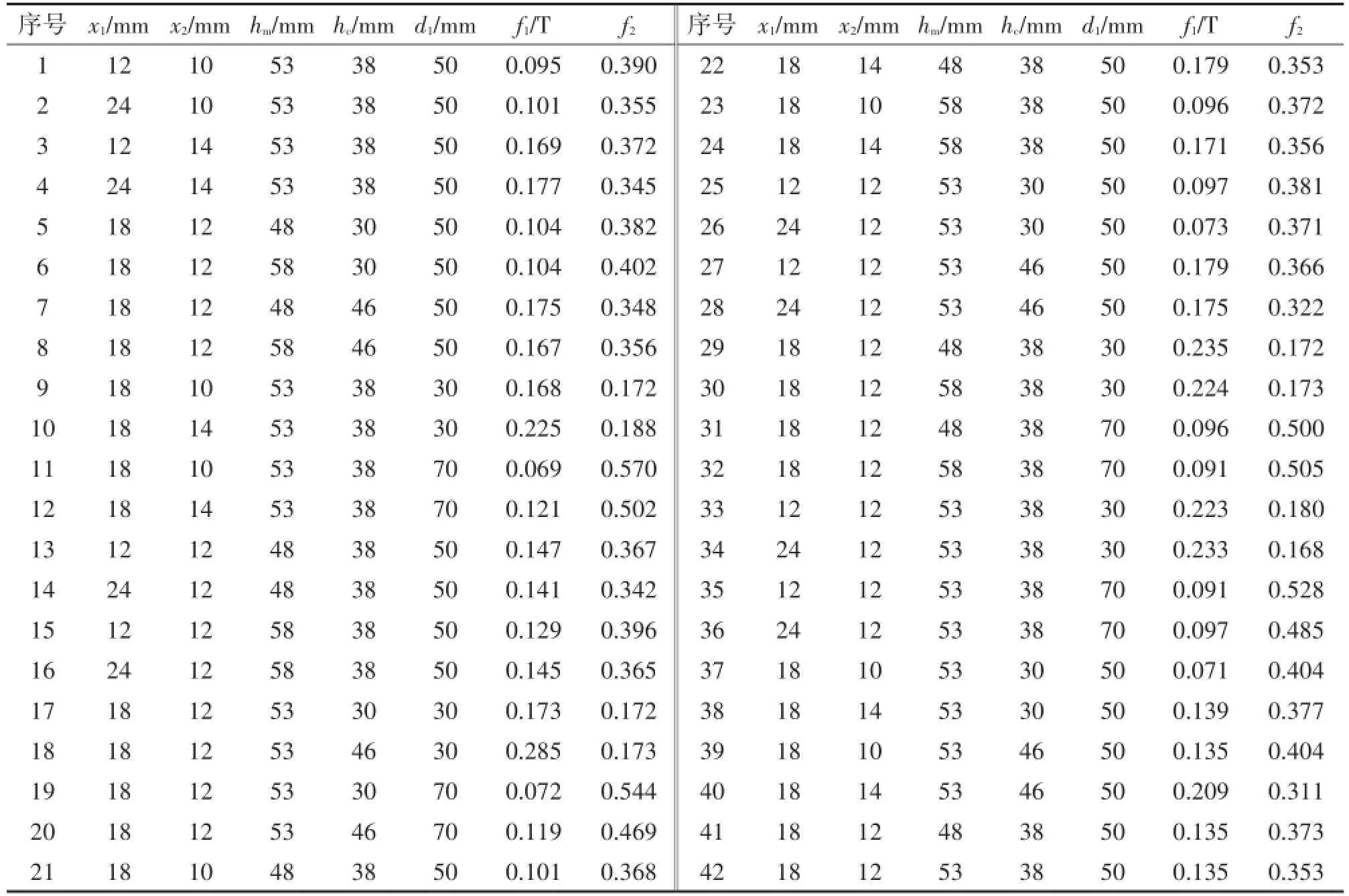
表1　电磁铁参数5因素3水平正交试验表

由正交实验表结果，计算各因素在相同水平下的算术平均值。例如分析磁芯的宽度x1对磁感应强度的影响，计算处于12 mm，18 mm，24 mm水平时磁感应强度的算术平均，分别为0.141 T，0.145 T，0.143 T。依次计算x2，hc，d1在3个水平下磁感应强度的变化，得到如图4的结果，曲线变化明显的因素对磁感应强度影响大，即x2，hc，d1三个因素对磁感应强度影响大；而磁轭距离d1对均匀度影响最明显，此时，利用响应曲面优化法，利用最小二乘法求得式（6）系数，分别建立平均磁感应强度和均匀度与设计变量的多元回归式（8）。

对式（8）建立的拟合模型进行适应性检验，选择R2检验作为适应度检验标准

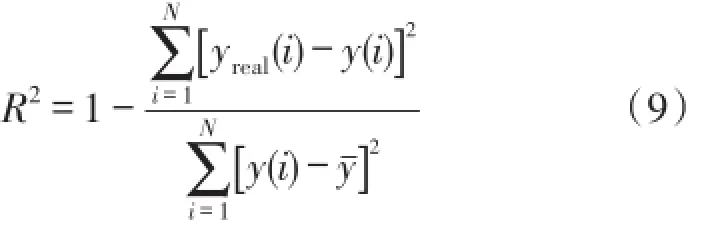
其中yreal（i）和y（i）分别是设计空间上各点的有限元计算值和响应面计算值，y¯是设计空间上各点真值的均值，此处为有限元计算的平均值，N是设计空间上检验点的数量，此处为42。计算式（9）得到适应度大小分别为96.01%，97.43%证明拟合模型是适合有效的。再利用式（8）建立的响应曲面，进行优化分析，得到优化参数如表2所示。

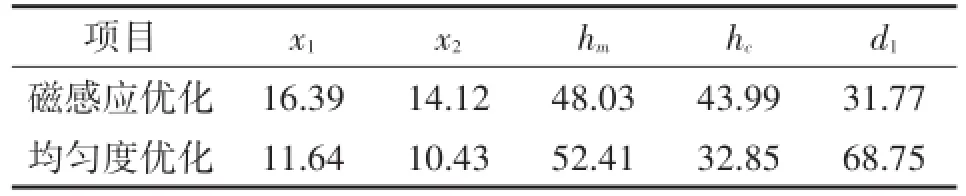
表2　响应曲面法参数优化结果

3.2多参数遗传算法优化设计

响应曲面法通过选取有限个试验点进行计算分析，采用统计学方法拟合出目标变量与设计变量的函数关系，然后进行优化。上节中考虑到响应曲面法对多目标优化的局限性，在进行响应曲面分析时进行简化只考虑了磁感应强度指标。

为更好的对电磁铁的结构参数优化，研究中采用Matlab与Comsol联合的方法，在设计变量不变的情况下，考虑磁感应强度和均匀度两个目标进行优化。

针对这一多目标优化问题，通过权重系数转化为单目标优化问题进行处理，以X方向磁感应强度f1和均匀度f2分别进行单目标优化，优化结果倒数作为权重系数的指标分量，

由于f1，f2数量级不统一且不满足权重系数为1的条件，因此进行归一化处理。

将m1，m2数量级统一，则有

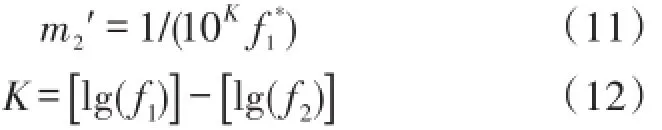
其中K表示调整系数，［*］为高斯取整函数。

此时归一化权重系数ωi（i=1，2）为：

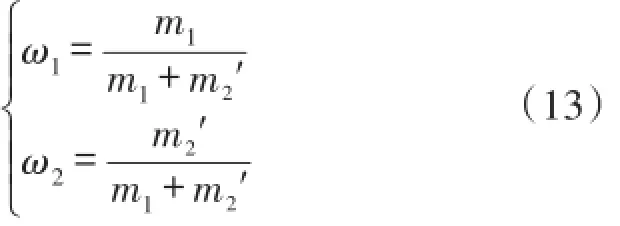
最终的单一优化目标feq。

将多目标转化为单目标后，先在Comsol中根据图2所示的几何结构建立二维有限元模型，其中设置磁芯为硅钢，磁化B-H曲线如图5所示，电磁铁绕制铜导线电导率2.667×10-7S/m，空气相对磁导率1，空气域的面积为几何模型面积的8倍，采用自适应网格划分，空气域网格尺寸采用预设的正常尺寸，在磁芯和线圈区域进行网格细化，控制网格最大尺寸为0.01 mm，最小尺寸为0.036 mm，生长率为1.5；选择电磁场模块并用稳态求解器求解，求解器的相对容差设置为0.01。

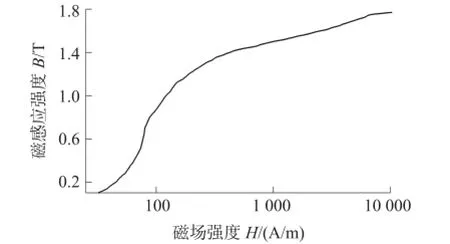
图5　硅钢片磁化B-H曲线

再采用图7所示的优化过程进行计算。经过多次试验，确定遗传算法的参数如表3所示，优化结果如表4所示。

表3　遗传算法工具箱参数设置

表4　遗传算法参数优化结果

分别根据响应曲面优化设计法和遗传算法的参数优化结果结合有限元模型计算目标区域的x方向磁感应强度如图6所示，采用响应曲面法设计结果与遗传算法比较，多目标优化相比单一的磁感应强度优化，在有效区域内的磁感应强度更大，均匀度更好，相比单一均匀度优化，虽然均匀度稍差，但是磁感应强度大小为其2.0倍～2.4倍，综合比较采用遗传算法进行多参数优化效果最好。

图6　优化结果对比

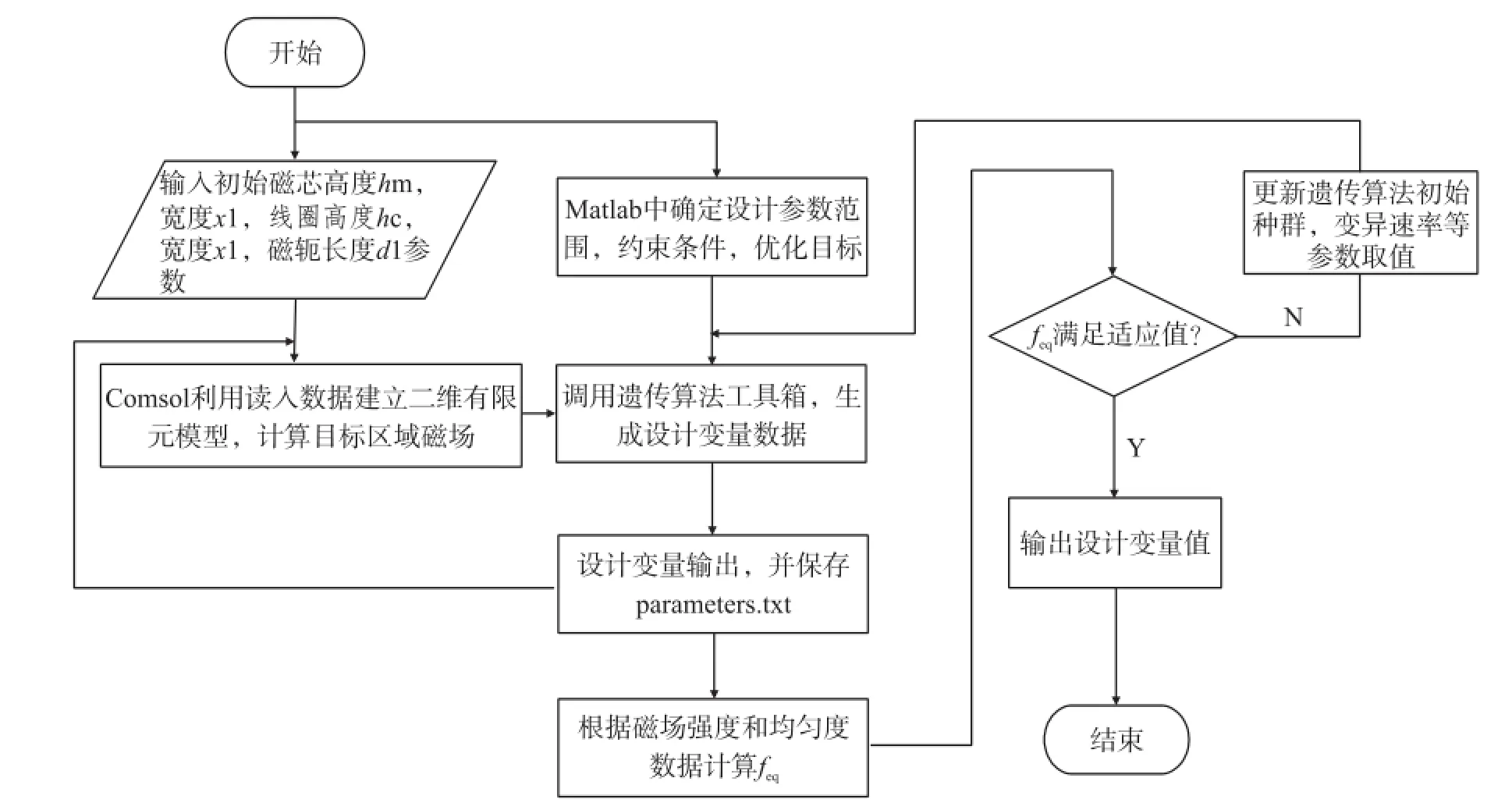
图7　Matlab与Comsol联合优化流程图

比较优化算法的设计参数，在EMAT纵波检测中，电磁铁有效磁场为水平方向分量，在设计中应在允许的情况下减小磁轭距离，磁轭越小，有效区域磁感应强度越大，线圈的绕制高度和绕制厚度对磁感应强度的影响巨大，需要合理设计，同时磁芯的高度和厚度也应与线圈匹配，磁芯设计太高或太厚，会使磁化难度增加，削弱磁感应强度；磁芯设计过矮或厚度不够则造成磁芯达到饱和时，磁感应强度仍然较小；磁轭是影响均匀度的重要因素，但是仅优化均匀度会严重削弱磁感应强度，影响EMAT信号强度。

4　实验验证

采用自主搭建的检测平台验证优化方案的有效性，实验平台主要包括发射模块，接收模块，EMAT探头等部分。发射模块用于向EMAT探头的激发线圈输送高频大功率发射电流；接收模块用于接收EMAT探头的接收线圈的超声信号，并将信号进行放大，滤波和模数转换；EMAT探头作为传感器，是电磁超声检测的核心，包括接收线圈、激发线圈，电磁铁部分，接收和激发线圈均采用跑道型线圈，结构如图9所示，线圈导体直径0.35 mm，面积为60 mm×40 mm，匝数为30，，采用优化前后两种不同尺寸的电磁铁在200 mm×100 mm×70 mm的7050铝板上进行实验。

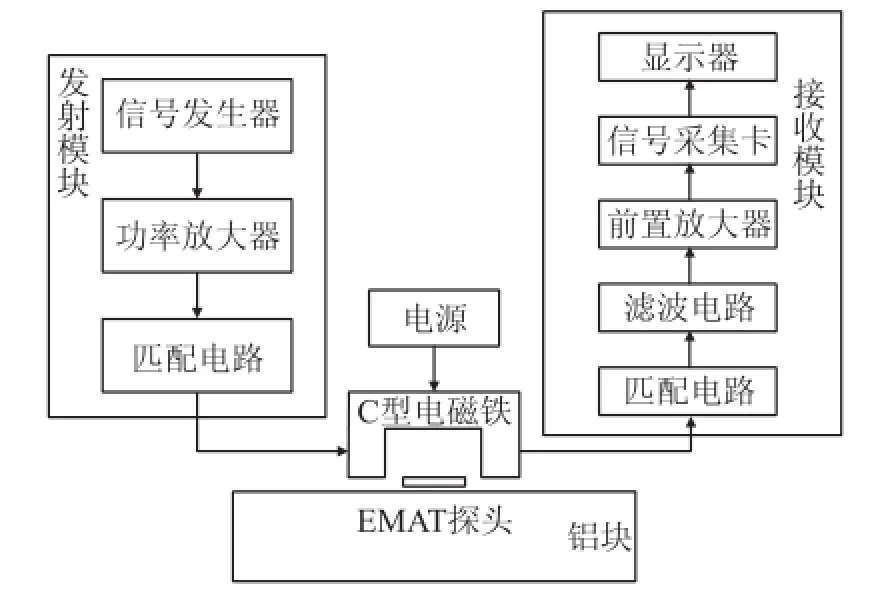
图8　试验系统结构框图

图9　跑道线圈示意图

实验结果如图10所示，信号幅值如表5所示，采用磁感应强度和均匀度多目标优化后纵波一次回波幅值AL提升至优化前的1.6倍，优化后横波一次回波幅值AS增加20%，有效的提高了检测信号的幅值，达到了优化目的。

图10　优化前后超声信号对比

表5　多目标优化前后信号强度对比

5　结语

本文提出在铝板纵波超声检测中的电磁铁优化方案，分别采用响应曲面法单目标优化和综合运用Comsol有限元软件与Matlab联合的多目标优化方案，并通过实验验证，分析结果表明：①通过响应曲面法结合有限元模型计算，在安匝数确定的情况下，电磁铁的磁轭长度，线圈的绕制宽度和高度为影响磁感应强度大小的主要因素，在电磁铁结构设计中需要重点考虑。②以有效区域的磁感应强度和均匀度为目标进行多目标优化，综合运用Comsol有限元软件与Matlab联合，采用遗传算法，得到优化参数。两种优化方式相比响应曲面优化时间短精度低，但是遗传算法优化可实现多目标优化，优化精度高，多目标优化目标区域磁感应强度提高1倍，实验验证优化后纵波信号幅值提高60%，优化更有效。③在电磁铁提供偏置磁场的EMAT检测中，受电源功率限制不能无限增加安匝数的情况下，通过优化电磁铁的结构参数，在体积基本不变的情况下有效提升EMAT信号的强度；本文以C型直流电磁铁为例进行了分析，在E型，I型电磁铁以及脉冲电磁铁设计中，可采取同样的思路方法进行优化。

［1］王淑娟，康磊，赵再新，等.电磁超声换能器的研究进展综述［J］.仪表技术与传感器，2006（5）：47-50.

［2］汪开灿，许霁，翟国富.基于电磁超声的铝板缺陷识方法［J］.浙江大学学报（工学版），2014，48（11）：2031-2038.

［3］Dixon S，Edwards C，Palmer S B.A Laser-EMAT System for Ultra⁃sonic Weld Inspection［J］.Ultrasonics，1999，37（4）：273-281.

［4］Kaltenbacher M，Ettinger K，Lerch R.Finite Element Analysis of Coupled Electromagnetic Acoustic Systems［J］.IEEE Transac⁃tions on Magnetics，1999，35（3）：1610-1613.

［5］王淑娟，康磊，李智超，等.电磁超声换能器三维有限元分析及优化设计［J］.中国电机工程学报，2009，29（30）：123-128.

［6］王淑娟，李智超，李鹏展，等.非铁磁材料表面波电磁超声换能器接收性能分析与优化设计［J］.中国电机工程学报，2015（9）：2360-2365.

［7］江念，王召巴，陈友兴，等.电磁超声检测钢板厚度实验的参数优化［J］.传感技术学报，2015，28（4）：498-502.

［8］Hernandez Valle F，Dixon S.Initial Tests for Designing a High Temperature EMAT with Pulsed Electromagnet［J］.NDT&E In⁃ternational，2010，43（2）：171-175.

［9］Hernandez-Valle F，Dixon S.Pulsed Electromagnet EMAT for Ul⁃trasonic Measurements at Elevated Temperatures［J］.Insight-Non-Destructive Testing and Condition Monitoring，2011，53（2）：96-99.

［10］Burrows S E，Fan Y，Dixon S.High Temperature Thickness Mea⁃surements of Stainless Steel and low Carbon steel Using Electro⁃magnetic Acoustic Transducers［J］.NDT&E International，2014，68（1）：73-77.

［11］ZHANG Heng，SU Riliang，WANG ShuJuan，et al.Design of Bulk Wave EMAT Using a Pulsed Electromagnet［C］//FENDT 2014—Proceedings.New York：IEEE，2014：242-246.

［12］Hong D，Woo B，Koo D，et al.Electromagnet Weight Reduction in a Magnetic Levitation System for Contactless Delivery Applica⁃tions［J］.Sensors，2010，10（7）：6718-6729.

［13］Hyun-Mo Ah，Yeon-Ho Oh，Ki-Dong Song，et al.Optimal Design of Permanent Magnetic Actuator for Permanent Magnet Reduction and Dynamic Characteristic Improvement Using Response Sur⁃face Methodology［J］.Journal of Electrical Engineering and Tech⁃nology，2015，10（3）：935-943.

［14］Zhai Guofu，Wang Qiya，Ren Wanbin An.Output Space-Mapping Algorithm to Optimize the Dimensional Parameter of Electromag⁃netic Relay［J］.IEEE Transactions on Magnetics，2011，47（9）：2194-2199.

［15］史亦伟.超声检测［M］.北京：机械工业出版社，2005.

［16］竺冉，吕福在，唐志峰，等.磁致伸缩纵向导波传感器中偏置磁场的优化设计［J］.传感技术学报，2011，24（3）：371-375.

［17］李泉凤.电磁场数值计算与电磁铁设计［M］.北京：清华大学出版社，2002.

［18］Montgomery D C.Design and Analysis of Experiments［M］.北京：人民邮电出版社，2009.

谭良辰（1992-），男，湖南常德人，硕士研究生，主要从事电磁超声无损检测技术的研究，tlc092@csu.edu.cn；

吴运新（1963-），男，博士，博士生导师、教授，主要从事机械结构动力学、无损检测、冶金机械研究，fjzcsu@csu.edu.cn。

EEACC：723010.3969/j.issn.1004-1699.2016.06.005

铝板纵波电磁超声检测中电磁铁的遗传算法优化设计*

谭良辰1，2，3，吴运新1，2，3*，石文泽1，2，龚海1，2，范吉志1，2
（1.中南大学高性能复杂制造国家重点实验室，长沙410083；2.中南大学机电工程学院，长沙410083；3.中南大学有色金属先进结构材料与制造协同创新中心，长沙410083）

提出一种提升电磁超声检测能力的电磁铁的遗传算法优化方法，首先采用单目标优化方法，分别以磁感应强度和均匀度为目标，利用响应曲面法（RSM），确定磁感应强度与磁芯，线圈等因素的二阶响应模型，根据响应模型得到优化参数。然后采用多目标优化方法，以磁感应强度和均匀度为目标，采用Matlab与Comsol联合仿真，并结合遗传算法进行优化。两组优化结果表明：多目标优化方法得到的有效区域磁感应强度更高，均匀度更好，通过实验证明优化后纵波信号提升60%，证明优化方法有效，可以将该方法运用到其他形式的电磁铁设计。

电磁超声换能器；电磁铁；响应曲面法；多目标优化；遗传算法

TB552

A

1004-1699（2016）06-0813-08

2015-12-29修改日期：2016-03-01

项目来源：国家科技支撑计划基金项目（2014BAF12B01）；高性能复杂制造国家重点实验室自主研究课题基金项目（zzyjkt2013-06B）