Gas Concentration Dynamic Prediction Method of Mixtures Kernels LSSVM Based on ACPSO and PSR*

FU Hua，DAI Wei（1.Faculty of Electrical and Control Engineering，Liaoning Technical University，Huludao Liaoning 15105，China；.College of Safety Science and Engineering，Liaoning Technical University，Fuxin Liaoning 13000，China）



Gas Concentration Dynamic Prediction Method of Mixtures Kernels LSSVM Based on ACPSO and PSR*

FU Hua1*，DAI Wei2
（1.Faculty of Electrical and Control Engineering，Liaoning Technical University，Huludao Liaoning 125105，China；2.College of Safety Science and Engineering，Liaoning Technical University，Fuxin Liaoning 123000，China）

In order to predict the gas concentration of coalface accurately，the gas concentration dynamic prediction method of mixtures of kernels least squares support vector Machine theory based on phase space reconstructiontheo⁃ry and adaptive chaos particle swarm optimization was proposed.This paper has the coalface gas concentration ob⁃tained by wireless sensor network monitoring system in underground to be the target，the noise of the gas concentra⁃tion was filtered by translation invariant de-noising method，the MK-LSSVM model was trained with gas concentra⁃tion time series data based on phase space reconstruction，and ACPSO algorithm was used to optimize the parame⁃ters of MK-LSSVM model，the prediction accuracy of the whole system was improvement by error correction method. The simulation result shows that，the dynamic prediction method we proposed was able to make prediction result fit the monitoring data well.And the mean absolute percent error was 0.024 1，the relative root mean square error was 0.209 7，the average relative variance was 0.003 11，the results were reasonable and meet the actual needs of the project，which can provide an effective theoretical basis forprediction and prevention work of mine gas.

gas concentration；dynamic prevention；phase space reconstruction；adaptive chaos particle swarm algo⁃rithm；measures-kernel LSSVM

预测工作面瓦斯浓度是防治瓦斯突出灾害的重要措施。受地质构造、煤层厚度等自然因素和开采技术的影响，采煤工作面瓦斯浓度呈现出显著的不均衡性和复杂性，目前，以瓦斯浓度作为研究对象进行预测、预警的方法较多，譬如灰色系统［3］、分形理论［2］、D-S理论［3］、支持向量机［4］、神经网络［5］等，这些方法都是对瓦斯浓度预测的有益探索。然而，在有限的瓦斯浓度观测数据中，瓦斯浓度的非平稳性和随机性对预测结果存在较大影响［6］，需要提高预测模型的精度和泛化能力。因此，提出用混合核最小二乘支持向量机MK-LSSVM（Mixtures Kernel Least Squares Support Vector Machine）网络拟合工作面瓦斯浓度与其历史瓦斯浓度数据之间的非线性函数关系，弥补单一核函数的不足；提出用自适应混沌粒子群优化算法ACPSO（Adaptive Chaos Particle Swarm Optimi⁃zation）所具有的全局搜索能力去获取MK-LSSVM模型的最优参数，同时构建误差校正模型，以提高预测模型的性能。建立相空间重构PSR（Phase Space Reconstruction）MK-LSSVM瓦斯浓度预测模型，实现工作面瓦斯浓度的快速、有效预测，为煤矿的安全监测监控提供良好的理论支持及技术指导。

1　瓦斯浓度时间序列相空间重构

瓦斯浓度序列可以描述为具有混沌非线性特征的时间序列，根据Takens定理，获取瓦斯序列中所蕴含的可以表征动力系统的初始特征信息，则需要创建多维状态空间，使之成为MK-LSSVM模型可用的输入矢量，即对瓦斯浓度时间序列进行相空间重构［7-8］。

对于瓦斯浓度时间序列｛x（t）｝（t=1，…N），根据相空间微熵率重构参数法［9］，以微熵率最小的方法选取合适的延迟时间τ与嵌入维数m进行相空间重构。重构后得到t时刻系统的动力学状态X（t）：

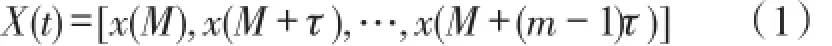
式中，M表示m维相空间中的点数且M=1，2，…，N-（m-1）τ。

在相空间中，延迟时间τ后的状态X′（t+τ）与当前的状态X（t）之间存在一个光滑映射F：Rm→Rm，则二者之间的关系满足式（2），则F（·）是系统的预测函数。

2　混合核函数最小二乘支持向量机

LSSVM在结构风险最小化原理基础上，弥补了神经网络泛化性能不高，小样本时精度低，大数据时“维数灾难”的缺陷；并且，其对高维数、非线性、小样本数据的处理能力会使煤矿瓦斯浓度动力系统实现更加准确的辨识与预测。由于受单一核函数的局限，LSSVM的预测精度过于依赖对核函数及其参数的选择的问题。为此提出MK-LSSVM模型，并将ACPSO算法与MK-LSSVM有机结合起来，进而改善其收敛速度与学习效率。从本质上提高MK-LSSVM的辨识性能和预测精度。

2.1LSSVM原理

定义样本LSSVM将逼近误差ξ的二次范数作为损失函数，优化问题可描述为

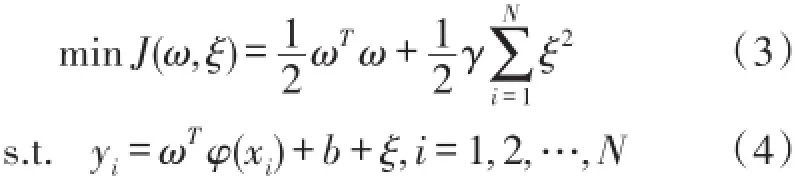
式中，J为损失函数，ω∈Rnh为权向量；ξ为经验误差，b为偏置量，γ是正则化参数，它是调节作用能够使所求得的逼近函数在具有良好泛化能力的前提下兼顾模型复杂度与训练误差，φ（·）：Rn→Rnh表示样本到高维空间的非线性映射。对偶问题Lagrange多项式为：

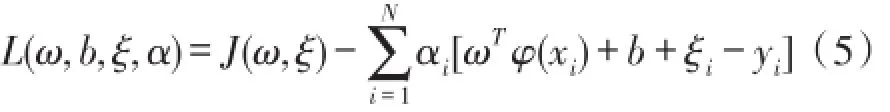
式中，αi为Lagrange乘子。对ω，ξi，b，αi分别求偏导数，得到最优解条件为

根据KKT条件，消去ω，ξi的方程组为：

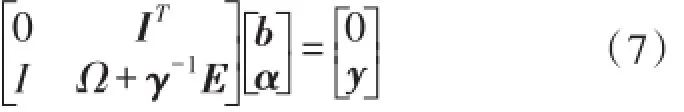
式中，I=［1，1，…，1］T；α=［α1，α2，…，αN］T；y=［y1，y2，…，yN］T；E是N×N维单位矩阵；Ω=K（xi，xj）是满足Mercer条件的核函数，Ω+γ-1E是核相关矩阵。

通过KKT条件求取参数α*、b*，LSSVM回归模型为：

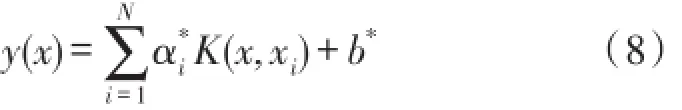
式中，K（x，xi）是LSSVM的核函数。

2.2MK-LSSVM模型

LSSVM中核函数的选择决定了模型的特性，局部核函数学习能力强、泛化性能弱，而全局核函数泛化性能强、学习能力弱［10-11］。为了使结构风险最小化，使真实风险达到最优，本文将综合局部核函数和全局核函数的优点，构造混合核函数以提高LSSVM模型的辨识和预测的精度。重新构造的混合核函数：

其中，λ∈［0，1］是混合权重系数，用来权衡不同核函数在混合核中的比重，即选择拟合精度和泛化能力间的折中。q是多项式核阶数，若q过大则会使模型维数增大，并降低泛化能力，所以文中采用二次多项式核。

因此，需要优化的混合核LSSVM参数分别是正则化参数γ、核参数σ和权重系数λ。

3　ACPSO优化混合核LSSVM模型

3.1基本粒子群优化算法

粒子群优化（PSO）算法是一种基于群体智能的全局优化进化算法。其规则简单，收敛的速度快，粒子更新自身的速度和位置：

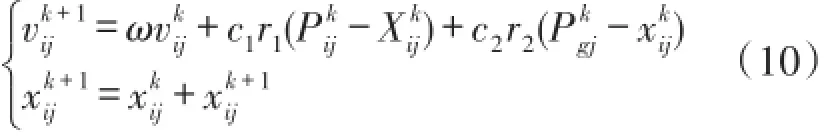
其中，i=1，2，…，m；j=1，2，…，d；k为当前迭代次数；ω为惯性权重；c1和c2是加速度因子，均为非负常数；r1和r2是分布于［0，1］区间式的随机数。Xi=（xi1，xi2，…，xid）T是第i个粒子的位置；Vi=（vi1，vi2，…，vid）T是第i个粒子的速度；Pi=（Pi1，Pi2，…，Pid）T是个体最优解，Pg=（Pg1，Pg2，…，Pgd）T是种群的群最优解［11］。

3.2惯性权重自适应调整

惯性权重体现了粒子继承先前的速度的能力，若惯性权重较大则有利于全局搜索，若惯性权重较小则有利于局部搜索。为了增强算法在全局和局部搜索之间的平衡，本文采用非线性递减策略的自适应调整惯性权重

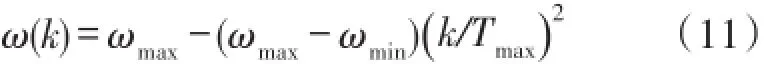
式中，ωmax、ωmin分别表示惯性权重的最大值和最小值，ki表示当前迭代次数，Tmax表示最大迭代次数。在初期，ω变化较慢，取值较大，维持了算法的全局搜索能力，而后期ω变化较快，极大地提高了算法的局部寻优能力，因此可以获得较好的收敛速度和精度。

3.3混沌扰动以及早熟判断机制

混沌优化算法具有较好的随机性和遍历性，因此在初始和进化过程中具有随机性特点的PSO算法中，引入混沌搜索思想，改善PSO算法摆脱局部极值点的能力，提高收敛速度和精度。本文采用典型的混沌系统Logistic映射，其方程是：

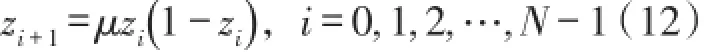
式中，μ为控制参量，设0≤z0≤1，取μ=4时，系统完全处于混沌状态。

当PSO算法收敛但又未获得理论最优解时，进化过程将处于停滞状态，算法陷入局部最优，此时，群体适应度方差应等于零或者接近于零。因此，以群体适应度方差作为判断粒子群早熟的依据，定义群体适应度方差δ2：

其中，fi是粒子i的当前适应度值，favg是当前种群的平均适应度值；f=max［1，max|fi-favg|］为归一化定标因子。δ2的值越小，表示群体的收敛性越好。

3.4ACPSO算法优化模型参数

瓦斯信号的非线性、复杂性、时变性等特征，使安全监测系统对瓦斯浓度预测模型的泛化能力和预测精度要求能够达到良好的预期效果。提出在PSO算法中引入混沌思想，结合定义的自适应惯性权重和群体适应度方差来平衡PSO算法的全局和局部搜索能力，得到一种自适应混沌粒子群优化算法，并用其优化混合核LSSVM模型参数，以提高模型的预测性能，具体优化步骤如下：

Step 1参数初始化：以混合核LSSVM模型的参数（γ，σ，λ）作为优化目标，设置粒子群的种群数num、学习因子与惯性权重ω范围、最大迭代次数Tmax等。

Step 2混沌初始化：随机产生一个d维向量zi=（zi1，zi2，…，zid），zi各分量在（0，1）之间，根据Logistic映射式（15）产生N个具有混沌特性的向量（z1，z2，…，zN），并将混沌特征向量按式（17）映射到优化变量的搜索区域。

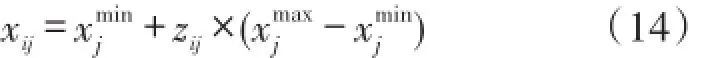
计算粒子的适应度值，选出其中m个适应度较好的作为初始粒子，再随机产生m个初始速度。

Step 3按式（11）自适应调整惯性权重，并按式（10）对粒子的位置和速度更新。计算各粒子的适应度值，更新个体粒子的最优值Pi和全局最优值Pg。

Step 4根据当前种群的适应度方差δ2，判断是否陷入早熟状态，若种群适应度方差δ2小于阈值，则转入Step 5，否则转入Step 3。

Step 5如果判断出粒子陷入早熟，则进行混沌扰动。对最优位置Pg=（Pg1，Pg2，…，Pgd）进行混沌优化。将Pgj（j=1，2，…，d）映射到Logistic方程的定义域［0，1］，再用式（12）进行迭代产生混沌变量序列，并将序列通过

Step 6判断是否满足终止条件，若不满足条件则返回Step 3，若满足终止条件，则输出全局最优解。

4　建立瓦斯浓度动态预测模型

瓦斯浓度动态预测系统结构如图1所示。

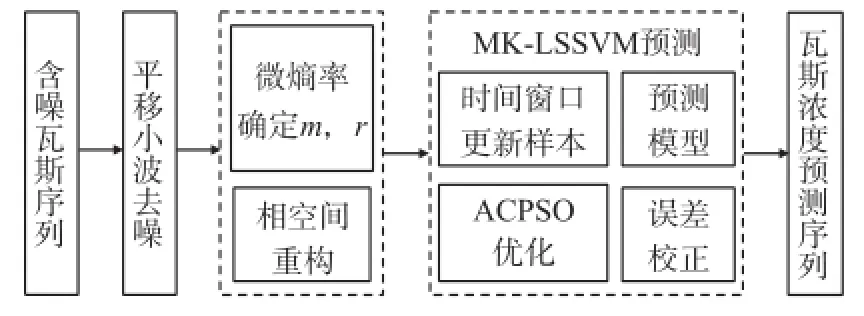
图1　瓦斯浓度动态预测系统结构示意图

建立瓦斯浓度动态预测模型的步骤如下：

①对传感器监测到的瓦斯浓度信号预处理，滤除噪声，再用Lyapunov指数对滤除噪声后的瓦斯浓度时间序列x（t）进行分析，用最小微熵率法选择合适的最佳嵌入维数和时延时间，对x（t）进行相空间重构。

②在重构的相空间中，以重构的数据样本作为MK-LSSVM的矢量输入，采用数据时间窗口滑动更新策略，以固定窗口为单位滚动更新样本，对模型进行学习训练，使模型中的核矩阵随样本的更新而相应的变化，保证预测系统能够反映瓦斯浓度的最新变化规律，以减小因随时间迁移引起的累积误差，提高模型的拟合精度。

③用ACPSO算法优化MK-LSSVM的模型参数（γ，σ，λ），使适应度值达到最小，将获得的最优参数反馈给MK-LSSVM模型。

本文定义MK-LSSVM模型的实际输出结果ŷi（x）与目标期望结果yi（x）的均方差作为适应度函数J（x）

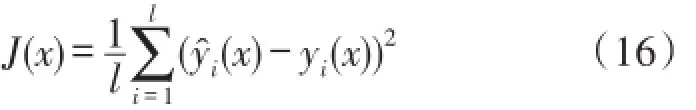
④通过误差校正方法提高MK-LSSVM模型的预测精度。定义训练误差集｛ek｝lk=1是训练样本在优化MK-LSSVM模型时所产生的训练误差，用｛ek｝lk=1建立MK-LSSVM误差预测模型，通过该模型对预测样本的误差进行预测，进而校正预测模型对瓦斯浓度的预测值，得到最终的瓦斯浓度预测序列。

5　瓦斯浓度预测实验及分析

5.1数据预处理

文中以来自开滦矿业集团钱营矿的瓦斯浓度监测数据为例，采集到的2015年5月某时段的500个瓦斯浓度数据样本，其曲线图如图2（a）所示。

图2　瓦斯浓度降噪处理

由于煤矿井下开采环境复杂，瓦斯浓度信号会受到各种干扰噪声的影响，因此，先用平移小波变换法对监测到的瓦斯浓度时间序列进行降噪处理，去噪后的瓦斯浓度时间序列如图2（b）所示，已经将原始监测瓦斯浓度序列中携带的干扰和毛刺剔除。用最大Lyapunov指数判断识别瓦斯浓度时间序列是否具有混沌特性［12］，本文根据文献［13］计算得到该时间序列的Lyapunov是0.036 728＞0，因此可以判断出瓦斯浓度时间序列具有混沌特性。

5.2预测过程

对去噪后的瓦斯浓度时间序列，用其中的样本1～470对模型作学习训练，用样本471～500做预测。根据微熵率法求取其嵌入维数m=6，时间延迟τ=3，相空间重构后得到455组样本，将重构的样本作为MK-LSSVM的输入矢量，采用滑动窗口更新训练样本，训练MK-LSSVM预测模型，同时ACPSO算法优化模型的参数，并通过误差校正提高模型的预测精度。其中，粒子群种群数为50，最大迭代次数为500，加速度因子c1=c2=2，ωmax=0.9，ωmin=0.4；模型训练的允许误差范围为10-4。

经ACPSO优化得到MK-LSSVM预测模型的最优参数为正则化参数γ=16.4325、核参数σ=200、权重系数λ=0.605。图3是用PSO和ACPSO优化MK-LSSVM模型参数时对应的收敛曲线，可以看出，PSO优化MK-LSSVM模型时在第336次迭代处收敛，而ACPSO优化MK-LSSVM模型时在305次迭代处收敛，并且ACPSO的收敛精度更高，在混沌扰动策略下，可以避免陷入局部极值，能够达到模型训练的误差精度要求范围，相较于PSO算法，其寻优速度更快且收敛精度更高，明显的提高了MKLSSVM模型的学习效率。

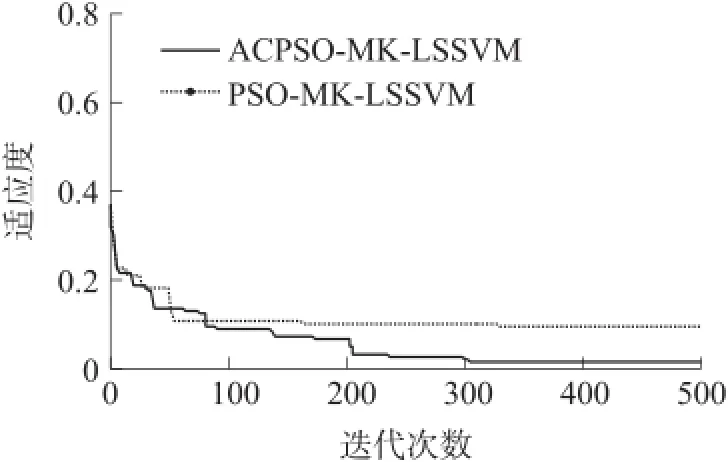
图3　适应度优化曲线

5.3试验结果分析

用已建立的动态预测模型，通过Matlab2012对样本471-500的瓦斯浓度值进行预测。瓦斯浓度百分比的真实值和预测值的对比如图4所示，从图4中可以分析得出，预测曲线与真实曲线之间的滞后性较小，预测结果与真实瓦斯浓度时间序列样本的缓慢变化趋势有良好的一致性。预测结果相对误差如图5所示，相对误差在-2.2%～2.1%之间，平均相对误差为仅1.43%，说明所建立的MK-LSSVM模型经过ACPSO优化以及误差校正后，具有更好的泛化能力，能够实现对瓦斯浓度的良好预测。

图4　瓦斯浓度预测值与真实值对比

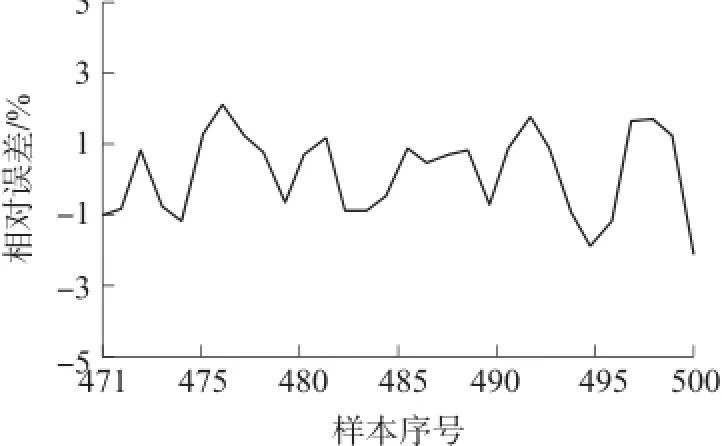
图5　预测相对误差

在同样的训练样本及参数设置条件下，分别用LSSVM、PSO-LSSVM两种模型和本文提出的MK-LSSVM动态预测模型对瓦斯浓度进行预测，并以平均绝对百分比误差（MAPE）、平均相对变动值（ARV）和相对均方根误差（RRMSE）作为衡量预测模型的泛化能力和预测精度的指标。将三种模型的预测效果进行分析对比，结果如表1所示。

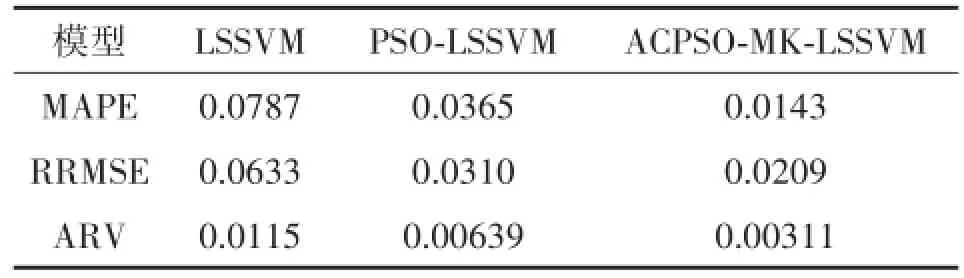
表13　种模型预测性能对比

从表1可知，与LSSVM和PSO-LSSVM两种预测模型相比，ACPSO优化的MK-LSSVM模型的误差指标最小。经过PSO算法优化的LSSVM模型其误差指标比直接用LSSVM模型预测的误差小，说明经过PSO优化后LSSVM模型的预测精度有所提高，但由于核函数单一并且PSO算法容易陷入局部极值，因此模型的性能仍然比ACPSO-MKLSSVM模型差，LSSVM和PSO-LSSVM模型的MAPE是0.078 7和0.036 5，而ACPSO-MK-LSSVM模型的MAPE值仅有0.014 3，说明该模型比另外两种预测模型有更好的适应能力；ACPSO优化和误差校正后，MK-LSSVM模型的RRMSE值为0.020 9，比前两种模型的值0.063 3和0.031 0都小，说明其具有更精准的预测精度；ACPSO-MK-LSSVM模型的ARV值0.003 11更反映出该模型具有更强的泛化能力。因此说明，该方法对工作面瓦斯浓度的预测比其他两种方法有更好的适应性，可以在满足是实际工程应用需要的同时，实现高精度、高效率的工作面瓦斯浓度的动态预测。

6　结束语

本文通过分析瓦斯浓度时间序列特性，重构具有全局核函数和局部核函数的MK-LSSVM模型，并提出ACPSO算法优化模型参数，提高了模型的泛化能力和学习能力。同时，实时滚动更新MK-LSS⁃VM预测模型的训练样本，使得预测系统能够反映瓦斯浓度的最新变化规律，并对预测值进行误差校正，提高系统的预测精度。利用基于ACPSO算法和PSR的MK-LSSVM动态预测方法对井下瓦斯浓度预测进行试验，结果表明，该方法具有较好的预测精度并且泛化能力较强，能够有效地实现对井下工作面瓦斯浓度趋势的预测。

［1］董丁稳，李树刚，常心坦，等.瓦斯浓度区间预测的灰色聚类与高斯过程模型［J］.中国安全科学学报，2011，21（5）：40-45.

［2］陈学习，宋富美，闫智婕.基于分形理论的瓦斯涌出规律［J］.辽宁工程技术大学（自然科学版），2012，31（5）：617-620.

［3］邵良杉，付贵祥.基于数据融合理论的煤矿瓦斯动态预测技术［J］.煤炭学报，2008，33（5）：551-555.

［4］付华，谢森，徐耀松，等.基于MPSO-WLS-SVM的矿井瓦斯涌出量预测模型研究［J］.中国安全科学学报，2013，23（5）：56-61.

［5］王其军，程久龙.基于免疫神经网络模型的瓦斯浓度智能预测［J］.煤炭学报，2008，33（6）：665-669.

［6］董丁稳，刘洁，王红刚.矿井瓦斯浓度自适应预测及其预警应用［J］.中国安全科学学报，2013，23（5）：88-93.

［7］Samanta B.Prediction of Chaotic Time Series Using Computation⁃al Intelligence［J］.Expert Systems with Applications，2011，38（9）：11406-11411.

［8］Gao Y，Li Y.Fault Prediction Model Based on Phase Space Re⁃construction and Least Squares Support Vector Machines［C］//Hy⁃brid Intelligent Systems，2009.HIS’09.Ninth International Con⁃ference on.IEEE，2009，3：464-467.

［9］付华，刘雨竹，李海霞，等.煤矿瓦斯浓度的CAPSO-ENN短期预测模型［J］.传感技术学报，2015，28（5）：717-722.

［10］Bi J，Zhang T，Bennett K P.Column-Generation Boosting Methods for Mixture of Kernels［C］//Proceedings of the Tenth ACM SIG⁃KDD International Conference on Knowledge Discovery and Data Mining.ACM，2004：521-526.

［11］Chen J，Yang H.Application of Mixture Kernels SVM in Chemi⁃cal Industry Soft Sensing［J］.Control and Instruments in Chemi⁃cal Industry，2008，35（2）：36.

［12］程健，白静宜，钱建生，等.基于混沌时间序列的煤矿瓦斯浓度短期预测［J］.中国矿业大学学报，2008，37（2）：231-235.

［13］张文超，谭思超，高璞珍.基于Lyapunov指数的摇摆条件下自然循环流动不稳定性混沌预测［J］.物理学报，2013，62（6）：61-68.

付华（1962-），女，辽宁阜新人，教授，博士生导师，博士（后），主要研究方向为煤矿瓦斯检测、智能检测和数据融合技术。主持国家自然科学基金2项、主持及参与国家863和省部级项目30余项，发表学术论文40余篇，申请专利24项，fxfuhua@163.com；

代巍（1984-），女，辽宁本溪人，辽宁工程技术大学，安全科学与工程学院，博士研究生，主要研究方向煤矿瓦斯安全监测监控，daiweihld@163.com。

EEACC：723010.3969/j.issn.1004-1699.2016.06.019

基于ACPSO的PSR-MK-LSSVM瓦斯浓度动态预测方法*

付华1*，代巍2
（1.辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛125105；2.辽宁工程技术大学安全科学与工程学院，辽宁阜新123000）

为了准确预测采煤工作面的瓦斯浓度，提出基于相空间重构理论、自适应混沌粒子群优化理论的混合核最小二乘支持向量机瓦斯浓度动态预测方法。以井下无线传感器网络监测系统采集到的工作面瓦斯浓度作为研究对象，通过平移不变小波降噪法滤除干扰瓦斯浓度的噪声，以相空间重构的瓦斯浓度序列样本训练混合核最小二乘支持向量机模型，利用自适应混沌粒子群算法优化模型参数，并通过误差校正的方法提高整体系统的预测精度。实验结果表明，提出的动态预测方法可以实现对工作面的瓦斯浓度的良好预测，平均相对误差MAPE值为0.024 1、相对均方根误差RRMSE值为0.209 7和平均相对变动ARV值0.003 11，预测结果合理并且满足工程的实际需要，可为煤矿瓦斯预测和防治工作提供有效理论依据。

瓦斯浓度；动态预测；相空间重构；自适应混沌粒子群；混合核最小二乘支持向量机

X936

A

1004-1699（2016）06-0903-06

2015-11-17修改日期：2016-01-31

项目来源：国家自然科学基金项目（51274118）