瓣形均匀带电面和均匀带电体在其球心处的电场

胡　冰　邓加军　李社强　王文杰（华北电力大学数理系，北京 102206）

瓣形均匀带电面和均匀带电体在其球心处的电场

胡冰邓加军李社强王文杰
（华北电力大学数理系，北京 102206）

在大学物理课程电磁学部分的教学中，经常会利用高斯定理研究均匀带电球面、均匀带电球体等电荷分布具有高度对称性的带电体的电场分布.对于这些均匀带电球面、均匀带电球体的一部分，比如瓣形均匀带电面和瓣形均匀带电体，利用高斯定理不能求出其电场分布，但是可以利用点电荷的电场强度公式加电场叠加原理的方法研究在一些特殊位置的电场.本文推导出了瓣形均匀带电面和瓣形均匀带电体在特殊点球心处的电场，并且进一步讨论了均匀带电半球面、球面、半球体和球体在球心处的电场.

瓣形均匀带电面；瓣形均匀带电体；电场；电场叠加原理

在大学物理课程电磁学部分的教学中经常会讨论均匀带电球面、均匀带电球体等电荷分布具有高度对称性的带电体的电场分布，一般教师讲解时是利用高斯定理求解［1，2］.对于这些均匀带电球面、均匀带电球体的一部分，比如瓣形均匀带电面和瓣形均匀带电体，利用高斯定理就不能求出其电场分布.其实也可以利用点电荷的电场强度公式加电场叠加原理的方法研究瓣形均匀带电面和瓣形均匀带电体在特殊点球心处的电场，进而可以获得均匀带电半球面、球面、半球体和球体在球心处的电场.

1　瓣形均匀带电面在其球心处的电场及讨论

1.1瓣形均匀带电面在其球心处的电场

图1所示的瓣形均匀带电面是球面的一部分，以球心为坐标原点建立如图所示的直角坐标系.瓣形带电面所在球面的半径是R，瓣形对z轴所张角度是φ，面电荷密度是σ.现在求球心O处的电场.

图1　瓣形均匀带电面

如图1所示，在瓣形带电面上任取一个小面元d S，据文献［3］面元的球面坐标是（R，φ，θ），且可知

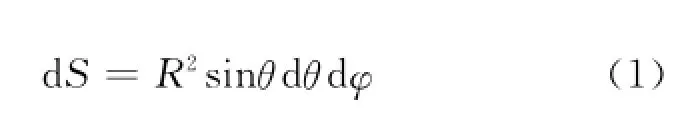
面元d S所带电量d q

根据点电荷的电场强度公式得到面元所带的电荷d q在球心O处产生的电场大小为

电场的方向是沿球的径向.把d q产生的电场d E 沿x，y，z轴进行分解得d Ex，d Ey，d Ez，则

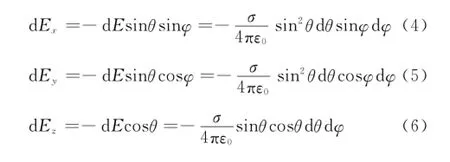
根据电场叠加原理，瓣形均匀带电面在球心处的电场分量是

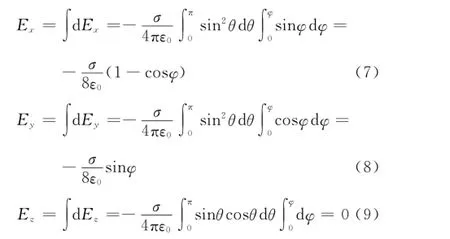
由以上结果可以看出，瓣形均匀带电面在球心处的电场没有沿z轴的分量，电场只在x Oy平面内.根据电荷分布的对称性也可以得到这个结论.所以瓣形均匀带电面在球心处的电场为

1.2均匀带电半球面在其球心处的电场

由瓣形均匀带电面在其球心处的电场可以讨论得到均匀带电半球面在球心处的电场，只需让φ=π，则

电场只是沿x轴的方向.根据电荷分布的对称性也可以分析得到球心处的电场只能沿x轴的方向.

1.3均匀带电球面在其球心处的电场

根据式（10）可得，当φ=2π时，

此时瓣形均匀带电面是一个球面，这时球心处的电场是零.根据对称性也可以分析得到均匀带电球面在球心处的电场为零.

2　瓣形均匀带电体在其球心处的电场及讨论

2.1瓣形均匀带电体在其球心处的电场

图2表示一个瓣形的均匀带电体，它是球体的一部分.瓣形带电体所在球体的半径是R，瓣形对z轴所张角度是φ，体电荷密度是p.现在求球心O处的电场.

在瓣形带电体上任取一个小体元d V，据文献［3］体元的球坐标是（r，φ，θ），且可知

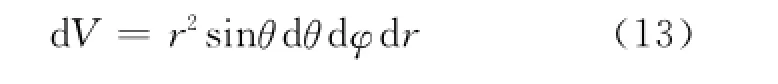
图2　瓣形均匀带电体

体元d V所带电量d q

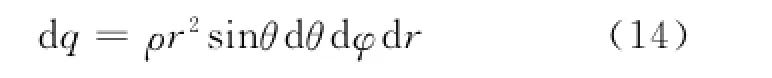
根据点电荷的电场强度公式得到体元所带的电荷d q在球心O处产生的电场大小

电场的方向是沿球的径向.把d q产生的电场d E 沿x，y，z轴进行分解得d Ex，d Ey，d Ez，有

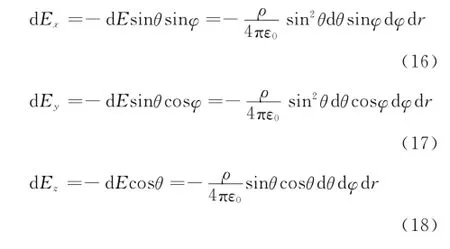
根据电场叠加原理，瓣形均匀带电体在球心处的电场分量是

由以上结果可以看出，瓣形均匀带电体在球心处的电场没有沿z轴的分量，电场只在x Oy平面内.根据电荷分布的对称性也可以得到这个结论.所以瓣形均匀带电体在球心处的电场为

把式（22）与式（10）进行比较发现，式（10）中的面电荷密度σ用体电荷密度p和球体半径R的乘积p R代替就变成式（22）.

2.2均匀带电半球体在其球心处的电场

由瓣形均匀带电体在其球心处的电场可以讨论得到均匀带电半球体在球心处的电场，只需让φ=π，则

电场只是沿x轴的方向.根据电荷分布的对称性也可以分析得到球心处的电场只能沿x轴的方向.

2.3均匀带电球体在其球心处的电场

根据式（22）可得，当φ=2π时，

此时瓣形均匀带电体是一个球体，这时球心处的电场是零.根据对称性也可以分析得到这个结论.

3　结语

本文先是利用电场叠加原理推导出瓣形均匀带电面在其球心处的电场.利用所得的结果讨论了均匀带电半球面和球面在球心处的电场.然后推导出瓣形均匀带电体在其球心处的电场，并讨论了均匀带电半球体和球体在球心处的电场.最后发现在瓣形均匀带电面球心处电场的表达式中，面电荷密度σ代换成p R（p是体电荷密度，R是球体半径），表达式就变成瓣形均匀带电体在球心处的电场表达式.

［1］ 程守洙，江之永.普通物理学2［M］.北京：高等教育出版社，1998.

［2］ 张三慧.大学物理学电磁学［M］.北京：清华大学出版社，1999.

［3］ 四川大学数学系高等数学教研室.高等数学2［M］.北京：高等教育出版社，1996.

ELECTRIC FIELD AT THE CENTER OF UNIFORMLY CHARGED PETAL-LIKE SURFACE AND UNIFORMLY CHARGED PETAL-LIKE BODY

Hu Bing Deng JiajunLi Sheqiang Wang Wenjie
（Department of Mathematics and Physics，North China Electric Power University，Beijing 102206）

As a part of electromagnetism teaching in the college physics course，Gauss，s law is usually applied on the solution of electric fields of the uniformly charged spherical surface and uniformly charged sphere，which are charged bodies with high symmetry in charge distribution.But Gauss，s law cannot be used to solve the electric fields of a part of the uniformly charged spherical surface or a part of the uniformly charged sphere，such as an uniformly charged petal-like surface or an uniformly charged petal-like body.However，the electric field superposition principle of point charges can be used to study the electric fields at some special position.In this paper，electric field at the center of uniformly charged petal-like surface and uniformly charged petal-like body are calculated by means of the electric field superposition principle.Furthermore，the electric fields at the center of uniformly charged hemispherical surface，spherical surface，hemisphere and sphere are discussed.

uniformly charged petal-like surface；uniformly charged petal-like body；electric field；superposition principle of electric field

2015-01-27；

2015-10-24

2014年北京市高等学校教育教学改革立项（2014-ms114）；华北电力大学中央高校基本科研业务费（JB2014106）.

胡冰，女，讲师，主要从事物理教学科研工作，研究方向为低维半导体材料.bhu@ncepu.edu.cn