基础阶段几类分式方程的常见解法
☉湖北省恩施土家族苗族自治州高级中学 刘芃德
基础阶段几类分式方程的常见解法
☉湖北省恩施土家族苗族自治州高级中学刘芃德
在基础教育阶段,解方程的思想主要是:高次降次、多元消元、分式方程整式化、无理方程有理化.在初中阶段,分母里含有未知数的方程叫作分式方程.其中解分式方程的基本思想是整式化,因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根(使得最简公分母为0的未知数的值我们称之为增根),所以在求出未知数的值后必须验根.
分式方程的具体解法的步骤为:
(1)去分母(方程两边同时乘以最简公分母,将分式方程化为整式方程);
(2)按解整式方程的步骤求出未知数的值;
(3)验根,把整式方程的根代入最简公分母,如果最简公分母等于0,这个根就是增根.否则这个根就是原分式方程的根.
解分式方程常见的方法有:常规方法、换元法、因式分解法、部分分式法、通分或整体通分法、分离常数法等.
则四边形CGEB是垂美四边形,
由(2)得:CG2+BE2=CB2+GE2.
则GE2=CG2+BE2-CB2=73.则GE=
【溯源】八年级上册P53活动2用全等三角形研究“筝形”,本题是在本活动的基础上通过一般化与拓展应用,把活动与问题链接起来,形成了一道迁移性较好的题目.
【赏析】本题是一道数学味浓郁的几何题,首先通过一句精炼的现场性定义,然后设置三个台阶“概念理解—性质探究(猜想与证明)—问题解决”,步步深入,把三种语言(文字语言、符号语言、图形语言)的转换,合情推理与逻辑推理(结论的猜想与证明)的结合,以及结论的迁移性应用融为一体,成为考查图形核心知识、技能及推理等综合素养的好题目.其中(1)根据垂直平分线的判定定理证明即可;(2)根据垂直的定义和勾股定理解答即可;(3)根据获得的垂美四边形的性质、勾股定理,结合(2)的结论计算即得.三个问题一脉相承,关联密切,是基于教材、高于教材的创新题.
以上各题的背景材料直接取自于教材,但通过命题专家的适度改造与创新,成为一道道靓丽的风景,同时成为中考场上能力立意的好题目,既有效考量了考生,又给了我们教学的优质素材,探研之余享受到题目带来的愉悦,有余味悠长之感,这正是我们期盼的命题方向.
一、常规方法解分式方程
分析:此题用分式方程一般的解法就可以,两个分母分别为x,x+3,所以它们的最简公分母M=x(x+3),分式方程的两边同时乘以最简公分母M即可化为整式方程.
解:将分式方程的两边同时乘以M=x(x+3),可得2(x+3)+x2=x(x+3),可得整理可得x-6=0,解得x=6.
检验:当x=6时,M=x(x+3)=18≠0,故x=6是原分式方程的解.
二、分离常数法解分式方程
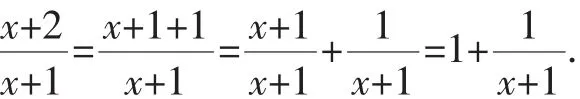
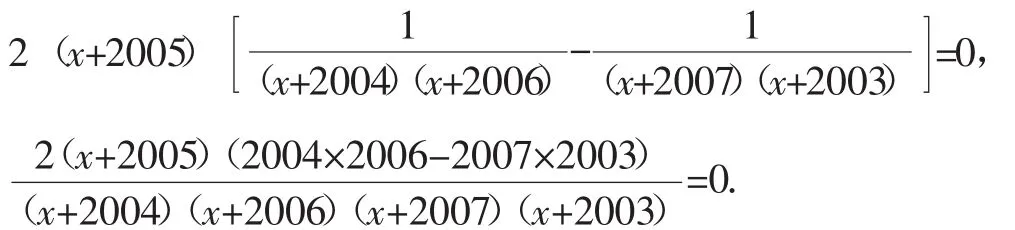
将方程两边同时乘以(x+2004)(x+2006)(x+2007)· (x+2003),可得2(x+2005)(2004×2006-2007×2003)=0.
因为2004×2006-2007×2003≠0,所以x+2005=0,得x=-2005.
检验:当x=-2005时,因为(x+2004)(x+2006)(x+ 2007)(x+2003)≠0,所以x=-2005是原分式方程的解.
三、裂项相消法解分式方程
裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到简化求和的目的.裂项相消法在求解分式方程中主要是将每一项裂成两项,达到相关运算消除从而简化求和运算.
分析:首先仔细观察分式方程的特征,分母都是两个一次式之积,并且它们之间的差都是1,而分子正好是1,所以可以裂项相消,裂项是手段,而相互抵消是目的.
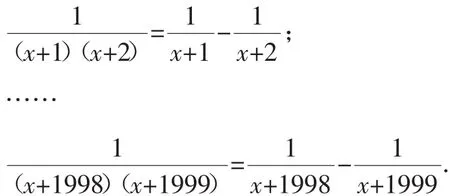
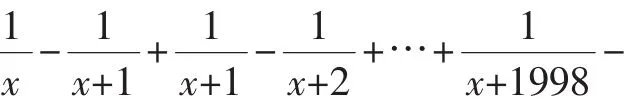
分析:此题用分式方程一般的解法就可以,两个分母分别为x2-1与x-1,所以它们的最简公分母M=x2-1,分式方程的两边同时乘以最简公分母M即可化为整式方程.
解:将分式方程的两边同时乘以最简公分母M=x2-1,可得6-3(x+1)=x2-1,整理可得x2+3x-4=0,解得x1=-1,x2=4.
检验:当x=-1时,M=x2-1=0,所以x=-1是增根,不合题意,舍去;当x=4时,M=x2-1≠0,所以x=4是原分式方程的解.
综上所述:x=4是原分式方程的解.
将方程两边同时乘以(x+1999),可得x+1999=-1,解得x=-2000.
检验:当x=-2000时,因为(x+1999)≠0,所以x=-2000是原分式方程的解.
注:如果分子不是1,而是其他的常数a(a≠1),那么这种方法依然可行.
四、取倒数解分式方程
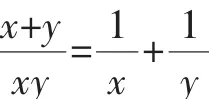
解:对这三个方程先取倒数,可得:
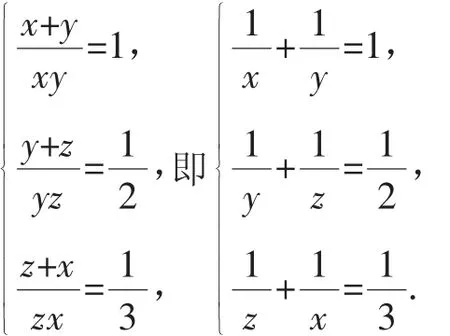
五、换元法解分式方程
换元法就是用一个简单的字母去代表相同的较为复杂的代数式,从而达到简化的目的,用换元法的时候一定要注意还原,将引入的某些字母参量还原成与题目有关的参量.
分析:观察方程分母是三个二次式,x2+11x-8,x2+ 2x-8,x2-13x-8,不难发现这三个二次式都含有相同部分x2-8,则可用换元法来解方程,两种不同的换元形式,x2-8=a,x2-13x-8=a,两种不同的换元形式我们都看一下.
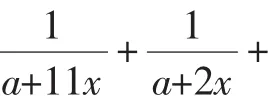
检验:当x=±1或x=±8时,因为(x2+11x-8)(x2+2x-8)· (x2-13x-8)≠0,所以x=±1,x=±8是原分式方程的解.
检验:当x=±1或x=±8时,因为(x2+11x-8)(x2+2x-8)· (x2-13x-8)≠0,所以x=±1,x=±8是原分式方程的解.
解法一和解法二虽然在换元的处理方法上略有不同,但是殊途同归.
以上是基础教育阶段几种分式方程的典型解法,相信只要认真分析每个分式方程所属类型和找寻它们内在的联系与规律,通过适当的方法,再难的分式方程都能够迎刃而解.

