牵手“面积函数”的四边形压轴题
☉河南省商水县平店乡第一初级中学 支永辉
牵手“面积函数”的四边形压轴题
☉河南省商水县平店乡第一初级中学支永辉
近年来的中考打破了坐标系与圆联手坐阵中考压轴题的格局,出现了“一枝独秀不是春,万紫千红春满园”这种百花竞放的新景观,其中很难占据压轴位置的四边形悄然牵手“面积函数”(以求面积为目标的函数,为表述方便,在此自设的特定称谓),博得压轴的一席之位,给“把关题”带来了活力.现择几道近几年的中考题作一盘点,以飨读者.
一、矩形牵手“面积函数”
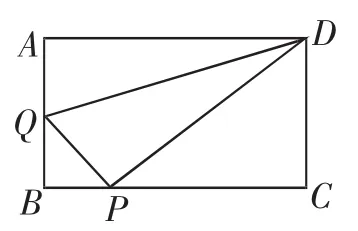
图1
例1(2016年宁夏)如图1,在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题:
(1)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最大值?并求出最小值.
(2)是否存在x的值,使得QP⊥DP?试说明理由.
分析:本题为四边形的综合应用,涉及的知识点有矩形的性质、二次函数的最值、相似三角形的判定和性质及方程思想等.在(1)中求得S关于x的关系式(面积函数)后,求S的最值时,x的取值范围尤为重要,不谨慎就会出错;在(2)中寻出三角形相似并证明其相似是解题的关键.这种探索性追溯是近来中考中常见的题类,值得我们关注.(1)可用x表示出AQ、BQ、BP、CP,从而可表示出S△ADQ、S△BPQ、S△PCD的面积,则可表示出S,再利用二次函数的增减性可求得是否有最大值,并能求得其最小值;(2)用x表示出BQ、BP、PC,当QP⊥DP时,可证明△BPQ∽△CDP,利用相似三角形的性质可得到关于x的方程,可求得x的值.
解:(1)因为四边形ABCD为矩形,所以BC=AD=4,CD=AB=3.
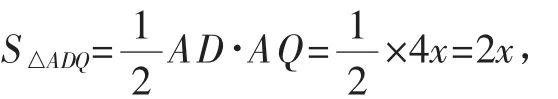
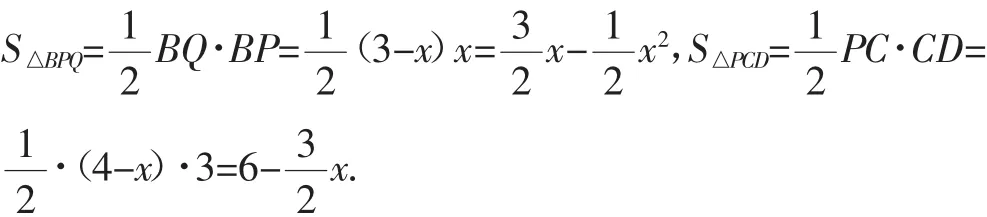
又S矩形ABCD=AB·BC=3×4=12,所以S=S矩形ABCD-S△ADQ-
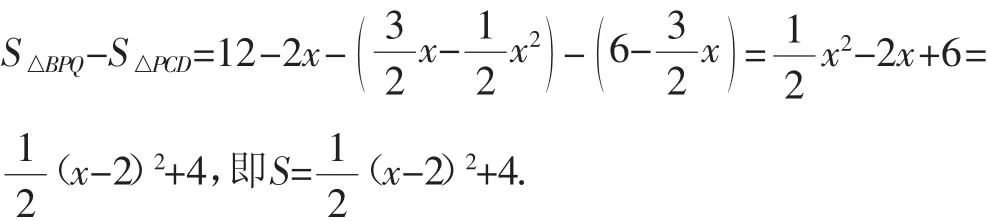
所以S为开口向上的二次函数,且对称轴为x=2.
所以当0<x<2时,S随x的增大而减小,当2<x≤3时,S随x的增大而增大.
(2)存在,理由如下:
由(1)可知,BQ=3-x,BP=x,CP=4-x.
当QP⊥DP时,则∠BPQ+∠DPC=∠DPC+∠PDC.
所以∠BPQ=∠PDC,且∠B=∠C.
所以△BPQ∽△PCD.
二、正方形牵手“面积函数”
例2(2016年广东)如图2,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明.
(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.

图2
分析:三个问题形成关联,第(1)、(2)问为第(3)问提供了数量及位置的关系,既然是求三角形的面积,自然离不开高线,这样以来辅助高可谓呼之欲出.(1)、(2)略;(3)需要分类讨论的支持,然后借力辅助线获得两个不同的面积函数,这样,在最后最大值的确定上就需要比对选择.
解:(1)四边形APQD为平行四边形.(过程略)
(2)OA=OP,OA⊥OP,理由如下:
因为四边形ABCD是正方形,所以AB=BC=PQ,∠ABO=∠OBQ=45°.
因为OQ⊥BD,所以∠PQO=45°,所以∠ABO= ∠OBQ=∠PQO=45°.
所以OB=OQ,所以△AOB≌△OPQ.
所以OA=OP,∠AOB=∠POQ.
所以∠AOP=∠BOQ=90°.
所以OA⊥OP.
(3)过点O作OE⊥BC于点E.
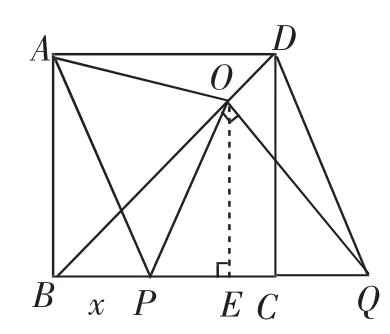
图3
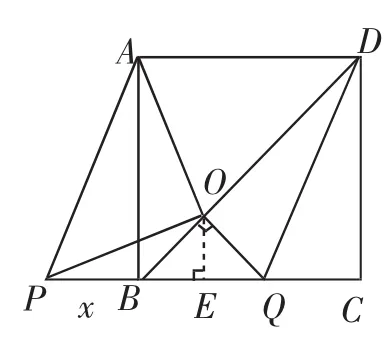
图4
又0≤x≤2,所以当x=2时,y有最大值为2.
综上所述,当x=2时,y有最大值为2.
三、平行四边形牵手“面积函数”
例3(2007年长沙)如图5,在▱ABCD中,AB=4,BC=3,∠BAD=120°,E为BC上一动点(不与B重合),作EF⊥AB于点F,FE、DC的延长线交于点G,设BE=x,△DEF的面积为S.
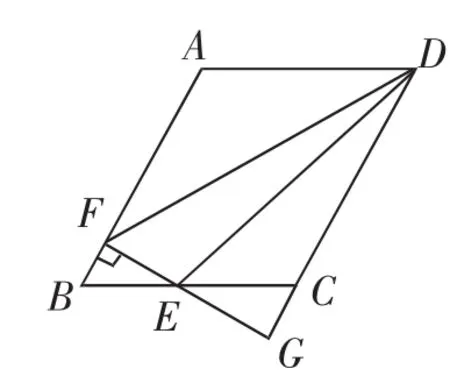
图5
(1)求证:△BEF∽△CEG;
(2)求用x表示S的函数表达式,并写出x的取值范围;
(3)当E运动到何处时,S有最大值,最大值为多少?
分析:本题通过一个简单的相似证明揭开序幕,然后仍然聚焦“面积与函数、取值范围及运动中的最大(小)”问题,所不同的是本题需要三角函数的支持,并且最大(小)值不能在顶点处取得,需要灵活使用函数的增减性做出选择,这显然是一个美丽的陷阱!
解:(1)证明略.
(2)由(1)得DG为△DEF中EF边上的高.
所以,当x=3,即点E与点C重合时,S有最大值,S最大=
四、菱形牵手“面积函数”
例4(2016年长春)如图6,在菱形ABCD中,对角线AC与BD相交于点O,AB=8,∠BAD=60°.点E从点A出发,沿AB以每秒2个单位长度的速度向终点B运动.当点E不与点A重合时,过点E作EF⊥AD于点F,作EG∥AD交AC于点G,过点G作GH⊥AD交AD(或AD的延长线)于点H,得到矩形EFGH.设点E运动的时间为t秒.
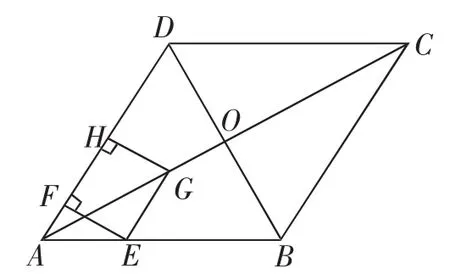
图6
(1)求线段EF的长.(用含t的代数式表示)
(2)求点H与点D重合时t的值.
(3)设矩形EFHG与菱形ABCD重叠部分图形的面积为S,求S与t之间的函数关系式.
(4)矩形EFHG的对角线EH与FG相交于点O′.当OO′∥AD时,t的值为______;当OO′⊥AD时,t的值为______.
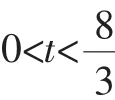
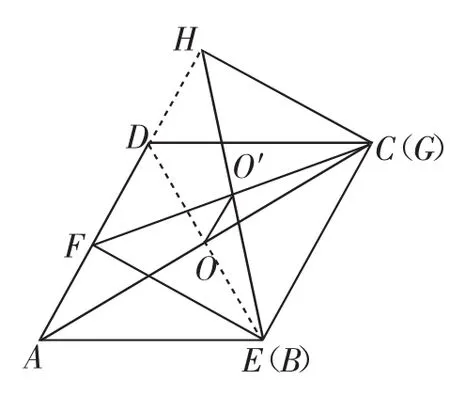
图7

图8
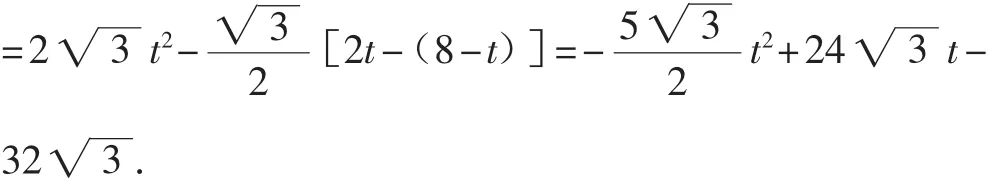
(4)t=4;t=3.(矩形EFHG的对角线EH与FG相交于点O′,当OO′∥AD时,如图7,点O与点O′为所在线段中点,t的值为4;当OO′⊥AD时,如图8,有AF+FM+MD=t+t+2= 8,t=3)
纵观以上不难发现,这类题目以特殊四边形作载体,融入新课程标准所关注的动的理念,在其上设置了点的运动,并在运动中探索以“面积为本”的函数关系,进而寻得最大或最小值,其中需要函数、相似、三角函数、方程等核心知识,以及数形结合、分类讨论、方程等思想方法的鼎力相助,它们在四边形的平台上各显神通,成为中考的亮点之一.

