多元方法在初中数学解题中的应用
☉江苏省张家港市护漕港中学 孙 彪
多元方法在初中数学解题中的应用
☉江苏省张家港市护漕港中学孙彪
解决初中数学难题可以采用丰富多样的解决方法,在解决不同的数学问题中要灵活采用多元解题方法,从而确保解题效率和质量的提升.在解决数学问题时,首先需要对问题中涉及的知识进行观点的提炼,接下来有效地将观点转化为方法,根据解题的需要选择恰当的解决办法,进行数学解题方法的总结和调整,通过不断的经验总结和深入学习,知识迁移能力也会得到很大程度的提升,这样在初中数学解题中也会更加得心应手.
一、消去法
在解决初中数学问题时,经常会遇到两种及其以上未知的相关数量关系,在解答这类数学问题时可以通过适当的变换设法消去某些数量关系和相关元素,从而快速解决问题,这种解题方法就是消去法,消去法在应用过程中可以是代入消去或者加减消去.利用消去法解决初中数学难题的关键在于设法将未知数量变少,通过适当的变化消去具有一定关联的数量关系,从而使原本复杂的问题变得简单.
例1小明买产品,有两种买的方案:买A产品1个,B产品3个,C产品4个,D产品5个,E产品6个,这种方案要花1876元;买A产品1个,B产品5个,C产品7个,D产品9个,E产品11个,这种方案要花2984元,求每种产品各多少元(不用方程解)?
试题解析:在看到这一数学题目之后,如果不深入分析可以采用的解题方法肯定会被题目中大量的数量关系难住,从而阻碍解题的步伐.首先,对这一题目进行分析之后能够发现,在这个题目当中蕴含着多种数量关系,并且它们是相互关联的,因此在解题时可以通过适当的变换减少数量关系,这时就可以应用消去法.其次,对每一种方案进行相应的列式计算后得到方案一:A+ 3B+4C+5D+6E=1876(元);方案二:A+5B+7C+9D+11E= 2984(元),采用加减消去法,方案二减去方案一得到2B+ 3C+4D+5E=1108(元),方案一再减去上式得A+B+C+D+ E=768(元),则B=768-A-C-D-E,代入第一种方法得428+C+2D+3E=2A化掉了B,同理逐步化掉其他字母得出其一,全题可解.
二、配方法
配方法在初中数学解题中具有广泛的应用,但实际应用中往往是将不构成完全平方公式的多项式通过拆项、添项的方法,将原来多项式中的一部分构成一个能够应用公式进行解决的完全平方公式,从而提高解题效率.配方法在一元二次方程的解决当中应用最为广泛,其一般步骤是:第一,将方程的两边同时除以本方程的二次项系数,将系数化为1;第二,采用移项的方法将方程的右边只剩下常数项,左边是一次项及二次项;第三,进行配方,即方程的两边同时加上左边一次项系数一半的平方,将其变成一个完全平方公式;第四,分情况讨论,如果常数项大于或者等于零,那么可以直接采用开平方法解出答案,反之,则证明原方程无解.配方法对于解决数学问题非常重要,不仅仅能够用于解决一元二次方程的问题,还广泛应用在其他领域.
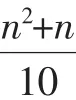
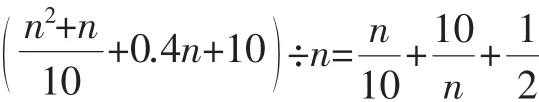
例3分解因式:x4+4.
试题解析:x4+4=x4+4x2+4-4x2=(x2+2)2-4x2=(x2+2x+ 2)(x2-2x+2).
以上解法中,在x4+4的中间加上一项,使得三项组成一个完全平方式,为了使这个式子的值与x4+4的值保持不变,必须减去同样的一项.由此可知,配方法在因式分解当中的应用.
例4若三角形的三边长是a,b,c,且满足a2+2b2+c2-2ab-2bc=0,试判断三角形的形状.
试题解析:因为a2+2b2+c2-2ab-2bc=0,所以(a2-2ab+ b2)+(b2-2bc+c2)=0,即(a-b)2+(b-c)2=0.因为(a-b)2≥0,(b-c)2≥0,所以a=b,b=c,即a=b=c.故该三角形是等边三角形.在借助配方法后,能够轻松判定集合图形的形状,可见配方法应用之广.
三、换元法
解数学题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,叫作换元法.通俗的说,换元法就是把一个括号里的式子换成和题目中的字母不同的任何字母.换元法的应用条件为:式子比较复杂;一个整体多次出现;另外的未知数能用这个整体来表示.换元法能够将原本复杂的数学问题变得简单,同时也是转化思想在初中数学解题当中的应用,在数学解题中运用换元法能够锻炼数学思维,突破数学解题当中题目过长或者数量关系过多的难题.
例5已知(x2-1)2-5(x2-1)+4=0,求未知数x.
例题解析:为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1看作一个整体,设x2-1=y①,那么原方程可化为y2-5y+4=0,解得y1=1,y2=4,当y=1时,x2-1=1,即x2=2,解得x=±;当y=4时,x2-1=4,即x2=5,解得x=±,故原方程的解为以上解题方法叫作换元法,在由原方程得到方程①的过程中,利用换元法达到了解方程的目的,在使用换元法之后,原本复杂的解题步骤能够得到化解,在今后解决类似问题的过程中也会得心应手.
例6(x2+x)2+(x2+x)=6,求未知数x.
例题解析:在解决这一方程问题时同样也会用到换元法,(x2+x)2+(x2+x)=6,可以设x2+x=y,则原方程可化为y2+y=6,解得y1=-3(舍去),y2=2,当y=2时,x2+x=2,解得x1=-2,x2=1,所以原方程的解为x1=-2,x2=1.在解决这一问题时涉及了分类讨论的方法,因为一个数的平方是大于或等于0的,所以得到的第一个解为负数就需要将其舍去,那么这个问题就得到了两个解,而不是四个.
四、待定系数法
待定系数法是一种求解未知数的有效方法,运用这一方法解题主要是通过将一个多项式用另一种含有特定系数的式子表示出来,因此会得到恒等式,按照恒等式的性质得到一个能满足方程或者方程组的系数,通过解方程组或者方程得到的数值就是待定系数的数值.在数学解题中应用待定系数法,可以按照以下几个步骤进行:写出函数解析式的一般式,其中包括未知的系数;根据恒等条件,将变量和函数的对应值代入到整个函数解析式当中,进而得到一个能够表示待定系数的方程或者方程组;通过求解方程或者方程组得到待定系数的数值,从而解决问题.待定系数法在函数知识学习中应用较多,主要用在求解函数解析式上,更是成为解决函数相关例题的好帮手.
例7已知一次函数图像经过点A(3,5)和点B(-4,-9)两点.
(1)求此一次函数的解析式;
(2)若点(a,2)在该函数的图像上,试求a的值;
(3)若此一次函数的图像与x轴交于点C,点P(m,n)是图像上一个动点(不与点C重合),设△POC的面积是S,试求S关于m的函数关系式.
例题解析:运用待定系数法首先求得函数解析式,接下来的求解只要围绕解析式来计算就会变得简便.
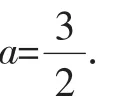
五、反证法
反证法在初中数学证明题当中应用较多,是一种间接证明的方法,而且很多数学命题只能够用反证方法去证明.反证法首先提出与给定命题相反的结论,接下来按照这个假设进行逐步推理,推理过程中如果出现矛盾,那么就可以否定做出的相反的假设,从而证明了原命题的正确性.在初中数学采用反证法证明命题的过程中会经历这样的思维变化:假定给出的结论不成立,那么就会导致出现这个问题和给出的已知条件自相矛盾,同时也和数学当中的公式和定理不符合.接下来就要讨论这一矛盾和问题存在的根源,整个数学推理的过程没有存在错误,题目给出的已知条件及数学中的公式定理都没有错误,那么在命题的证明中存在错误的地方只可能是刚开始的假设结论不成立,那么这一命题成立或者不成立只有一个是正确的结论,那么给出的否定结论不正确,则证明原命题的结论是成立的.通过反证法在初中数学解题中的应用能够锻炼辩证思维,从而在今后的解题中也会注重思维的灵活性和多样性,及时根据给定问题,选择恰当的解题方法.
例8请用反证法证明:如果两个整数的积是偶数,那么这两个整数中至少有一个是偶数.
例题解析:首先假设这两个整数都是奇数,其中一个奇数为2n+1,另一个奇数为2p+1,利用多项式乘以多项式得出(2n+1)(2p+1)=2(2np+n+p)+1,进而得出矛盾,则原命题正确.
证明:假设这两个整数都是奇数,其中一个奇数为2n+1,另一个奇数为2p+1(n、p为整数),则(2n+1)(2p+1) =2(2np+n+p)+1,因为无论n、p取何值,2(2np+n+p)+1都是奇数,这与已知中两个奇数的乘积为偶数相矛盾,所以假设不成立,故这两个整数中至少一个是偶数.
六、面积法
平面几何在初中数学知识体系当中占有很大的成分,平面几何当中涉及了不同图形面积计算及面积公式推理等方面的内容,它们不仅能够应用到解决面积计算的问题当中,还能用于平面几何题目的证明.因此,面积法是解决几何问题的常用方法,主要采用面积关系进行平面几何题目的证明及计算.在解决平面几何题时往往也采用分析法及归纳法,但是使用这些方法解题时会在添加辅助线上出现较大的困难.如果在解决这些问题时采用面积法则能够灵活地将未知量和已知量用面积公式结合起来,采用运算的方式求证结果.因此,将面积法应用到解决几何问题当中能够将几何元素之间的关联变成数量关系,从而能够巧妙地通过计算的方式无需添置辅助线就能够解决几何问题.
例9如图1所示,这是美国第20任总统加菲尔德证明勾股定理时所采用的图形,是用两个全等的直角三角形和一个等腰直角三角形拼出一个梯形.借助这个图形,你能用面积法来验证勾股定理吗?
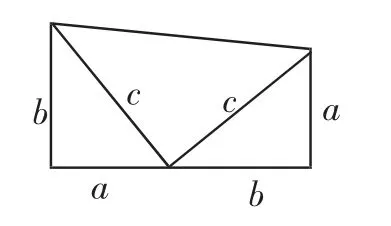
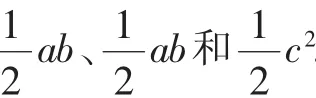
解决初中数学问题的方法是多种多样的,在应用相应的数学解题方法之前必须对问题进行深入分析,确定问题中蕴含的知识内容和观点,将复杂的问题简化为原则,进行多样化数学方法的应用.多元解题方法需要在不断的解题和知识应用当中进行归纳总结,同时也需要一双善于发现的眼睛和勇于探究的大脑,在今后的解题中笔者一定会再接再厉,善于观察和思考,将总结的多元解题方法应用到解决实际问题当中.

