巧思妙想 化“圆”为“方”

☉江苏盐城市尚庄初级中学　刘志才☉江苏盐城市葛武初级中学　王云峰☉江苏盐城市尚庄初级中学　王寿云

巧思妙想化“圆”为“方”

☉江苏盐城市尚庄初级中学刘志才
☉江苏盐城市葛武初级中学王云峰
☉江苏盐城市尚庄初级中学王寿云

一、引入议题

如何作一个正方形，使其面积等于已知圆的面积？

如图1，假定正方形ABCD已经作出，满足S正方形ABCD=S⊙O.

图1

设正方形ABCD的边长为a，⊙O的半径为R，必有a2= πR2.

二、联想构思巧变换

由a2=πR2容易联想到圆的切割线定理，于是将a2= πR2变形为a2=R·πR，进而变形为a2=R·C，其中C为圆周长.可见，求出半圆的周长是解决问题的关键所在.

三、化“曲”为“直”以求解

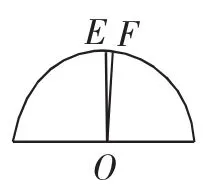
图2

在这里，我们有必要对直线和曲线的认识重新作一番解释，实质上，这个世界上不存在真正意义上的直线，换一个角度说，直线与曲线是存在于同一事物中的两个矛盾对立的统一体.曲线是直线之母，没有曲线，直线就不复存在，一条曲线是由若干条连贯的直线组合而成的.因此我们把曲线中的极小部分称为直线，所谓直线曲中求就是这个道理.判断直线的标准就是：显得较为扁平、平滑的曲线是直线.因此，当我们将一个半圆分成2n等份（n为自然数，n≥5）后，随着我们对n的取值的逐步增大（如图2），夹在相邻两半径之间的弧EF就显得越扁平、平滑，但为了能够获得较为清晰的几何作图痕迹，一般取n=5即可.（对精确度要求不是十分苛求的情况下采用）但随着对精确度要求的提高，n的值可逐步加大到一定的程度，但圆的半径的取值也要随之加大，以便于操作和获得清晰的几何作图痕迹为原则.以线段EF的长取代于弧EF的长，能否取代，主要的判断标准是看曲线EF是否已被直线化，在这里还需要强调一点，这时线段EF就是弧EF的本身，所以真正意义上线段是不存在的.设EF=b，从而求出半圆的长32b（当n=5时）.

四、相关证明得结论

1.相关理论证明

在2n（n为自然数，n≥5）中，当n趋向于无穷大时，这时夹在相邻两半径之间的弧EF的长趋向于零，线段EF的长亦趋向于零.这时我们说弧EF的长等于线段EF的长，所以我们以线段EF的长取代于弧EF的长成立.

2.相关实验证明

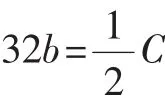
之间的误差分别是不足4忽米、不足4丝米和不足4毫米，有兴趣的朋友不妨验证一下.从而得出结论：当n=5时，即将半圆32等分后，夹在相邻两半径之间的曲线EF已经开始直线化.

五、作图实例

图3

如图3，已知⊙O.

求作：正方形ABCD，使S正方形ABCD= S⊙O.

作法：（1）将已知半圆32等分，得一等份的弧EF；

（2）视弧EF为线段，并设EF=b，在射线AL上截取AG=32b=C（C为⊙O的周长）；

（3）在AG上截取AH=R；

（4）以HG为直径画⊙O′；

（5）以AO′为直径画半圆O″，与⊙O′相交于点B，连接AB；

（6）以AB为一边作正方形ABCD.

如图4，则正方形ABCD为所求.

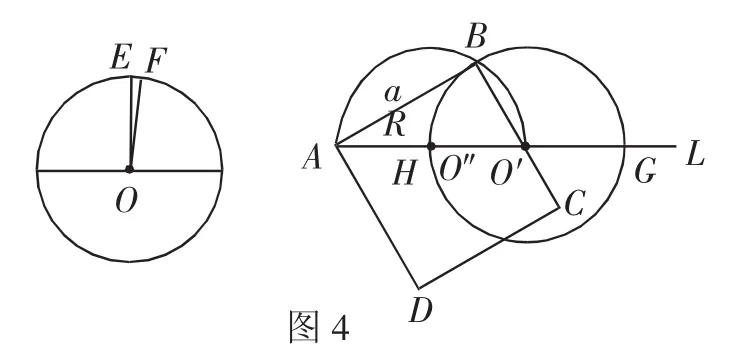
图4

证明：连接O′B，则O′B⊥AB，所以AB为⊙O′的切线. 设AB=a，因为AH=R，AG=C=πR，据圆的切割线定理知：a2=R·πR=πR2，即S正方形ABCD=S⊙O成立.