拉格朗日中值定理在定积分计算中的妙用
刘灯明
(湖南科技大学 数学与计算科学学院,湖南 湘潭 411201)
拉格朗日中值定理在定积分计算中的妙用
刘灯明
(湖南科技大学 数学与计算科学学院,湖南 湘潭 411201)
利用定义计算定积分时,若采用常规方法来分割积分区间和选取介点集,会使得积分和式的极限过程十分复杂。通过拉格朗日中值定理巧妙地选取中值点作为介点,可以简化积分和式的极限过程,从而简洁地得到计算结果。同时,利用拉格朗日中值定理,也可从另一角度推导出牛顿-莱布尼茨公式,从而将微分学中的微分中值定理和积分学中的微积分基本公式有机地结合起来。
拉格朗日中值定理;定积分计算;牛顿-莱布尼茨公式
拉格朗日中值定理是一元函数微分学中的一个重要内容,它深刻地反映了函数在某区间上的整体性质与函数在该区间上某点处的导数之间的关系。因此,拉格朗日中值定理在《数学分析》课程教学中的应用十分广泛,比如,通过构造合适的辅助函数,借助拉格朗日中值定理,我们可以方便快捷地证明一些不等式或恒等式、根的存在性问题、复杂级数的敛散性问题及某些复杂函数的极限[1-3]。本文通过具体例子来说明拉格朗日中值定理在定积分教学中的一个巧妙应用。
1 利用拉格朗日中值定理计算定积分
定积分是数学分析课程中除微分学外的另一核心内容。在整个定积分的教学过程中,定积分的计算是让许多初学者都感到困惑的难点。事实上,计算定积分的主要工具就是定积分的定义和牛顿-莱布尼茨公式。我们知道,若f为区间[a,b]上的可积函数,则对积分区间的任意分割与介点集{ξi}的自由选取都不会影响到积分值。基于此,在利用定积分的定义计算定积分时候,我们都是对[a,b]采取特殊的分割T(通常采取等分积分区间),并选取特殊的介点集{ξi}(通常取每一小区间的左端点或右端点)来构造积分和,最后再求积分和的极限。




由不等式

有

从而有

及



另一方面,有
an=b2n-bn+ln2n-lnn=b2n-bn+ln2。
故
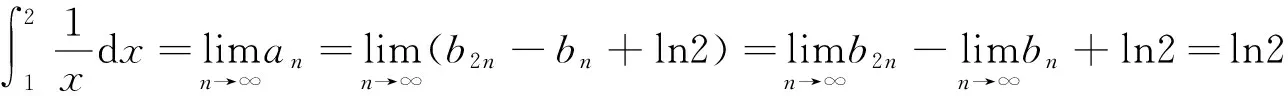

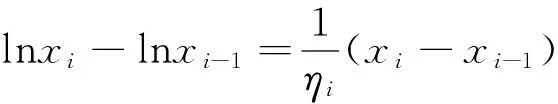
选取介点ξi=ηi,则有

(1)
解法二并没有具体的给出介点集,而是先对F(x)=lnx在每一小区间[xi-1,xi]上运用拉格朗日中值定理,再选取拉格朗日中值点作为介点。较之解法一,解法二容易理解,且避开了复杂的极限过程,整个计算显得十分简洁和方便。
2 结语
若被积函数在积分区间上连续且其原函数容易求出时,可以采取解法二中的处理手法来选择介点集。事实上,从(1)式可以看出,解法二本质上还是将定积分的计算转化为计算原函数在积分区间上的增量。故只需将解法二的表述更一般化,就可作为牛顿-莱布尼茨公式教学的一个新的引入。换句话说,从用定义计算定积分出发,利用拉格朗日中值定理,就可以得到一个异于文献[4-5]的牛顿-莱布尼茨公式的推导。可见,在数学分析课程教学过程中,完全可以将拉格朗日中值定理和定积分有机地结合起来,加深学生对相关内容的理解和掌握。
[1] 石业娇.谈拉格朗日中值定理在高等数学课程教学中的应用[J].常州信息职业技术学院学报,2014(13):26-28.
[2] 郑攀,胡学刚,李玲.关于拉格朗日中值定理在证明题中的一些应用[J].科教文汇,2015(6):59-60.
[3] 裘兆泰,王承国,章仰文.数学分析学习指导[M].北京:科学出版社,2004.
[4] 陈传璋,金福临,朱学炎,等.数学分析(上册)[M].北京:高等教育出版社,2010.
[5] 汤四平,吕胜祥,赵雨清.高等数学(上册)[M].北京:人民邮电出版社,2015.
(责任校对朱正余)
10.13582/j.cnki.1674-5884.2016.07.014
20160105
2015年湖南科技大学教学研究与改革一般项目(G31515)
刘灯明(1984-),男,湖南隆回人,讲师,博士,主要从事非线性偏微分方程的研究。
G642.0
A
1674-5884(2016)07-0043-02

