关联深度自适应的多假设跟踪研究
陈 杭, 张伯彦, 陈 映
(北京无线电测量研究所, 北京 100854)
关联深度自适应的多假设跟踪研究
陈杭, 张伯彦, 陈映
(北京无线电测量研究所, 北京 100854)
多假设跟踪(multiple hypothesis tracking, MHT)方法是一种在多个扫描上评价关联假设并由此做出决策的贝叶斯型关联跟踪方法,此方法能够在信噪比低10~100倍的状况下获得与单扫描方法相当的性能,但同时会带来相当大的计算量。本文研究了面向航迹MHT中的关键算法,包括航迹得分计算与航迹树的生成、将航迹聚类和假设生成建模为图论问题并求解、N扫描回溯剪枝等,特别关注了这些算法过程的实现;提出了一种关联深度自适应(adaptive association depth, AAD)方法,使关联深度随关联场景的复杂程度自适应变化;仿真研究了本文提出的AAD-MHT跟踪密集目标的性能,结果和分析表明,与深度值固定为6的MHT相比,最大深度为6的AAD-MHT既能保证性能又有效降低了计算量。
多目标跟踪; 多假设跟踪; 数据关联; 关联深度自适应
0 引 言
多目标跟踪(multi-target tracking, MTT)技术在军事和民用领域应用非常广泛。在MTT中,航迹状态估计和数据关联常耦合在一起,前者基于后者给定的同源量测序列估计和预测目标状态,后者基于前者确定的状态预测及量测数据再根据某种准则判断量测的来源。就航迹状态估计而言,由于目标运动或观测模型的非线性,一般采用非线性滤波方法,如扩展卡尔曼滤波(extended Kalman filter, EKF)、无敏卡尔曼滤波(unscented Kalman filter, UKF)等;针对目标运动方式的不确定性,可以采用交互式多模型(interactive multiple model, IMM)方法以及变结构多模型(variable structure multiple model, VSMM)方法等。数据关联问题,由于量测的多种不确定性,相比滤波估计问题更加困难。量测的不确定性包括:①量测来源不确定,即传感器量测可能源于虚警、杂波、干扰或者目标、相邻目标等,同时目标也有可能未被检测到;②量测误差存在并且非线性。早期发展起来的数据关联方法适用于目标不密集环境下的单目标场景,包括最近邻(nearest neighbor, NN)方法以及概率数据关联(probabilistic data association, PDA)方法,将上述方法分别扩展到MTT中,即为全局最近邻(global NN, GNN)方法和联合概率数据关联(joint PDA, JPDA)方法。还有一些数据关联方法实际上是上述两种方法的改进,如最强邻(strongest NN, SNN)方法和Cheap JPDA等。GNN和JPDA是单扫描型方法,均基于上一次扫描已做出的关联决策和当前扫描的量测数据,来给出当前的关联决策。由于量测噪声、虚警杂波、目标机动的存在,在较困难的情景下仅利用单扫描的数据并不足以给出正确关联,因此需要联合多次扫描周期内的量测进行关联的多扫描型数据关联方法。
文献[1]中首次提出了一种完整的利用多扫描数据的数据关联方法。此方法在难以做出关联决策时维持各个可能关联情形作为关联假设,这些假设随着后续量测数据的接收不断生成子假设,即假设在扫描间传递,最后评估假设并做出决策。因此它是一种面向假设的多假设跟踪(hypothesisa-oriented multiple hypothesis tracking, HOMHT)方法[2]。
多假设跟踪(multiple hypothesis tracking, MHT)能够在信噪比低10~100倍的情况下获取与单扫描方法相当的性能[3]。Bar-Shalom 1989年在一篇关于MHT的综述文章中写道[4]:MHT在所有方法中考虑最全面,它能处理航迹起始、多目标及机动目标,它的劣势在于巨大的计算量和存储空间要求(高于PDA数个量级)、非常复杂的数据管理和巨量的输出航迹。因此在80年代,MHT的研究和应用进展缓慢。
在1990年到1993年间,文献[5-8]提出了面向航迹的MHT(track-oriented MHT,TOMHT)实现方案。在TOMHT中,不再维持全局假设集,而是维持假设航迹集,并由假设航迹集生成全局假设,利用全局假设概率计算航迹的概率,并据此删除低概率航迹以限制航迹数目。相比HOMHT,TOMHT方案的优势在于:①航迹综合输出容易,而在HOMHT中综合多个假设给出具有一致性的输出较为困难;②在表述同样多种关联可能时,维持假设航迹所需存储空间远较维持全局假设之所需低;③假设航迹生成简单,但全局假设的生成较为困难。针对TOMHT的最优全局假设生成问题,从1991年起,文献[9]将此问题建模为多维分配(multiple dimension assignment, MDA)问题,并利用递归拉格朗日松弛方法求解此问题[10],之后对此方法又做了改进[11],拉格朗日松弛方法的应用使得实时求解多传感器下多扫描、密集目标、密集杂波场景下的数据关联问题成为可能。文献[12]将假设航迹映射为图论中的顶点,将假设生成过程等价于求解最大加权独立集问题(maximum weighted independent set problem, MWISP),而MWISP是图论中的经典问题,在离散优化领域已被深入研究,因此结合已有的高效的MWISP求解算法,可以高效地生成全局假设。多种最优全局假设生成方法的研究成果、航迹分枝控制技术[13]以及计算能力的提高使TOMHT在国外获得广泛应用和深入研究。代表性的应用研究有:结合IMM的MHT以跟踪多机动目标[14];改进MHT并应用于群目标跟踪[15]、分离目标跟踪[16]、扩展目标跟踪[17]等特定场景;在视觉跟踪应用中将深度学习所得外观特征与MHT结合等[18]。
从2002年起国内有很多论文涉及到MHT的研究。代表性的研究及应用有机载雷达网系统的MHT框架设计和工程实现问题[19];分布式多传感器网络系统中IMM 结合MHT的算法[20];角度信息辅助的集中式多传感器MHT[21]以及基于因子图的地面密集目标MHT[22]等。
目前几乎普遍认为MHT是现代跟踪系统数据关联的首选方法[3],但是由于MHT算法的复杂度以及研究成本、研制周期、计算量的限制,国内在MHT领域起步较晚,且鲜有人对MHT在多传感器信息融合方面的应用进行研究和验证[20]。
本文着重研究了TOMHT算法在工程实现中的问题:给出了航迹得分计算方法及用途;结合跟踪门的使用阐述航迹树的生成;将航迹聚类和假设生成建模为图论问题,以便采用成熟高效的MWISP生成全局假设;提出了一种关联深度自适应(adaptive association depth, AAD)方法,使关联深度随关联场景的复杂程度自适应变化;仿真研究了本文提出的AAD-MHT跟踪密集目标的性能,仿真验证表明,本文所给出的算法具有良好的关联跟踪效果,同时又有效降低了计算量。
1 面向航迹的多假设跟踪算法
一个完整的TOMHT的逻辑框架如图1所示,由6个部分构成[23]:①对现有的航迹进行预测(即卡尔曼预测);②进行基于航迹得分的航迹删除和确认;③对在航迹删除后幸存的航迹进行分簇;④在每个簇中独立地进行全局假设的生成、航迹全局概率的计算;⑤基于最优全局假设的N扫描回溯剪枝及基于全局概率的航迹删除;⑥用当前时刻量测对幸存航迹进行更新,即卡尔曼滤波,同时综合剩余假设航迹向用户提供输出。研究表明上述6个阶段主要涉及航迹得分、航迹树的生成、航迹聚类、全局假设生成、N扫描回溯剪枝等5项关键算法,下面在理论和应用结合层面上对这些关键算法进行论述。

图1 TOMHT的逻辑框架Fig.1 Logic overview of TOMHT
1.1航迹树的生成
TOMHT一般会引入航迹树结构。一株航迹树对应一个目标,树上每一条从根到叶的路径构成该目标的一组量测历史记录,其中至多只有一条路径反映了真实目标的航迹。图2可说明航迹树形成过程:在k-1扫描,将航迹量测预测值附近区域设为相关门,只有位于相关门内的量测(如图2中的zk-1,1和zk-1,2)才可与航迹关联,由于目标可能不被探测到,这时航迹可不关联任何量测,即关联zk-1,0(空量测,以深色节点表示)。接着根据关联结果获得各个航迹分支在k扫描的量测预测,并可设置相应的相关门,再根据相关门内的量测,将航迹树伸展到k扫描。
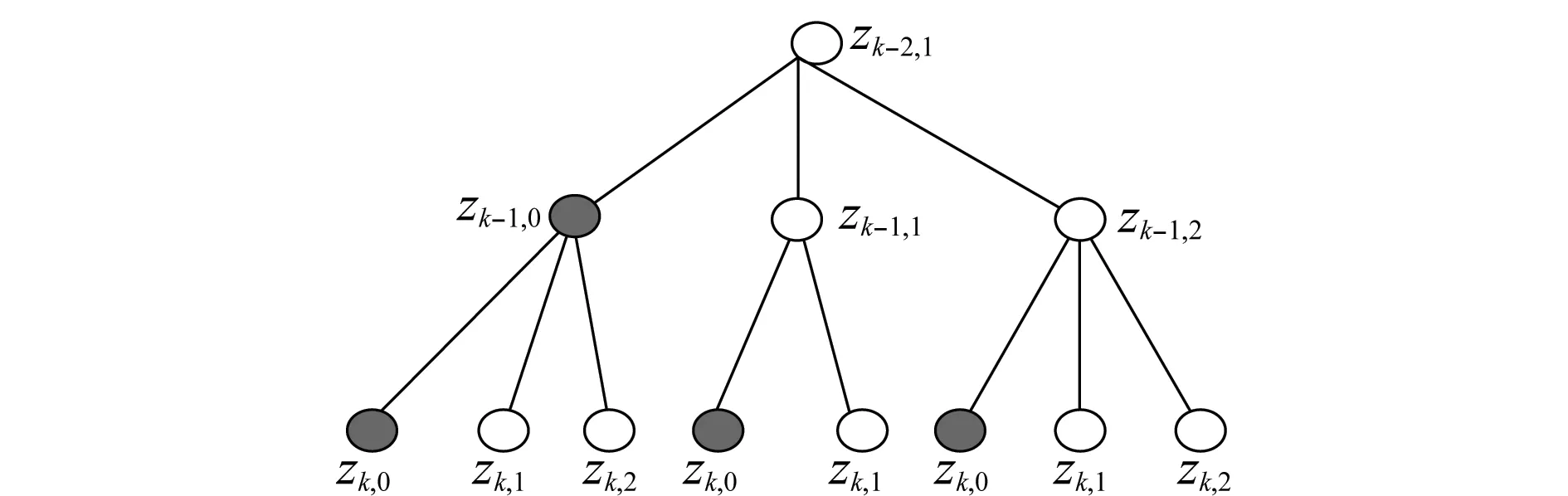
图2 航迹树的形成Fig.2 Tree structure formation in TOMHT
显然,随着时间的推移,航迹树的数量会越来越多,树的结点数也会急剧增大。除了采用相关门技术控制假设航迹数目,还需要根据航迹得分对航迹进行剪枝操作,以及根据假设航迹的后验概率进行N-扫描回溯剪枝和全局剪枝。
1.2航迹得分
在MHT中必须对假设进行评估,其评估准则是假设后验概率。分析假设后验概率的计算式,可将此概率的对数值分解到可递推计算的航迹概率似然值(即航迹得分)。记P{Θk,s|Z1∶k}为1到k扫描所有量测Z1∶k条件下假设Θk,s(k扫描第s个全局假设)的概率,设Θk,s在k+1扫描的某个子假设为Θk+1,l,则假设后验概率[24]的对数形式为
(1)
式中,ci为第i扫描中不随假设变化的常数;δt指示Θk,s中航迹Tt是否关联k+1时刻的量测;v为k+1扫描新出现目标的数目;λfa和λnew分别表示虚警杂波密度和新杂波密度;PDt(k+1)表示航迹Tt所代表目标在k+1扫描被传感器观测到且其量测落入相关门的概率;ft[zk+1,jt]表示在量测取为zk+1,jt(即航迹Tt关联量测zk+1,jt)时的概率密度函数值(pdf),在利用卡尔曼滤波预测下一扫描量测时此pdf是容易计算的。
式(1)等式左侧设为Θk+1,l的假设得分,分析可知:假设得分可递推计算,假设得分增量可分解到每条航迹上;新目标对假设得分的贡献为ln(λnew/λfa);航迹Tt不关联任何量测时贡献为ln(1-PDt);航迹Tt关联量测zk+1,jt时的贡献为ln[PDtft[zk+1,jt]/λfa]。分解得分增量实际上是将假设得分分解到每条航迹上,即每条航迹都有得分。航迹Tt在k扫描的得分sk可定义为
(2)
根据航迹得分的定义,假设得分为构成假设的所有航迹的航迹得分之和,从而可用于计算航迹后验概率。航迹得分[25]还可用于确定航迹的状态,一般根据航迹得分将航迹分为起始航迹(单点航迹)、暂时航迹(得分较低的多点航迹)、确认航迹(得分超过某门限的多点航迹)、删除航迹(航迹得分过低或与历史最高得分之差超过一定门限)。
1.3航迹聚类
由于某些目标在时空中的可区分性很高,因此可将所有的假设航迹划分成子集,在每个子集中独立地进行假设生成、全局级航迹删减和航迹更新等操作,以免因假设组合导致复杂度过大。假设航迹子集即为航迹类或航迹簇(若干共享量测的航迹树组成的集合)。
MTT算法一般假设:任何量测最多源于单个目标;任何目标在单个扫描中最多产生一个量测。因此,不同航迹类中的假设航迹必定不能共享量测。将假设航迹映射为图论中图的顶点,航迹共享量测则对应顶点是相邻的(即顶点间存在边)。聚类即为顶点集的划分操作,根据聚类原则,相邻顶点必在同一集合中,根据此性质,聚类对应将所有顶点划分为若干个极大连通子集的操作,此过程可由深度优先搜索算法实现。
由于航迹间是否共享量测在航迹聚类和全局假设生成中都是必需的,故在实现时需要维持航迹相容性矩阵M:若航迹i与航迹j共享量测,则Mij=1,否则Mij=0(相容即不共享量测)。可通过2个步骤确定M:①如果两航迹在前一个扫描(即父航迹)是不相容的,则这两个航迹也是不相容的;②如果在当前扫描两航迹关联同一个量测,则这两个航迹也是不相容的。
1.4全局假设生成
航迹得分只能反映航迹本身的量测历史与运动模型、观测模型的符合程度,它没有考虑其他航迹、量测对航迹的影响。在MTT中必须通过假定了全部量测来源的全局假设来进行整体的数据关联。全局假设是互不共享量测的假设航迹集合,不在任何假设航迹中出现的量测认为是虚假量测,因此它实质上假定了所有量测的来源。全局假设可在每一个簇中独立地形成,故假设生成很容易并行处理。由于航迹树内航迹共享一个根结点,所以一株航迹树内的所有航迹是互不相容的,因此一个全局假设中至多包含某个航迹树中的一条航迹。
当前扫描下的最优假设(得分最高的假设)给出了在目前数据下具有最大概率的数据关联结果,它可用于关联决策。如果生成所有较优假设并使未生成假设的概率和很小,则能够较准确计算假设航迹的后验概率。因此应尽可能生成所有的较优假设[23]。具体来说,如果最优假设的得分为smax,设其概率为Pmax,则应该生成得分在smax-Δsthr的假设,相应的假设概率为e-ΔsthrPmax,一般设Δsthr=10。
考虑到MWISP与基于MDA的MHT实现比较起来更加简明,且可以利用图论中成熟的算法,因而本文采用MWISP获得全局假设。图3给出了将假设航迹映射到图的例子,左边的航迹树表示到k次扫描时的4个航迹,树的每个节点中的数字为航迹在对应扫描中所关联量测的标号,因此航迹T1、T2、T3互不相容(共享根节点量测),T2和T4在k次扫描时共享量测2,故不相容,假定每个航迹的得分为其航迹标号数值,故可得右边的航迹图,图的顶点数字对应假设航迹的得分。显然加权独立集按照航迹得分加权和从大到小排序有{T3,T4},{T1,T4},{T4},{T3},{T2}和{T1},即这4个航迹可生成6个全局假设,其中最优全局假设为{T3,T4}。

图3 假设航迹到图的映射Fig.3 Mapping from hypothesis tracks to track graph
通过求解MWISP获得较优假设是TOMHT算法的关键步骤,因为MWISP是图论中的NP问题,在问题规模较大时,主要指目标密集或虚警很高情况下,假设生成是TOMHT算法计算量的主要来源。一种启发式方法贪心随机自适应搜索方法(greedyrandomizedadaptivesearchingprocedure,GRASP)可用于求解此问题[26]。
TOMHT的假设生成和一般的MWISP不同之处是MWISP中所有顶点的权值必定均为非负数,而TOMHT假设生成中允许部分航迹得分为负值,只要假设得分满足条件即可。因此假设生成过程可分为以下3步:
步骤 1考虑所有的正得分航迹,利用MWISP算法获得大量较优全局假设;
步骤 2从负得分航迹集构成的图中生成大量独立集,保证独立集的权值和不超过Δsthr(这种独立集中元素个数一般不大,在10以下),并将独立集按权值和降序排列;
步骤 3进行合并,若最大假设得分为smax,对步骤1所获得分为si的较优假设选取步骤2中的权值和在smax-si-Δsthr以上的独立集进行合并,如果合并后还是独立集,则将合并后的独立集作为一个较优全局假设(步骤1所有较优假设都在最后的较优全局假设集内)。
1.5N扫描回溯剪枝和全局级航迹删减
N扫描回溯剪枝,利用了k-N+1,…,k-1,k这N次扫描的数据确定第k-N+1次扫描数据的关联决策。图4表示N=3时的N扫描回溯剪枝,涂灰的节点表示对应航迹出现在最优假设中(称为最优节点),当前扫描为第k次扫描,对于tree1,从最优节点开始,按树的分支路径往前回溯,回溯到k-2次扫描,在k-2次扫描中有根节点,但又不是最优假设中航迹的根节点的所有假设航迹分支都被删除。由于tree2在k-2次扫描不存在关联不确定性,因此不做3-扫描回溯剪枝;tree3必定没有航迹出现在最优假设中,因为它与tree1最优节点对应航迹共享量测,由于k-2的量测来源已确定,因此tree3被删除。
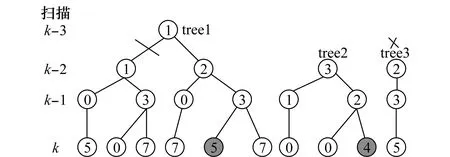
图4 3-扫描回溯剪枝Fig.4 3-scan pruning
全局级航迹删减是对N扫描回溯剪枝幸存的假设航迹,再依据假设航迹的后验概率式(3)进行删除。
(3)
式中,Hi(i=1,2,…,NH)为全局假设,其对应得分为si。全局级航迹删减过程分两个步骤进行:①根据概率门限法,删除后验概率低于门限的假设航迹;②对每个航迹树,删除若干个低后验概率的航迹,以保证每个航迹树内假设航迹数不超过定值。
由上述可见全局假设在N扫描回溯剪枝和全局级航迹删减中起非常重要的作用。
本节对TOMHT过程所涉及的关键算法进行了详细描述:航迹得分是航迹生命期管理和对数据关联假设进行评估的基础;航迹树是一种有效的航迹组织结构,据此可方便地做回溯剪枝以给出具有一致性的关联决策;聚类即为求解极大连通子图问题;假设形成归结为获得较优加权独立集问题;全局级航迹删除则依赖航迹后验概率。
TOMHT算法实用性取决于能否有效控制假设航迹数目以减少计算量,一般有基于航迹本身的航迹级删减、扫描回溯剪枝、全局级航迹删减和航迹合并技术。
2 关联深度自适应方法
MHT方法利用若干个扫描的后继量测解决当前扫描的关联不确定性,随着后继扫描数目的增加所需要保留的假设航迹数目呈指数增加,所以后继扫描数目N不宜过大,但N值过小可能导致所利用的后续量测信息不足以解决当前关联不确定性。目前很多跟踪系统中关联深度N一般是事先设定的,文献[3]给出了经验性建议N≥5。当关联深度N=1时,MHT算法退化为具有航迹起始与终结等功能的GNN算法。
实际上,关联深度N应该依赖于跟踪场景:对目标和杂波密集的困难情景,需要更多量测信息来共同做出关联决策,N值应较大;在目标的时空区分性好、杂波和干扰少的简单情景,N值应较小,甚至N=1,即GNN方法足以给出正确关联决策。在同一监视空间,有些区域的目标需要较大的关联深度,某些区域所需关联深度很小。对同一个目标,某段时间需要的关联深度较大,另一段时间所需深度可能很小。因此,事先设定统一关联深度,对简单情景增加了不必要的计算量而不能改善关联结果,甚至延迟了关联决策;对极为复杂情景的目标,预先设定的关联深度可能还不够。因此,设定关联深度,使其与跟踪场景相适应,有利于高效利用计算资源和提高复杂场景下算法性能。
下面描述TOMHT框架下AAD方法,此方法依赖于最优假设和航迹后验概率,对每个航迹树设定自适应变化的关联深度,并且该变化过程分两步进行,即关联深度扩大和缩减。关联深度扩大用于替代扫描回溯剪枝过程,而关联深度减小则在全局级航迹删减后的航迹更新与合并步骤中执行。
关联深度扩大过程可描述如下:
步骤 1将航迹树按树中分支航迹的最大得分作降序排列,排序后的航迹树为Tri(i=1:NTree),树中分支航迹的最大得分有s1≥s2≥…≥sNTree。设最小深度Nmin=1,设最大深度Nmax=8。令i=1,s=1,转入步骤2。
步骤 2当Tri中某假设航迹Tij隶属于最优假设,则转入步骤3,否则转入步骤7。
步骤 3设Tri对应的关联深度为di,当di=Nmax则执行步骤4后转入步骤6,否则di 步骤 4在Tri中对Tij从当前的第k扫描回溯到k-di+1扫描,将Tri中在k-di+1扫描异于Tij的所有航迹分支删除,同时将其他航迹树中在k-di+1扫描与Tij共享量测的所有航迹删除。 步骤 5设pij为Tij的后验概率,Tri中在k-di+1扫描与Tij关联相同量测的所有航迹(包括Tij)的后验概率之和为pi,如果pij≥ps_thr且pi≥pb_thr,则执行步骤4,再转步骤6,否则认为di扫描量测不足以支持决策,故di:=di+1,转入步骤6。 步骤 6令i:=i+1,如果i≤NTree,转入步骤2,否则s:=s-1,令l=1并转入步骤8。 步骤 7令is=i,然后s:=s+1,转入步骤6。 步骤 8如果s 步骤 9设航迹树Tril在k-dil+1扫描中以j量测为根的航迹分支的后验概率之和为pj,其中后验概率和最大的量测为jl。若dil=Nmax则执行步骤10后转入步骤12,否则dil 步骤 10保留jl量测为根的航迹分支而删除其他分支,删除其他航迹树Trij(1≤j≠l≤s)中关联jl量测的航迹。 步骤 11如果pjl≥pb_thr,执行步骤10后转入步骤12,否则dil:=dil+1,转入步骤12。 步骤 12令l:=l+1,转入步骤8。 关联深度缩减过程:对于航迹树Tri,其关联深度为di,如果航迹树中所有航迹从k-di+1到k-di+ni次扫描的量测历史序列一致,则取di:=max(di-ni+1,Nmin)。 图5示例说明关联深度自适应过程,其中粗线表示此航迹分支在最优假设中。设计两个关联决策参数Pb-thr=0.4和Pb-thr=0.8分别为单航迹显著概率和分支显著概率。在Tree1中,当前深度为3,由于最优假设所含航迹所在子树所有航迹后验概率之和为0.7,小于Pb-thr,因此认为3个扫描的数据不足以给出可信的关联决策;在Tree2中,最优假设所含航迹的后验概率0.4不低于Ps-thr,此航迹所在子树所有航迹分支的后验概率和为0.85,高于Pb-thr,因此可进行3-扫描回溯剪枝,在关联深度扩大阶段保持深度为3,到了关联深度缩减阶段,关联深度减小为2;Tree3的关联深度为2,不满足关联决策条件,关联深度扩大为3。 图5 关联深度自适应过程示例Fig.5 Example of an AAD process 本节给出两个仿真实验,以说明本文关AAD-MHT方法的有效性。 3.1几乎交叉目标跟踪实验 两个目标具有相同速度,先相互靠近,再逐渐远离,目标间最近距离为150m, 扫描周期T=2s,设目标最大速度Vmax=300m/s,检测概率PD=0.75,虚警杂波密度λfa=10-9m-2,新目标密度为λnew=10-10m-2。在x,y方向上的量测噪声均方差为100m。实验结果如表1和图6所示。 表1 算法结果对比 表1给出N=1、N=6和AAD下的多个性能指标比较,NT为真实航迹(指至少有一半量测源于真实目标的航迹)数目;RMC为误关联率; RCC为真实航迹正确关联率;OSPA为最优子模式分配(optimalsub-patternassignment)[27]距离,用于度量关联结果与真实航迹之间的差异性。由表1和图6(b)可见,N=1时发生了航迹交叉和航迹多次起批;表1和图6(c)均说明,AAD获得了与N=6相同的结果,均与真实航迹一致,但是其运行时间仅为固定N的48%。 图7给出了两个航迹对应航迹树的关联深度随扫描的变化情况。前20次扫描中,目标间距较大,此时关联深度N=1;第20个扫描后,目标间距减小,单扫描量测不足以支持关联决策,故N值逐渐增大,直到Nmax;第40个扫描后两目标逐渐远离,故N值逐渐减小直到Nmin。 图6 几乎交叉目标跟踪实验结果Fig.6 Results of tracking nearly crossed targets 图7 关联深度N的自适应变化Fig.7 Adaptive change of association depth N 3.2编队飞机跟踪实验 本实验将AAD-MHT算法用于跟踪编队飞机目标。飞机的相对位置定义为(a,b,c),分别表示某飞机在领头机的后方a处、右边b处、上方c处。共有4架飞机编队飞行,除领头机外,其余3架的相对位置为(2,-0.8,0.1)、(4.5,0.8,0.2)和(6.5,1.6,0.2)(单位为km)。雷达观测坐标系为极坐标系,距离误差标准差为200m,方位角和俯仰角误差标准差均为0.2°。λfa=10-2m-1·rad-2,λnew=10-6m-1·rad-2,扫描间隔为4s,检测概率为0.3,假定目标运动符合常加速度模型,目标最大速度为1 000m/s。 图8给出了编队飞机跟踪结果的平面显示,由图可见,航迹均开始于第(9)区域,结束于第(1)区域。由图8(a)可以看出,GNN所输出航迹多次交换、航迹起始较晚且其中有些航迹在后期发生了严重的关联错误,而图8(b)说明,AAD-MHT几乎没有航迹互换且所有航迹均较快地起始。 图8 编队飞机目标跟踪结果Fig.8 Results of tracking target in formation 表2给出了几项指标比较,说明在平均意义下,AAD-MHT的起始时刻比GNN早28.5个扫描,并且航迹持续时间较长,真实航迹正确关联率高于后者。 两个仿真实验结果表明,AAD方法确实能够根据关联情景的难易程度自适应地调整N值,能够在兼顾性能的同时减小计算量,说明了AAD-MHT算法的有效性。 表2 不同算法性能比较 MHT的基本思想是对每种关联情况多扫描考察,而非根据现有数据立即给出不可逆转的关联决策。由于关联情况的多样性,MHT算法的计算量必然很大,这给工程上实时应用提出了挑战。考虑到很多假设是极低可能的假设,因此必须对MHT算法的各个步骤做精心设计,尽可能保留高可能假设,同时尽可能降低假设航迹数目。本文重点描述了TOMHT的关键算法及具体实现,包括航迹树生成、航迹得分计算、航迹聚类、假设生成、航迹删除等。基于关联深度应与跟踪场景相匹配的思想,提出了一种利用航迹后验概率的AAD方法,每个航迹树的关联深度可随着关联情况自适应的变化。此方法在复杂情况下使用较大的关联深度保证了跟踪性能,在简单情况下使用较小的关联深度降低了计算量。本文的两个仿真实验验证了本文基于AAD-MHT的有效性。 [1]ReidDB.Analgorithmfortrackingmultipletargets[J].IEEE Trans. on Automatic Control, 1979, 24(6):843-854. [2]AntunesDM,MatosD,GasparJ.Alibraryforimplementingthemultiplehypothesistrackingalgorithm[EB/OL].[2015-11-03].http:∥arxiv.org/abs/1106.2263. [3]BlackmanSS.Multiplehypothesistrackingformultipletargettracking[J].IEEE Aerospace and Electronic Systems Magazine, 2004, 19(1):5-18. [4]Bar-ShalomY.Recursivetrackingalgorithms:fromtheKalmanfiltertointelligenttrackersforclutteredenvironment[C]∥Proc.of the IEEE International Conference on Control and Applications, 1989:675-680. [5]KurienT. Issues in the design of practical multitarget tracking algorithms[M]∥Bar-ShalomYed. Multitarget-multisensor tarcking: advanced and applications.Norwood:ArtechHouse, 1990. [6]DemosGC,RibasRA,BroidaTJ,etal.ApplicationsofMHTtodimmovingtargets[C]∥Proc.of the Signal and Data Processing of Small Targets, 1990:287-309. [7]WerthmannJR.Step-by-stepdescriptionofacomputationallyefficientversionofmultiplehypothesistracking[C]∥Proc.of the Signal and Data Processing of Small Targets, 1992:288-300. [8]ChanDS,HarrisonDD,LanganDA.Trackinginahighclutterenvironment:simulationresultscharacterizingaBi-levelMHTalgorithm[C]∥Proc.of the Signal and Data Processing of Small Targets, 1993:540-551. [9]PooreAB,RijavecN.Multi-targettrackingandmulti-dimensionalassignmentproblems[C]∥Proc.of the Signal and Data Processing of Small Targets, 1991:345-356. [10]RogerDW.Parametricandcombinatorialproblemsinconstrainedoptimization,ADA264229[R].California:CaliforniaUniversifyDavisDepartmentofMathematics, 1993:1-25. [11]PooreAB,RobertsonAJIII.Anewlagrangianrelaxationbasedalgorithmforaclassofmultidimensionalassignmentproblems[J].Computational Optimization and Applications, 1997,8(2): 129-150. [12]PapageorgiouDJ,SalpukasMR.Themaximumweightindependentsetproblemfordataassociationinmultiplehypothesistracking[C]∥Proc.of the 8th International Conference on Cooperative Control and Optimization, 2009: 235-255. [13]WilliamsJL.Gaussianmixturereductionfortrackingmultiplemaneuveringtargetsinclutter,ADA415317[D].Ohio:AirForceInstituteofTechnology, 2003. [14]BlackmanSS,DempsterRJ,RoszkowskiSH.IMM/MHTapplicationstoradarandIRmultitargettracking[C]∥Proc.of the Signal and Data Processing of Small Targets, 1997: 429-439. [15]CoraluppiS,CarthelC.Aggregatesurveillance:acardinalitytrackingapproach[C]∥Proc.of the 14th International Conference on Information Fusion, 2001:1-6. [16]ObataY,MaekawaR,ItoM,etalTrackingalgorithminheritingsmoothingvectorinsplittingtargettracking[C]∥Porc. of the ICROS-SICE International Joint Conference, 2009: 3020-3025. [17]ZhaiG,MengHD,ZhongZW,etal.Amultiplehypothesistrackingmethodforextendedtargettarcking[C]∥Porc. of the International Conference on Electrical and Control Engineering, 2010: 109-112. [18]KimC,LiFX,CiptadiA,etal.Multiplehypothesistrackingrevisited[EB/OL].[2015-12-10].http:∥web.engr.oregonstate.edu/~lif/MHT_ICCV15.pdf. [19]WangZ.Airbornemulti-sensordatafusiontechnology[D].Nanjing:NanjingUniversityofScienceandTechnology,2010. (王智.机载多传感器数据融合技术研究[D].南京:南京理工大学,2010.) [20]LuYB,SunW.Amulti-sensordatafusionalgorithmbasedMHT[J].Journal of China Academy of Electronics and Information Technology,2008,3(1):24-28. (陆耀宾,孙伟. 基于MHT的多传感器数据融合算法[J].中国电子科学研究院学报, 2008, 3(1): 24-28.) [21]WangH,SunJP,FuJT,etal.Angle-aidedcentralizedmulti-sensormultiplehypothesistrackingmethod[J].Journal of Electronics & Information Technology,2015,37(1):56-62. (王欢,孙进平,付锦斌,等.角度信息辅助的集中式多传感器多假设跟踪算法[J].电子与信息学报, 2015, 37(1):56-62.)[22]WangH,SunJP,LuST.Factorgraphaidedmultiplehypothesistracking[J].Science China Iinformation Science, 2013, 56(10):1-6.[23]BlackmanSS,PopoliRF. Design and analysis of modern tracking systems[M].Boston:ArtechHouse, 1999:1069-1075. [24]Bar-ShalomY,LiXR. Multitarget-multisensor tracking: principles and techniques[M].StorrsCT:YBSPublishing, 1995: 337-338. [25]Bar-ShalomY,BlackmanSS,FitzgeraldRJ.Dimensionlessscorefunctionformultiplehypothesistracking[J].IEEE Trans. on Aerospace and Electronic Systems, 2007,43(1):392-400. [26]RenXY,HuangZP,SunSY,etal.AnefficientMHTimplementationusingGRASP[J].IEEE Trans. on Aerospace and Electronic Systems, 2014, 50(1):86-100. [27]Ba-NguV,Ba-TuongV,SchuhmacherD.Aconsistentmetricforperformanceevaluationofmulti-objectfilters[J].IEEE Trans. on Signal Processing, 2008, 56(8):3447-3467. Multiple hypothesis tracking with adaptive association depth CHEN Hang, ZHANG Bo-yan, CHEN Ying (BeijingInstituteofRadioMeasurement,Beijing100854,China) Multiple hypothesis tracking(MHT) is a Bayesian association method that evaluates association hypotheses among multiple scans and makes evaluation-based decisions. Comparing with the single hypothesis method, MHT can work reasonably under 10~100 times lower signal-noise ratio (SNR) but it needs much more computational load. The implementation of track-oriented MHT (TOMHT) is studied and some key points are investigated, include calculating the track score, generating the track tree, modeling track clustering, hypotheses generating as problems in graph theory andN-scan pruning, etc. In the TOMHT framework, an adaptive association depth (AAD) method is proposed. This method makes the association depth change adaptively with the complexity of scenarios. Its performance is investigated by several simulation experiments on tracking closely targets. The results and analysis show that the performance of AAD-MHT is nearly the same as MHT but the computational load is much lower. multi-target tracking(MTT); multiple hypothesis tracking(MHT); data association; adaptive association depth(AAD) 2015-12-24; 2016-06-08;网络优先出版日期:2016-07-03。 TN 953 A 10.3969/j.issn.1001-506X.2016.09.06 陈杭(1990-),男,硕士研究生,主要研究方向为雷达信号处理与数据处理。 E-mail:chenhanghb@126.com 张伯彦(1957-),女,研究员,博士,主要研究方向为现代雷达控制与数据处理、机动多目标跟踪、数据融合。 E-mail:zhbyhktk@163.com 陈映(1984-),女,高级工程师,博士,主要研究方向为雷达数据处理、弹道目标跟踪。 E-mail:michelle_cv@163.com 网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20160703.1240.004.html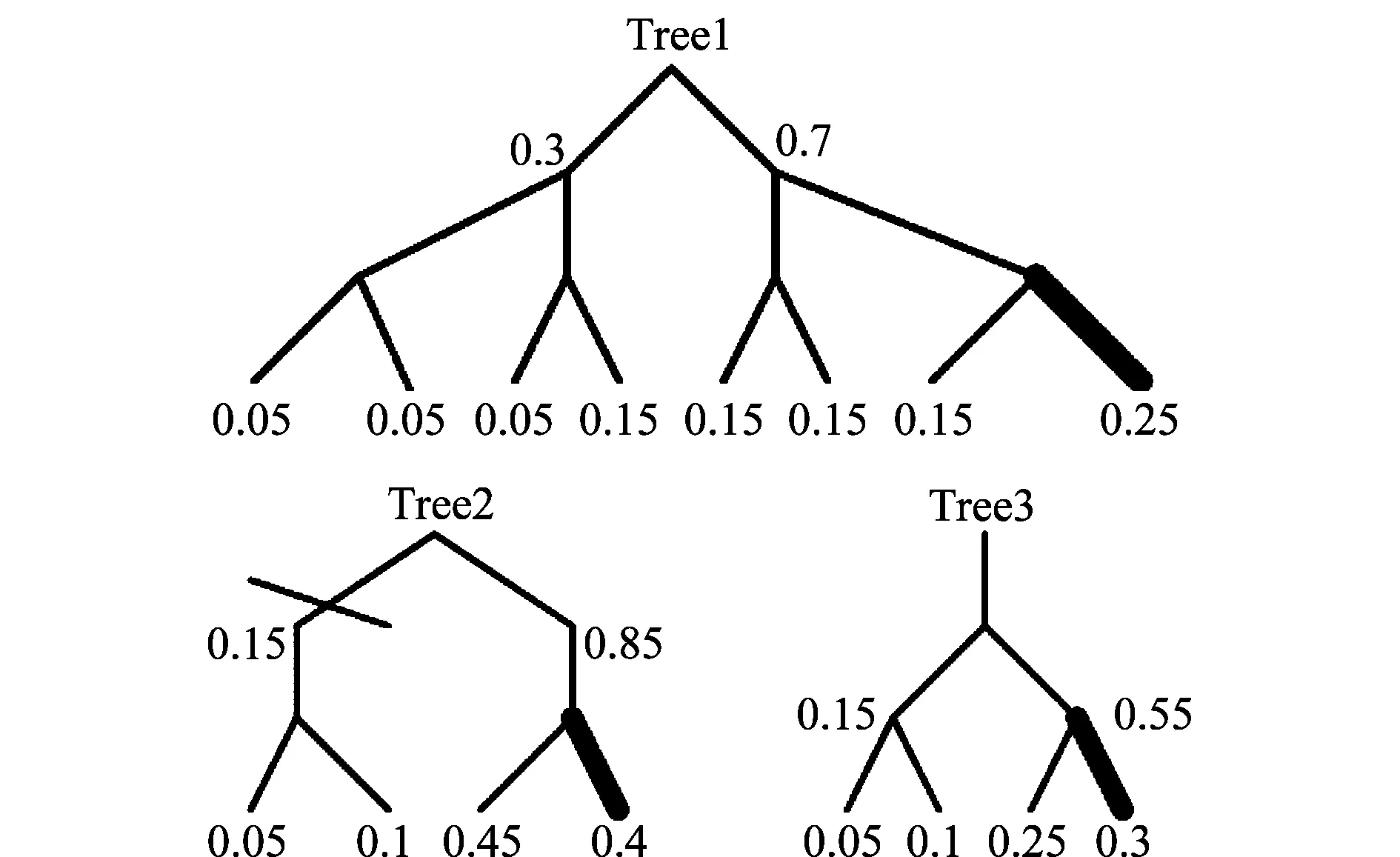
3 仿真实验与分析

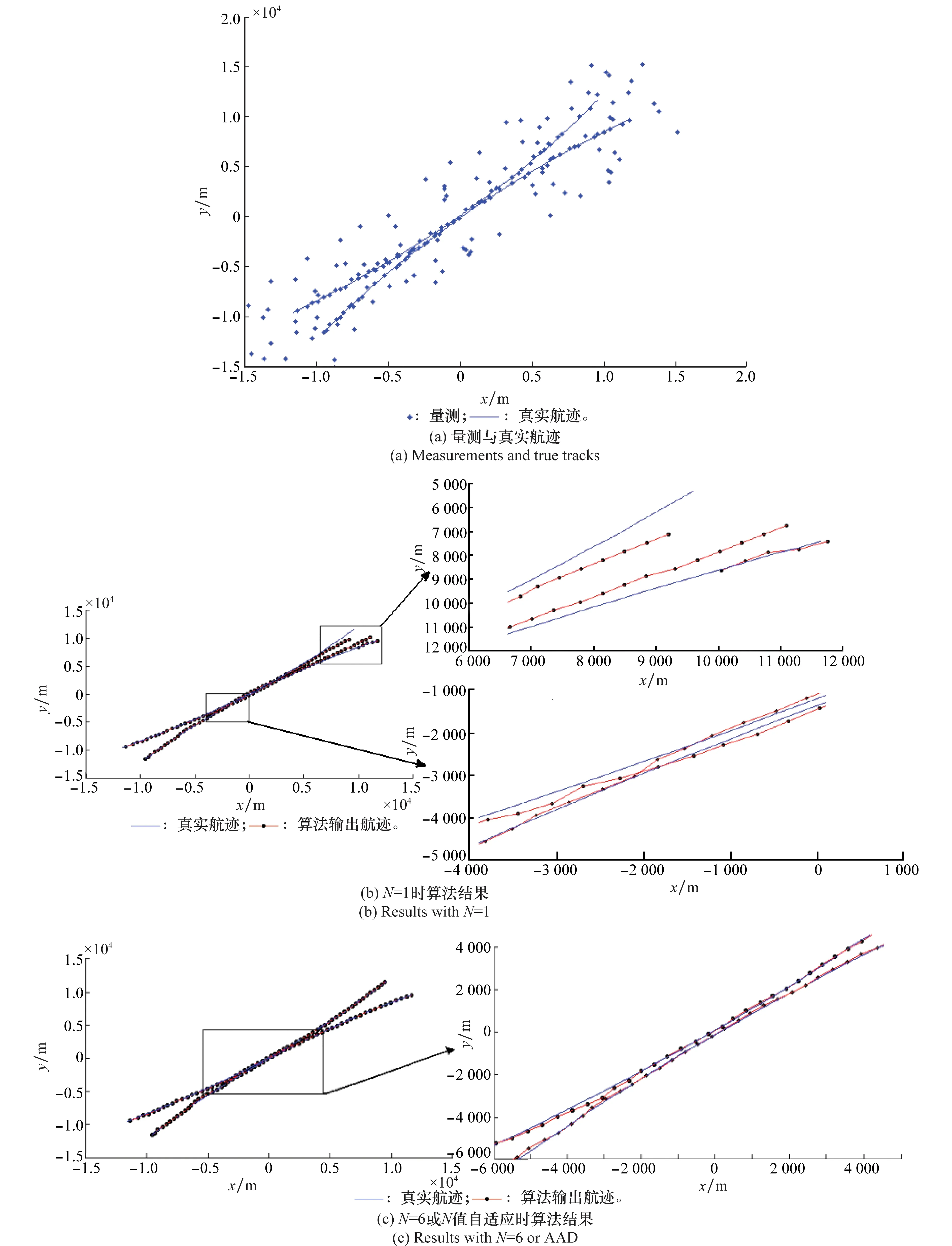



4 结 论

