滑窗式无偏多平台无源定位算法

关　欣, 关　欣, 陶　李, 衣　晓

(1. 海军航空工程学院电子信息工程系, 山东 烟台 264001; 2. 海军航空工程学院航空训练基地, 山东 青岛 266108)



滑窗式无偏多平台无源定位算法

关欣1, 关欣1, 陶李2, 衣晓1

(1. 海军航空工程学院电子信息工程系, 山东 烟台 264001; 2. 海军航空工程学院航空训练基地, 山东 青岛 266108)

针对纯方位系统单机动平台在不具有比机动目标更高一级的机动运动时,无法满足系统可观测性的问题,提出了一种适用于多平台的无源定位算法。该算法根据目标与平台之间的几何关系得到一个包含目标初始位置和分量速度的伪线性方程组。为减少求解方程组的计算量,保证定位的实时性,对常规的最小二乘法进行了加滑窗处理。通过对观测向量和系数矩阵的分析,证明了算法对目标状态的估计具有无偏性。仿真实验验证了算法的有效性,并讨论分析了平台运动的速度和方向等因素对算法定位性能的影响,得到了保证算法定位性能的平台与目标相对运动关系。

源定位; 纯方位系统; 最小二乘法; 多机动平台; 滑窗式

0　引　言

无源定位技术凭借其隐蔽性强、探测距离远等优点在战场上占据了重要地位。其中,仅依靠方位角信息进行测量的测向定位技术更是以其计算快、设备简单的优势成为无源定位技术研究的重点[1-3]。尽管被动雷达检测到的目标信息中,方位角信息的可信度最高[4],但由于该技术无法直接获得目标的距离信息,故其为一个不完全可观测系统。对于单站系统来说,由于每观测一次,除了自身的运动参数和位置信息外,只能得到一个方位角信息,信息量的不足使得平台只有在具有比机动目标更高一级的运动时,才可以对目标定位[5-6]。而多观测平台对目标定位时,一次观测中每个平台均可以获得一个方位角,通过不同方位线的交叉便可以确定目标位置,避免了单平台定位可观测性的局限性,成为无源定位的一个重要研究方向[7-8]。

测向定位本质上属于非线性估计问题。其基本思路是将方位角信息和待测目标的未知参数转换为伪线性方程组。由于系统是高度非线性的,并且初始条件的精度很难得到保证,故扩展卡尔曼滤波(extended Kalman filter, EKF)[9]算法很容易出现发散的情况。最小二乘误差算法(least-squared error, LSE)[10-11]没有消除伪线性方程组中的系数矩阵的误差,导致其最后的估计是有偏的。虽然通过奇异值分解的方法,总体最小二乘估计(total least-squared, TLS)算法[12-16]解决了LS算法有偏估计的问题,但代价是运算量大、实时性差。

本文在LS算法的基础上,提出了一种适用于多站测向定位的滑窗式最小二乘定位(sliding window least-squares, SWLS)算法。其基本思路为获得目标与平台相对关系的伪线性方程组,其解即为要求解的目标运动参数。与LS算法不同的是,SWLS算法通过滑窗方式获取系数矩阵和观测向量,并以递推方式进行求解计算[17]。该算法在保证定位精度的同时,大幅减少了计算量,提高了定位速度。

1　定位原理

图1所示为二维空间中平台个数为2时,目标与平台之间的相对关系。

图1　平台与目标之间的相对关系Fig.1　Relative relationship between platforms and target

多平台情况与之类似,以多机动平台为模型进行推导。显然,可以得到

(1)式中,dik表示k时刻第i个平台与目标T的相对距离；vik为其对应的单位矢量。

令k时刻的平台位置为(xik,yik),其与目标的方位角为βik(i≥2),目标位置为(xTk,yTk),则有

(2)令目标作匀速直线运动,x方向和y方向的速度分别为vx和vy,初始位置为(xT0,yT0),k时刻目标位置为

(3)将式(3)代入到式(2)中,并将矩阵形式改写成方程组,有

(4)整理式(4)并消去dik,可得

(5)将k时刻的累积测量记成矩阵形式Zk=HkXk

(6)式中,观测向量Zk和系数矩阵Hk分别为

(7)

(8)状态变量Xk为

(9)

2　算法模型

一般情况下采样次数k>2,故观测向量Zk是超正定矩阵,只能求解Hk的广义逆矩阵。式(6)的最小二乘解为

SWLS算法通过滑窗方式使观测向量Zk和系数矩阵Hk得到动态序贯更新,使它们的维数不随观测次数的增多而变大。这样既不以定位精度的下降为代价,又保证了计算量的减少。

将滑窗部分的观测向量和系数矩阵分别记为

(11)

(12)

记

(13)

则有

(14)

利用矩阵反演公式可得

(15)

式中,Ii表示i阶单位矩阵,这样Pk可由Pk-t递推得到,由式(10)可知

(16)

将式(14)代入式(16),并化简可得

(17)

这样,Xk可由Xk-t递推得到。

为考察本文算法的复杂度,同样忽略式(17)中Pk的矩阵逆运算,此时SWLS算法的复杂度为O(t4)。而滑窗长度t为一常数,可根据实际情况对定位精度和定位时间的要求进行选择。

若滑窗长度为t,起始点为l,算法具体流程如图2所示。

图2　滑窗式最小二乘定位算法流程图Fig.2　Algorithm process diagram of sliding window least-square localization algorithm

可以看出l=k和t=1时,分别存在两种极限情况,此时算法分别演变为LS算法和递推式LS算法。

3　无偏性验证

定理 1多站测向定位系统中,测量噪声为独立不相关的高斯白噪声时,对目标初始位置和分量速度的估计是无偏的。

证明假定方位角在测量过程中含有微小误差δβ,且δβ～(0,σ2),各平台测量误差独立不相关。记方位角测量值β′=β+δβ,于是有

(18)

(19)

通过对式(7)求导可得

(20)

利用δβ≈∂β和δ(Zk)≈∂(Zk),有

(21)

同样对式(8)求导可得

(22)

利用δβ≈∂β和δ(Hk)≈∂(Hk),同样有

(23)

将式(17)、式(18)代入式(6)可得

(24)

式中,δx为定位算法的偏差。将式(24)展开,并忽略具有两个微元因子的乘积项,可以得到

(25)

将式(20)、式(22)代入式(25),并结合式(3)整理可得δXk=0。

δx的协方差矩阵为

(26)

其中

(27)

dik为k时刻平台i与目标之间的距离。

证毕

4　算法仿真

仿真环境:目标作匀速直线运动,运动速度为200m/s,运动方向与X轴正方向夹角为45°,起始点为(0,0)。平台1和平台2均以150m/s的速度作匀速直线运动,运动方向与X轴正方向夹角分别为50°和40°,起始点分别为(30 000,0)、(0,30 000)。方位角测量误差服从零均值正态分布,测量周期为1s,连续观测200点。进行100次蒙特卡罗实验,算法定位精度以圆概率误差(circularerrorprobability,CEP)作为度量,表示为

当筛选完音乐课程资源之后，教师就可以把音乐资料通过文本形式或制作成DVD、VCD储存到资源库中。而且，也可以将制作好的CD、音乐文本上传，方便有需要的教师在局域网上查阅相关资料。在使用之后，教师也要尽量提出使用建议，以此来改进资源库的构建，在最大程度上发挥音乐资源库的作用。

(28)

仿真实验 1不同算法定位精度比较。本文算法、TLS算法和EKF算法在测量误差标准差σ为2°时的定位精度如图3所示。

可以看出,由于线性化误差较大,EKF算法并不收敛,本文算法的定位精度要优于TLS估计算法。

仿真实验 2不同算法运算时间比较。在本文算法滑窗长度t取10的情况下,本文算法、LS算法和TLS算法的运算时间如图4所示。

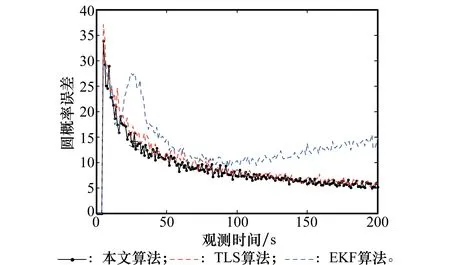
图3　不同算法定位精度比较Fig.3　Positioning accuracy comparison on different algorithm

图4　不同算法运算时间比较Fig.4　Operation time comparison on different algorithm

由仿真结果可知,观测时间小于40s时,3种算法的定位时间相差不大,随着观测时间的增加,TLS算法的运算时间呈指数增长,本文算法和LS算法基本呈线性增长,且本文算法的运算时间明显小于其他两者,由此可见本文的计算效率要高于TLS算法和LS算法。

仿真实验 3滑窗长度对算法定位性能的影响。在测量误差标准差σ为3°,观测时间为200s的情况下,滑窗长度对算法定位精度和运算时间的影响如图5和图6所示。

图5　滑窗长度对定位精度的影响Fig.5　Influence of sliding window length on positioning accuracy

图6　滑窗长度对运算时间的影响Fig.6　Influence of sliding window length on operation time

由仿真结果可以看出,滑窗长度越大,CEP的方差越小,运算时间越长。

图7　递推起始点对定位精度的影响Fig.7　Influence of recursive starting point on positioning accuracy

图8　递推起始点对运算时间的影响Fig.8　Influence of recursive starting point on operation time

由仿真结果可以看出,递推起始点的改变对CEP的影响呈现不规则性。递推起始越晚,运算时间越长。这是因为在递推起始之前,方程组的解均是由LS算法求得。结合定位精度和运算时间来看,递推起始应越早越好。

仿真实验 5平台与目标相对运动方向夹角对定位精度的影响。假设目标运动方向为y轴正半轴,初始位置为坐标轴原点,平台1与平台2运动方向与x正半轴的夹角分别为α1和α2,它们的取值范围均在0°～180°,初始位置分别为(30 000,0)和(-30 000,0)。在观测时间为200s时,算法得到的CEP如图9所示,它们之间的交会角即α1-α2的值如图10所示。

图9　相对运动夹角对定位精度的影响Fig.9　Influence of relative motion angle on positioning accuracy

图10　不同相对运动夹角时的交会角Fig.10　Cut angle of different relative motion angle

对比图8和图9可以看出,随着交会角α1-α2的增大,算法的定位精度逐渐降低。当α1的取值在0°～80°,α2的取值在90°～160°,且它们之间的差值在30°～150°,定位精度最高。结合它们的几何关系,此时平台1和平台2均是作远离目标航向的直线运动。

仿真实验 6不同平台速度对定位性能影响。平台速度v分别取150m/s、200m/s、250m/s时算法定位性能如图11所示。

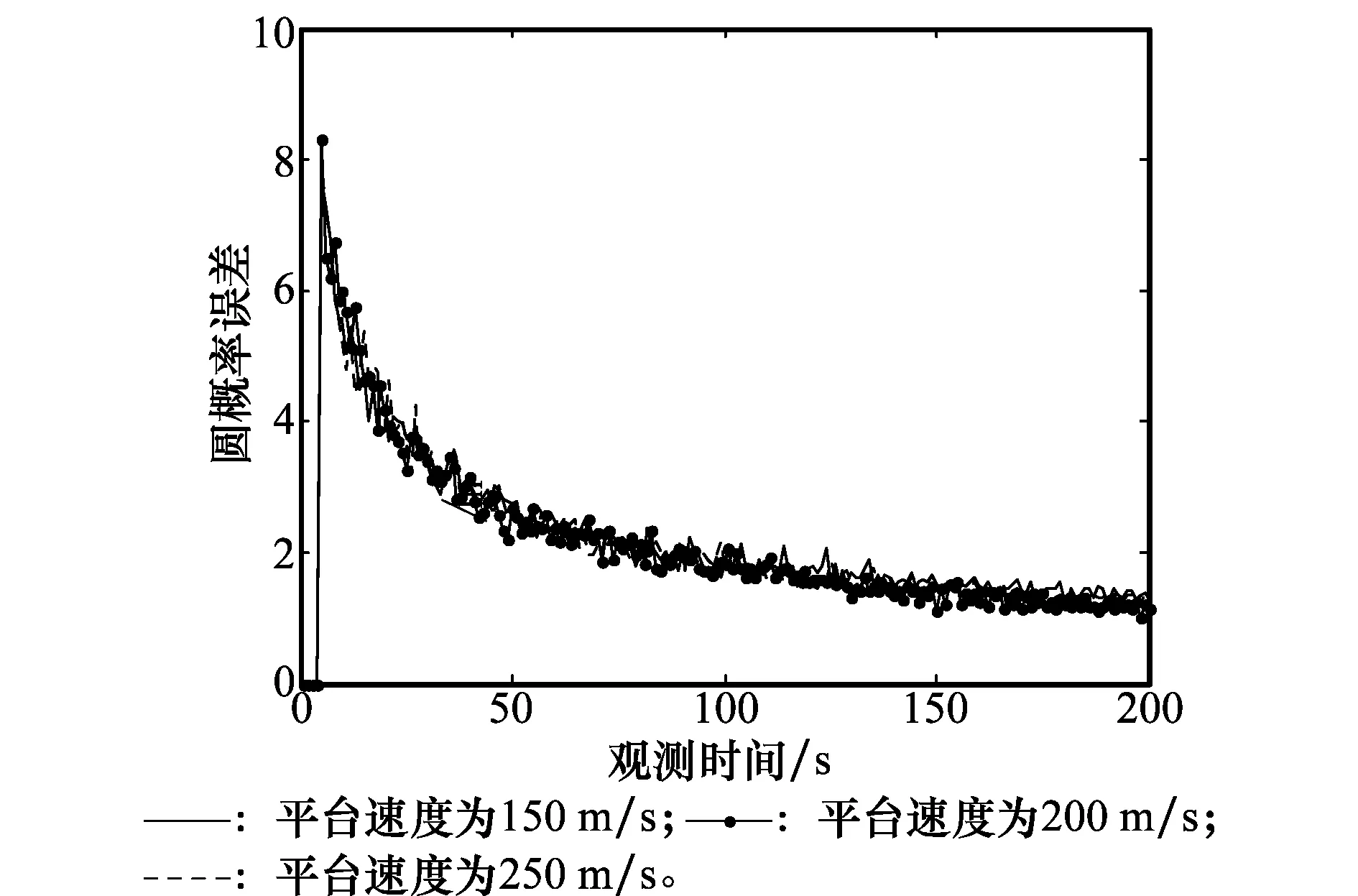
图11　不同平台速度下定位精度比较Fig.11　Positioning accuracy comparison on different movement speed of platforms

由仿真结果可以得出,平台速度对算法定位精度影响不大。

5　结　论

(1) 基于LS算法改进的滑窗式LS算法具有无偏性。在多平台测向定位系统中可以对目标进行高精度快速定位,不仅定位精度优于TLS算法和EKF算法,而且运算速度也要快于LS算法和TLS算法,在保证定位精度的前提下,可以大大减少定位时间。

(2) 滑窗长度越长定位精度越高,但运算量也随之增大,递推起始点的选择对定位精度没有明显的影响,但递推起始越晚,运算时间越长,在实际应用中,应结合实际情况选取滑窗长度和递推起始点。

(3) 双平台情况下,两个平台均做远离目标航向的直线运动时定位精度较高,它们之间的夹角越大,定位精度越高。

(4) 平台运动速度对定位精度影响不大。

[1]GharehshiranON,KrishamurthyV.Coalitionformationforbearings-onlylocationinsensornetworks-acooperativegameapproach[J].IEEE Trans.on Signal Processing,2010,58(8):4322-4338.

[2]WangSS,FengJF,LiQ,etal.Locationalgorithmfornearspaceradarnetworkbasedonangleinformation[J].Journal of Air Force Engineering University,2012,13(1):33-36.(王燊燊,冯金富,李骞,等.基于角度信息的近空间雷达网定位算法[J].空军工程大学学报, 2012, 13(1):33-36.)

[3]ZhangK,LiuY.Researchonpassivebearing-onlylocationalgorithmbasedonslowmovingtarget[J].Radar Science and Technology, 2014, 27(3):291-296. (张凯, 刘洋. 慢速目标仅测角无源定位算法研究[J].雷达科学与技术, 2014, 27(3):291-296.)

[4]WuSH,XinQ,WanJW.Observabilityanalysisofbearings-onlypassivelocationforsatellitetargetbyspacebornesingleobserver[J].Acta Aeronautica et Astronautica Sinica, 2009, 30(1):104-108. (吴顺华, 辛勤, 万建伟. 对卫星目标的仅测角天基单站无源定位可观测性分析[J].航空学报, 2009, 30(1):104-108.)

[5]DengY,HuXH,ZhangZZ,etal.Passivelocationaccuracyanalysisinbearing-onlyconstellationsystem[C]∥Proc.of the 3rd International Symposium on Systems and Control in Aeronautics and Astronautics, 2010: 1398-1402.

[6]HeY,GuanX,YiX.Researchontheun-observabilityproblemfortwodimensionaltrackingbasedonbearings-onlymeasurements[J].Systems Engineering and Electronics, 2003, 25(1):11-14. (何友, 关欣,衣晓. 纯方位二维运动目标的不可观测问题研究[J].系统工程与电子技术, 2003,25(1):11-14.)

[7]PoiselRA. Electronic warfare target location methods[M].London:ArtechHousePublishers, 2012: 147-189.

[8]XuZ,QuCW,WangCH.Performanceanalysisformultiplemovingobserverspassivelocalizationinthepresenceofsyste-maticerrors[J].Acta Aeronautica et Astronautica Sinica, 2013, 34(3):629-635.(徐征,曲长文,王昌海.系统误差条件下的多运动站无源定位性能分析[J].航空学报,2013,34(3):629-635.)

[9]GuoFC,SunZK,HanK.AmodifiedcovarianceextendedKalmanfilteringalgorithminpassivelocation[C]∥Proc.of the International Conference on Robotics, Intelligent System and Signal Processing,2003: 307-311.

[10]HeQY,ZhaoD.Algorithmofdirection-findinglocationonsingleairplanebasedonleastsquaremethod[J].Shipboard Electronic Countermeasure,2013,36(1):37-39.(何青益,赵地.基于最小二乘方法的单机测向定位算法[J].舰船电子对抗,2013,36(1):37-39.)

[11]MoCK,ChenSX,WuH,etal.Recursionleast-squarepassivelocationalgorithmbasedonangleinformation[J].Computer Measurement and Control,2014,22(9):2863-2866.(莫成坤,陈树新,吴昊,等.基于角度信息的递推最小二乘无源定位算法[J].计算机测量与控制,2014, 22(9):2863-2866.)

[12]WuH,ChenSX,ZhangHY,etal.Recursivetotalleastsquares-basedairbornesingle-observerpassivelocationalgorithm[J].Fire Control and Command Control, 2013, 38(6):19-22. (吴昊,陈树新,张衡阳,等.基于总体递推最小二乘的单站无源定位仿真分析[J].火力与指挥控制, 2013, 38(6):19-22.)

[13]AidalaVJ,NardoneSC.Biasedestimationpropertiesofthepseudo-lineartrackingfilter[J].IEEE Trans.on Aerospace and Electronic System, 1982, 18(4):432-441.

[14]HoKC,ChanYT.Anasymptoticallyunbiasedestimatorforbearings-onlytrackinganddoppler-bearingtargetmotionanalysis[J].IEEE Trans.on Signal Processing,2006,54(3):809-821.

[15]BertrandA,MoonenM.Consensus-baseddistributedtotalleastsquaresestimationinadhocwirelesssensornetworks[J].IEEE Trans.on Signal Processing, 2011, 59(5):2320-2330.

[17]GuanX,GuanX,TaoL,etal.Least-squarelocalizationalgorithmbasedonsingleplatforminslidingwindowway[J].Journal of China Academy of Electronics and Information technology,2015,10(5):557-562.(关欣,关欣,陶李,等.基于单机动平台的滑窗式最小二乘定位算法[J].中国电子科学研究院学报,2015,10(5):557-562.)

Unbiased algorithm of multiple platform passive location based on sliding window

GUAN Xin1, GUAN Xin1, TAO Li2, YI Xiao1

(1.NavalAeronauticalEngineeringAcademy,DepartmentofElectronicandInformationEngineeringYantai264001,China; 2.NavalAeronauticalEngineeringAcademy,AviationTrainingbaseQingdao266108,China)

To solve the problem that a single mobile platform cannot satisfy the system observability if it does not have a higher level movement than maneuvering target under bearings-only system, a passive location algorithm which is suitable for multiple mobile platforms is proposed. The algorithm based on the geometric relationships between the targets and platforms can get a pseudo linear system of equations including the initial position and velocity of target. To reduce the amount of calculation for solving system of equations and ensure real-time positioning, deal with the conventional least square method is deal with sliding window way, and the solution of equations is further expressed as the recursive form. Through the analysis of the observation vector and matrix of the equations, the unbiasedness of the algorithm is proved. Simulations experiments verify the effectiveness of the algorithm, the affections of the factors of platform motion such as speed and direction on the position performance of algorithm are discussed, and the relationship between the target and platforms that can obtain the position performance is gotten.

passive location; bearings-only system; least-squared (LS); multiple mobile platforms; sliding window way

2015-06-29；

2015-11-25；网络优先出版日期：2016-03-17。

教育部新世纪优秀人才支持计划(NCET-11-0872)资助课题

TN 957; TP 274

A

10.3969/j.issn.1001-506X.2016.09.03

关欣(1978-),女,教授,博士,主要研究方向为智能信息处理、多源信息融合。

E-mail:gxtongwen@163.com关欣(1990-),通信作者,女,硕士研究生,主要研究方向为无源定位。

E-mail:378887027@qq.com

陶李(1989-),男,硕士,主要研究方向为多源信息融合。

E-mail:290180440@qq.com

衣晓(1975-),男,教授,博士,主要研究方向为无线传感器网络、多源信息融合。

E-mail:yxgx_gxyx@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160317.1100.004.html