简述墩木变形与反力的计算方法

周上然

(海军上海地区装备修理监修室，上海 200000)



简述墩木变形与反力的计算方法

周上然

(海军上海地区装备修理监修室，上海 200000)

运用动力学软件ANSYS14.0建立墩木模型。分析了墩木弹性模量、高度和接触面积对墩木变形的影响；计算了一艘实船在艉倾状态下艉墩木反作用力以及稳性的变化；利用弹性基础梁模型，计算了艉墩木和舯部墩木的变形及艉墩木的布置位置。

墩木变形；墩木反力；弹性基础梁

0　引　言

船舶在进坞坐墩时，墩木反作用力会逐渐增大，并会对船舶的稳性产生一定影响。因此，必须对坞墩的强度进行校验，在保证坞墩强度的同时，考虑坞墩反力对船舶稳性的影响。坞墩反作用力和船舶稳性均与吃水和浮态有关，在船舶进坞之前要结合船体结构强度确定船舶的浮态和吃水。这里简化坞墩模型，不考虑坞墩钢架和坞底的变形，假定其为刚性，只考虑墩木变形及其反作用力。

1　墩木变形

坞墩上与船体直接接触的部分是墩木，当墩木受到横向压力(即横纹压缩)时，其细胞横断面会发生变形[1]。木材变形会随着施加压缩载荷的增大不断增大，一旦载荷超过墩木材质的弹性极限，木材的外表面纤维及其附近纤维就会遭到破坏，变得相对紧密，形成固定变形。由于压缩载荷是直接作用在墩木外表面的，外表面纤维遭到的破坏最严重，破坏形式较为明显，由外表面向内表面受到的压缩和破坏程度不断减小。

木质构件具有重新分配应力和吸收能量的能力。假设木材是连续且密度均匀的，没有任何生长缺陷。从木质构件中任意取一部分，不论体积大小，其应力与应变的关系及载荷与变形的关系均可用连续函数表达，其密度和弹性常数均不随位置坐标的变化而变化。若木材是线弹性的，则在外载荷作用下应力和应变服从胡克定律。当外加载荷消失后，没有任何残余变形出现。

在墩木强度设计因素中，要充分考虑可能遇到的客观条件对其强度的影响。根据标准，在对木质构件进行强度校核时，要对其强度进行一定的折减，折减后的强度值称为许用应力，即木质构件在使用寿命期内或承受一定外载荷时所能长期、安全地承受的最大应力。相对于金属材料，木质构件的安全系数取值较高，一般取3.5～6。

墩木本身的变形(因自身重力产生的变形)相对于其原始尺寸是非常小的，可不用考虑。墩木材质为正交各向异性，具有3个相互垂直的弹性模量。根据经验数据，Ex∶Ey∶Ez=10∶1∶0.5，x为墩木长度方向，y为墩木宽度方向，z为墩木高度方向。利用ANSYS14.0软件建立龙骨墩与边墩模型(见图1)，龙骨墩为立方体形状，墩木的底面施加固定约束，施加垂直于外表面的均匀压缩载荷(沿高度方向)。模型的参数设置及最大变形见表1，变形图见图2。模型1、模型2、模型3施加的压缩载荷为2 MPa；模型4和模型5施加压缩载荷分别为1.8 MPa和1.5 MPa，对应应力图见图3，外表面最大应力分别为4.1 MPa和3.3 MPa。

图1　墩木的数值模型

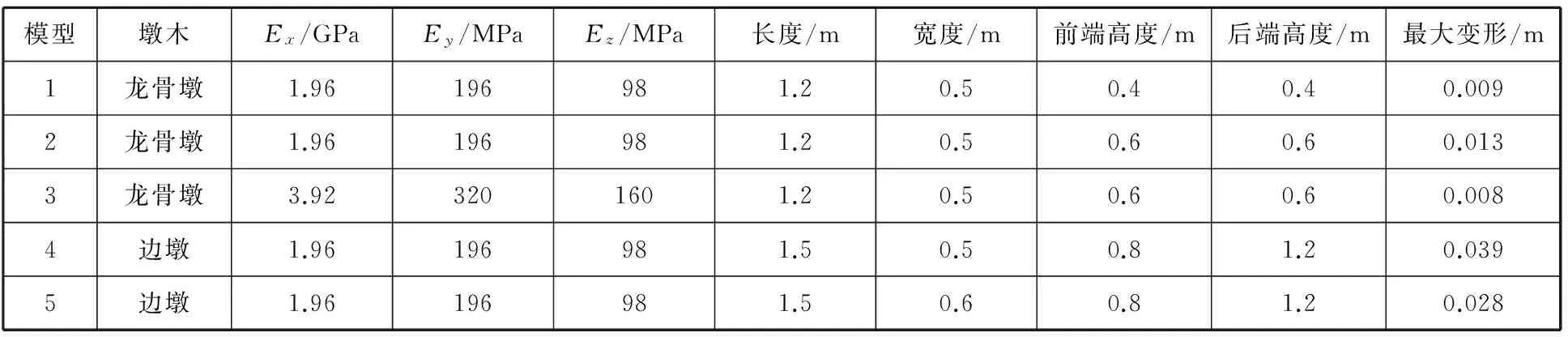
模型墩木Ex/GPaEy/MPaEz/MPa长度/m宽度/m前端高度/m后端高度/m最大变形/m1龙骨墩1.96196981.20.50.40.40.0092龙骨墩1.96196981.20.50.60.60.0133龙骨墩3.923201601.20.50.60.60.0084边墩1.96196981.50.50.81.20.0395边墩1.96196981.50.60.81.20.028

a) 模型1

b) 模型2

c) 模型3

d) 模型4

e) 模型5

b) 模型5

从图2中可看出，外表面的变形量最大，从外向内依次减小，与木材压缩理论相符。对比表1中模型1和模型2的数据可以看出，当墩木的高度增加时，其外表面最大变形量增大。因为随着高度增加，刚性系数K减小，在外部载荷不变的情况下变形增大。

(1)

对比表1中模型2和模型3的数据可知，在相同尺寸和外载荷条件下，提高墩木材质的弹性模量，刚性系数K会随之增大，最大变形量明显减小。对比表1中模型4和模型5的数据可知，在相同的坞墩反作用力作用下，增大接触面积可减小压强、降低墩木的压缩应力和内应力；同时，刚性系数K变大，最大变形量减小。边墩的最大变形位置在外表面的边缘处，工程实践中，受墩木高度误差及船体变形等因素影响，墩木与船体不能完全贴合，会对墩木的强度产生影响，因此需要在间隙处加垫木楔。从经济性的角度出发，增大面积会增加墩木的消耗量，受舭部型线和水下工程的限制，边墩面积不能增大太多。

2　墩木反力

船舶在坞内坐墩时，其位置会随着坞内水位的降低而不断下降。若船舶处于艉倾状态，则船尾会最先接触到尾坞墩，该过程可分为以下4个阶段。

1) 第一阶段：船舶保持进坞时的浮态不变，下降速度较为缓慢，直到船尾刚刚接触艉墩木。在此阶段，船体承受的重力和浮力大小相等，处于平衡状态，墩木对船体没有作用力。

2) 第二阶段：船尾刚接触到艉墩木，以两者的接触线为轴，整个船体绕轴转动，直至船首接触到墩木，稳定地坐墩；即从艉倾状态变为水平状态，艏艉吃水相同。在该阶段，船舶承受重力、浮力和坞墩的反作用力；重力大小等于浮力与墩木的反作用力之和。随着坞内水不断减少，浮力减小，坞墩反作用力不断增大；与此同时，船体的稳性高也会随之发生变化。在船体完全坐墩之前，减少的那部分浮力是由艉墩木反作用力补偿的，因此要校核艉墩木的强度及因坞墩反作用力造成初稳性高的变化量。对于墩木反作用力的校核，该阶段最为重要。

实际工程中，测得艉墩木反作用力开始是增大的，增大到某一数值后开始变小。因为开始只有1个墩木与船体接触，此时艉墩木的反作用力不断增加；随着纵倾不断减小，受船体型线变化的影响，艉部接触的墩木数量逐渐增加；此外，边墩的钢架高度往往高于龙骨墩的钢架高度，船体会先接触到边墩，这也会降低艉墩木的受力，因此墩木反作用力开始减小。

官厅水库黑土洼湿地系统2016年水质监测评价分析……………………………………… 杨垒，吴玉欣，王彦芹（3-137）

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

经计算，pmax=252.9 t，相对于工程实际，数值偏大。由以上各式可看出：艉墩木反作用力与船体纵倾值有关，在小角度情况下两者呈线性关系；此外，墩木反作用力降低了船体的初稳性。船舶进坞时一般处于艉倾状态，可通过适当减少艉部的压载或增加艏部的压载来减小艏艉吃水差，以达到降低坐墩反作用力的目的。

3) 第三阶段：从船体稳定坐墩开始，到坞内水降至船底以下为止，船体的浮力在这阶段完全消失，由墩木支撑船体重量。船体只承受重力与墩木反作用力，两者大小相等，处于平衡状态。墩木反力的大小分布取决于墩木的刚性系数、布置数量、接触面积及间距等因素。

4) 第四阶段：坞内水完全排干，坞墩的浮力消失，该阶段主要会对坞底产生一些影响，对船体的受力影响不大。

在实际坐墩过程中，边墩亦承受部分重力，降低了龙骨墩上的坐墩反作用力和船舶龙骨的受力。根据承受载荷的统计资料，同一肋位处，龙骨墩的受力比例为67%～70%，边墩的受力比例为40%～43%，但受船舶型线的约束，两者要在变化平缓处布置。可将边墩反作用力分解为对船体的水平力和垂直力，即

(10)

(11)

(12)

式(10)～式(12)中：中为边墩反作用力；为边墩的倾斜度；B1为边墩布置的横向距离；φ为横倾角。从式(12)中可看出，边墩布置的横向距离一般取较大值，这样可提高船舶的稳性；同样，船舶在艉倾状态下，也会对艉墩产生一个侧推力。因此，要对艉墩和边墩采取固定措施，通常采用角钢将各个墩木的钢架焊接成一个整体。

3　墩木布置

通常，墩木简化为连续的弹性基座，将船体简化为一根连续的变截面惯性矩的弹性基础梁，艏艉两端变化较大，中间段变化较小，可近似取为固定值，艏艉悬伸端(重量)对墩木的影响等效为作用在艏艉墩木处的集中力和弯矩。整个船体梁承受着重力和弹性基础梁的反作用力(坞墩反作用力)。从重量分布的规律来看：舯部重量分布较大，因此该处的墩木受力较大，布置的墩木数量应适当增加，以控制墩木的反作用力；此外，因为舯部型线变化不大，船体面积较大，可增加边墩数量。船首声呐导流罩接触面积较小，容易导致受力集中，且型线变化较大，不宜布置墩木。一般选择在型线变化较缓且接触面积较大的部位布置墩木，艏墩木承受着船首所有的重量，因此墩木的尺寸要适当增大一些，布置的间距要适当紧凑一些。同样，船尾还要考虑螺旋桨的影响，选择在平缓且接触面积大的地方布置墩木。弹性基础梁反作用力(墩木反作用力)与墩木的刚性系数、布置的墩木数量、船舶横向截面惯性矩及艏艉墩木的纵向间距等因素有关。

布置的墩木数量取决于船舶的坐墩重量、墩木的屈服强度、墩木与船体的接触面积及载荷分布的不均匀系数[3]。

(13)

(14)

式(13)、式(14)中：D为坐墩时船舶的装载；KH为载荷分布不均匀系数；Rpacy为坞墩的计算强度；SΔoy为所有墩木与船体的接触面积，S单个墩木的面积。

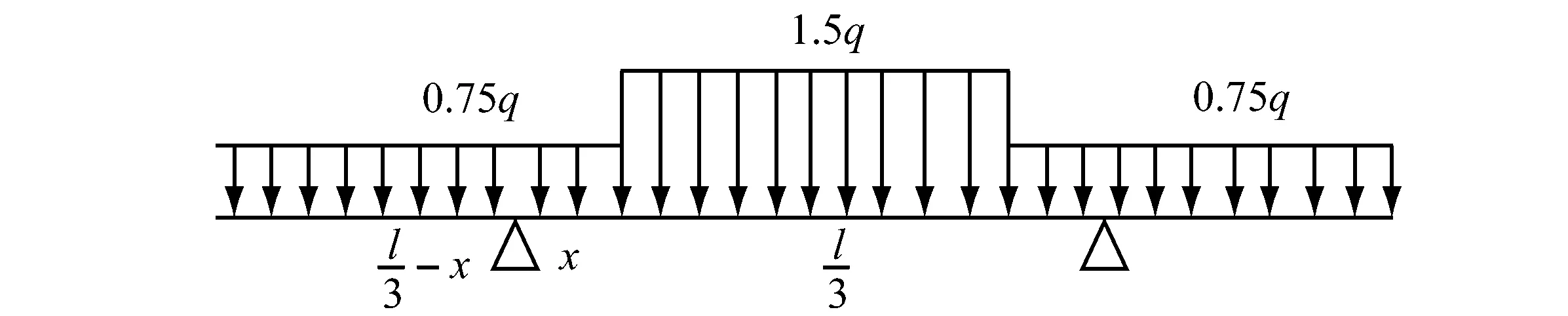
假设各个龙骨墩表面是水平的，承受着船舶的全部重力。由于载荷沿船长方向的分布是不均匀的，因此不同位置处坞墩的变形不同。平行中体部分船体的扰度主要是由分布载荷引起的，可简化为无限长弹性基础梁；艏艉两端的坞墩除受到分布载荷以外，还会受到集中力和力矩的作用，产生附加扰度；艉部可简化为两端自有支持的半无限长弹性基础梁，一端单向固定的半无限长弹性基础梁[4]，位移计算公式如式(15)和式(16)[5]，第一项为等效弯矩引起的位移，第二项为等效力产生的位移。假设弹性基础梁刚性系数k为常数，艏部、舯部和艉部的长度均为l/3，l为船长，舯部横截面惯性矩为2I，艏艉段横截面惯性矩为I，载荷分布见图1，艏艉端均布载荷为0.5q，舯部均布载荷为1.5q。

(15)

(17)

在艉墩处，等效弯矩产生的位移可改写为

(18)

(19)

(20)

等效力产生的位移可改写为

(21)

(22)

将k=98 MPa、E=210 GPa、I=1.5×108cm4、l=110 m及x=20 m代入式(15)和式(16)，可得：

(23)

(24)

从计算结果中可看出：艉墩木的变形量相对于中间墩木要大，这主要是因为艉部悬伸端起了一定作用。布置艉墩时应尽量减小船尾悬臂长度，以减轻附加力与力矩，但是船尾悬臂过短或艏艉墩木跨度过长会导致

舯部弯矩增大，因为舯部弯矩与两端点之间的跨度成正比。以两端点梁支撑为例，当支点处的弯矩M0与舯部的弯矩M1相等时，该支点为最佳位置。

(25)

(26)

(27)

船尾悬伸端长度为

(28)

实际上，受弹性基础梁的影响，舯部的弯矩值可适当减小，艏艉墩木的跨度可增大。

4　结　语

1) 在船体坐墩力作用下，墩木外表面的变形最大；在墩木反作用力相同的情况下，提高墩木的弹性模量或增大墩木的接触面积，墩木的最大变形量减小；增大墩木的高度，墩木的最大变形量增大。

2) 若忽略船底型线变化(完全平底)和墩木高度变化(完全水平)，则计算出的墩木反力偏大；受船底型线变化和墩木高度的影响，墩木反作用力先增大后减小。

3) 艉墩木的变形量相对于中间墩木要大，主要是因为艉部悬伸端起了一定作用。在艉倾状态下，墩木反作用力更大，因此要对艉墩木进行强度校核，同时要防止对墩木上的船底结构造成损坏。可通过提高墩木的弹性模量、增加墩木的接触面积提高墩木的许用强度，或降低艉墩反作用力，即减小船体进坞纵倾。

[1]徐有明.木材学[M].北京: 中国林业出版社，2006.

[2]盛振邦，刘应中.船舶原理[M].上海:上海交通大学出版社，2003.

[3]王福花,朱云翔，王维. 大型舰船坐坞强度衡准与计算方法.[J].中国造船, 2008,49(3):83-90.

[4]张寿富,朱小龙.船舶布墩的理论和实践[J]. 江苏船舶, 1995,12(3):19-22.

[5]林砚田. 半无限长弹性基础梁的通用计算公式[J]. 华中工学院学报，1977(3)：108-124.

Introduction to Calculation of the Deformation and Counterforce of Wooden Blocks

ZHOU Shangran

(TheSupervisionDepartmentofNavyEquipmentRepairintheShanghaiArea,Shanghai200000,China)

The model of wooden blocks for analyzing the influences of the wood elastic modulus, the height and the contact area on the deformation of wooden blocks are built with the dynamic software ANSYS14.0; The stability of a ship on blocks with trim by stern and the counterforce of wooden blocks are calculated; The deformations of the wooden blocks at the middle and at the last back are calculated with the elastic foundation-beam model; The layout of the last back wooden blocks are proposed.

deformation of wooden blocks; counterforce of wooden blocks; elastic foundation-beam

2016-01-11

周上然(1987—)，男，江苏建湖人，工程师，主要从事船舶装备修理质量监督工作。

1674-5949(2016)01-016-05

U661

A