模型预测控制在MMC-HVDC中的应用

梁营玉　张　涛　刘建政　杨奇逊　梅红明　刘　树

（1.新能源电力系统国家重点实验室（华北电力大学） 北京　102206 2.北京四方继保自动化股份有限公司　北京　100085 3.电力系统及发电设备控制和仿真国家重点实验室（清华大学） 北京　100084）

模型预测控制在MMC-HVDC中的应用

梁营玉1张涛2刘建政3杨奇逊1梅红明2刘树2

（1.新能源电力系统国家重点实验室（华北电力大学） 北京102206 2.北京四方继保自动化股份有限公司北京100085 3.电力系统及发电设备控制和仿真国家重点实验室（清华大学） 北京100084）

针对不对称交流电网下模块化多电平换流器型高压直流输电系统（MMC-HVDC）的传统不平衡控制策略存在的诸多缺点，提出两种改进的不平衡控制方法：电流环模型预测控制方法和模型预测直接功率控制方法。两种方法分别实现了对MMC交流侧电流的控制和对MMC交流侧有功和无功功率的直接控制。详细描述了两种控制方法的控制原理及设计过程，与传统的双矢量控制策略从控制结构复杂度、稳态性能和动态性能等方面进行了对比分析。将模型预测直接功率控制与功率补偿策略相结合，以分别实现不对称电网下抑制负序电流、抑制有功波动和抑制无功波动3种控制目标。在PSCAD/ EMTDC中搭建了5电平MMC-HVDC模型，验证了该文所提两种控制方法的正确性和有效性。

模块化多电平换流器模型预测控制直接功率控制双矢量控制不对称电网电压

0　引言

模块化多电平换流器（Modular multilevel converter，MMC）作为一种新型的电压源型换流器拓扑［1］，可进行模块化设计，可扩展性好，通过增加或减少串联子模块的数量，可灵活地改变应用的电压等级［2］。与传统两电平或三电平电压源换流器（Voltage Source Converter，VSC）相比，MMC开关频率较低、输出电流的谐波含量少以及对电力电子开关的一致性要求较低［3，4］，在高压直流输电领域具有广阔的应用前景。

电网交流输电线路运行时，可能因为各种原因而发生接地故障，其中单相接地故障占绝大多数，导致电网三相电压不对称。因此，研究用于直流输电的MMC不对称电网下的控制策略对于提高MMC在电网故障时的运行能力具有重要意义。基于PI调节器的双矢量控制策略是一种常用的不平衡控制策略。在电网电压不对称时，双矢量控制策略［5］需要采用正负序两套旋转坐标变换，分别将正负序电流转换为直流量，然后采用PI调节器进行控制。该方法控制结构复杂，需要调整的PI参数较多，控制效果受PI参数的影响，且正负序分解环节引入的延时降低了系统的动态性能和稳定性［6］。文献［7，8］提出αβ静止坐标系下的比例谐振（Proportional Resonance，PR）调节器。PR调节器可同时控制正负序电流，从而避免了反馈电流的正负序分解。然而，该方法的控制性能受PR参数的影响，只有选择合适的PR参数才能获得满意的控制效果。

模型预测控制（Model Predictive Control，MPC）自被提出以来，已在过程控制领域获得了广泛应用。随后，智利学者J.Rodriguez在传统的模型预测控制基础上提出了适用于电力电子领域的有限控制集模型预测控制（Finite Control Set MPC，FCS-MPC；若无特殊说明，本文所提的模型预测控制均特指FCS-MPC）。近年来，已有学者将其应用于PWM整流器［9］、交流电机控制［10］、UPS［11］以及矩阵换流器［12］，并取得了一定的研究成果，然而模型预测控制应用于MMC的研究成果鲜有报导。

针对不对称交流电网下传统的MMC控制策略存在控制结构复杂、需要调整的PI参数较多以及动态响应速度较慢等缺点，本文基于模型预测控制器提出两种改进的控制方法:电流环模型预测控制方法和模型预测直接功率控制方法。第一种改进方法是在αβ坐标系下采用模型预测控制器对正负序电流进行统一控制，避免了对反馈电流做旋转坐标变换和正负序分解，无需复杂的PI参数整定，简化了控制结构，并提高了动态响应速度。第二种改进方法是基于不对称电网电压下的功率模型，采用模型预测控制器对MMC交流侧有功和无功进行直接控制，省略了电流内环。在PSCAD/ EMTDC中搭建了相应的仿真模型，对所提控制方法进行了验证，并与双矢量控制策略进行了仿真对比。

1　MMC拓扑结构与数学模型

MMC单相电路如图1所示。单相MMC由上下两个桥臂组成，每个桥臂由N个完全相同的半桥子模块与桥臂电感串联而成。3个完全相同的单相MMC组成三相MMC。图1中，usk和isk分别为交流电压和交流电流（k=a，b，c）；Lr和Rr分别为桥臂电感和桥臂等效损耗电阻；udc和 idc分别为直流电压和直流电流；upk、unk和ipk、ink分别为桥臂电压和桥臂电流（p代表上桥臂，n代表下桥臂）。桥臂电抗器直接串联在桥臂中，可抑制直流侧短路时的故障电流上升率，提高电力电子器件的安全性。

图1　MMC单相电路Fig.1　Single-phase MMC circuit

根据MMC电路结构及基尔霍夫定律，可推导MMC交流侧的数学模型［4］为

式中，vk为MMC第k相输出电压，其表达式为

在αβ两相静止坐标系下，式（1）可表示为

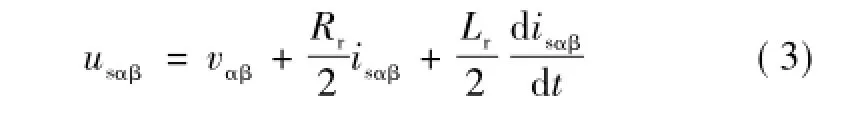
在交流电网不对称情况下，电压、电流可分解为正序分量和负序分量，因此式（3）可分解为

式中，上标“+”代表正序分量；上标“-”代表负序分量。

式（4）、式（5）分别在正序和负序旋转坐标系下可表示为

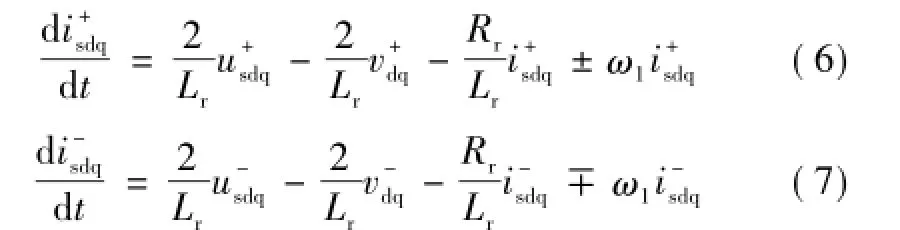
式中，ω1为电网角频率。

2　不对称电网电压下MMC传统控制方法

MMC交流侧的传统控制方法由参考电流的计算环节和内环电流跟踪环节组成。

2.1参考电流计算

电网电压不对称时，MMC交流侧瞬时有功和无功可表示为［4，13，14］

式中，P0、Q0分别为瞬时有功和无功的平均分量；Pcos2、Psin2分别为瞬时有功2倍频波动分量；Qcos2、Qsin2分别为瞬时无功2倍频波动分量。各分量的表达式为

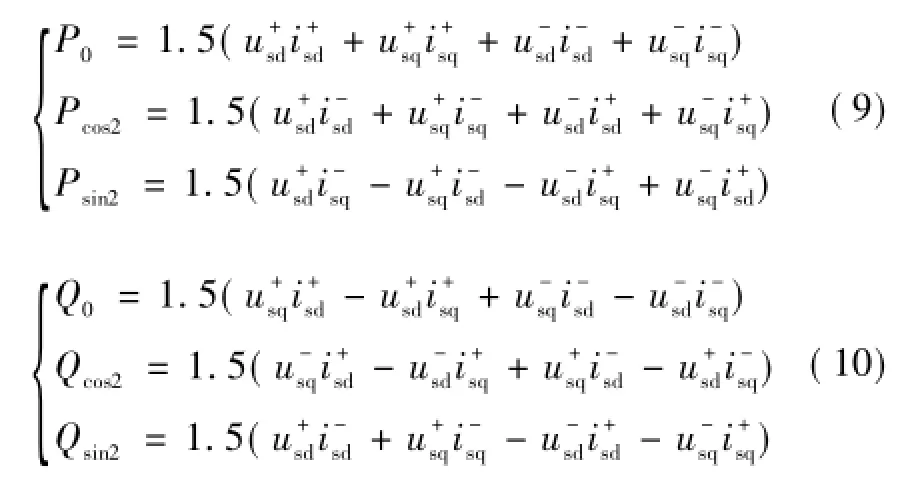
针对电网电压不对称时，MMC交流侧出现的三相电流不平衡、有功波动和无功波动等异常情况，MMC具有以下3种可选择的控制目标［14］。

控制目标2:抑制有功2倍频波动分量，即Psin2= Pcos2=0，由式（9）、式（10）得

式中

控制目标3:抑制无功2倍频波动分量，即Qsin2= Qcos2=0，由式（9）、式（10）得

2.2双矢量控制策略

在电网不对称故障下，正负序分量分离后可得到式（4）所示的正序数学模型和式（5）所示的负序数学模型。正序数学模型和负序数学模型在相应的正序和负序旋转坐标系下，所有变量均为直流量（式（6）和式（7）），因此可采用PI调节器对正序和负序分量分别调节，于是，可得MMC正负序指令电压分别为

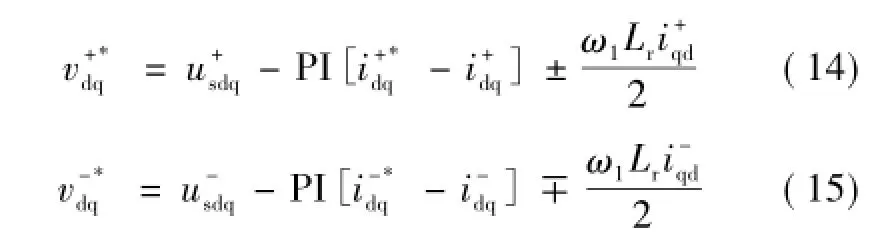
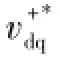
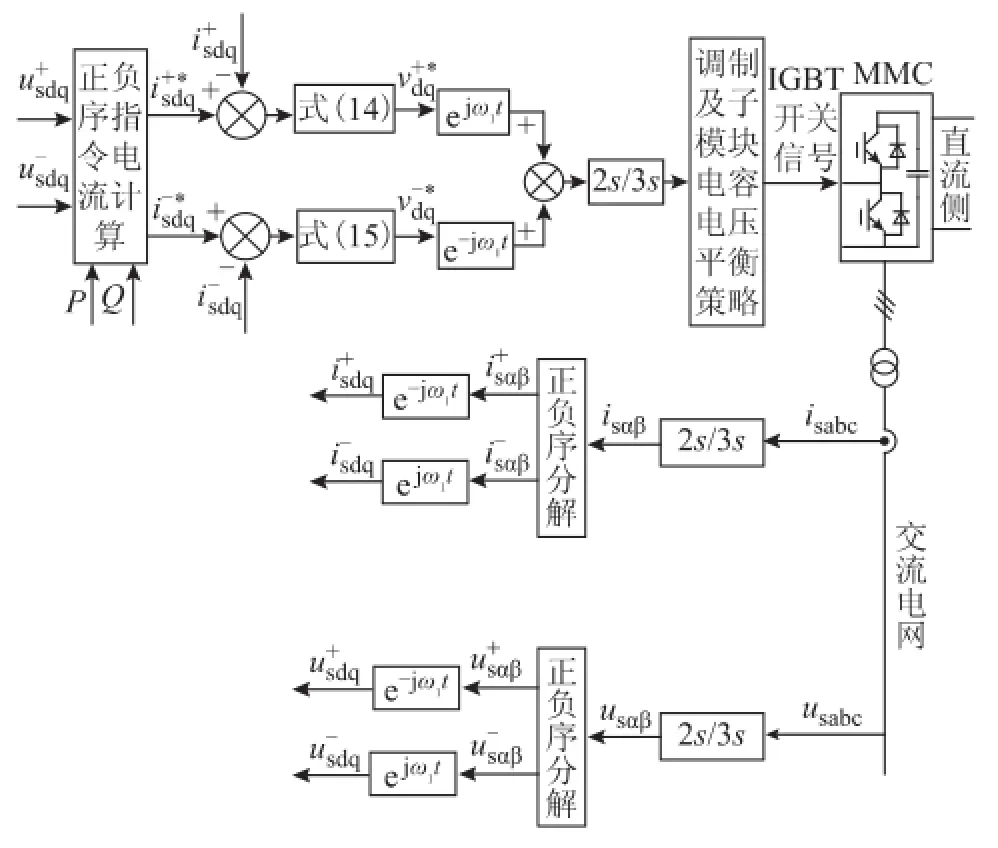
图2　不对称电网电压下MMC传统控制策略Fig.2　Traditional control strategy for MMC under asymmetry grid voltage

3　电流环模型预测控制

虽然基于PI调节器的双矢量控制策略在不对称电网电压下能取得较好的稳态控制效果，但需要对反馈电流isαβ进行正负序分解，正负序分解引入的延时将降低电流跟踪环节的动态性能及稳定性。此外，电流跟踪环节需采用4个PI调节器对正负序电流的d轴、q轴分量分别控制，结构复杂且需要调整的参数较多。为此，本文采用模型预测控制代替双矢量控制策略进行参考电流的跟踪。值得一提的是，与双矢量控制策略的电流参考值计算方法相同，电流环模型预测控制的电流参考值也是根据2.1节的相关公式计算得到。

采用一阶前向差分法将式（3）离散化，可得到MMC离散数学模型为

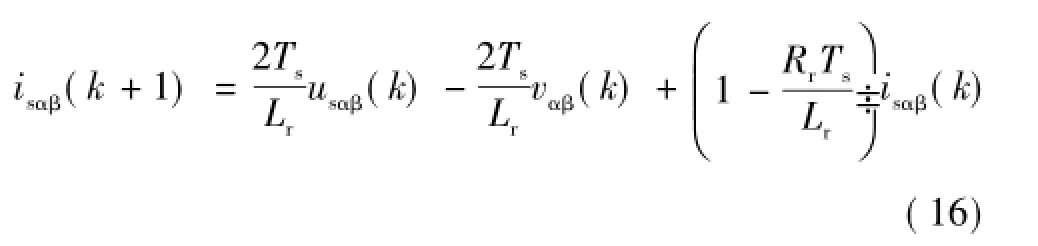
式中，k为kTs时刻的采样值；k+1为（k+1）Ts时刻的预测值；Ts为采样周期。

不考虑内部环流，MMC上下桥臂电压满足

由式（2）、式（17）可得

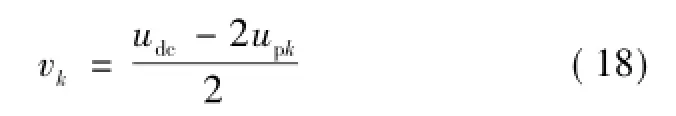
假设在电容电压平衡控制策略下，各桥臂子模块电压保持相等［15］，上桥臂投入的子模块数量介于0到N之间，则

MMC每相输出电压具有N+1种可能的电平数va（k），vb（k），vc（k）∈

则三相MMC输出电压vabc（k）具有（N+1）3种可能的组合。对vabc（k）进行克拉克变换得到vαβ（k），由式（16），根据kTs时刻各电气量的采样值以及控制量vαβ（k）可预测（k+1）Ts时刻的电流。为了实现参考电流的跟踪，定义如下目标函数

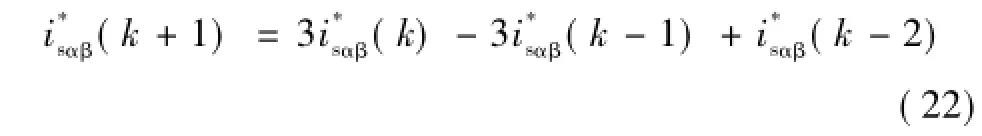
图3　电流环模型预测控制流程图Fig.3　Flow chart of current loop model predictive control

模型预测控制可直接在αβ坐标系下实现对参考电流的跟踪，不需要对反馈电流进行旋转坐标变换和正负序分量的分解，降低了控制复杂度，同时改善了控制系统的动态性能。此外，采用模型预测控制不需要进行复杂的PI参数整定，并且相对于PI调节器，MPC具有更好的参数鲁棒性［10］。

4　模型预测直接功率控制

相对于基于双矢量控制的传统方法，基于电流环模型预测控制的MMC交流侧控制策略具有诸多优势，但其控制结构仍由参考电流计算环节和电流跟踪环节组成，控制结构仍略显复杂，无法实现对交流侧功率的直接控制。于是，本节基于MMC交流侧功率模型提出一种可直接控制MMC交流侧有功和无功的模型预测直接功率控制策略（Model Predictive Direct Power Control，MPDPC）。

4.1不对称电网电压下MMC功率模型

将式（1）改写为矢量形式为

式中，Us、V、Is均为矢量，可定义为

交流电网不对称时，电压、电流可分解为正序和负序分量，如下

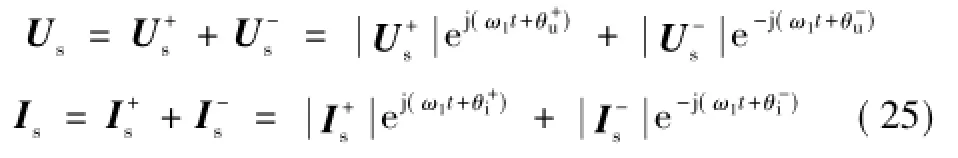
根据瞬时功率理论［16］，MMC交流侧瞬时复功率可表示为

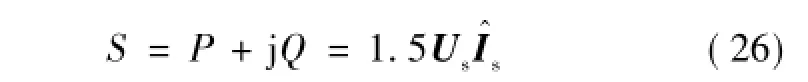
复功率对时间t的变化率为

由式（25）电压矢量的表达式可得电压矢量的导数为

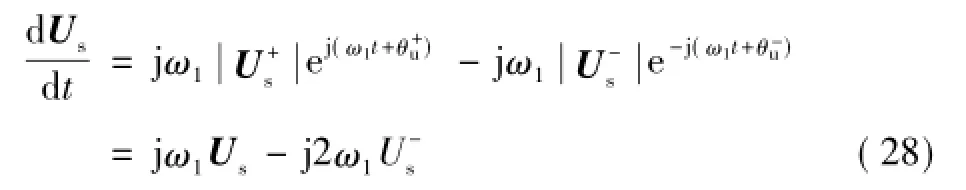
将式（23）和式（28）代入式（27）可得

式（29）为MMC交流侧功率模型。理想电网下，不存在负序电压即U-s=0，将其代入式（29）即得到理想电网下的功率模型。

将式（29）分解为实部和虚部的形式可得

4.2不对称电网电压下功率分析

将式（25）代入式（26），并进行整理可得瞬时有功和瞬时无功的表达式为［17］

式中

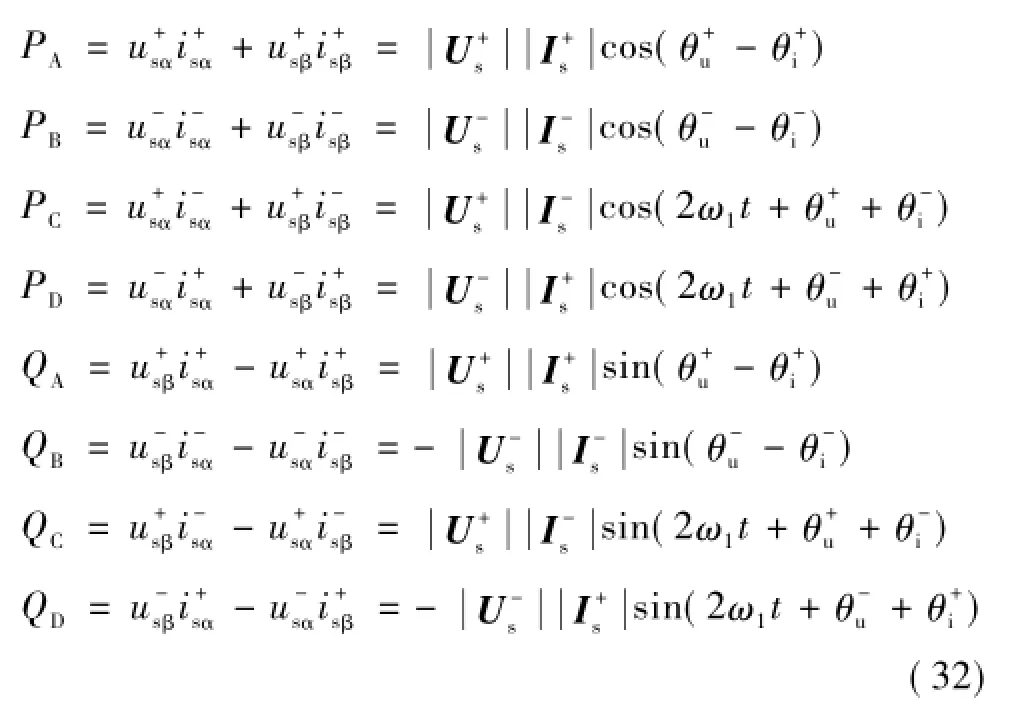
由式（32）可看出，PA、PB、QA、QB分别为电压与电流同序分量相互作用产生的直流功率分量；正序电压和负序电流相互作用产生2倍频功率波动分量PC、QC；负序电压和正序电流相互作用产生2倍频功率波动分量PD、QD。理想电网下不存在负序电压和负序电流，因此只有功率分量PA和QA。正负序电压和电流矢量的空间关系如图4所示。从图中可清楚地看出，同序电压矢量和同序电流矢量相对静止，因此产生的功率分量PA、PB、QA、QB均为直流量；不同序电压矢量与电流矢量旋转的相对角速度为2ω1，因此PC、PD、QC、QD均为2倍频波动分量。

图4　电压、电流矢量空间关系示意图Fig.4　Schematic diagram of spatial relationship between voltage and current vectors

4.3不同控制目标下功率参考值的计算

在不对称电网电压下，需要根据不同的控制目标在原始的功率参考值的基础上增加相应的功率补偿分量以得到新的功率参考值［18-20］。

1）控制目标1:抑制负序电流

目标1为抑制负序电流，使三相电流平衡，以避免电力电子器件过电流。为了抑制负序电流，应使与负序电流相关的功率波动分量PC、QC为零，即

2）控制目标2:抑制有功波动

电网电压不对称时，由式（31），瞬时有功将存在波动分量PC和PD，为了抑制有功波动，令PC+PD为零，即

控制目标2对无功功率未作任何要求，因此，无功功率将保留波动分量QC、QD，即在原始的无功功率参考值Qconst基础上增加补偿分量QC+QD，则新的功率参考值为

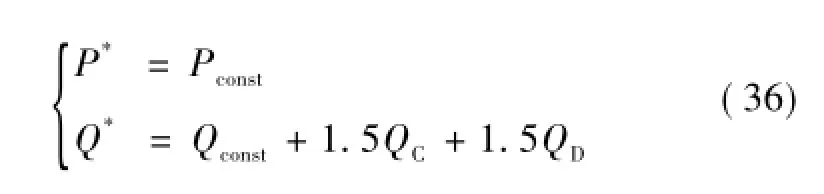
将式（32）中PC和PD的表达式代入式（35）可得

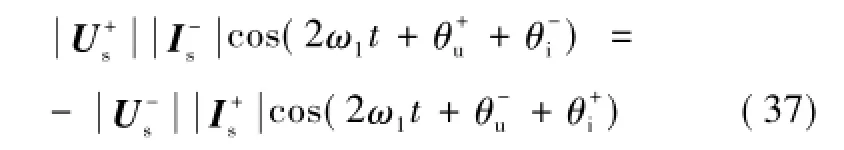
由式（37）可推导出如下关系式

将式（38）代入式（32）可得

因此，功率参考值P*、Q*可改写为

3）控制目标3:抑制无功波动

电网电压不对称时，由式（31），瞬时无功将存在波动分量QC和QD，为了抑制无功波动，令QC+QD为零，即

控制目标3对有功功率未作任何要求，因此，有功功率将保留波动分量PC、PD，即在原始的有功功率参考值Pconst基础上增加补偿分量PC+PD，则新的功率参考值为

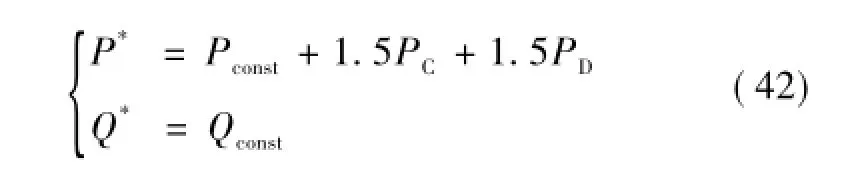
将式（32）中QC和QD的表达式代入式（41）可得

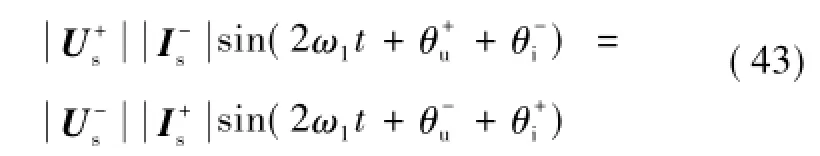
由式（43）可推导出如下关系式

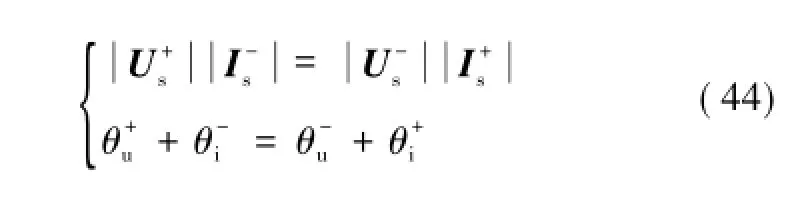
将式（44）代入式（32）可得

将式（45）代入式（42），功率参考值P*、Q*可改写为

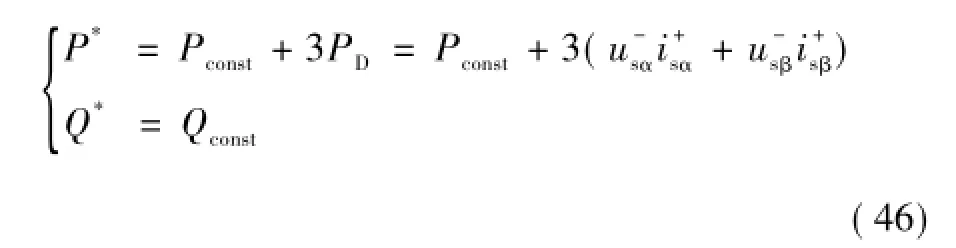
4.4模型预测直接功率控制

采用一阶前向差分法将式（30）离散化可得功率预测模型

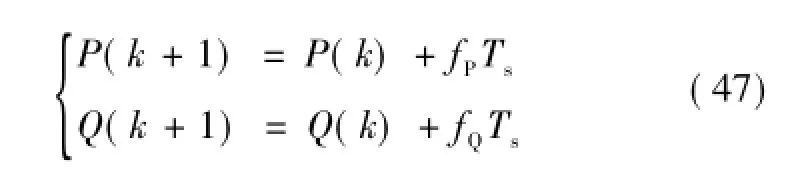
由式（30），电网电压矢量Us和电流矢量Is均为扰动量，有功和无功的变化率fP和fQ由MMC的输出电压矢量V决定。因此，通过改变V的大小可实现对有功和无功功率的直接控制，不需要电流跟踪环节。

为减小有功、无功与其参考值的误差，构造如下目标函数

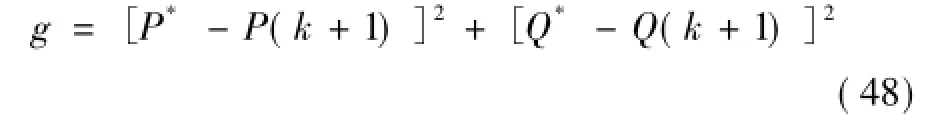
根据第3节的相关分析，MMC输出电压va、vb、vc均具有N+1种可能的输出电平，因此，根据MMC输出电压矢量V的定义（式（24）），电压矢量V具有（N+1）3种可能性。

不对称电网电压下模型预测直接功率控制原理框图如图5所示。首先测量电网电压矢量Us和电流矢量Is，并根据式（26）计算MMC交流侧瞬时有功和无功功率，即P（k）、Q（k）；然后根据功率预测模型（式（47））及所有可能的MMC输出电压矢量V预测下一时刻的有功和无功功率，即P（k+1）、Q（k+1）；基于功率参考值 P*、Q*和功率预测值 P（k+1）、Q（k+1），计算目标函数值；选出使目标函数最小化的MMC输出电压矢量Vmin即为下一控制周期MMC的调制电压。由于每个控制周期都是以预测功率与参考功率之间误差最小为目标选取MMC应输出的电压矢量，因此，可实现对功率参考值的精确跟踪。

不对称电网电压下，MPDPC虽然需要进行功率参考值的计算，但与采用传统的双矢量控制和电流环模型预测控制时的参考电流计算相比，计算公式相对简单。此外，MPDPC省略了电流内环，因此，不需要PI调节器及相应的参数整定过程，可实现功率的直接控制，响应速度快。

图5　不对称电网电压下MMC模型预测直接功率控制Fig.5　Model predictive direct power control for MMC under asymmetry grid voltage

5　仿真结果与分析

为验证本文所提电流环模型预测控制和模型预测直接功率控制的正确性和有效性，并将本文中提到的3种不对称电网电压下MMC控制策略进行仿真对比，在PSCAD/EMTDC中搭建如图6所示的仿真模型，仿真参数如表1所示。

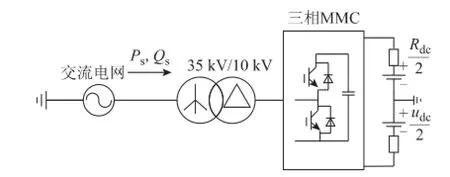
图6　MMC仿真模型Fig.6　Simulation model for MMC

表1　仿真模型参数Tab.1　The parameters of simulation model

5.1稳态性能

在电网电压对称及不对称两种情况下，对双矢量控制策略及本文提出的两种模型预测控制进行稳态性能测试。0.4 s时，A相电压发生50%的电压跌落，B、C相电压保持不变，电网电压不对称时采用抑制负序电流、保证三相电流平衡的控制目标。有功参考值为5 MW，无功参考值为-5 Mvar。3种控制策略的仿真结果如图7所示。

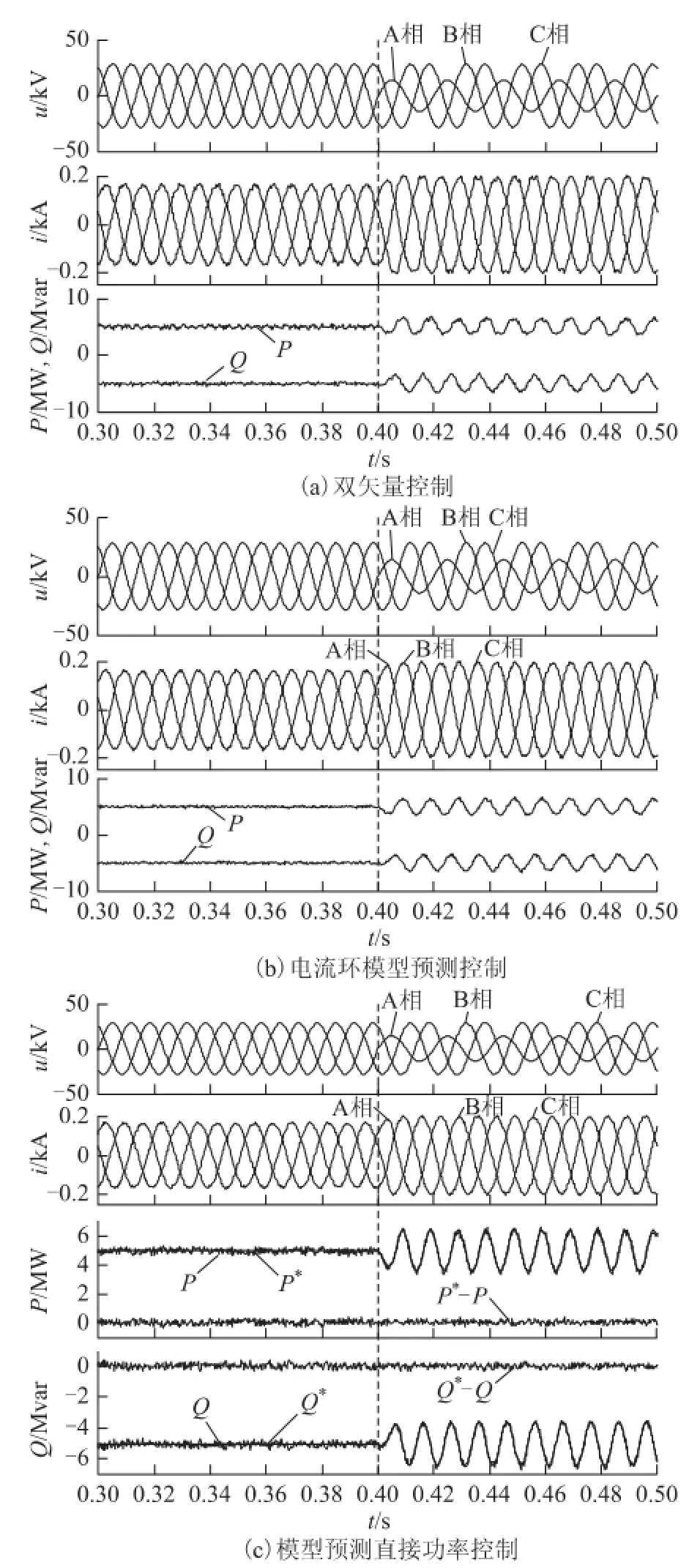
图7　3种控制策略稳态性能测试仿真结果Fig.7　Simulation results of steady-state performance test for three control strategy

由图7可看出，0.4 s之前电网电压对称，3种控制策略下的三相电流平衡；0.4 s时，A相电压发生跌落，三相电压变得不对称，由于采用抑制负序电流的控制目标，三相电流依然保持平衡。然而，由于有功和无功参考值始终保持不变，且负序电流为零，因此电网电压跌落后，三相电流较电网电压对称时有所增加。尽管电网电流中不存在负序电流，但负序电压与正序电流相互作用产生2倍频的波动分量PD、QD，使得有功和无功功率均出现波动。

电网电压不对称时相对于电网电压对称时电网电流的总谐波畸变率（Total Harmonic Distortion，THD）变化不大，因此，本文仅给出电网电压对称时电网电流的THD来比较3种控制策略的稳态性能，如表2所示。3种控制策略在电网电压不对称及对称时均可取得良好的控制效果，电网电流三相对称且波形质量较好。但相比之下，两种模型预测控制的稳态性能略优于双矢量控制。

表2　3种控制策略对应的电网电流THDTab.2　Grid current THD for three control strategy

由图7c可知，有功和无功参考值无论是直流量（0.4 s之前）还是含有2倍频波动分量（0.4 s之后），模型预测直接功率控制器均能使得实际功率准确跟踪参考功率。此外，模型预测直接功率控制虽然省略了电流内环，但并未降低电网电流的波形质量。

5.2动态性能

在A相电压发生50%电压跌落的故障条件下测试3种控制策略在有功或无功参考值发生跳变时的动态性能。

采用抑制有功波动的控制目标，在0.4 s时发生潮流反转，有功参考值由5 MW跳变至-5 MW，无功原始参考值Qconst始终为10 Mvar，仿真结果如图8所示。由图8可知，在3种控制策略下，有功功率的2倍频波动分量均得到有效抑制。由图8a可知，有功指令发生突变，采用双矢量控制策略时，有功功率需要约8 ms的时间跟踪上参考值；由图8b和图8c中的功率放大图可知，采用电流环模型预测控制和模型预测直接功率控制，有功功率在2 ms内即可跟踪上其参考值。双矢量控制策略需要对反馈电流进行正负序分解，由此带来的延时影响了控制系统的动态性能，使得双矢量控制与两种模型预测控制相比响应速度相对较慢。

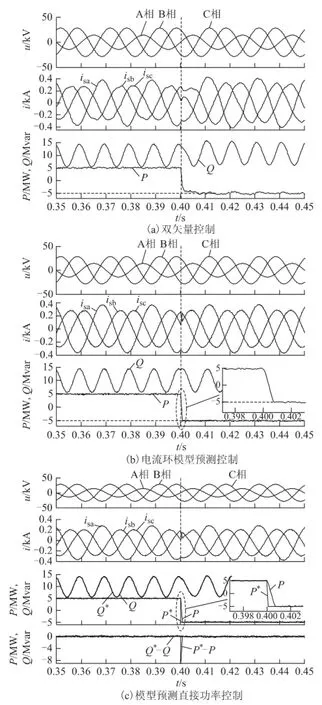
图8　抑制有功波动时动态性能测试仿真结果Fig.8　Simulation results of dynamic performance test with suppressing active power fluctuation

采用抑制无功波动的控制目标，有功原始参考值Pconst始终为10 MW，无功参考值在0.4 s由5 Mvar跳变至-5 Mvar，3种控制策略的仿真结果如图9所示。由图9可看出，在3种控制策略下，无功功率的2倍频波动分量均得到有效抑制。对比图9中3种控制策略的功率响应曲线可清晰地看出，无功参考值发生跳变后，电流环模型预测控制与模型预测直接功率控制的响应速度明显快于双矢量控制，进一步验证了两种模型预测控制在动态性能上的优势。

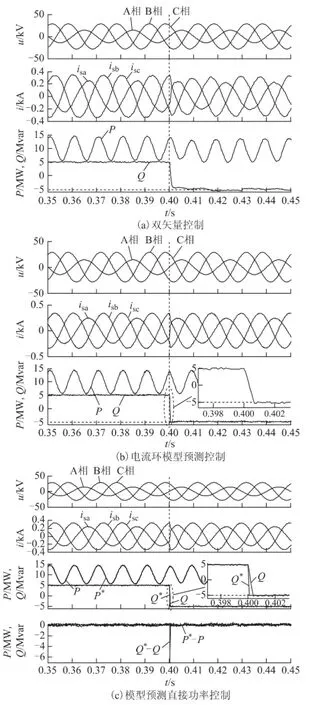
图9　抑制无功波动时动态性能测试仿真结果Fig.9　Simulation results of dynamic performance test with suppressing reactive power fluctuation

6　结论

本文在分析不对称电网电压下MMC数学模型及功率模型的基础上，提出MMC的电流环模型预测控制和模型预测直接功率控制。在PSCAD中搭建了MMC仿真模型，对3种控制策略进行了仿真对比分析，得出以下结论:

1）3种控制策略在电网电压对称及不对称情况下均能取得良好的稳态控制效果，稳态性能相差不大。

2）两种模型预测控制都在αβ坐标系下实现，不需要正负序电流的分离，因此其响应速度快于双矢量控制。两种模型预测控制的响应速度无明显差别。

3）3种控制策略在不对称电网电压下都可实现抑制负序电流、抑制有功波动和抑制无功波动3个控制目标。双矢量控制需要4个PI调节器对正负序电流的d、q轴分量分别控制，结构复杂。而两种模型预测控制不需要多个PI调节器，控制结构相对简单。

4）与电流环模型预测相比，模型预测直接功率控制省略了电流内环，可实现对功率的直接控制。虽然模型预测直接功率控制需要计算功率补偿量以得到新的参考功率，但与电流环模型预测控制的参考电流计算环节相比，计算公式相对简单。

［1］LesnicarA，MarquardtR.Aninnovativemodular multilevel converter topology suitable for a wide power range［C］//IEEEBolognaPowerTechConference，Bologna，Italy，2003:1-6.

［2］Bergna G，Garces A，Berne E，et al.A generalized power control approach in ABC Frame for modular multilevel converter HVDC links based on mathematical optimization［J］.IEEE Transactions on Power Delivery，2014，29（1）:386-394.

［3］Peralta J，Saad H，Dennetiere S，et al.Detailed and averaged models for a 401-level MMC-HVDC system［J］. IEEE Transactions on Power Delivery，2012，27（3）: 1501-1508.

［4］Moon J W，Kim C S，Park J W，et al.Circulating current control in MMC under the unbalanced voltage［J］.IEEE Transactions on Power Delivery，2013，28（3）:1952-1959.

［5］Song H S，Nam K.Dual current control scheme for PWM converter under unbalanced input voltage conditions［J］.IEEE Transactions on Industrial Electronics，1999，46（5）:953-959.

［6］魏晓云，孙辉，魏晓光，等.改善电能质量的电压源换流器高压直流输电不平衡控制策略［J］.中国电机工程学报，2011，31（9）:8-14. Wei Xiaoyun，Sun Hui，Wei Xiaoguang，et al.Strategy about power quality improvement for VSC-HVDC under unbalanced AC grid conditions［J］.Proceedings of the CSEE，2011，31（9）:8-14.

［7］Hu J，He Y.Modeling and control of grid-connected voltage-sourced converters under generalized unbalanced operation conditions［J］.IEEE Transactions on Energy Conversion，2008，23（3）:903-913.

［8］张建坡，赵成勇，敬华兵，等.比例谐振控制器在MMC-HVDC控制中的仿真研究［J］.中国电机工程学报，2013，33（21）:53-62. Zhang Jianpo，Zhao Chengyong，Jing Huabing，et al. Simulating research of proportional resonant controllers in MMC-HVDC［J］.Proceedings of the CSEE，2013，33（21）:53-62.

［9］马宏伟，李永东，郑泽东，等.电流环模型预测控制在PWM整流器中的应用［J］.电工技术学报，2014，29（8）:136-141. Ma Hongwei，Li Yongdong，Zheng Zedong，et al. PWM rectifier using a model predictive control method in the current loop［J］.Transactions of China Electrotechnical Society，2014，29（8）:136-141.

［10］ 郑泽东，王奎，李永东，等.采用模型预测控制的交流电机电流控制器［J］.电工技术学报，2013，28（11）:118-123. ZhengZedong，WangKui，LiYongdong，etal. Current controller for AC motors using model predictive control［J］.TransactionsofChinaElectrotechnical Society，2013，28（11）:118-123.

［11］Mohamed I S，Zaid S A，Abu-Elyazeed M F，et al. Model predictive control of an inverter with output LC filter for UPS applications［J］.IEEE Transactions on Industrial Electronics，2009，56（6）:1875-1883.

［12］Vargas R，Ammann U，Rodriguez J.Predictive approach to increase efficiency and reduce switching losses on matrixconverters［J］.IEEETransactionsonPower Electronics，2009，24（4）:894-902.

［13］ 章玮，王宏胜，任远，等.不对称电网电压条件下三相并网型逆变器的控制［J］.电工技术学报，2010，25（12）:103-110. Zhang Wei，WangHongsheng，RenYuan，etal. Investigation on control of three-phase grid-connected inverters under unbalanced grid voltage conditions［J］. Transactions of China Electrotechnical Society，2010，25（12）:103-110.

［14］ 赵新，金新民，周飞，等.基于比例积分-降阶谐振调节器的并网逆变器不平衡控制［J］.中国电机工程学报，2013，33（19）:84-92. Zhao Xin，Jin Xinmin，Zhou Fei，et al.Unbalanced control of grid-connected inverters based on proportion integralandreducedorderresonantcontrollers［J］. Proceedings of the CSEE，2013，33（19）:84-92.

［15］孔明，汤广福，贺之渊，等.不对称交流电网下MMC-HVDC输电系统的控制策略［J］.中国电机工程学报，2013，33（28）:41-49. Kong Ming，Tang Guangfu，He Zhiyuan，et al.A control strategy for modular multilevel converter based HVDC of unbalanced AC systems［J］.Proceedings of the CSEE，2013，33（28）:41-49.

［16］Akagi H，Kanazama Y，Nanae A.Instantaneous reactive power compensators comprising switching devices without energy storage components［J］.IEEE Transactions on Industrial Electronics，1984，20（3）:625-630.

［17］Abad G，Rodriguez M A，Iwanski G，et al.Direct powercontrolofdoubly-fed-induction-generator-based wind turbines under unbalanced grid voltage［J］.IEEE Transactions on Power Electronics，2010，25（2）: 442-452.

［18］Shang L，Sun D，Hu J.Sliding-mode-based direct power control of grid-connected voltage-sourced inverters under unbalanced network conditions［J］.IET Power Electronics，2011，4（5）:570-579.

［19］Shang L，Hu J.Sliding-mode-based direct power control of grid-connected wind-turbine-driven doubly fed induction generators under unbalanced grid voltage conditions［J］. IEEE Transactions on Energy Conversion，2012，27（2）: 362-373.

［20］Hu J，Zhu J，Dorrell D G.Model-predictive direct power control of doubly-fed induction generators under unbalancedgridvoltageconditionsinwindenergy applications［J］.IETRenewablePowerGeneration，2014，8（6）:687-695.

The Applications of the Model Predictive Control for MMC-HVDC

Liang Yingyu1Zhang Tao2Liu Jianzheng3Yang Qixun1Mei Hongming2Liu Shu2
（1.State Key Laboratory for Alternate Electrical Power System with Renewable Energy Sources North China Electric Power UniversityBeijing102206China 2.Beijing Sifang Automation Co.Ltd.Beijing100085China 3.State Key Lab of Control and Simulation of Power Systems and Generation Equipments Tsinghua UniversityBeijing100084China）

Aiming at eliminating the existing shortcomings of the traditional unbalanced control strategy for high voltage direct current transmission based on modular multilevel converter（MMC-HVDC）under asymmetry ac system，this paper proposes two improved unbalanced control methods，i.e.the current loop model predictive control and the model predictive direct power control.The two proposed methods achieve ac-side current control and ac-side active power and reactive power control of MMC，respectively.The control principle and the design process of the two methods are described in detail.In addition，the traditional dual vector control strategy is compared with them in respect of the control structure complexity，the steady-state performance，and the dynamic performance.In order to achieve three control targets under the asymmetric ac system，i.e.suppressing negative current，eliminating active power ripples，and removing reactive power ripples，the model predictive direct power control is combined with the power compensation strategy.To validate the correctness and the effectiveness of the two proposed control methods，a five level MMC-HVDC model is set up in PSCAD/EMTDC.

Modular multilevel converter，model predictive control，direct power control，double vector control，asymmetry grid voltage

TM721.1

2015-01-23改稿日期 2015-11-10

梁营玉男，1989年生，博士研究生，研究方向为HVDC和柔性交流输配电技术。

E-mail:liangyingyu2013@163.com（通信作者）

张涛男，1971年生，教授级高工，研究方向为电力系统保护与控制、电力电子在电力系统中的应用、新能源并网等。

E-mail:zhangtao@sf-auto.com