基于磁饱和效应的表贴式永磁同步电机初始位置检测方法

田　兵　安群涛　孙东阳　孙　力　赵　克

（哈尔滨工业大学电气工程系　哈尔滨　150001）

基于磁饱和效应的表贴式永磁同步电机初始位置检测方法

田兵安群涛孙东阳孙力赵克

（哈尔滨工业大学电气工程系哈尔滨150001）

根据表贴式永磁同步电机磁饱和效应模型检测转子初始位置，并通过有限元分析验证了其有效性；在位置检测算法上采用旋转电压注入法，通过高通与谐振滤波器显著放大微弱的高频电流响应，并高效衰减直流成分；结合改进的解调算法，准确提取出负序直流分量和铁心饱和度评价函数；转子位置检测结果由锁相环估算的转子方向结合基于饱和度评价函数的磁极极性判定方法来确定。通过Matlab/Simulink搭建了表贴式永磁同步电机零速下磁饱和仿真平台，验证了该文所提算法的有效性，同时硬件平台实验进一步验证了该方法具有简单可靠、准确度较高等特点。

表贴式永磁同步电机初始位置检测磁饱和效应高通与谐振滤波器锁相环

0　引言

永磁同步电机具有功率密度高、结构简单以及调速性能好等优点，在工业领域获得广泛应用［1］。通常永磁同步电机转子轴需要安装机械位置传感器，它大大降低了调速系统的可靠性，因此无位置传感器技术成为国内外的研究热点。永磁同步电机无位置传感器技术在低速甚至零速阶段，实现起来较为困难。通常低速无位置传感器转子位置估算准确度依赖于永磁同步电机凸极率（交直轴自感之比，即Lqq/Ldd，且Lqq/ Ldd=1时高频电流响应不能被磁极位置调制）。由于表贴式永磁同步电机（后文统一简称表贴式电机）铁心中交直轴磁路较为均衡，自身的凸极率较低（表现为Lqq/Ldd≈1），因此低速下较难实现转子位置估算［2］。

表贴式电机初始位置检测可分为两类:一种是利用其磁路固有饱和特性（铁心工作在膝点，凸极率较低）［3-6］，采用类似于内置式永磁同步电机初始位置估算方法；二是通过注入定子励磁电流，制造磁路饱合，增加凸极率，改善位置检测准确度［7-9］。文献［3］通过在零速下注入高频旋转电压矢量，采用简单的解调方法从高频响应电流中提取转子位置信息来估算转子位置。这种方法需要注入较大的旋转电压矢量（可提高信噪比），转子轻载或空载较易引起电机振动。文献［4］提出通过电机定子槽特殊设计，采用脉振电压注入法，可使表贴式电机实现全速范围内转子位置检测。文献［5］通过在定子侧施加低频旋转电压矢量，使电机（来回）脉动。由于脉动转速和转子位置有关，脉动转速将产生反电动势，并作用于电机，其位置信息便可由响应电流通过傅里叶分析提取出来。这种方法对DSP性能要求较高。文献［6］根据表贴式电机定子空载时工作于膝点，并注入高频脉振电压，通过一种新颖的位置观测器，提取出转子位置信息。文献［7］通过在定子侧注入一组方波电压矢量（可改变铁心饱和度，即改变凸极率），测量并比较相电流响应幅值确定转子位置信息。文献［8］通过有限元分析建立了无刷直流电机的模型，在某相绕组中注入电压矢量（可改变凸极率），然后测量并比较其他两相相电流响应来确定转子位置，这种方法估算准确度是60°电角度。文献［9］通过注入较大的高频方波电压（可改变凸极率），测量并比较响应电流峰值大小确定转子位置；由于电流响应呈三角形，当不采用解调算法时，确定峰值较为困难。除此之外，当采用改变铁心饱和度的方法时，如果注入的定子励磁电流/电压不在永磁体轴线上时，较易引起轻载或空载时电机转动。

另外，对于表贴式电机而言，当铁心磁路饱和时（意味着凸极率增加），会使交直轴发生磁耦合（存在交直轴互感，即Ldq和Lqd），从而引入一个磁耦合角，因此基于人为营造磁饱和的方法还会增加转子位置检测的难度和准确性［10-15］。文献［12］建立了一个较全面的永磁同步电机非线性模型解释这种磁饱和以及磁耦合现象，且模型有效性和准确性得到了实验验证。

谐振控制器在有源电力滤波、单相光伏逆变器以及电机驱动等场合应用广泛，这是由于谐振控制器对谐振点（包括正序和负序）提供无穷大增益，而对远离谐振点的信号亦可实现显著衰减，从而对谐振频率点实现闭环无静差调节。但谐振调节器调节速度较慢，通常为了改善谐振控制器频率响应带宽，一般采用比例谐振控制器［16，17］。本文结合谐振控制器选频特性和高通滤波器低频抑制特性，将之应用于信号提取场合。

考虑到表贴式电机初始位置检测存在的上述问题，本文根据文献［12］中表贴式电机的磁饱和数学模型以及电机铁心固有磁饱和特性（工作于膝点，且此时磁耦合角为零），采用高频旋转电压注入法［18，19］，通过谐振滤波器和新颖的解调算法来获得转子方向信息和当前铁心饱和度信息。对于转子方向估算（本文中转子方向特指永磁体轴线方向，区别于转子位置），可通过角度观测器准确获得；对于永磁体N/S极的判定，则在估算的转子方向基础上，只需注入一个直流电压矢量，比较注入前后铁心饱和度即可。本文通过有限元分析（Finite Element Analysis，FEA），首先验证了表贴式电机磁饱和模型的有效性；通过Matlab/ Simulink搭建了表贴式电机零速下磁饱和仿真平台，并验证了转子方向估算算法和磁极极性判断算法的正确性；最后硬件平台实验则更进一步验证了本文转子初始位置检测方法具有实施简单、准确度较高等优点。

1　表贴式永磁同步电机磁饱和模型

1.1dq坐标系下表贴式电机数学模型

考虑到磁饱和以及磁耦合现象，表贴式永磁同步电机在dq坐标系下的数学模型为

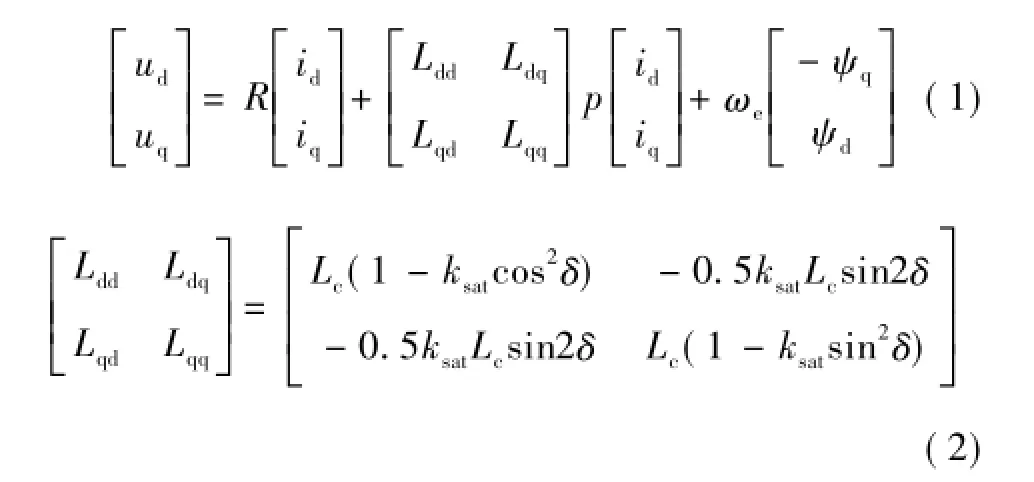
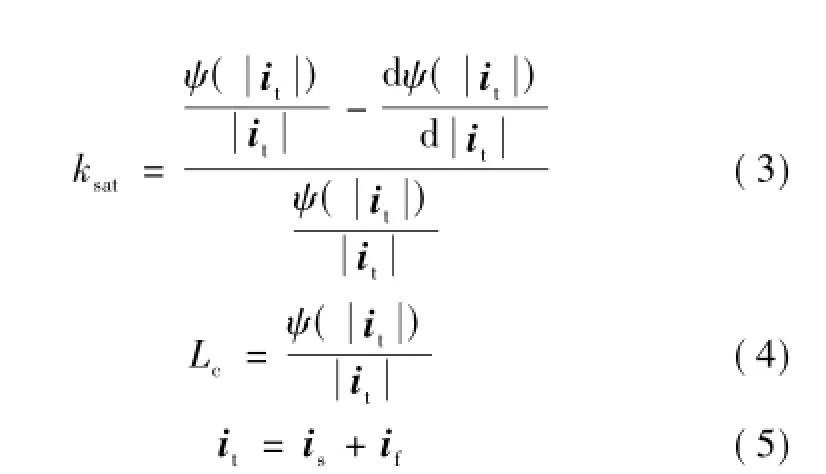
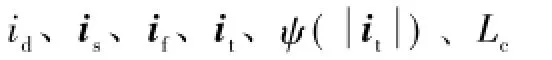
图1　铁心励磁电流与磁路特性Fig.1　Flux linkage and excitation current inside the iron core

通常由于电机定子空载时铁心工作于膝点，其磁路固有的饱和度引起ksat＞0、δ=0，从而使Lqq和Ldd出现微小偏差，利用此微弱交直轴自感偏差可估算转子位置。

1.2αβ坐标系下表贴式电机高频数学模型

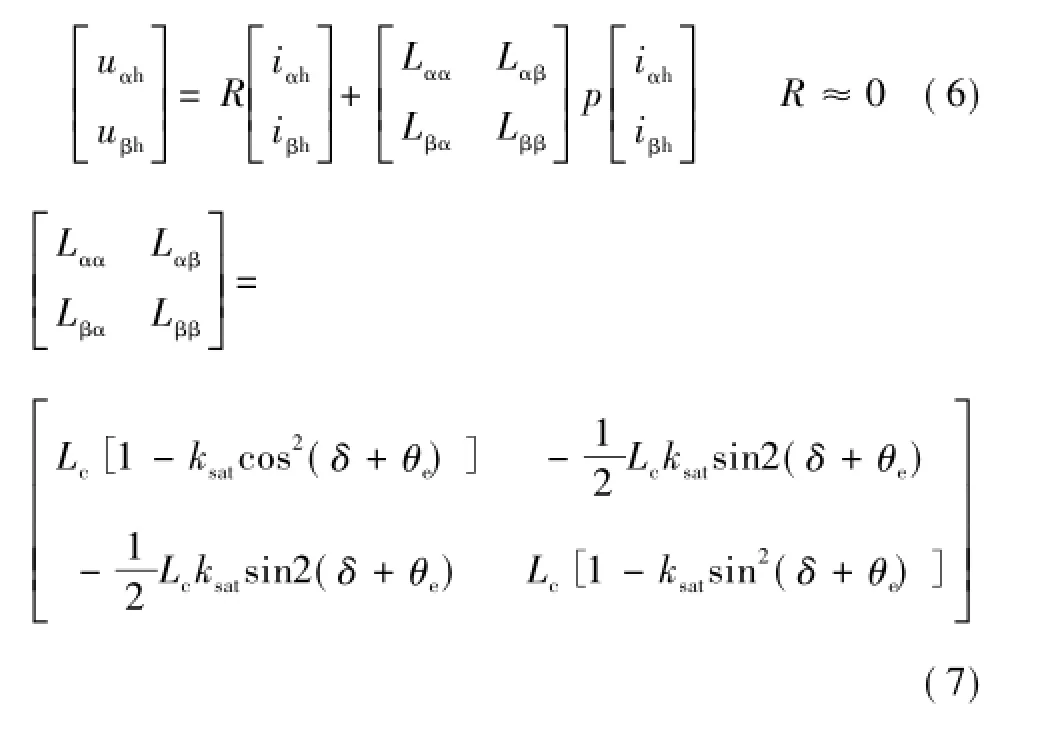
当采用高频旋转注入法时，表贴式电机在dq坐标系下的磁饱和模型不能反映转子位置信息，因此将它转换到αβ坐标系下，并忽略定子电阻（远小于高频阻抗），有式中，uαh和uβh分别为输入的高频旋转电压，V，其表达式如式（8）所示；iαh和iβh分别为高频响应电流，A；Lαα、Lββ、Lαβ和Lβα分别为αβ轴系上自感和互感，H；θe为转子位置，rad；p为微分算子。

式中，vim为高频旋转电压幅值；ωih为高频旋转电压角速度。

解得高频电流响应，并采用矢量表示为

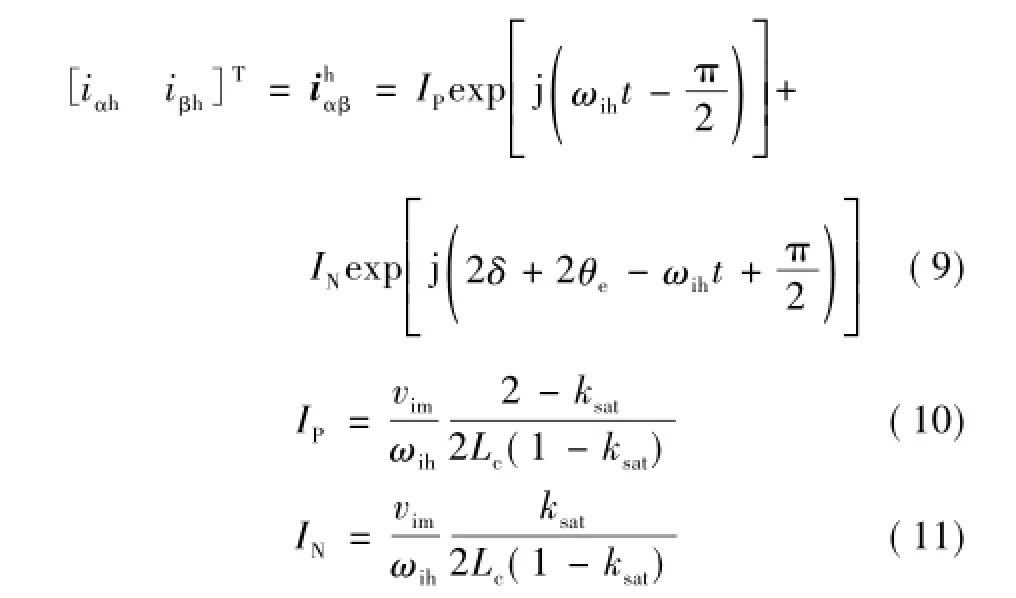
1.3有限元分析

通过Maxwell/Ansoft软件对一台4对极、齿槽数为48的表贴式电机进行了有限元分析，并计算了交直轴电感动态变化情况。

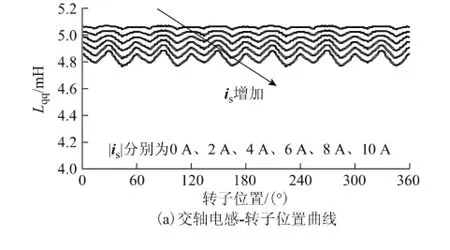
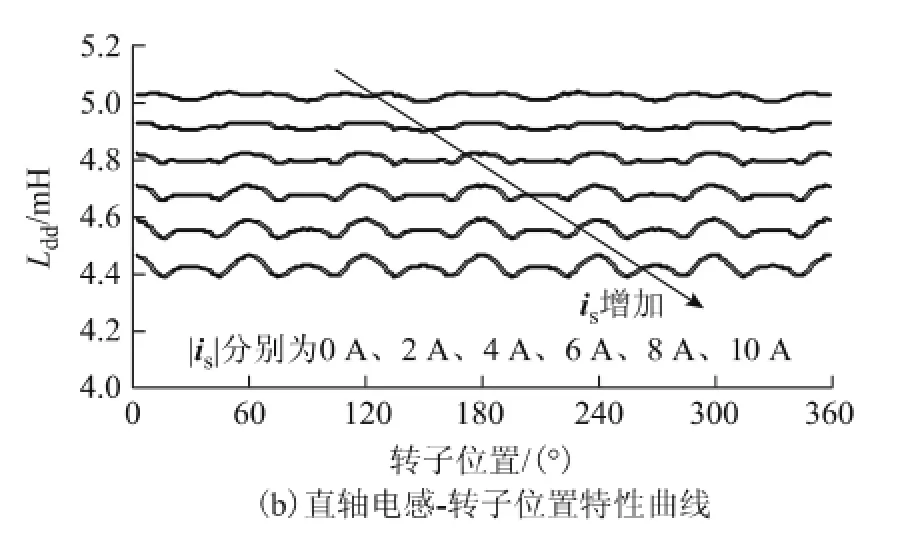
图2　交直轴自感有限元分析计算Fig.2　Lqqand Lddcalculation via FEA method

图2中交直轴电感出现波动，是由电机齿槽效应引起，然而电机静止状态下，其交直轴电感是明确的，并不妨碍本文初始位置检测。

2　谐振滤波器和相应解调算法

2.1谐振滤波器的引入

表贴式电机在空载状态下，铁心凸极率较低，当采用高频旋转电压注入法时，通常需要提高高频旋转电压幅值来获取较大的响应电流，这是因为表贴式电机凸极率不明显，增大高频响应电流可提高信噪比（高频属于有用信号），弥补由模拟采样通道引入的低频成分和开关频率谐波成分。但这样会引起电机振动，不利于初始位置检测。本文注入较低幅值的高频旋转电压，采用高通与谐振滤波器，可高效地提取转子位置信息。高通与谐振滤波器传递函数如式（12）所示，其伯德图如图3所示［16，17］。

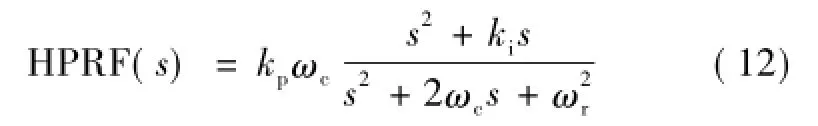
式中，HPRF为高通与谐振滤波器（High Pass and Resonance Filter，HPRF）；ωr为谐振频率，rad/s；ωc为带宽，rad/s；kp为比例系数，ki为积分系数。本文选取谐振点在高频电流响应频率处（即ωr=ωih）。

图3为高通与谐振滤波器伯德图，具体参数为: ωr=2π×500，ωc=5，kp=0.1，ki=100。由图可知，该谐振滤波器在谐振点处增益为34 dB，而在低频段增益为-111 dB，在开关频率处增益约为-5.9 dB。由此可见，滤波器可实现对特定频率点（包括正序和负序）增益的显著提升，同时不损失较强的低频抑制能力，可微弱衰减或不衰减开关频率谐波（开关频率处谐波对下文的解调算法影响不大，且较易滤除）。除此之外，滤波器在谐振点会出现90°相移（相位超前90°），其固定相移亦可通过新颖解调方法予以补偿。

通常在提取高频电流响应时，传统做法是采用二阶带通滤波器［3，4，6］。二阶带通滤波器理论上可对低频段和开关频率处有较强的抑制性能，对谐振点实现幅值无衰减和相位无滞后/超前滤波。然而在实际数字化过程中，二阶带通滤波器对有用的高频信号滤波时，相位会存在一定情况的滞后，且二阶带通滤波器带宽越窄，相位滞后越严重。虽然这种不固定的相移亦可采取相应方法补偿，但增加了数字滤波器的复杂性和弱化了其通用性。

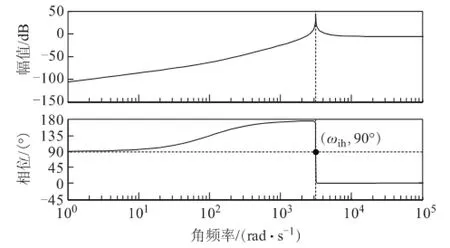
图3　高通与谐振滤波器伯德图Fig.3　Bode plot for high pass and resonance filter

针对这种情况，同为二阶滤波器的谐振滤波器更适合提取并放大高频电流响应（包括正负序分量）。

2.2转子方向信息提取

原始响应电流经过滤波器滤波，并忽略开关频率谐波电流，便可得到移相90°的高频响应电流为

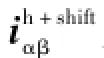
经过如下调制即可提取出负序分量

2.3铁心饱和度评价函数

当采用高频旋转电压注入法估算转子初始位置时，通常只提取负序分量幅值来估算转子方向，本文采用上文类似的方法提取出正序分量幅值，并用于估算磁极极性。

正序分量可通过如下调制方法提取

为了便于磁极极性判断，本文引入铁心饱和度评价函数为

式中，fsat为铁心饱和度评价函数。由铁心磁路特性可知，铁心越饱和，凸极率越高，负序分量占的比重也就越大，而fsat完全可表征铁心这一特性。

3　转子位置检测方法

由于表贴式电机空载时，磁耦合角δ=0，ksat＞0。因此转子方向估算可通过如图4所示的锁相环（Phase-Locked Loop，PLL）完成。

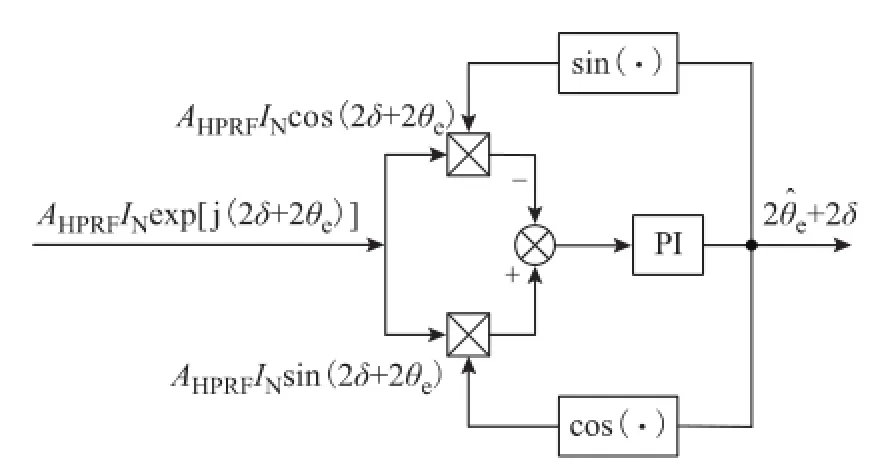
图4　锁相环观测转子方向Fig.4　Rotor direction estimation with PLL

在估算出转子方向后，还需要结合磁极极性，确定转子方向。对于磁极极性，有效的方法是在获得转子方向的基础上，采用正反两个方向直流电压矢量，测量并比较瞬态定子励磁电流响应［6］（此时铁心饱和度不同，引起交直轴自感变化，而电感变化仅体现在定子直流励磁电流瞬态响应过程，其稳态值由定子相电阻决定），这种测量电流响应时间的方法实现起来，需要严格注意注入直流电压和测量电流响应之间严格的时序关系以及噪声信号引入的干扰。

4　仿真结果

为了验证初始位置检测算法的有效性，搭建了Matlab/Simulink仿真平台，如图5所示，其中表贴式电机零速下磁饱和模型采用S-function编写。图5中，开关Sw拨至“0”，表示没有注入直流电压矢量；Sw拨至“1”，表示注入幅值为C的直流电压矢量，此时进行磁极极性判断。其中仿真参数设置见表1。

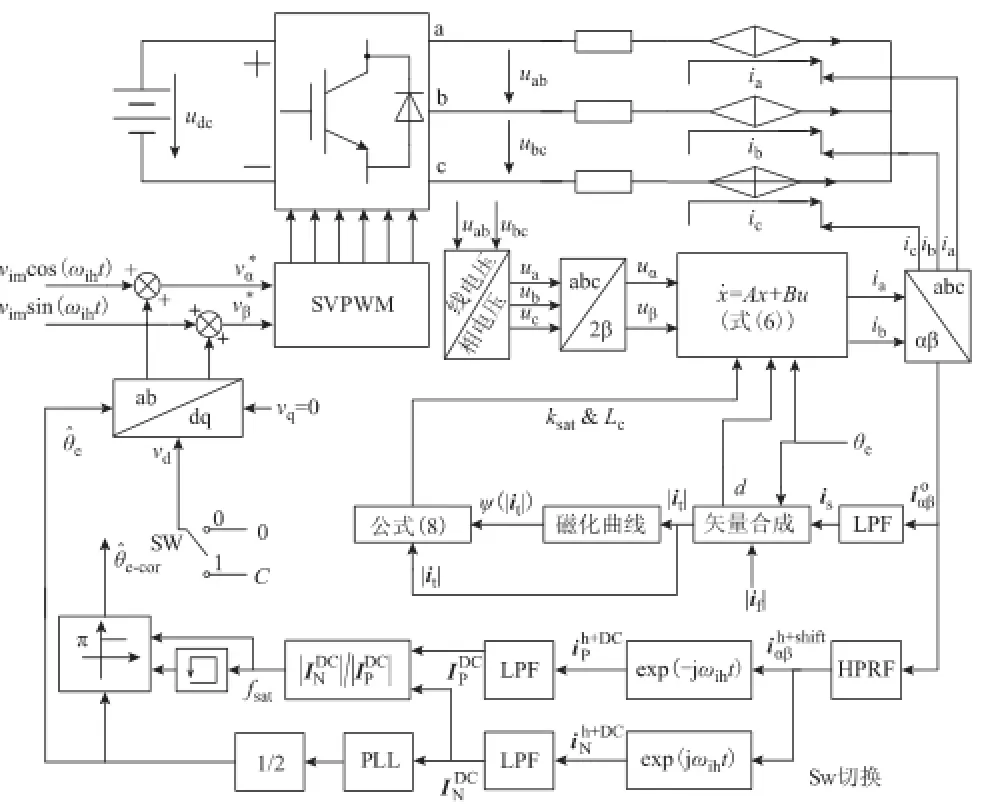
图5　仿真平台Fig.5　Simulation platform

表1　仿真平台参数设置Tab.1　Preference setting for simulation platform

图6为α轴高频电流响应经高通与谐振滤波后幅频和相频变化情况（谐振点增益显著，且相位超前90°）。图7为经滤波后的αβ坐标系下高频电流响应，可看出，α轴和β轴高频电流响应的幅值存在差异，也就是出现了负序分量，这是由于高频电流响应被转子凸极效应所调制，其蕴含的负序分量对于转子位置检测是必须的。采用该谐振滤波器可显著提升谐振频率处高频电流响应的幅值，而对低频的抑制能力毫不衰弱（实际驱动系统会由于模拟采样通道零点漂移引入直流分量，另外本文在磁极极性判别中会引入直流定子电流改变铁心饱和度）。

图6　高通与谐振滤波器滤波效果（仿真）Fig.6　Simulation results for the performance of high pass and resonance filter

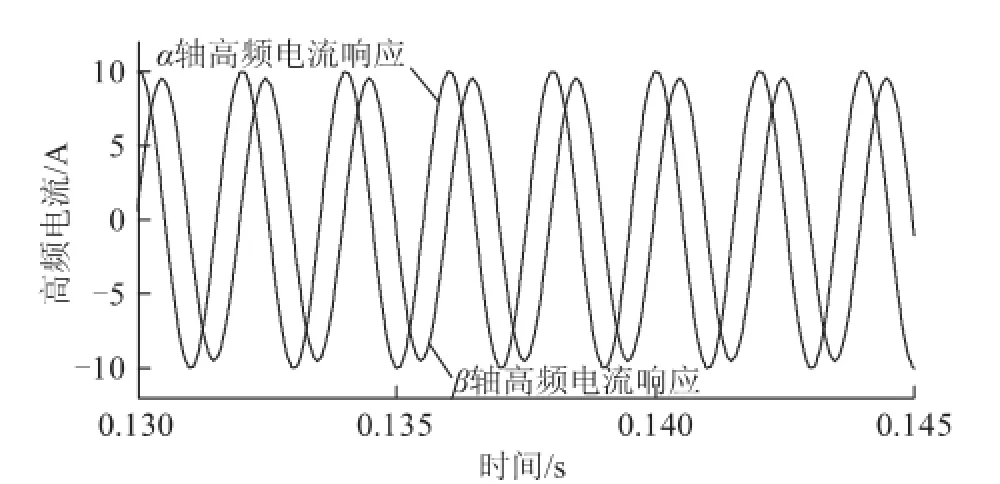
图7　高频电流响应被磁饱和凸极调制（仿真）Fig.7　Simulation results for HF current responses modulated by magnetic saliency

图8为采用本文解调算法提取出图7所示的负序分量，该负序直流分量可通过如图9所示的PLL锁相环准确估算出转子方向。

图8　提取的负序直流分量（仿真）Fig.8　Simulation results for extracting negative-sequence DC components

图9　实际位置和PLL估算转子位置（仿真）Fig.9　Simulation results for the estimated rotor position by PLL and the actual one

在估算出转子方向之后，还要结合磁极极性判断确定最终估算的转子位置。图10为在估算转子方向的基础上，注入一个直流电压矢量，由直流电压矢量产生的定子直流励磁电流呈增磁作用（由饱和度评价函数fsat表征），因此转子方向即为磁极方向，也是转子位置。由图9所示，此时估算误差为10.5°，它完全能满足表贴式电机重载起动场合。

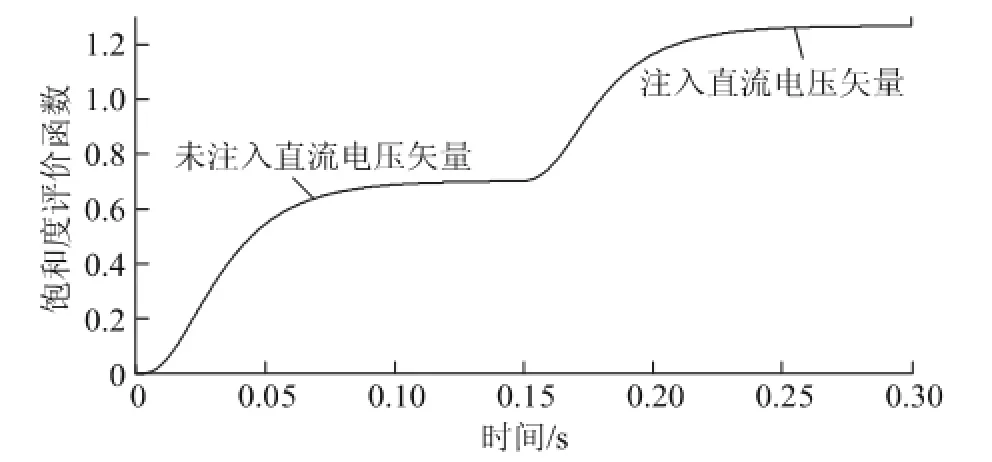
图10　判断磁极极性（仿真）Fig.10　Simulation results for identifying magnetic polarity

5　实验结果及分析

搭建了表贴式电机驱动系统平台，采用TMS320F2812系列DSC，其中IGBT工作频率为10 kHz，采样频率为15 kHz；谐振滤波器数字离散化频率为15 kHz，其余算法离散化频率均为10 kHz。电机参数中永磁体磁链ψf、定子电阻R以及控制参数与表1相同，其中本文所采用电机的交直轴自感名义值为Ldd= Lqq=4.8 mH。

图11为α轴高频电流响应经高通与谐振滤波后出现幅频和相频情况。图12为谐振滤波后αβ坐标系下高频电流响应，由图可知，高频电流响应中包含负序分量，由于表贴式电机凸极效应较弱，因此α轴和β轴高频电流响应在幅值上的差异没有内置式电机强烈；由于采用谐振滤波器，其微弱的负序分量依然能够被谐振滤波器检测出，并显著放大，用于转子位置估算。

图11　高通与谐振滤波器滤波效果（实验）Fig.11　Experimental results for the pertomance of high pass and resonance filter

图12　高频电流响应被磁饱和凸极调制（实验）Fig.12　Experimental results for HF current responses modulated by magnetic saliency

高频电流响应经式（15）所示方法解调运算，可提取出负序二倍频分量和负序直流分量。如图13所示的负序二倍频（2×500 Hz）可通过惯性滤波器滤除，得到单纯的负序直流分量，用于锁相环转子方向估算。同时，经式（17）解调运算，可得到正序二倍频分量和正序直流分量。如图14所示的正序二倍频分量（2× 500 Hz）亦可通过惯性滤波器滤除，正序直流分量和负序直流分量可合成饱和度评价函数fsat，用于判断磁极极性。

图13　负序二倍频分量（实验）Fig.13　Experimental results for extracting negative-sequence second-harmonic components

如图15所示，通过上述步骤提取出的负序直流分量，可估算出转子方向，结合如图16所示的磁极极性判断，可确定最终估算的转子位置为73.8°。如图17所示，本文初始位置检测平均误差（绝对值）为13.1°。该误差产生的原因有:忽略定子电阻和IGBT死区时间，模数转换器精度较低（TMS320F2812片内ADC），定点DSP模拟浮点数运算精度以及表贴式电机定子凸极率较低（主要因素）。

图14　正序二倍频分量（实验）Fig.14　Experimental results for extracting positive-sequence second-harmonic components

图15　实际和PLL估算转子位置（实验）Fig.15　Experimental results for actual and estimated rotor positions by PLL

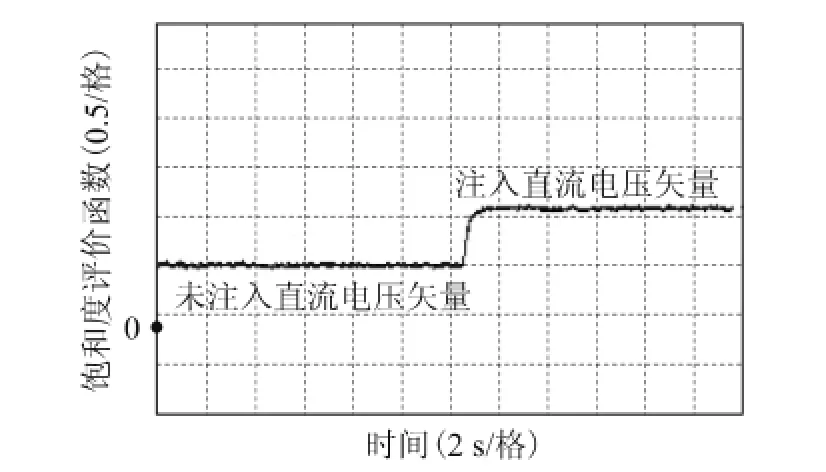
图16　磁极极性判断（实验）Fig.16　Experimental results for identifying magnetic polarity

图17　转子位子检测误差分布Fig.17　Experimental results for estimation error distribution versus rotor position

采用本文初始位置估算方法得到的角度进行电机起动实验。

由于电磁转矩表达式为［12］

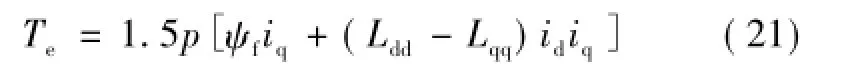
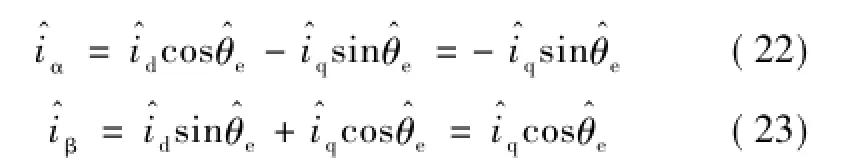
带入式（21）可得

对于表贴式永磁同步电机而言，由于交直轴电感差异较小，有（Ldd-Lqq）sin2Δθ≈0，电磁转矩可描述为

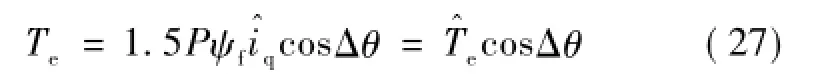
图18为起动对比实验，精确的位置信号由光电编码器给出。图18a为在满载情况（满载转矩为3 N·m，负载形式为磁粉制动器）且无位置估算偏差下起动永磁同步电机，电机正常起动；图18b为存在位置估算偏差下（此时，控制时初始角度等于真实转子角度减去角度位置偏差17°）起动电机，电机不能起动。在缓慢减载（磁粉制动器缓慢减载为92%）后，定子通以相同大小电流，永磁同步电机方能起动。图 18c和图18d为减载荷情况下起动电机时，电机转子位置、相电流和转速变化曲线。

然而，由于永磁同步电机存在一些非线性因素（如定位力矩波动）以及粘滞摩擦转矩等因素影响，实际起动效果并未达到95.6%的满载起动效果，但它足可以用于92%的满载工况。

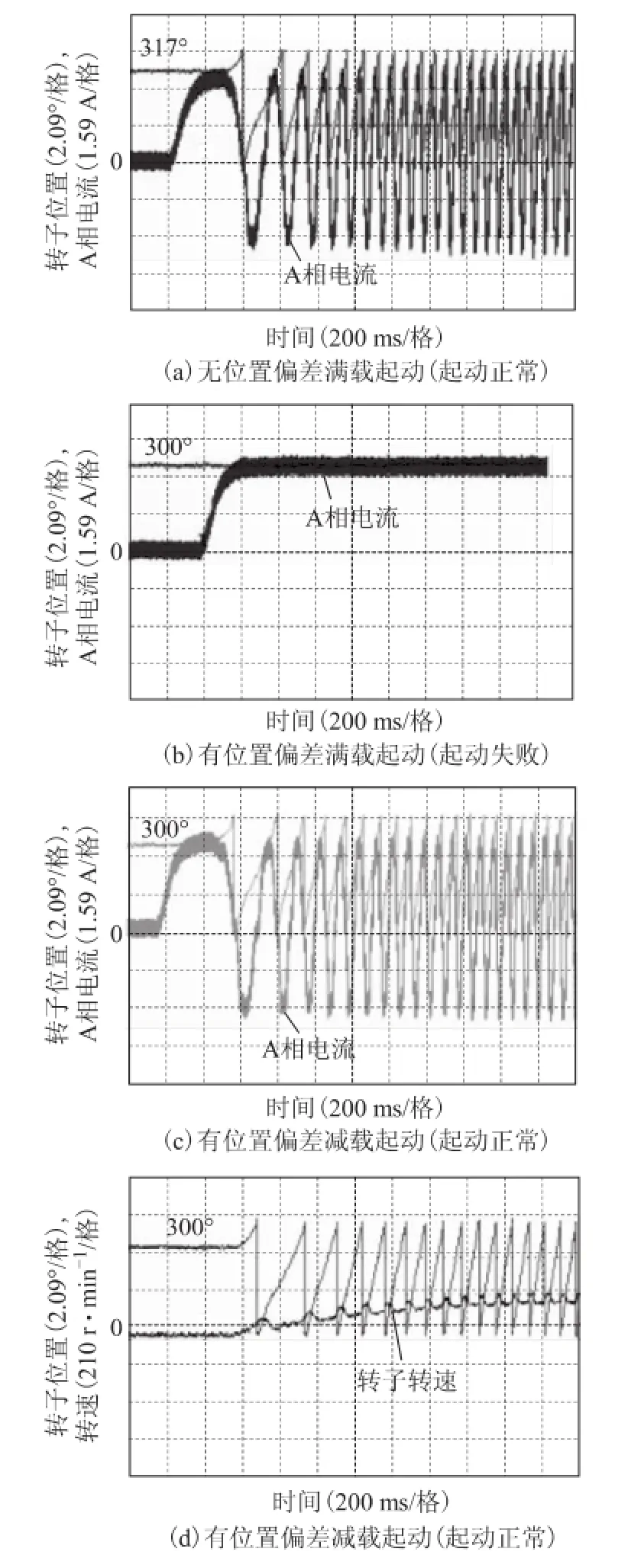
图18　起动电机实验对比Fig.18　Contrast experiments for starting a motor

通常，永磁同步电机低速无位置传感器技术采用脉振电压注入法（或最近兴起的高频方波注入法），即仅在估算d轴上注入高频正弦电压信号（高频方波信号），从估算q轴提取高频响应电流，并通过解调算法，得到转子位置误差信号，然后通过位置观测器（通常为PI调节器+积分器的结构），得到估算转子位置，此估算的转子位置实时参与调速系统闭环控制，进一步促使位置观测器收敛至真实转子位置。但这种方法稳定性较高频旋转注入法弱，尤其对于表贴式永磁同步电机而言，在交直轴电感差异较小的情况下，控制难度较大，易引起位置观测器收敛失败。因此，结合鲁棒性强的表贴式永磁同步电机低速无位置传感器技术是本文以后的研究方向。

对于初始位置观测和无位置控制策略的结合，就现阶段而言，本文初始位置估算方法可替代开关霍尔传感器（位置分辨误差固定为±30°），用于92%满载起动场合，也可用于基于开关霍尔位置传感器的高性能调速系统控制起动过程（通过估算转速并积分，弥补开关霍尔传感器±30°之间的分辨空挡）以及随表贴式永磁同步电机低速无位置传感器技术的改善，本文算法保证位置观测器正常/加速收敛。除此之外，本文算法适用于内置式永磁同步电机初始位置估算。

6　结论

本文根据表贴式永磁同步电机磁饱和模型，采用高频旋转电压注入法，高通与谐振滤波器和改进的解调算法，从原始高频电流响应中准确提取出转子方向信息和铁心饱和度评价函数，其中转子方向可通过锁相环准确估算，结合注入的直流电压矢量（改变铁心饱和度，确定磁极极性）可估算出最终转子位置。该初始位置检测算法采用两个高通与谐振滤波器及4个惯性滤波器，具有简单可靠等优点；其中高通与谐振滤波器结合新型解调算法可高效提取出被转子凸极所调制的负序分量，而注入微弱的旋转电压可有效避免电机振动和磁耦合角引入等问题。最后，仿真和实验验证了本文算法的有效性。本文初始位置检测方法平均误差为13.1°，最大误差为17°，误差产生的主要原因在于本文所采用的表贴式永磁同步电机凸极率较低，但它可满足电机92%满载起动场合。

［1］邱鑫，黄文新，卜飞飞.内置式永磁同步电机宽转速范围无位置传感器直接转矩控制［J］.电工技术学报，2014，29（9）:92-99. Qiu Xin，Huang Wenxin，Bu Feifei.Sensorless direct torque control of interior permanent magnet synchronous machines over wide speed range［J］.Transactions of China Electrotechnical Society，2014，29（9）:92-99.

［2］Seilmeier M，Piepenbreier B.Modeling of PMSM with multiple saliencies using a stator-oriented magnetic circuit approach［C］//Electric Machines&Drives Conference（IEMDC），Niagara Falls，Canada，2011.

［3］廖勇，沈朗，姚骏，等.改进的面贴式永磁同步电机转子初始位置检测［J］.电机与控制学报，2009，13（2）:203-207. Liao Yong，Shen Lang，Yao Jun，et al.initial rotor position detection for surface mounted PMSM Based on high frequency signal injection［J］.Electric Machines and Control，2009，13（2）:203-207.

［4］胡家兵，贺益康，年珩，等.基于磁饱和凸极效应的面贴式PMSM零速下无传感器技术［J］.中国电机工程学报，2006，26（10）:152-157. Hu Jiabing，He Yikang，Nian Heng，et al.The zerospeed sensorless control for surface mounted PMSM based on the magnetic-saturation saliency-effect［J］.Proceeding of CSEE，2006，26（10）:152-157.

［5］李毅拓，陆海峰，瞿文龙，等.一种新颖的永磁同步电机转子初始位置检测方法［J］.中国电机工程学报，2013，33（3）:75-82，13. Li Yituo，Lu Haifeng，Qu Wenglong，et al.A novel initial rotor position pstimation method for permanent magnet synchronous motors［J］.Proceeding of CSEE，2013，33（3）:75-82，13.

［6］刘颖，周波，李帅，等.转子磁钢表贴式永磁同步电机转子初始位置检测［J］.中国电机工程学报，2011，31（18）:48-54. Liu Ying，Zhou Bo，Li Shuai，et al.Initial rotor position detection of surface mounted permanent magnet synchronous motor［J］.Proceeding of CSEE，2011，31（18）:48-54.

［7］Nakashima S，Inagaki Y，Miki I.Sensorless initial rotor position estimation of surface permanent-magnet synchronous motor［J］.IEEE Transactions on Industry Applications，2000，36（6）:1598-1603.

［8］Zhao W，Niu S，Ho S L，et al.A position detection strategy for sensorless surface mounted permanent magnet motors at low speed using transient finite-element analysis［J］.IEEE Transactions on Magnetics，2012，48（2）: 1003-1006.

［9］Yan Y，Zhu J G，Guo Y G.Initial rotor position estimation and sensorless direct torque control of surfacemounted permanent magnet synchronous motors considering saturationsaliency［J］.IETonElectricPower Applications，2008，2（1）:42-48.

［10］Gao W，Meliopoulos A P S，Solodovnik E V，et al.A nonlinear model for studying synchronous machine dynamic behavior in phase coordinates［C］//IEEE International ConferenceonIndustrialTechnology，HongKong，China，2005.

［11］Yan Y，Zhu J，Guo Y，et al.Numerical simulation of a PMSM model considering saturation saliency for initial rotorpositionestimation［C］//27thChinaControl Conference，Kunming，China，2008.

［12］Yi W，Jianguo Z，Youguang G.A Comprehensive analyticalmathematicmodelforpermanent-magnet synchronous machines incorporating structural and saturation saliencies［J］.IEEE Transactions on Magnetics，2010，46（12）:4081-4091.

［13］El-Serafi A M，Abdallah A S，El-Sherbiny M K，et al. Experimental study of the saturation and the crossmagnetizing phenomenon in saturated synchronous machines［J］.IEEE Transactions on Energy Conversion，1988，3（4）:815-823.

［14］Jansen P L，Lorenz R D.Transducerless position and velocity estimation in induction and salient AC machines［J］.IEEE Transactions on Industry Applications，1995，31（2）:240-247.

［15］Liang Xiaodong，El-Serafi A M，Faried S O.Application of the finite-element method for the determination of the parameters representing the cross-magnetizing in saturated synchronous machines［J］.IEEE Transactions on Energy Conversion，2010，25（1）:70-79.

［16］于月森，年长春，解光庆，等.负载不对称三相串联谐振逆变器电流平衡控制策略［J］.电工技术学报，2014，29（9）:49-53. Yu Yuesen，Nian Changchun，Xie Guangqing，et al. Current control strategy of three-phase series resonant inverter［J］.TransactionsofChinaElectrotechnical Society，2014，29（9）:49-53.

［17］ 耿乙文，伍小杰，周德佳，等.基于改进型比例谐振控制器的三相四线制光伏发电和有源滤波器系统［J］.电工技术学报，2013，28（8）:142-148. Geng Yiwen，Wu Xiaojie，Zhou Dejia，et al.Research on three phase four wire PV-AF system based on improved proportional resonant controllers［J］.Transactions of China Electrotechnical Society，2013，28（8）:142-148.

［18］ 王建伟，胡晓光，陈松松，等.动态电压恢复器的谐波补偿数字控制技术［J］.电工技术学报，2014，29（10）:239-245. Wang Jianwei，Hu Xiaoguang，Chen Songsong，et al. Harmonic compensation digital control technology of dynamic voltagerestorer［J］.TransactionsofChina Electrotechnical Society，2014，29（10）:239-245.

［19］Szalai T，Berger G，Petzoldt J.Stabilizing sensorless control down to zero speed by using the high-frequency current amplitude［J］.IEEETransactionsonPower Electronics，2014，29（7）:3646-3656.

Initial Position Estimation for Surface Permanent Magnet Synchronous Motors Based on Magnetic Saturation Effect

Tian BingAn QuntaoSun DongyangSun LiZhao Ke
（Department of Electrical EngineeringHarbin Institute of TechnologyHarbin150001China）

In this paper，the magnetic saturation model for surface permanent magnet synchronous motors（SPMSMs）is adopted to detect the initial rotor position.The model is also verified by the transient finite element analysis（FEA）method.The proposed algorithm is based on the injection of high-frequency（HF）rotating voltage vector，which produces the HF current response.Then this weak HF current is filtered and amplified significantly via a high pass and resonance filter which can also remove the DC components effectively.After that，an improved demodulation method is introduced to extract the useful information including the negative-sequence DC component and the iron core saturation evaluation function.The rotor direction is then estimated primarily via a phase-locked loop（PLL）with the extracted negative-sequence component and the magnetic polarity is furthermore confirmed via injecting a DC voltage vector at the estimated rotor direction and comparing the saturation evaluation function before and after.Overall the rotor position is estimated with the rotor direction and the magnetic polarity.The proposed initial position algorithm is validated by the 3.6 kW hardware drive system as well as on the Matlab/Simulink simulation platform using the suggested magnetic saturation model.It is proved to be simple，reliable，and with high precision.

SPMSM，initial position estimation，magnetic saturation effect，high pass and resonance filter，phase-locked loop

TM315

国家自然科学基金（51207029）、中国博士后科学基金（2012M510089、2014T70333）和黑龙江省博士后基金（LBH-Z11145）资助项目。

2015-01-14改稿日期 2015-11-10

田兵男，1989年生，博士研究生，研究方向为风力发电及电机控制。

E-mail:tianbing_hit@163.com

安群涛男，1984年生，副教授，硕士生导师，研究方向电机控制以及新能源发电技术。

E-mail:anquntao@163.com（通信作者）