基于拉氏变换的变温度PIN二极管动态建模

张佳佳　叶尚斌　张逸成　姚勇涛

（同济大学电子与信息工程学院　上海　201804）

基于拉氏变换的变温度PIN二极管动态建模

张佳佳叶尚斌张逸成姚勇涛

（同济大学电子与信息工程学院上海201804）

为了实现车载设备的传导噪声预估，二极管模型需在车载环境的宽温度变化范围内对动态特性进行准确描述。以PIN型功率二极管为研究对象，分析了定温度的拉式变换解析模型，引入温度参数，将原模型参数与温度的关系以函数的形式表达，实现任意结温下的模型参数温度修正，从而建立变温度的PIN二极管动态特性模型。在此基础上，通过温箱实验对感性负载条件下的功率二极管动态性能进行测试，实现了模型参数抽取和模型验证。结果显示，该模型在25～120℃的宽温度范围内，可实现反向恢复特性的精确模拟，各项特性参数的误差均较小，不会出现PSPICE通用模型的异常振荡问题，能满足宽频率及宽温度范围的汽车级EMI预估需求。

PIN二极管拉氏变换变温度模型

0　引言

电动汽车动力平台的二极管工作在高压、大电流的开关状态，其非理想动态开关特性，特别是反向恢复特性会对噪声产生重要影响［1，2］。因此，在进行EMI建模仿真预估时，采用的二极管模型不能仅满足静态和准静态需求，而应实现精确的动态开关特性仿真。

在电动汽车动力平台的高压大功率应用环境中，功率二极管多采用PIN结构［2］，即在重掺杂的n型和p型半导体中间夹一层较长的本征半导体Ⅰ层（即基区）。在常用的电路设计和仿真软件中，仿真模型多针对信号二极管或短基区二极管。这种模型无法准确描述PIN型长基区载流子浓度的变化，因此无法精确仿真PIN二极管的瞬态特性，有时甚至可能导致错误的结果［3，4］。

同时，车载设备所处的电磁环境的特殊性对二极管模型的准确度提出了更高要求。一方面，车载设备传导噪声频段为150 kHz～108 MHz，而工业用设备的噪声频段为150 kHz～30 MHz，因此汽车零部件级传导EMI预估中对二极管模型的动态特性仿真准确度需求更高。另一方面，汽车零部件的工作环境温度变化范围宽，而二极管的开关动态特性会明显受到温度的影响，因此完整的二极管模型应能反映温度对二极管动态特性的影响。总之，为了实现车载设备传导干扰的预评估仿真，需要一种可准确反映二极管温度特性的动态模型。

为了建立精确的PIN二极管动态模型，并使其在一定范围内保持适用性，多采用微观模型。即基于半导体内部的物理现象（如漂移、扩散、俄歇复合等），将载流子浓度的变化规律以多阶偏微分方程（即双极扩散方程）的形式进行描述和求解，并以数学或电路的形式表达［5］。

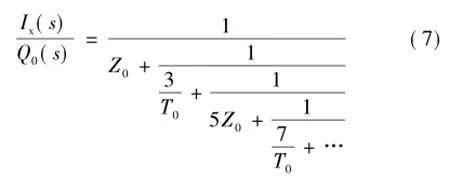
根据对双极扩散方程的不同求解方法，微观模型可分为数值模型、解析模型和混合模型。数值模型的核心思想［6］是采用数值计算的方法（如有限差分法以及TR离散化和牛顿-拉夫申线性迭代计算组合的方法等），对双极扩散方程进行精确求解。解析模型的重点是推导方程的解析解。具体措施包括:在时域引入集总电荷概念［7］将时间和空间的二维偏微分方程转换为不同空间位置处的多个时间微分方程，然后进行时域的等效求解；也可将时间参数转变为s域参数［8］，或将空间参数转变为频域参数［9］，经过域变换求解后再以电路进行等效。混合模型［10，11］则是将数值和解析模型进行组合，具体组合方式可分为交互式和包含式两类。

综合考虑模型的兼容性、精确度、参数获取难度等因素［6］，基于拉氏变换的解析模型更适合用于EMI预评估仿真。本文首先对PIN功率二极管定温度的部分拉式变换解析模型的拓扑形式与原理进行分析，并解释了模型参数的物理含义；然后从理论上分析了温度对该模型参数的影响，通过对模型参数表达式引入温度变量的方法，构建了各参数的温度修正函数，实现了可用于任意结温条件仿真的二极管变温度解析建模，并详细阐述了参数抽取方法。在此基础上，以MUR8100二极管为例，完成了二极管动态特性的变温度测试、参数抽取和模型验证，通过本文模型、PSPICE通用模型的仿真结果与温箱实验实测结果的对比，对本文模型的准确性、适用性以及相对于通用模型的优越性进行了验证。

1　定温的部分拉氏变换解析模型

根据突变空间结的耗尽近似假设以及大注入条件假设，可得描述基区载流子输运过程的双极扩散方程为

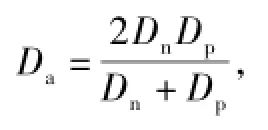
该方程的边界条件为

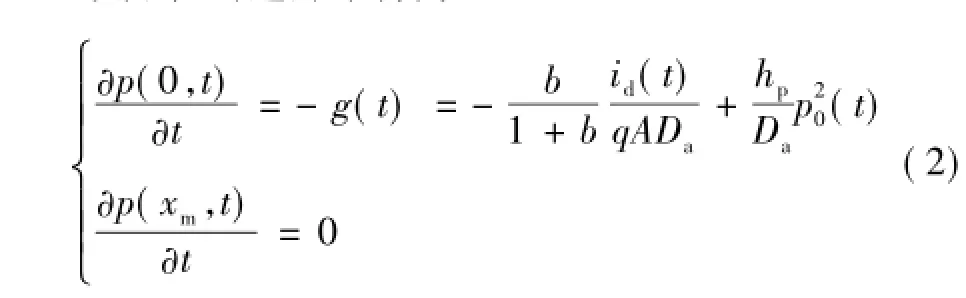
式中，g（t）为自定义的过渡变量；id（t）为流过二极管的电流；A为二极管的截面积；b为电子和空穴迁移率的比值，即μn/μp；hp为发射极复合系数；p0（t）为x=0处的载流子浓度；xm为常数，取值为w/2，其中w为基区宽度。严格来讲，当电子与空穴迁移率和发射效率均相等的理想条件下，基于对称的原理，xm才是常数w/2。但这种假设可极大地简化模型，且对整体模型的精确度影响不明显。

将式（2）进行改写，可得出以下表达式

式中，q0为x=0处的载流子浓度；ix为基区载流子注入产生的电流。于是，二极管电流可写为

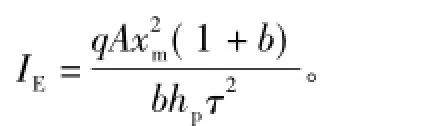
同时，基区左边界处的载流子浓度q0可根据玻尔兹曼关系与PN结的电压降联系起来。方程为

式中，IS、IKF和N均为模型参数。该方程的特性可利用PSPICE中的静态二极管模型内核进行描述，即图1中节点30、节点31和“地”构成的子电路部分，输出变量为流过二极管VDj的电流q0/τ。

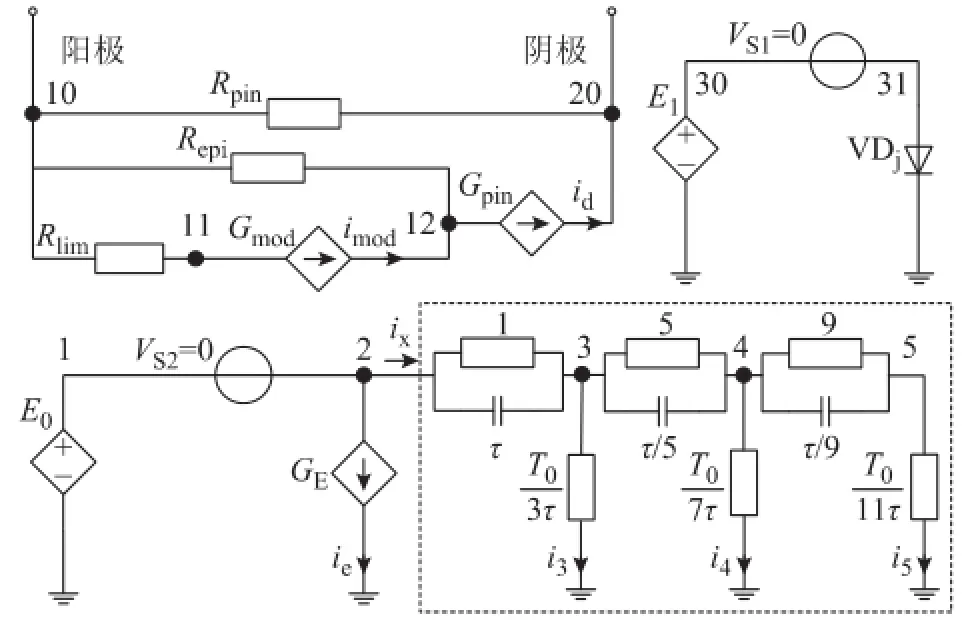
图1　PIN二极管的拉氏变换模型原理图Fig.1　Schematic diagram of Laplace-transform model for PIN diode

对式（1）～式（3）的时间变量进行拉氏变换，可得到载流子注入电流与基区左边界电荷量的比例关系为

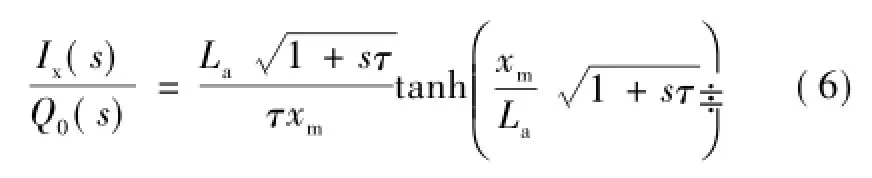
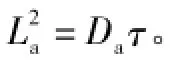
节点10和节点12之间的网络表征基区的电压降，涉及参数Rlim、Repi和Gmod。基区的电导压降为欧姆压降与Dember压降之和。Dember压降随电子与空穴迁移率差异的增大而增大。该电压通常远小于欧姆压降vepi，因此可忽略。定义 pave为基区的平均空穴浓度，ND为基区掺杂浓度，可得

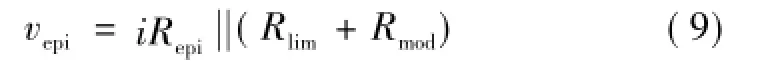
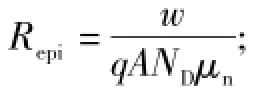
此外，在反向恢复过程的最后阶段，二极管两端出现反向电压，耗尽层边界会发生移动。然而对于高压二极管而言，击穿电压VPT通常非常大，而内建电动势PHI和空间电荷区等效电阻RSC非常小，边界移动效应可忽略［8］。因此，图1所示即为完整的定温PIN二极管模型，该模型的参数共9个，分别为τ、T0、Is、Repi、Rlim、IE、VM、N、IKF。

2　模型的变温度改进和参数抽取

半导体材料的特性参数（如载流子寿命τ、迁移率μ等）随温度变化，因此二极管外部特性会明显受温度影响。当温度不同时，二极管反向恢复时间、反向恢复电压/电流峰值等均不相同。因此，需要引入温度变量对模型加以改进，进而描述不同温度下二极管的动态开关特征。采取的方法是:通过分析定温模型参数的微观定义式，将其与温度的关系以函数的形式表达；以某温度（通常取25℃）的参数为基准，构建任意温度下的模型函数，并在PSPICE中利用程序语言进行描述。下面对各参数的温度特性进行详细分析。

1）τ和T0强烈依赖于温度Temp，且影响因素较为复杂，可通过测试的方式获得这两个变量随温度变化的曲线。

载流子寿命τ抽取方法是测试感性负载条件下的反向恢复电流波形［12］，读取反向恢复电流过零时刻t0、电流下降至反向峰值的时刻t1和反向恢复过程结束时刻t2，由此确定储存时间ts=t1-t0、下降时间tf=t2-t1和反向恢复时间 trr=t2-t0，那么可按照式（10）对τ进行计算。

2）二极管饱和电流IS的影响因素包括本征载流子浓度ni、掺杂浓度和二极管截面积，其中ni对温度敏感。由于 IS与 n2i呈正比，于是 IS随温度变化的函数［13］为

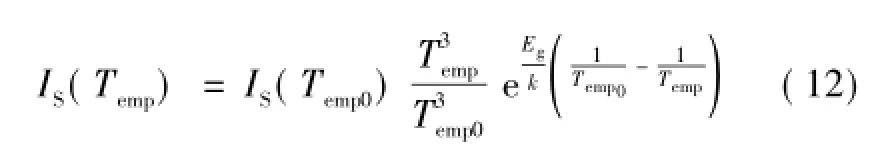
式中，Temp0为基准温度；Temp为待计算参数对应的温度；Eg为能带间隙；k为玻尔兹曼常数。由于式（12）中指数项随温度变化较小，为了便于PSPICE程序计算，式（12）可近似为式（13）。

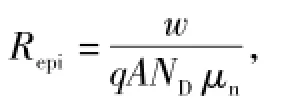
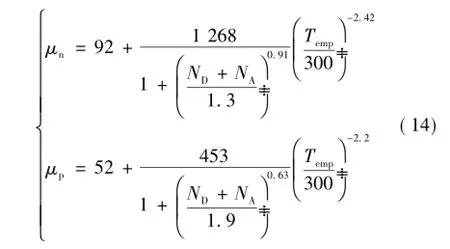
式中，ND和NA分别为掺杂的施主/受主浓度。由于μn和μp的数值一般较大，式（14）中的常数可忽略，由此得到简单的电子迁移率μn与Temp的关系，于是REPI的温度修正公式为

4）发射极复合拐点电流IE的表达式中，q、A、xm、hp均为常数，b=μn/μp。根据式（14）的经验公式可知，b对温度不敏感。于是，IE的温度函数由τ的温度函数确定，如式（16）所示。

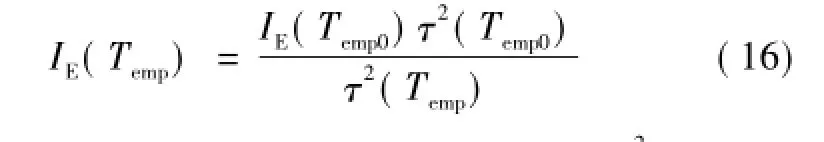
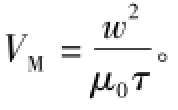
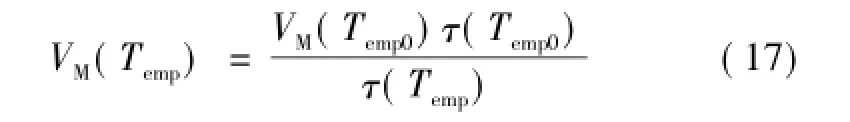
7）N和IKF是表征电流注入强度的参数，与基区轻掺杂的浓度和二极管工作的电流等级相关，不随温度变化。

根据以上分析，将对温度敏感的参数写为随温度变化的函数，即在原有模型参数基础上，增加温度变量Temp，除τ和 T0的温度函数需通过测试数据确定外，其他温度函数的形式和温度系数都是确定的，如式（12）～式（17）所示。于是，变温度PIN二极管模型参数抽取问题等效为基准温度（常温25℃）下定温模型参数的抽取。其中，τ和T0的抽取仍按式（10）和式（11）完成；其他参数则在温度修正函数的基础上，结合数据手册中不同温度下的静态曲线（通常为25℃和100℃）进行参数拟合。

3　二极管模型动态特性变温度测试验证

3.1动态特性测试方案与流程

为了进行模型参数抽取和变温模型验证，采用图2所示的感性负载测试电路，对PIN二极管的反向恢复电流波形进行测试。图中，DUT为待测的PIN二极管；MOSFET型号为 SPW16N50C3，开关频率为50 kHz，占空比为0.75。此外，为了测试不同温度下的DUT特性，将DUT固定在较大的铝制散热器上，制作二极管引脚延长线，使得二极管与测试电路其他部分分离，从而将含散热器的二极管单独放入温箱中，实现工作环境温度的控制。该引线的阻抗通过阻抗分析仪测量，并利用合适的等效模型进行描述，即图2中的线束寄生参数，通过这样的方式在电路仿真中考虑引线的影响。

图2　PIN二极管动态性能测试与仿真电路Fig.2　Test and simulation circuit for dynamic performance of PIN diode

按照图3所示的流程，测试25～120℃温度范围内的DUT反向恢复电流，每隔约10℃记录一组数据。由于散热器的热容量较大、静置时间较长，且上电时间较短，可认为每组数据对应的壳温Tc与环境温度Temp2一致，结温Tj与壳温Tc的温差可根据实际二极管的功率以及数据手册中的热阻RθJC进行推算，由此确定每组测试数据对应的结温Tj。

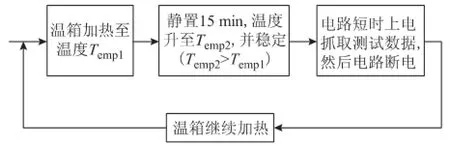
图3　PIN二极管动态性能温箱测试流程Fig.3　Procedure of temperature chamber measurement of PIN diode dynamic performance

3.2测试结果与模型验证

DUT的型号为MUR8100，持续正向电流最大值为8 A，反向承受电压最大值为1 000 V，热阻最大值为1.5℃/W。图4为该款二极管数据手册中给出的热响应曲线。测试到的二极管瞬时功率峰值P约为P= pk=4.0 A×1 V=4.0 W，二极管工作占空比为1-0.75=0.25，二极管导通时间为20 μs×0.25=5 μs，于是可根据曲线估算归一化的热阻系数r（t）为0.18，因此，结温 Tj与壳温 Tc间的温差 TJC=4×0.18× 1.5=1.08℃。该值相对于环境温度非常低，于是可将该温升忽略，近似认为抓取的数据对应的二极管结温Tj等于壳温Tc。

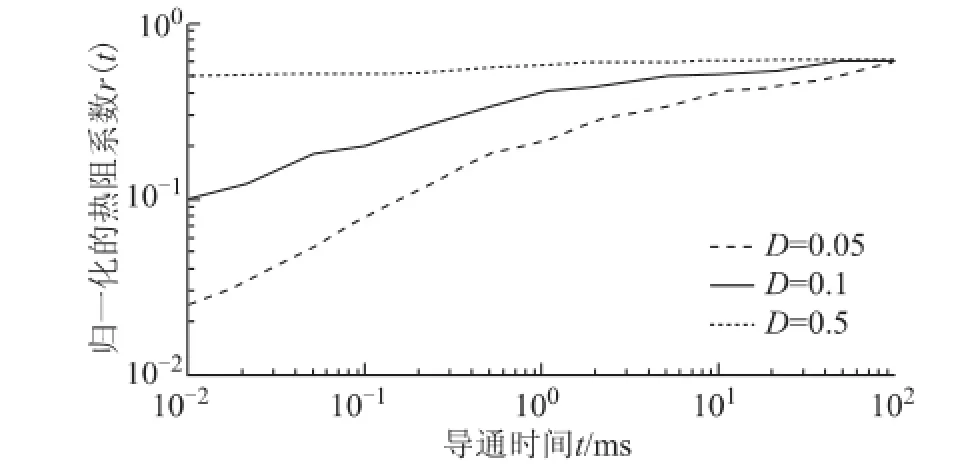
图4　MUR8100的热响应曲线Fig.4　Thermal response curve of MUR8100

图5为10种结温条件下MUR8100的反向恢复电流测试结果。从图中分别读取电流过零时刻t0、电流下降至反向峰值IRRM的时刻t1、反向恢复过程结束时刻t2、储存时间ts、下降时间 tf和反向恢复时间trr；在此基础上，根据式（10）和式（11）提取不同温度条件的模型参数τ和T0，结果如图6所示。

图5　反向恢复电流测试结果Fig.5　Test results of reverse recovery current

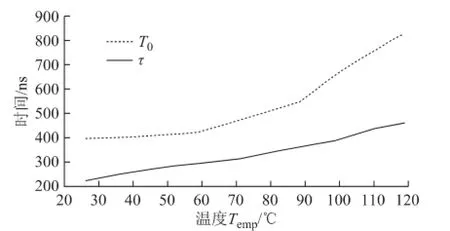
图6　模型参数τ和T0随温度变化的测试结果Fig.6　Test results of model parameter τ and T0when temperature varies

然后，在MATLAB软件中进行最小二乘拟合，拟合得到的静态特性曲线如图7所示，拟合数据与datasheet数据的均方差为0.019。此时参数拟合结果为:IE=49.999，IKF=0.143，N=1.837，Is=10-6，VM=0.266，Rlim=0.047，Repi=1.963。

图7　静态特性曲线仿真结果Fig.7　Simulated results of static characteristic curve

图8　反向恢复电流仿真结果Fig.8　Simulated results of reverse recovery current

根据拟合得到的模型参数基准值和各参数的温度修正函数，可得到完整的变温度PIN二极管动态模型。将该模型置于图2所示的电路中进行仿真，获得不同温度下的反向恢复电流波形，结果如图8所示。

为了进行定量分析验证，从图8的仿真结果中，读取电流反向峰值IRRM、储存时间ts、下降时间tf和反向恢复时间trr，并将其与图5中对应温度下的测试结果进行对比，结果列于表1中。

表1　不同温度下的MUR8100反向恢复过程参数测试与仿真结果对比Tab.1　Contrast of measured and simulated results of reverse recovery parameter of MUR8100 at different temperature

从表1中可看出，电流反向峰值IRRM的仿真结果偏大，仿真与测试结果的相对误差在3.7% ～7.7%；反向恢复储存时间ts仿真结果偏小，仿真与测试结果的相对误差低于5%，最小误差为1.9%；反向恢复下降时间tf的仿真结果偏大，仿真与测试的相对误差在6.2% ～10.9%；总反向恢复时间trr的仿真结果偏大，但相对误差低于2%，准确度非常高。从整体来看，表1中各参数的仿真和测试结果吻合度较高，不仅相对误差较小，且各参数随温度变化的趋势一致，因此，本文建立的变温度 PIN二极管动态模型是准确的。

为了进一步说明搭建PIN二极管动态模型的必要性，分别用本文建立的拉氏变换模型和PSPICE软件包中通用的二极管模型进行常温下的反向恢复特性仿真，结果如图9所示。

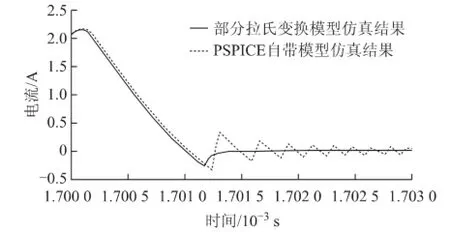
图9　不同模型的仿真结果对比Fig.9　Contrast of simulated results of different models

从图9中可看出，当二极管处于正向导通状态时，两个二极管模型的仿真结果较一致，均与图5中对应温度的测试结果吻合，说明两个模型在仿真二极管的静态和准静态特性时都是准确的。但在二极管由导通变为关断的反向恢复过程中，特别是反向恢复的下降阶段，PSPICE自带二极管模型的仿真结果出现异常振荡，二极管电流值不断在正负之间变化，与测试结果相差较大。

经分析，PSPICE中大功率电力二极管的自带 模型属于电荷控制型模型，其结构过于简单，只包含准静态电荷的分布模型。但反向恢复过程受动态电荷分布的影响更大，因此模型自身的准确性问题导致了这种异常振荡仿真结果［17］。本文建立的模型则是通过对载流子输运方程的拉氏变换求解实现的，即通过求解载流子浓度的动态变化来描述二极管的电流/电压变化，具有较高的准确度。

从时域的角度来看，PSPICE自带模型的仿真结果中，二极管并未正常截止。若二极管的工作周期短或占空比较大，那么前一个开关周期的仿真结果尚未进入稳定，就进入了下一个开关周期，从而导致较大的误差。从频域的角度来看，在这种异常振荡的频率附近存在较强的谐波，会给传导EMI仿真的频域结果带来较大误差。因此，在进行传导EMI预评估仿真时，特别是汽车零部件级的预估仿真时，需要采用本文的变温度的二极管动态特性模型代替PSPICE自带二极管模型，对二极管的反向恢复过程进行精确模拟。

4　结论

本文对PIN型高压功率二极管变温度模型的建立方法进行了研究，在定温的拉氏变换模型基础上，通过分析各参数的微观定义，引入温度变量，构建各参数变温度修正函数，从而建立了变温度的PIN二极管动态模型，实现对任意结温条件下的PIN二极管动态特性的精确仿真。

以MUR8100二极管为样品，进行了反向恢复过程的温箱实验，完成了变温度PIN二极管模型的参数抽取和准确性验证。通过测试与仿真结果的对比发现，本文模型在25～120℃的宽温度范围内均能实现高准确度的动态特性模拟，与实测结果吻合较高，并且仿真得到的动态特性随温度变化的趋势与测试结果保持一致，证明了本文模型能够精确模拟不同结温条件下的二极管的反向恢复过程。同时，本文建立的变温度模型不会出现PSPICE原模型的异常振荡现象，可满足汽车零部件级传导噪声预评估的仿真准确度需求。

［1］易荣，赵争鸣，袁立强.高压大容量变换器中快恢复二极管的模型［J］.电工技术学报，2008，23（7）: 62-67，80. Yi Rong，Zhao Zhengming，Yuan Liqiang.Fast recovery diode model for circuit simulation of high voltage high power three level converter［J］.Transactions of China Electrotechnical Society，2008，23（7）:62-67，80.

［2］李方正，徐勤富，赖建军，等.PiN二极管的一种改进型 PSPICE模型［J］.电工技术学报，2011，26（1）:172-176. Li Fangzheng，XuQinfu，LaiJianjun，etal.An improved powerPiNdiodemodelforPSPICE［J］. Transactions of China Electrotechnical Society，2011，26（1）:172-176.

［3］方春恩，李威，李先敏，等.PIN型功率二极管动态特性物理模型参数提取［J］.电工技术学报，2015，30（6）:208-215. Fang Chunen，Li Wei，Li Xianmin，et al.PIN power diodedynamicbehaviorandphysics-basedmodel parameter extraction method［J］.Transactions of China Electrotechnical Society，2015，30（6）:208-215.

［4］汪建民.PSPICE电路设计与应用（第2版）［M］.北京:国防工业出版社，2010.

［5］Bellone S，Della F，Benedetto D，et al.An analytical model of the switching behavior of 4H-SiC PIN diodes from arbitrary injection conditions［J］.IEEE Transactions on Power Electronics，2012，27（3）:1641-1652.

［6］张逸成，张佳佳，韦莉，等.用于电磁干扰预评估的功率PIN二极管建模研究进展［J］.同济大学学报（自然科学版），2015，43（4）:617-624. Zhang Yicheng，Zhang Jiajia，Wei Li，et al.Research progress of power PIN diode model for electro-magnetic interference pre-evaluation［J］.Journal of Tongji University（Natural Science），2015，43（4）:617-624.

［7］Cliff M，Lauritzen P，Sigg A.Modeling of power diodes with the lumped charge modeling technique［J］.IEEE Transactions on Power Electronics，1997，12（3）:398-405.

［8］Strollo A.A new SPICE model of power PIN diode based on asymptotic waveform evaluation［J］.IEEE Transactions on Power Electronics，1997，12（1）:12-20.

［9］Bryant T，Lu L，Santi E，et al.Physical modeling of fast pin diodes with carrier lifetime zoning，part 1:Device model［J］.IEEE Transactions on Power Electronics，2008，23（1）:189-197.

［10］Igic M，Mawby A，Towers S，et al.New physically based pin diode compact model for circuit modeling applications［J］.IEE Proceedings of Circuits Devices and Systems，2002，149（4）:257-263.

［11］Buiatti M，Cappelluti F，Ghione G.Power PiN diode model for PSPICE simulations［C］//20th Annual IEEEApplied Power Electronics Conference and Exposition，Austin，TX，2005，3:1911-1916.

［12］崔国庆，王建华，黄庆安，等.PIN二极管少子寿命测试方法［J］.电子器件，2004，27（2）:236-240，231. Cui Guoqing，Wang Jianhua，Huang Qing’an，et al. Measurement for minority lifetime in PIN diodes［J］. Chinese Journal of Electron Devices，2004，27（2）: 236-240，231.

［13］孟庆巨，刘海波，孟庆辉.半导体器件物理［M］.2版.北京:科学出版社，2009.

［14］ （美）Donald N.半导体物理与器件［M］.4版.北京:电子工业出版社，2013.

［15］陈治明，王建农.半导体器件的材料物理学基础［M］.北京:科学出版社，2003.

［16］Jayant J.功率半导体器件基础［M］.韩郑生，等译.北京:电子工业出版社，2013.

［17］Cher M T，King J T.Using power diode models for circuit simulations-a comprehensive review［J］.IEEE Transactions on Industrial Electronics，1999，46（3）: 637-645.

Temperature-variable Dynamic Modeling of PIN Diode Based on Laplace Transform

Zhang JiajiaYe ShangbinZhang YichengYao Yongtao
（Department of Electronics and Information EngineeringTongji UniversityShanghai201804China）

In order to realize the pre-evaluation of conducted noise of on-board equipment，it is necessary for the diode model to describe the dynamic characteristic accurately at wide range of temperature within on-board environment.By choosing the PIN power diode as the research object，the constant temperature Laplace transform analytical model is firstly established.By introducing the temperature parameter，the relationship between the parameters of the origin model and the temperature is expressed as a function.Thus the temperature correction of the model parameters is realized at any junction temperature，and a temperature-variable dynamic characteristic model for PIN diode is built.On this basis，the dynamic performance of the power diode is tested with the inductive load by the temperature chamber experiment.The model parameter extraction and the model verification are also realized.It is shown that，within the temperature range from 25℃ to 120℃，this model is accurate for the reverse recovery characteristic simulation with relatively small errors，and the abnormal oscillation of the PSPICE general model no longer exists.So the on-board EMI pre-evaluation requirements of wide frequency and temperature range are satisfied.

PIN diode，Laplace transfer，temperature-variable model

TN312.4

国家高技术研究发展（863）计划资助项目（2011AA11A265）。

2015-07-14改稿日期 2015-11-10

张佳佳女，1989年生，博士研究生，研究方向为大功率电能变换装备电磁兼容建模与设计。

E-mail:1989laurazhang@tongji.edu.cn（通信作者）

叶尚斌男，1990年生，博士研究生，研究方向为大功率电能变换装备电磁兼容建模。

E-mail:ysb1990712@163.com