两向正交正放网架结构传感器布置研究

王 欢，张丽梅，刘卫然，夏昌浩（河北科技大学建筑工程学院，河北石家庄 050018）

两向正交正放网架结构传感器布置研究

王 欢，张丽梅，刘卫然，夏昌浩
（河北科技大学建筑工程学院，河北石家庄 050018）

为了找到两向正交正放网架结构传感器的布置方法，针对模态可观测性与损伤可识别性传感器布置结果不一致的特点，由结构运动方程出发，考虑结构响应与振型和损伤灵敏度之间的关系，根据Fisher信息熵原理，建立同时包含模态振型和损伤灵敏度信息的Fisher信息矩阵，确立以Fisher信息矩阵2－范数最大化为准则的目标优化算法，构建了目标函数NC值，在完好、单损伤和多损伤情况下，通过该方法获得该结构的传感器布置方案。

传感器；两向正交正放网架；损伤灵敏度；Fisher信息矩阵；传感器布置

大跨空间结构具有结构合理、便于工业化生产、形式多样化、自重轻等优点，应用越来越广泛[1]。两向正交正放网架是网架结构中的常见形式，广泛应用于各项工程中[2]。随着使用时间的延长，一些结构不可避免地会出现杆件损伤问题，可能会引起整个结构的突然失效甚至坍塌[3]，严重威胁人们的财产安全。因此，如何对正在使用的结构进行实时监测，找到其损伤的部位和程度，具有一定的现实意义[4]。

目前网架结构健康监测以动测方式为主，一般包括监测设备的性能、传感器的布置、采集数据的有效性、安全评价及决策4个部分[5－13]。作为动测第1步的传感器布置，人们对这方面的研究主要有以下几方面：1）基于模态的传感器布置方法，如KAM－MER[14]提出的有效独立法（EI，effective independence algorithm）；2）基于损伤的传感器优化布置方法，如COBB等[15]研究出了模态数目、损伤程度与传感器数目三者之间存在的相互关系，SHI等[16]也提出了一种考虑损伤灵敏度的传感器布置方法。上述方法只是单一从模态或损伤角度对传感器布置问题进行了阐述，对于一些大型结构，如杆件较多的网架结构，单一从模态或损伤角度布置的传感器结果并不一致。

本研究找到了一种Fisher信息矩阵。此矩阵可以在考虑损伤对传感器布置影响的同时考虑到模态对传感器布置的影响，最终建立Fisher信息矩阵2－范数循环过程中最大值的判定准则。本文以一个两向正交正放网架结构为例来说明具体的实施过程。

1　网架结构传感器布置理论分析

1.1动力分析

N个由由度体系的自由振动动力学方程[3]为式中分别表示位移、速度和加速度向量；M，K，C分别为质量、刚度和阻尼矩阵。

在考虑小阻尼情况下，

假定结构损伤只会引起自身刚度的变化，则结构刚度发生一个小的扰动后，式（2）可表示为（3）

忽略式（3）里面的二次项，表达式可以变成

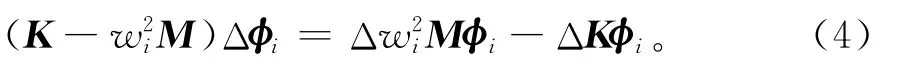
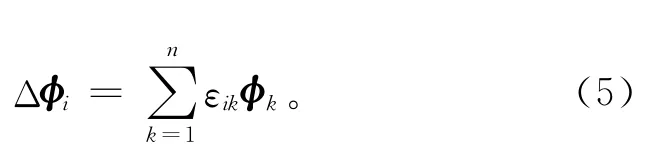
式中：εik为重因子；n为选取的模态数目。

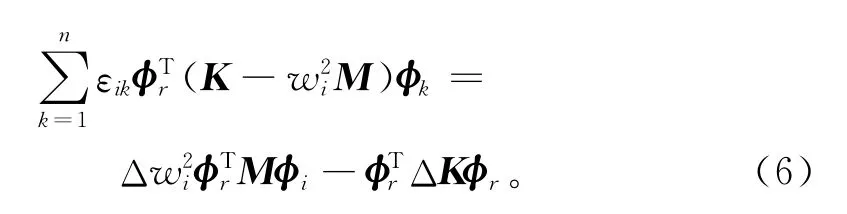
根据模态振型正交化的性质，式（5）可以表示为

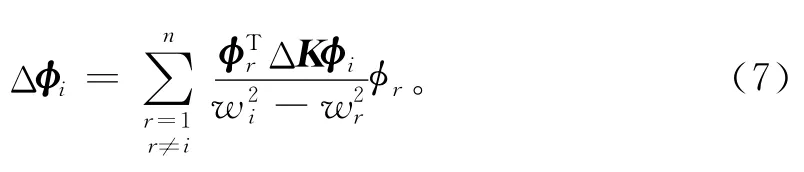
假定结构刚度的变化是每一个单元刚度变化的线性之和，则ΔK可表示如下：

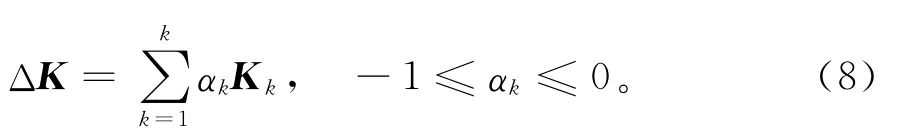
式中：αk为k单元的损伤系数；Kk为单元的刚度矩阵。

将式（8）代入式（7）后可以得到结构第i阶振型变化的具体表达式：

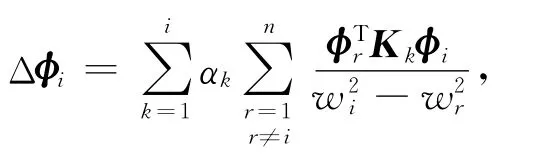
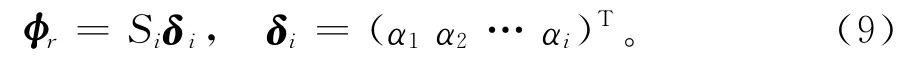
式中：Si为结构损伤后的第i阶损伤灵敏度；δ为结构单元损伤向量。

通过式（9），结构所有阶次上的振型改变矩阵ΔΦ可以表示为系统的振动模态展开式可以表示为

式中：U为损伤前的反应向量；Φ为结构发生损伤以前的振型矩阵；q为结构发生损伤以前的坐标向量。

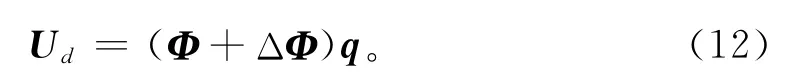
损伤后，结构的动力响应表达式改变为式中：Ud为损伤后的反应向量；ΔΦ为结构损伤后振型矩阵变化值。

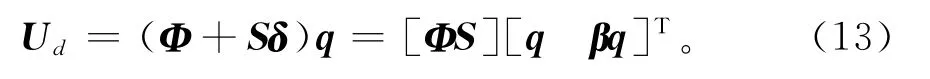
结构的动力响应受观测噪声影响后，表达式可变为

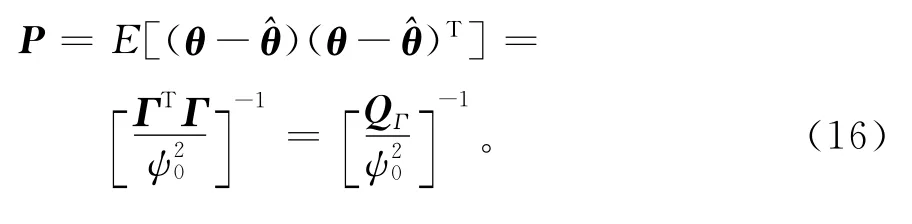
式中QΓ为Fisher信息矩阵，一阶近似表示为

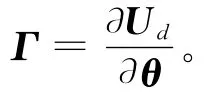
由式（16）可见，如果想使θ获得良好的估计，则只有使协方差矩阵P最小，而此时QΓ只有最大才能使协方差矩阵P最小，进而获得θ的最佳估计。

1.2传感器布置方法

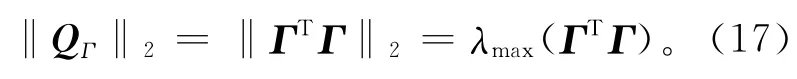
根据矩阵范数的定义可知，QΓ的2－范数为表示的是QΓ的最大特征值。由式（17）可知，当QΓ的2－范数取得最大值时就可以保证QΓ的最大化。所以传感器布置的目的就是使Fisher信息矩阵的2－范数取得最大值。

在所有自由度内循环，每循环一次得到一个2－范数normi。为表示每个自由度对Fisher信息矩阵的贡献值大小，建立方程式：式中NCi表示第i个自由度的贡献。

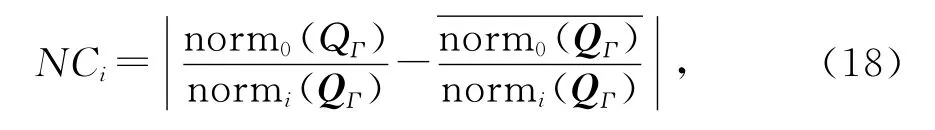
传感器布置步骤如下：第1步，通过ANSYS软件建模分析得到每一阶模态振型向量；第2步，根据振型向量构造Fisher信息矩阵，在此基础上建立Fisher信息矩阵的2－范数，在所有自由度内循环，每循环1次得到一个2－范数值；第3步，根据矩阵2－范数初始值norm0（QΓ）和循环得到值normi（QΓ），构建目标函数NC。目标函数NC取得最小值时对应的位置，即为所要的传感器的测点位置。

2　数值算例

以一个两向正交正放网架模型为例（如图1所示，图1中括号外的数字为上弦节点号，括号内的数字为下弦节点号），网架高度为2m，此模型共348个节点（上弦176个，下弦172个），1 139个单元，选用link8单元，钢材密度为7 850kg／m3，弹性模量为2.06×1011Pa，泊松比μ＝0.3，杆件截面面积为0.000 05m2。本模型下弦采用四周固定约束，考虑将传感器布置在下弦节点上。

图1　两向正交正放网架Fig.1 Two orthogonal spatial truss

设定的损伤情况有2种：1）单损伤情况，12杆损伤（连接节点13和14）30%；2）多损伤情况，12杆损伤30%和503杆（连接节点198和209）损伤40%。模型中通过改变截面面积来实现杆件损伤。

图2和图3表示模型中所有节点完好工况和单损伤工况的NC值分布图。可以看到：完好工况NC值局部最小值节点编号是261，262，263，264，265，266，267，268这8个点，其中267是最小值点；单损伤工况NC值局部最小值节点编号是256，257，258，259，260，261，262，263这8个点，其中259是最小值点。图2中完好工况和单损伤工况的图形略有差异，2种工况的最小值点取值不同，但是其最小值点的间隔不远。

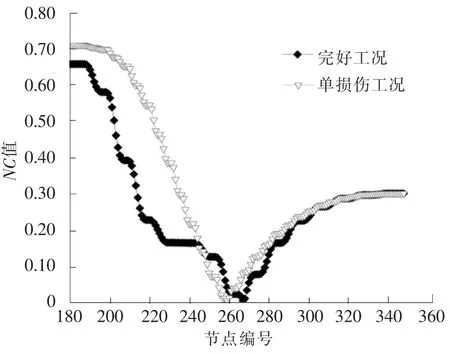
图2　完好和单损伤工况NC值Fig.2 NCvalues of intact and single damage mode

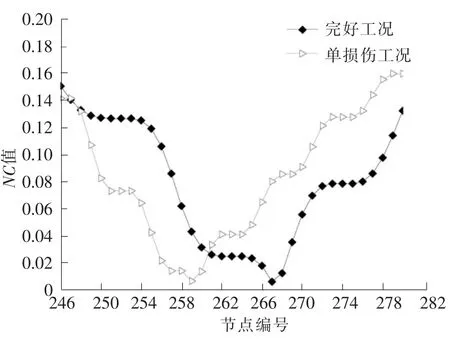
图3　图2中最小值部分局部放大图Fig.3 Smallest part of the local enlargement in fig.2

图4和图5是完好工况和多损伤工况NC值分布图，完好工况的NC值局部最小值的节点编号还是261，262，263，264，265，266，267，268这8个点；多损伤工况NC值局部最小值的节点编号是256，257，258，259，260，261，262，263这8个点，其中259是最小值点。

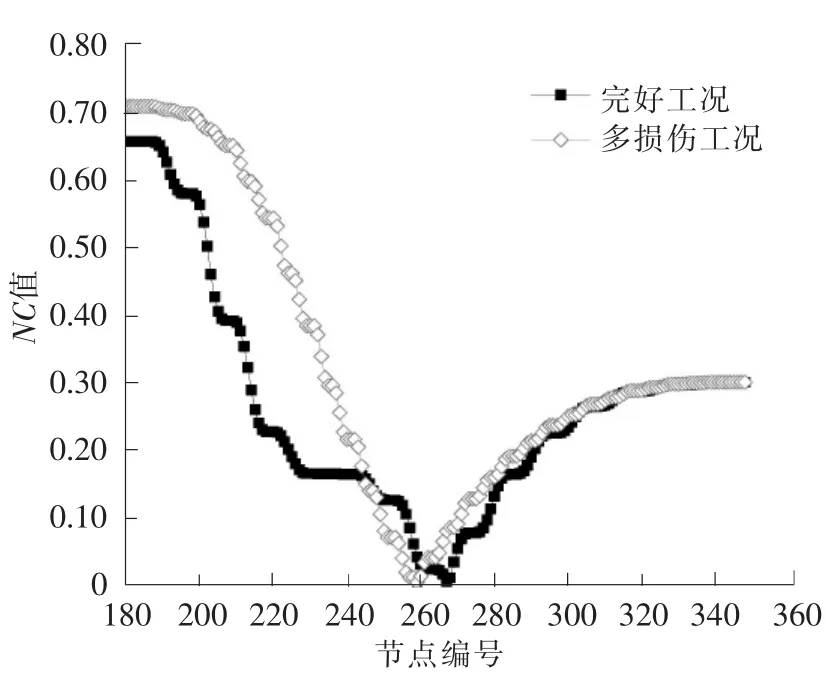
图4　完好和多损伤工况NC值Fig.4 NCvalues of intact and multiple damage conditions

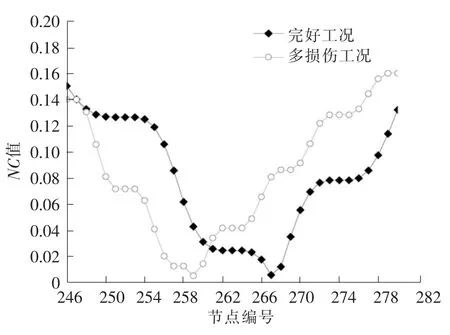
图5　图4局部放大图Fig.5 Local enlargement of fig.4

比较图2和图4可以发现：1）完好工况的NC值局部最小值的节点编号是261，262，263，264，265，266，267，268这8个点，不论单损伤工况还是多损伤工况，其NC值局部最小值点的位置都是256，257，258，259，260，261，262，263这8个点；2）损伤工况和完好工况的图形中，NC值最小值点存在一点儿差异，说明损伤对传感器布置有一定的影响。但是可以通过选取完好工况NC值局部最小值点包括损伤工况NC值最小值点来考虑损伤对传感器布置的影响。因此可以选取完好工况中258，259，260，261，264，265，266，267这8个点来作为传感器布置点，正好这8个点中267是完好工况NC值最小值点，259是损伤工况NC值最小值点，这8个点考虑了完好工况和损伤工况。

3　结 语

本研究找到了两向正交正放网架结构传感器的布置方法，并以一个348个节点的两向正交正放网架结构模型为例进行分析，对结构的完好和单、多损伤工况进行数值模拟，通过该方法获得了这个模型的传感器布置结果。结合网架结构的模态振型位移信息和经验分析可知，最终找到的传感器布置结果有较强的应用性。

／References：

[1] 沈世钊.大跨空间结构的发展——回顾与展望[J].土木工程学报，1998，31（3）：5－14.SHEN Shizhao.Development of large space structures：Review and outlook[J].China Civil Engineering Journal，1998，31 （3）：5－14.

[2] 占孟秦.两向正交正放网架抗火性能浅析[J].建筑安全，2014（6）：45－48.ZHAN Mengqin.Two orthogonal grid being put fire resistance performance[J].Construction Safety，2014（6）：45－48.

[3] 燕静静.正放四角锥网架结构单点激励位置选取和传感器布置研究[D].石家庄：河北科技大学，2013.YAN Jingjing.Study of Single Excitation Position and Sensors’Layout on Square Pyramid Space Grid Structure[D].Shijiazhuang：Hebei University of Science and Technology，2013.

[4] 范梦.考虑随机缺陷的网架结构损伤识别[D].石家庄：河北科技大学，2014.FAN Meng.Damage Identification of Space Truss Structures with Random Defects[D].Shijiazhuang：Hebei University of Science and Technology，2014.

[5] REN L，LI H，ZHOU J，et al.Development of health monitoring system for ocean offshore platform with fiber bragg grating sensors[C]／／Proceedings of the 15th Inte－rnational Offshore and Polar Engineering Conference.Seoul Cupertino：International Society Offshore Polar Engineers，2005：424－428.

[6] 张启伟，袁万城，范立础.大型桥梁结构安全监测的研究现状与发展[C]／／中国土木工程学会桥梁及结构工程学会第十二届年会论文集（下册）.广州：中国土木工程学会桥梁及结构工程学会，1996：576－581.

[7] 张启伟.大型桥梁健康监测概念与监测系统设计[J].同济大学学报（自然科学版），2001，29（1）：66－68.ZHANG Qiwei.Bridge health monitoring concepts and monitoring system design[J].Journal of Tongji University（Natural Science Edition），2001，29（1）：66－68.

[8] 熊海贝，李志强.结构健康监测的研究现状[J].结构工程师，2006，22（5）：86－90.XIONG Haibei，LI Zhiqiang.State of structural health moni－toring[J].Structural Engineer，2006，22（5）：86－90.

[9] 苏洁，张顶立.海底隧道结构健康监测研究[J].岩石力学与工程学报，2007，26（sup2）：3785－3792.SU Jie，ZHANG Dingli.Harbour tunnel structural health monitoring[J].Chinese Journal of Rock Mechanics and Engineering，2007，26（sup2）：3785－3792.

[10]郭彤，李爱群，李兆霞，等.大跨桥梁结构状态评估方法研究进展[J].东南大学学报（自然科学版），2004，34（5）：699－704.GUO Tong，LI Aiqun，LI Zhaoxia，et al.Research progress of span bridges state evaluation method[J].Journal of Southeast University（Natural Science Edition），2004，34（5）：699－704.

[11]杨玉冬，王浩，李爱群.大跨桥梁结构健康监测和状态评估研究进展[J].江苏建筑，2005（2）：18－26.YANG Yudong，WANG Hao，LI Aiqun.Research progress of span bridges in health monitoring and condition assessment [J].Jiangsu Building，2005（2）：18－26.

[12]邬晓光，徐宜恩.大型桥梁健康监测动态及发展趋势[J].长安大学学报（自然科学版），2003，23（1）：39－42.WU Xiaoguang，XU Yien.Bridge health monitoring dynamics and development trends[J].Journal of Chang’an University （Natural Science Edition），2003，23（1）：39－42.

[13]郑蕊，李兆霞.基于结构健康监测系统的桥梁疲劳寿命可靠性评估[J].东南大学学报（自然科学版），2001，31（6）：71－73.ZHENG Rui，LI Zhaoxia.Fatigue life reliability assessment of bridge structural health monitoring system[J].Journal of Southeast University（Natural Science Edition），2001，31（6）：71－73.

[14]KAMMER D C.Sensor placement for on－orbit modal identification and correlation of large space structures[J].AIAA Journal，1991，26（1）：104－121.

[15]COBB R G，LIEBST B S.Sensor location prioritization and structural damage localization using minimal sensor information[J].AIAA Journal，1996，35（2）：369－374.

[16]SHI Z Y，LAW S，ZHANG L M.Optimizing sensor placement for structural damage detection[J].Journal of Energy Machines，2000，126（11）：1173－1179.

Study of sensor placement on two orthogonal spatial truss structures

WANG Huan，ZHANG Limei，LIU Weiran，XIA Changhao
（School of Civil Engineering，Hebei University of Science and Technology，Shijiazhuang，Hebei 050018，China）

In order to find sensor placement method on two orthogonal spatial truss structures，considering the different placement of sensors for modal observability and damage identification，starting from the structural motion equation，taking into account the relationship between structural response and vibration mode and damage sensitivity，according to Fisher information entropy principle，the paper builds the Fisher information matrix which contains both the modal shape and the sensitivity information，and establishes a target optimization algorithm based on the maximum of 2－norm of Fisher information matrix.Then it constructs the objective NCvalue function.Sensor placement schemes are obtained by using the method with the structure in good condition are single or multiple damage condition，respectively.

sensor；two orthogonal spatial truss；damage sensitivity；Fisher information matrix；sensor placement

1008－1534（2016）01－0068－05

TU356

A

10.7535／hbgykj.2016yx01013

2015－10－01；

2015－11－08；责任编辑：张士莹

河北省自然科学基金（E2014208135）

王 欢（1987—），女，河北邯郸人，硕士研究生，主要从事网架结构传感器布置方面的研究。

张丽梅副教授。E－mail：zhanglimei168＠126.com

王 欢，张丽梅，刘卫然，等.两向正交正放网架结构传感器布置研究[J].河北工业科技，2016，33（1）：68－72.

WANG Huan，ZHANG Limei，LIU Weiran，et al.Study of sensor placement on two orthogonal spatial truss structures[J].Hebei Journal of Industrial Science and Technology，2016，33（1）：68－72.