有轨电车非接触感应耦合空心线圈的选型研究
吴 萍,罗 成,叶启舟
((1.中铁二院工程集团有限责任公司,四川成都 610031;2.西南交通大学,四川成都 610031)
有轨电车非接触感应耦合空心线圈的选型研究
吴 萍1,罗 成2,叶启舟2
((1.中铁二院工程集团有限责任公司,四川成都 610031;2.西南交通大学,四川成都 610031)
针对有轨电车非接触感应耦合电能传输系统的核心部分空心变压器空心线圈的选型进行分析和研究。首先对矩形空心线圈和圆形空心线圈的自感和互感进行计算,根据自感和互感计算出耦合系数。结合 Matlab 软件编程计算,对比分析 2 种空心线圈的耦合性能随初、次级线圈间隙、线径、初、次级线圈尺寸、初、次级线圈相同及不同尺寸下偏移量变化的影响。结果表明:在尺寸较大时,随着气隙、导线截面半径、线圈尺寸以及初、次级线圈相同尺寸下偏移量的增大,矩形线圈耦合性能都好于圆形线圈。反之,圆形线圈的耦合性能要好于矩形线圈。虽然随着初、次级线圈不同尺寸下偏移量的增大,圆形线圈耦合性能略好于矩形线圈,但其耦合系数远小于相同尺寸下的耦合系数。结合有轨电车大功率、大尺寸的条件,得出有轨电车适合采用初、次级线圈相同尺寸的矩形线圈。
有轨电车;非接触感应耦合;圆形空心线圈;矩形空心线圈
0 引言
随着交通拥堵、环境污染、城市规划等各种问题日渐突出,现代有轨电车作为一种运行可靠、舒适、节能、环保的城市轨道交通越来越受到各国的重视。许多城市改建或新增现代有轨电车线路,如法国巴黎、西班牙马德里以及我国的大连、天津、上海等城市[1]。而传统的接触式架空接触网供电一直存在噪声、磨损、设备腐蚀以及影响城市美观等问题[2],非接触式供电作为一种新型电能传输模式很好弥补了这些问题。与采用超级电容和蓄电池供电方式相比,超级电容和蓄电池的使用寿命有限、成本较高以及增加车体重量等问题,非接触式感应耦合供电方式显得更为优越。
非接触式感应耦合供电主要采用电磁感应耦合供电,电磁感应耦合供电是利用电磁感应原理,将供电线圈预先埋设在轨道下方,在车辆底部加设耦合线圈。车辆通过车载储能方式启动,在车辆运行过程中,供电线圈回路通电形成了电磁场,车底的耦合线圈不断切割磁感线,发生电磁感应,形成电流为车辆供电。同时还可为车载储能装置充电,方便车辆的下一次启动。
非接触感应耦合电能传输技术主要供电方式有3种:采用初、次级带铁心感应耦合;考虑到成本和复杂性,初级改用线缆,次级带铁心;考虑到铁心重量和成本,初、次级都采用空心线圈耦合。但空心线圈存在耦合性能不强且线圈形状多样等问题,为了提高能量传输效率,对于空心线圈的耦合性能的研究就显得非常重要。对于空心线圈已有一定的研究[4-10]。但对于有轨电车非接触感应耦合空心线圈的选型研究缺乏。
本文对非接触感应耦合变压器的矩形空心线圈和圆形空心线圈进行了计算对比分析,首先对矩形空心线圈和圆形空心线圈的自感、互感利用公式进行了计算,通过对比 2 种线圈的耦合性能随初、次线圈半径、气隙、线径、偏移量的影响,为适用于有轨电车的线圈进行选型。
1 空心线圈耦合计算
1.1 矩形空心线圈耦合计算

图1 单匝矩形线圈相对位置示意图
1.1.1 自感计算
如图1,初级单匝线圈长宽分别为 2l1和 2d,次级线圈长宽分别为 2l2和 2e,两线圈位置偏移量为 t,气隙宽度为 h,磁导率为 µ0,线圈导体截面半径为 R。线圈外自感利用磁通法对线圈 4 条有限长边进行积分获得,其初级单匝线圈外自感为[5]:

当线圈周长远大于线圈截面周长时,初级单匝线圈内自感可以表示为[5]:

所以,初级单匝矩形线圈的总自感为:
1.1.2 互感计算

2 个矩形线圈之间的互感可以通过计算 2 个线圈各导线之间互感之和而得到,利用聂以曼公式计算电感需要把矩形线圈分成几段直导线来考虑,然后对各直线导线之间运用公式进行计算[5]。
对于回路 1:

对于回路 2:

公式(4)、(5)中:dx1、dy1为初级线圈宽度和长度的微分, dx2、dy2为次级线圈宽度和长度的微分。
应用聂耳曼公式求解 a1、a2之间的互感为:

同理可以求得 Mb1b2、Mc1c2、Ma1c2、Mb1d2、Mc1a2。
所以,两单匝矩形线圈之间的互感 M 为:

1.2 圆形空心线圈耦合计算
1.2.1 自感计算
线圈自感为[3]:

公式(8)中:Le为线圈外自感,Li为线圈内自感。
如图2所示,r1为线圈平均半径,r 为导线内半径,l1为导线中心线,l2为导线内侧边线,θ 为 r 与 x 轴的夹角,Φ 为 r 和 r1之间的夹角。
线圈内自感公式为[3]:

根据聂以曼公式,线圈外自感公式[3]为:

推出外自感公式为:


图2 单匝圆形线圈自感计算
1.2.2 互感计算
如图3 所示,t 为初、次级线圈偏移量,h 为初、次级线圈气隙,r1、r2为初、次级线圈平均半径,l1、l2为初、次级线圈 1 匝的长度,r3为坐标原点到 dl2的距离。

图3 单匝圆形线圈相对位置示意图
根据聂以曼公式[3,4],线圈互感公式为:

推出互感公式为:

考虑到公式(7)和公式(13)互感中的积分式子无法用解析求解,因此,必须用双重积分定义求解积分的数值解。
2 空心线圈耦合系数的计算分析
耦合系数计算公式为:

公式(14)中:M 为初、次级线圈间的互感,L1、 L2为初、次级线圈的自感。
以下结合 Matlab 软件对空心线圈耦合性能作进一步分析。
2.1 耦合系数随初、次级气隙的变化
考虑到有轨电车的功率需求,设线圈导线截面半径 R= 5 mm,初、次级偏移量 t= 0 mm,参数见图4,则可以得到不同尺寸空心线圈间耦合系数 k 随气隙 h 变化的曲线,如图4 所示。

图4 耦合系数随气隙的变化曲线
由图4可以看出,耦合系数随初、次级线圈气隙增大下降得较快。且当线圈尺寸较小时,圆形空心线圈的耦合性能略好于矩形线圈。反之,矩形线圈略好于圆形线圈。
2.2 耦合系数随线圈导线截面半径的变化
设初、次级线圈导线截面半径为 R,为了和有轨电车实际相符,考虑了线圈导线直径,初、次级线圈气隙 h 取 20 mm,所取参数见图5,耦合系数 k 随线圈导线截面半径 R 的变化曲线如图5 所示。

图5 耦合系数随线圈导线截面半径的变化曲线
由图5 可以看出,当线圈尺寸较小时,耦合系数随初、次级线圈导线截面半径增大而增大,圆形空心线圈的耦合性能略好于矩形线圈。反之,矩形线圈耦合性能略好于圆形线圈,尤其在线圈导线截面半径小于 5 mm时,矩形线圈耦合性能好于圆形线圈。
2.3 耦合系数随线圈尺寸的变化
矩形线圈和圆形线圈初、次级线圈初始尺寸参数见图6,其中 l1st、l2st、est、dst、r1st、r2st为矩形线圈和圆形线圈初、次级线圈初始尺寸,在此基础上,同时按倍数增大初、次级线圈尺寸,得出耦合系数 k 随初、次级线圈导线尺寸增大倍数 m 的变化曲线,如图6 所示。

图6 耦合系数随线圈尺寸增大的变化曲线
由图6 可以看出,当线圈尺寸较小时,耦合系数 k随初、次级线圈导线尺寸的增大而增大,圆形空心线圈的耦合性能略好于矩形线圈。反之,随着尺寸的增大,矩形线圈耦合性能好于圆形线圈,尤其在线圈尺寸大于2 倍时,矩形线圈耦合性能远远好于圆形线圈。
2.4 初、次级线圈相同尺寸下耦合系数随偏移量的变化
线圈各参数见图7,初、次级线圈相同尺寸下耦合系数 k 随初、次级偏移量 t 的变化曲线如图7 所示。
由图7可以看出,初、次级线圈相同尺寸下,在线圈尺寸较小时,圆形线圈正对时的耦合性能好于矩形线圈,但随着偏移量的增加,圆形线圈耦合性能比矩形线圈差。当线圈尺寸较大时,矩形线圈耦合性能完全好于圆形线圈。
2.5 初、次级线圈不相同尺寸下耦合系数随偏移量的变化
前面的分析都基于初、次级线圈相同长宽基础上进行计算分析,当初、次级线圈长度不一样,取初级线圈尺寸为次级线圈尺寸的 2 倍时,各参数见图8,耦合系数 k 随偏移量 t 的变化曲线如图8 所示。
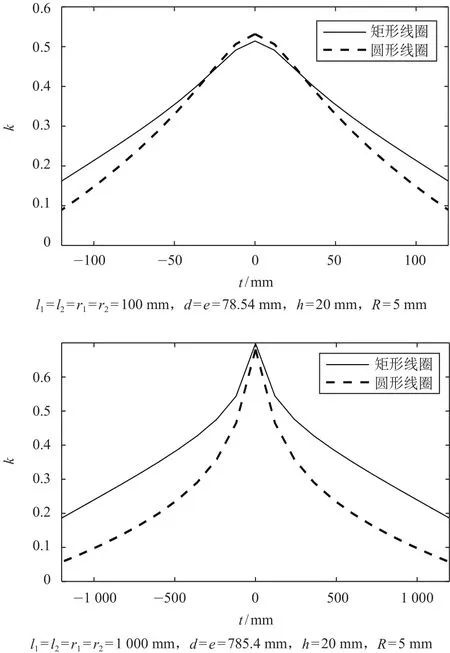
图7 初、次级线圈相同尺寸下耦合系数随偏移量的变化曲线
由图8 可以看出,耦合系数在一定偏移量范围内是较平稳的,基本不变。当初、次级线圈耦合系数在 t /2l1( t/2r1)= 0.25 时取得最大,也就是当次级线圈移动到边缘和初级线圈边缘正对的时候,耦合系数最大。而再增大偏移量时,其耦合系数随之减小。且圆形线圈的耦合性能都略好于矩形线圈。但相比于相同尺寸下的耦合性能差很多。
3 结论
本文对有轨电车非接触感应耦合的核心部分空心线圈进行了对比计算分析,推导出矩形和圆形空心线圈的自感和互感计算公式,探讨了不同尺寸下,初、次级线圈的气隙、导线截面半径、线圈尺寸、偏移量对 2 种线圈耦合性能的影响。结果表明,在尺寸较大时,随着气隙、导线截面半径、线圈尺寸以及初、次级线圈相同尺寸下偏移量的增大,矩形线圈耦合性能都好于圆形线圈。反之,圆形线圈的耦合性能要好于矩形线圈。虽然随着初、次级线圈不同尺寸下偏移量的增大,圆形线圈耦合性能略好于矩形线圈,但其耦合系数远小于相同尺寸下的耦合系数。所以,根据以上分析,结合有轨电车大功率、大尺寸的条件,得出有轨电车适合采用初、次级线圈相同尺寸的矩形线圈。

图8 初、次级线圈不同尺寸下耦合系数随偏移量的变化曲线
[1] 薛美根,杨立峰,程杰.现代有轨电车主要特征与国内外发展研究[J].城市交通,2008,6(6):88-91,96.
[2] 何治新.现代有轨电车牵引供电方式选择[J].城市轨道交通研究,2013(7):105-108,113.
[3] 冯慈璋,马西奎.工程电磁场导论[M].北京:高等教育出版社,2000.
[4] 刘修泉,曾昭瑞,黄平.空心线圈电感的计算与实验分析[J].工程设计学报,2008,15(2):149-153.
[5] 武瑛.新型无接触供电系统的研究[D].北京:中国科学院,2004.
[6] Chwei-Sen Wang, Oskar H Stielau, Govic.Design Considerations for a Contactlesselectric Vehicle Battery Charger[J].IEEE transactions on industrial electronics,2005,52(5):1308-1314.
[7] Jesús Sallán, Andrés Llombart, José Fco.Sanz.Optimal Design of ICPT Systems Applied to Electric Vehicle Battery Charge[J].IEEE transactions on industrial electronics,2009,56(6):2140-2149.
[8] O.H.Stielau,G.A.Covic.Design of Loosely Coupled Inductive Power Transfer Systems[J].IEEE Power System Technology,2000,l(l):85-90.
[9] 王小霞.非接触电能传输系统控制技术研究与实现[D].重庆:重庆大学,2009.
[10] 周雯琪.感应耦合电能传输系统的特性与设计研究[D].浙江杭州:浙江大学,2008.
责任编辑 冒一平
Study on Type Selection of Contactless Inductive Coupling Hollow Coil for Tram
Wu Ping, Luo Cheng, Ye Qizhou
The paper makes the tram calculation firstly of rectangular and circular hollow coil self inductance and mutual inductance, and then calculates the coupling coefficient.Based on the programming calculation of Matlab software, it also makes a comparative analysis on the coupling performance of two types of hollow coils of the primary and secondary coil gap, coil diameter, primary and secondary coil size, identical and difference of primary and secondary coil sizes under the influence of offset changes.The results show that when the size is larger,with the increase of the air gap, the cross section radius of conductor wire, the size of the coil and the offset of the same size of the primary and secondary coils, the coupling performance of the rectangular coil is better than that of the circular coil, but the coupling coeffi cient of the circular coil is smaller than that of the rectangular coil.With the increase of offset of the primary and secondary coils, the coupling performance of the circular coil is slightly better than that of the rectangular coil, but its coupling coeffi cient is much smaller than that of the same size.Under the condition of the high power and large size of the tram, the paper concludes that the tram is suitable for rectangular coil with same size for the primary coil and the secondary coil.
tram, contactless inductive coupling, circular hollow coil, rectangular hollow coil
U482.1∶U223.5
吴萍(1981—),女,高级工程师
2016-03-25

