问题打破预设 师生生成探究*

●孙小龙

(如皋市第一中学　江苏如皋　226500)



问题打破预设师生生成探究*

●孙小龙

(如皋市第一中学江苏如皋226500)

学生在教师预设之外提出有价值的探究性问题时，教师应珍惜这个贴近学生实际的探究性资源，并以此为契机，帮助学生建构循序渐进研究问题的思维模式，从而在探究中成长，在探究中提升学生数学学习的能力.

问题;预设;生成;探究

笔者任教的是江苏省四星级高中高二理科实验班，学生基础扎实，思维活跃，有很强的质疑精神，常在预设之外提出有价值的探究性问题.笔者欣喜之余，常果断放弃预设，与学生一起对质疑进行深入探索，共寻破解之道，共享探究之乐.如此，学生的探究体验不断丰富，在探究中成长，在探究中强化对三基的认识，在探究中品味数学学习的快乐.下面笔者谨以一节直线与圆复习课中“意外探究”与读者共享.

1　课前预设，触发问题

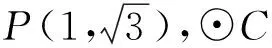
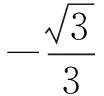
师：将上述问题推广到一般情况：点P(x0,y0)在⊙C:x2+y2=r2上，求过点P的⊙C的切线方程.

生2：与刚才的方法一样，可求得过点P的⊙C的切线方程为x0x+y0y-r2=0.

生3：还要考虑特殊情况：切线与直线PC中有一条斜率不存在的情况，即x0=0或y0=0，不过也满足切线方程x0x+y0y-r2=0.结合以上，所求的切线方程为x0x+y0y-r2=0.

师：虽然最后切线方程可以合二为一，但不考虑特殊情况，解题就有失严谨.有没有其他方法求切线方程？

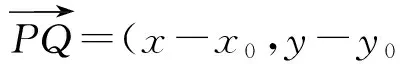
由PQ⊥OP可知

(x-x0)x0+(y-y0)y0=0

从而

x0x+y0y-r2=0.

师：很好，借助向量的数量积处理垂直问题，避免了特殊情况的讨论.大家仔细观察上面的切线方程与圆的方程之间有没有可以总结的规律？据此猜一猜经过圆(x-a)2+(y-b)2=r2上一点P(x0,y0)的切线方程应该是什么？

生5：规律是将圆方程中的平方表示成2个因式相乘的形式：其中一个x换成切点横坐标x0，一个y换成切点纵坐标y0，这样得到的二元一次方程即为切线方程.根据这个规律，经过圆(x-a2)+(y-b)2=r2上一点P(x0,y0)的切线方程应该是

(x0-a)(x-a)+(y0-b)(y-b)=r2.

师：很好，有理有据，猜想的结论也是正确的.可参考上面的2种方法进行证明.

笔者话音刚落，有学生站起来质疑：如果点P(x0,y0)不在圆上，那么这样表示的直线在哪儿？它与点P之间有什么联系呢？

(一石激起千层浪，教室里静悄悄的，学生陷入了沉思.)

2　放弃预设，生成探究

教师是该按照课前预设继续进行，以“这个问题大家课后思考”一句话带过，还是打破课前预设，与学生共同探讨呢？开展探究性学习是培养学生思维能力的重要渠道.文献[1]中提到取之于学生、来源于教学实际的探究性材料最适合学生，切合学生的知识水平和思维层次，学生参与度高，学生感觉自然、亲切、兴趣浓.这样的探究性契机稍纵即逝，非常宝贵，值得珍惜.略一思忖，笔者决定果断放弃课前预设，现场生成，与学生一起探究和体验.

师：这个同学问题提得非常好，出乎我的意料，我们一起来探究这个问题.现在不能立即确定直线的位置，但能否对这条直线的位置有个粗略地预判？

生6：如果点P在圆外，应该不是过点P的切线(因为过点P有2条切线，所以不可能只有1个方程).

生7：如果点P在圆内，过点P就没有切线；如果点P与圆心重合，那么方程(x0-a)(x-a)+(y0-b)(y-b)=r2就不表示直线了，我认为应该限制点P与圆心重合，这样方程才能表示直线.

师：很好，生7思考得很周到，将提出的问题进行完善，难能可贵.要确定这条直线的具体位置，可以通过研究这条直线的相关特征来定位.不妨先从简单的圆x2+y2=r2来研究直线l：x0x+y0y-r2=0的位置特征.

下面各小组先就点P(x0,y0)在圆外时进行讨论交流，并推荐一名代表发言.顿时教室内人头攒动，争论声此起彼伏，探究的快乐洋溢在学生的脸上.

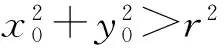
1)点P和圆心O的坐标均不适合方程x0x+y0y-r2=0，因此直线l不经过点P和圆心O；

2)由(x0·0+y0·0-r2)(x0x0+y0y0-r2)<0可得点O,P位于直线l的2侧.

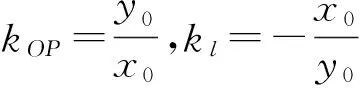
师：根据上述特征只能确定直线位置的粗略范围，仍不能具体确定直线的位置.

师：只是进一步缩小了范围，还不能确定，还需要进一步研究.

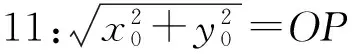
r2=d·OP，

即

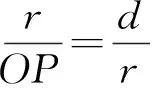
从而△OAP∽△OAC(如图1所示)，于是OA⊥AP，同理可得OB⊥BP，因此A,B为过点P的2条切线与⊙O的切点，故点A,B唯一确定，直线l也唯一确定.

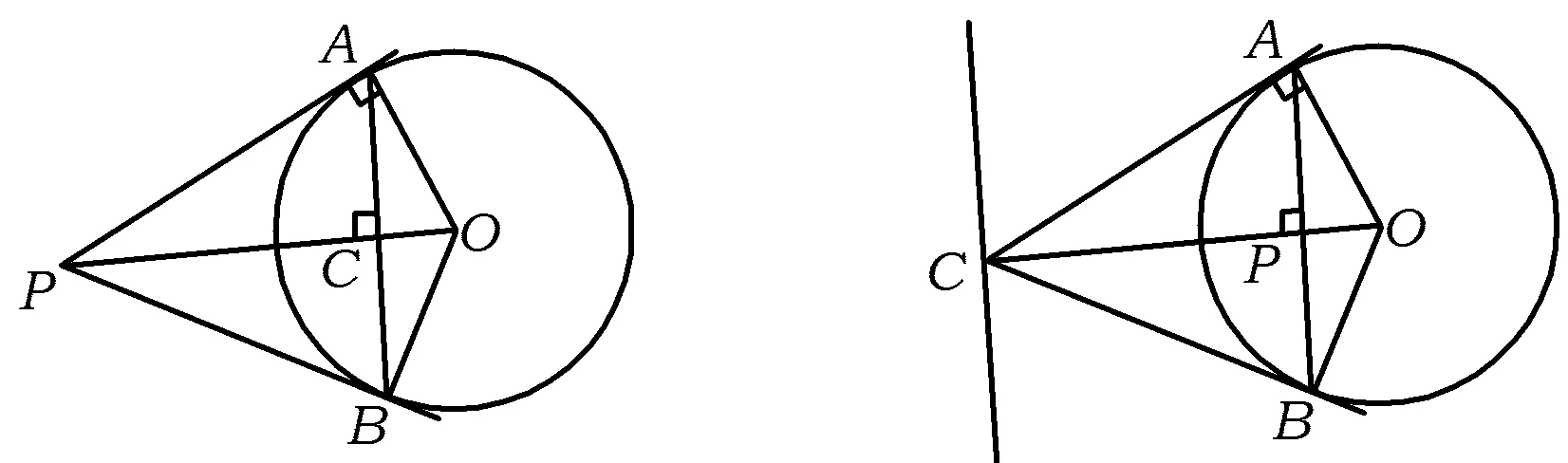
图1　　　　　　　　　　　　图2

师：真的很棒，为你们的探究喝彩，为你们的探究精神鼓掌！从上面的探究可知：当点P(x0,y0)在圆外时，x0x+y0y-r2=0表示的直线为过点P的2条切线的切点连成的直线，简称为切点弦所在的直线.

师：当点P(x0,y0)在圆内且不与圆心重合时，直线l：x0x+y0y-r2=0又在哪里？

各小组经过片刻讨论后，给出了如下类似的特征：

直线l不经过点O和点P；点O,P位于直线l的同侧；OP⊥l；直线l与⊙O相离；r2=d·OP.

根据上述特征便可确定直线l的具体位置：如图2，过点P作直线OP的垂线，交⊙O于点A,B，过点A,B作⊙O的切线交直线OP于点C，过点C作与OP垂直的直线即为方程x0x+y0y-r2=0表示的直线l.

3　问题再生，深度探究

生12：上述结论在课本上并没有，在填空题中可以直接加以使用，但解答题应该需要详细规范的推导过程，如何直接推导呢？

师：很好，那我们以具体的题目为例来探究直线l的推导过程.

例2已知⊙C:x2+y2-2x-4y-4=0外一点P(-4,-1)，过点P作圆的切线PA,PB，求过切点A,B的直线方程.

师：下面各小组交流讨论，派代表将解法展示到黑板上.

各小组探究的积极性得到了进一步的调动，争先恐后进行展示，笔者选择了其中有代表性的5种方法简略展示如下：

方法1(斜率+点)

如图3，联结AB交PC于点D，由对称性可知CP⊥AB，由PA是⊙C的切线可得AC⊥PA.⊙C的方程x2+y2-2x-4=0可化为

(x-1)2+(y-2)2=9，

图3

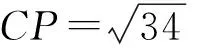
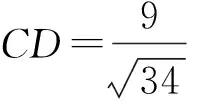
从而

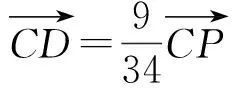
设D(x,y)，由向量等式可得

从而

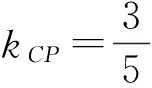
从而

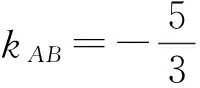
因此直线AB的方程为

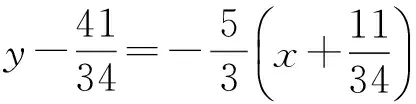
即

5x+3y-2=0.

方法2(斜率+d+取舍)

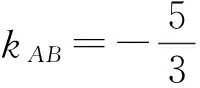
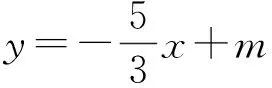
即

5x+3y-3m=0，

从而

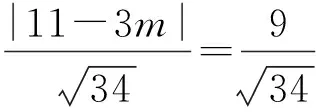
解得

3m=2或3m=20.

因为点P和点C位于直线AB的2侧，由线性规划可得

(11-3m)(-23-3m)<0，

从而

-23<3m<11，

于是3m=2，故直线AB的方程为

5x+3y-2=0.

方法3(相交弦法)

由PA=PB可得点A，B在以点P为圆心、PA为半径的圆上，从而直线AB为⊙C与⊙P的相交弦.由上述计算可知PA=5，⊙P的方程为

(x+4)2+(y+1)2=25，

结合⊙C的方程，可得直线AB的方程为

5x+3y-2=0.

方法4(相交弦法)

由图3可知，点A，P，B，C共圆，该圆以PC为直径，可得圆的方程为

(x+4)(x-1)+(y+1)(y-2)=0，

从而直线AB为⊙C与该圆的相交弦.结合⊙C的方程，可得直线AB的方程为

5x+3y-2=0.

方法5(方程思想)

设A(x1,y1)，B(x2,y2),由圆上一点处的切线方程可得直线PA的方程为

(x1-1)(x-1)+(y1-2)(y-2)=9，

此直线经过点P，从而

-5(x1-1)-3(y1-2)=9，

化简可得

5x1+3y1-2=0，

同理可得

5x2+3y2-2=0.

因此点A,B均满足方程

5x+3y-2=0，

方程5x+3y-2=0表示一条直线，而2个点确定一条直线，因此5x+3y-2=0即为直线AB的方程.

师：上面各小组从多个角度展示了直线l的求法，非常到位.课后自己设计一道点P在圆内的试题进行自我探究，相信你一定可以想到很多方法，一定会有更多收获.

4　教后思考

1)问题是数学的心脏.问起于题，疑源于思，正如亚里士多德所言“思维从疑问和惊奇开始”.学生有疑而问体现了一种求知欲，闪烁着智慧的火花.善疑勤问，有助于培养学生独立思考的能力.教师要把学生培养成一个有想法、敢质疑、会提问的积极思考者，要充分保护学生提问的积极性，对提出“优”问题的学生要大力表扬，鼓励学生有疑必问[2].一个好的问题必定来源于学生深层次的思考，让提问题、提好问题蔚然成风.让学生在问题的引领下巩固知识，根植方法，为持续学习注入动力，注入活力.

2)充分利用来源于教学实际的探究性资源.适时开展探究性学习，对提高学生思维能力的重要性毋庸置疑，实际操作起来最困难的是找不到适合学生的探究性材料，极易脱离学生的最近发展区，激发不起学生探究的兴趣，往往有其形而失其神[3].而来源于教学实际、取之于学生的探究性材料贴近学生实际，是学生有感而发的流露，学生感觉自然、亲切，此时学生的求知欲望最强烈，是开展探究性活动的最佳时机，效果不言而喻.教师要充分挖掘来源于教学实际(学生提问、学生作业等)的探究性资源，以此为契机，建构循序渐进研究问题的思维模式，增强学生自我破解问题的能力.

3)教师要有探究意识、探究精神.有了探究意识，教师才能抓住教学实践中值得研究的问题.有了探究精神，教师自身才能主动发现探究性材料，才能经常性地开展自我探究活动，才能分辨教学实际中有价值的探究，才能在探究中帮助学生修正数学学习的思维方式，对学生探究活动的指导才能够高屋建瓴，长此以往，必将潜移默化地提升学生的思维及解题能力.

[1]张昌盛．家常探究一条开展探究性学习的好渠道[J]．数学通报，2016(1)：43-46．

[2]赵娅芳.浅谈数学课堂生成教学的实施策略[J].中学教研(数学),2008(7):10-11.

[3]张健.新课程理念下的生成性教学及其实施策略[J].中学数学教学参考,2007(19):21-23.

*收文日期：2016-04-19；2016-05-25

孙小龙(1976-)，男，江苏如皋人，中学数学高级教师.研究方向：数学教育.

O123.1

A

1003-6407(2016)08-19-04