“等弧度三圆共点图”的几个有趣性质*

●黄新民

(温州市教育教学研究院　浙江温州　325000)



“等弧度三圆共点图”的几个有趣性质*

●黄新民

(温州市教育教学研究院浙江温州325000)

数学中有美，美中有数学.数学之美无处不在，探求数学之美，是广大数学爱好者乐此不疲的事.美丽的几何图形，往往蕴含着诸多美妙的数学性质.文章构造了一个漂亮的“等弧度三圆共点图”，并对其作深入探究，发现有许多有趣的性质.

等弧度;三圆共点图;四点共圆

数学之美无处不在，数学爱好者对数学内在美的探求孜孜不倦，乐此不疲.笔者最近在研究共点圆中，构造了一个漂亮的“等弧度三圆共点图”(如图1)，并发现图中蕴含着许多美妙的几何性质[1].

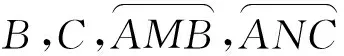
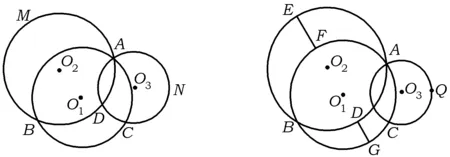
图1 图2

为叙述方便，先证明下面的结论：

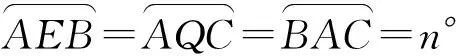
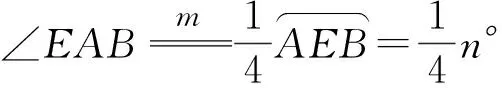
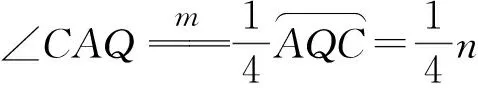
∠EAB+∠CAQ+∠CAB=180°，

即点E，Q，A共线.

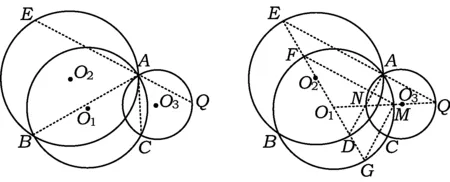
图3　　　　　　　　　图4

性质1的证明[3]因为点E，D，F，G分别是⊙O2，⊙O1上4段弧的中点，所以点E，D，F，G，O1，O2共线，以下分2种情况：

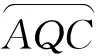
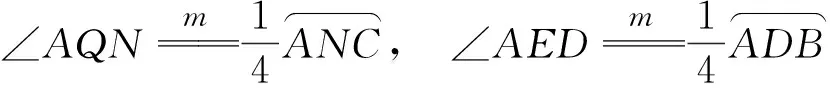
因此∠AQN=∠AED，O1Q=O1E,而O1F=O1M,故EF=MQ.

下证DG=MN.联结AN，AD，GM，因为NA⊥EQ，DA⊥EQ，所以点A，N，D共线.又FM∥QE，GM⊥FM，从而AD⊥FM,因此

AD∥GM.

由O1G=O1M，得DG=MN，即

EF+DG=NM+MQ=NQ(即⊙O3的直径).

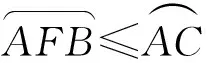
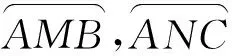
证明联结AB，AC，BC，AD，BO2，过点D分别作⊙O2，⊙O3的直径DG，DF，联结O1O2并延长交⊙O2于点E，联结O1O3并延长交⊙O3于点H，联结AG，AF(如图5).

因为DG，DF都是直径，所以

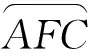
∠BAC=∠CFA，∠1+∠3=∠2+∠3,

所以

∠1=∠2，∠GO2B=∠AO3F.

由点E在O1O2的延长线上，点H在O1O3的延长线上，得

∠GO2E=∠HO3F，

即

∠O1O2D=∠O1O3D，

故点O1，O2，O3，D共圆.

图5　　　　　　　　　图6

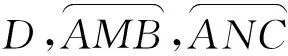
证明联结AB，AC，不妨设AB>AC，分2种情况：若割线经过点D，则点E，F都与点D重合，显然结论成立.当割线不经过点D时，分以下2种情况：

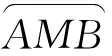
∠AEB=∠BAC=∠AFC,

从而

∠ACF+∠FAC=∠BAE+∠FAC,

因此

∠ACF=∠BAE.

又∠ACF=∠HGA,从而

∠HGA=∠BAE,

于是

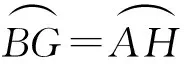
即

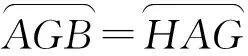
因此

AB=GH.

由△ABE≌△GHF知AE=FG,故

EG=AF.

图7　　　　　　　　　图8

∠BEA=∠AFC=∠GFH,

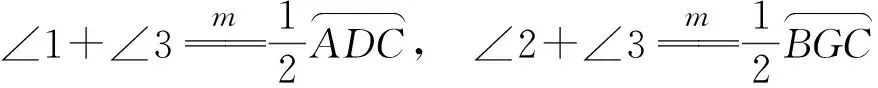
即

∠1+∠3=∠2+∠3,

故

∠1=∠2.

又∠4=∠2，从而∠1=∠4,即

∠ACB=∠HCG，

因此

AB=HG.

由∠1=∠AGH，知∠2=∠AGH.在△ABE与△GHF中，

∠BEA=∠GFH，∠2=∠AGH，AB=HG,

于是

△ABE≌△GHF，

从而

AE=GF,

故

EG=AF.

综上所述，性质3得证.

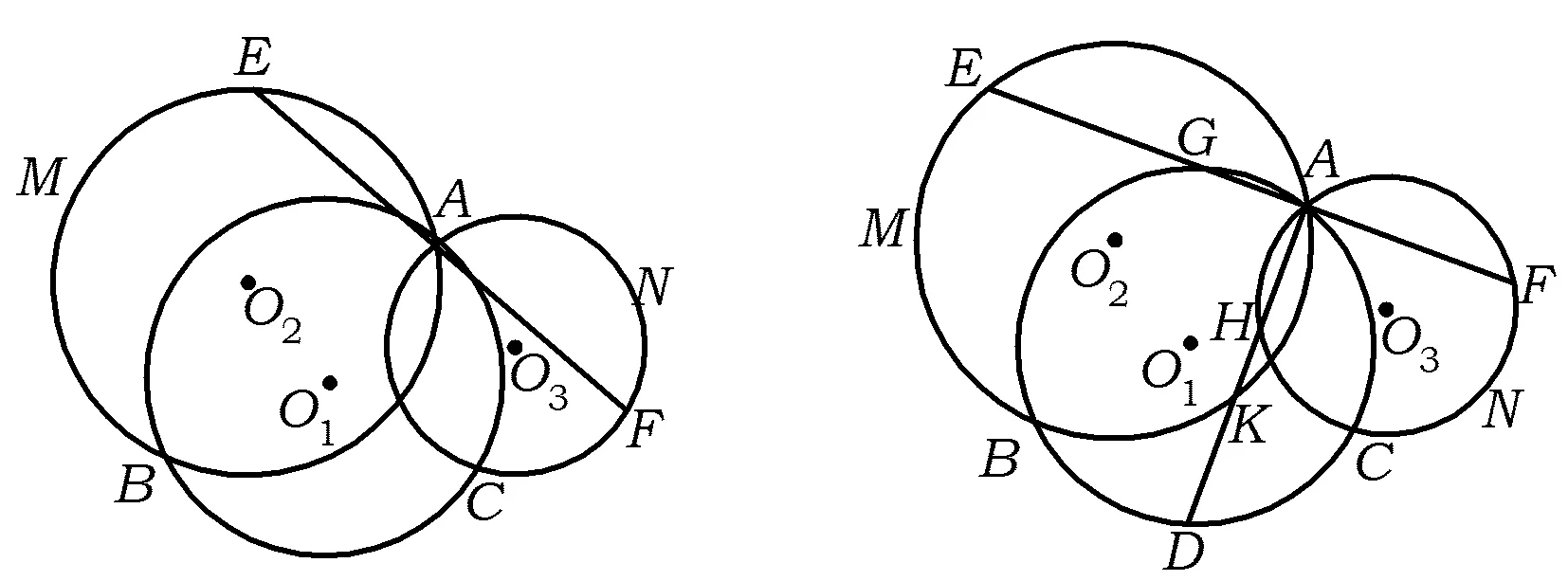
图9　　　　　　　　　图10

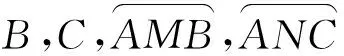
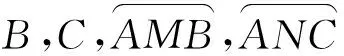
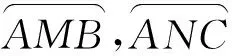
限于篇幅，这里我们把性质4和性质5的证明省略.

美丽图形背后往往隐藏着诸多漂亮的数学结论.有关“等弧度三圆共点图”肯定还有其他有趣的结论，读者可以继续去探究去发现.

[1]李良银.关于三角形中三圆共点问题的探讨[J].宿州教育学院学报,2005,8(4):94-95.

[2]黄新民，刘臻.一道数学中考题的变式与探究[J].中学教研(数学),2015(10)：46-47.

[3]黄新民.简谈整点多边形的存在性问题[J].中学教研(数学),2012(3):4-5.

*收文日期：2016-04-17；2016-05-20

黄新民(1957-)男，浙江温州人，浙江省特级教师.研究方向：数学教育.

O123.1

A

1003-6407(2016)08-27-03