模型分块逼近的RBF网络机械臂自适应控制

姜　静，代　迎，李宏达

(沈阳理工大学 信息科学与工程学院，沈阳 110159)



模型分块逼近的RBF网络机械臂自适应控制

姜静，代迎，李宏达

(沈阳理工大学 信息科学与工程学院，沈阳 110159)

针对隧道掘进后期维护中喷涂机械臂的控制轨迹精确度不高的问题，研究了一类基于模型分块逼近的机械臂RBF网络自适应控制方法。通过RBF网络分别逼近机械臂动力学中的三个方程系数矩阵，设计自适应律，实现机械臂控制，并对系统的稳定性进行证明。仿真显示模型分块逼近的RBF网络自适应方法具有很好的轨迹跟踪特性。

模型分块逼近；机械臂；神经网络；自适应

机械臂是一个复杂的多输入多输出的非线性系统，具有时变，强耦合和高度的非线性的动力学特性。由于测量和建模的不确定性，负载变化及摩擦力等干扰的影响，精确控制十分复杂[1-3]。

RBF神经网络(Radial Basis Function Neural Network)具有良好的泛化能力，网络结构简单。在系统具有较大不确定时，能够有效地提高控制器的性能，神经网络的自适应律可由Lyapunnov方法导出，通过自适应权重的调节保证整个闭环系统的稳定性和收敛性[4]。

本文通过RBF网络分别逼近机械臂动力学中的三个方程系数矩阵，设计自适应律，实现机械臂控制，并对系统的稳定性进行证明。最后仿真显示模型分块逼近的RBF网络自适应方法具有很好的轨迹跟踪特性，并且系统稳定。

1　问题描述

机械臂的控制框图如图1所示。

图1　机械臂控制框图

其中：qd为关节轨迹规划给出的理想轨迹；q为关节实际的位置；e为误差； τ为对于每个关节的控制力矩。

设n关节的机械臂动力学方程为

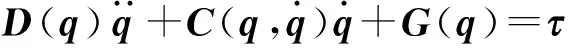
(1)

D(q)=DSNN(q)+ED

(2)

(3)

G(q)=GSNN(q)+EG

(4)

(5)

2　控制律的设计

定义

e(t)=qd(t)-q(t)

(6)

(7)

(8)

式中qd(t)为理想位置的指令,q(t)为实际的位置。

定义

(9)

则有

(10)

(11)

对神经网络的建模项估计如下

(12)

(13)

(14)

将式(7)、(8)带入式(1)中，可得

(15)

控制律设计为

τ=τm+Kpr+KI∫rdt+τr

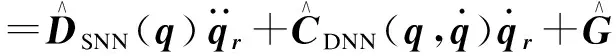
Kpr+KI∫rdt+τr

(16)

式中,KP>0,KI>0。

基于模型的估计控制律为

(17)

用于客服神经网络的建模误差的鲁棒项为

τr=Krsgn(r)

(18)

Kr=diag[krii],krii≥|Ei|

(19)

由上述可得下式

(20)

故而可得

(21)

自适应律设计为

(22)

(23)

(24)

3　稳定性分析

由Lyapunov稳定性定理[5]，Lyapunov函数为

(25)

式中ΓDK、ΓCK和ΓGK为正定矩阵；

(26)

(27)

(28)

(29)

(30)

式(20)带入以上，可得

(31)

由于

(32)

则

(33)

同理可得其他，代入自适应律，可得

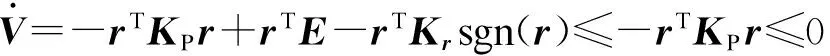
4　仿真实验

选二关节机械臂[7]，不考虑摩擦力和干扰，其动力学模型为：

式中

p=[2.900.760.873.040.87]T

qd1=0.5sin(πt)

qd2=sin(πt)

仿真结果如图2～图8所示。

图2　关节1的轨迹追踪

从图2中，可以看出关节1有良好的跟踪特性，误差为0.085rad。图3中显示了关节1的控制力矩变化，力矩变化平稳，在0.5时进入稳定期。

图3　关节1的控制力矩变化

图4　关节2的轨迹追踪

图5　关节2的控制力矩变化

从图4中，可以看出关节2和关节1一样有良好的跟踪特性，误差为0.082rad。图5中显示了关节2的控制力矩变化，在0.45s时进入稳定期。力矩变化比关节1力矩变化更为平稳，控制性能更佳。

通过矩阵的范数来比较系数矩阵和逼近矩阵的误差，因为高阶矩阵变化很难通过图表显示。从图6、7、8中可以看出神经网络逼近的矩阵变化。

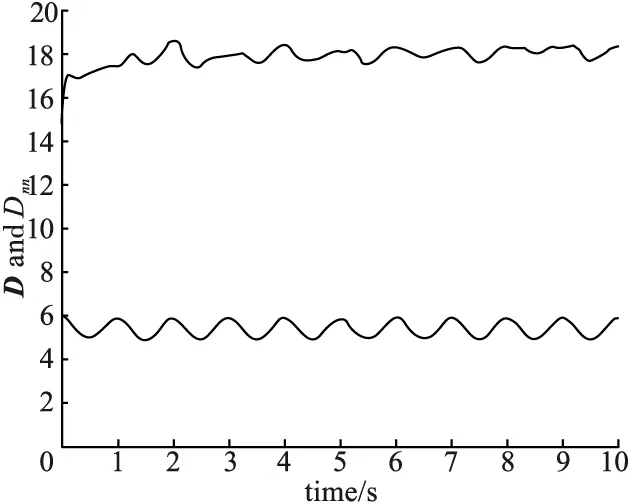
图6　系数矩阵D和Dnn

图7　系数矩阵C和Cnn

图8　系数矩阵G和Gnn

5　结束语

仿真实验使用RBF神经网络对系统进行了基于模型分块逼近的自适应控制。从仿真结果看，由于神经网络的自适应的变化，对于系数矩阵的逼近波动较大,但是系统能够很好地跟踪给出的轨迹，并且控制力矩的变化平稳。能够满足隧道掘进后期维护中，喷涂机械臂的控制精度要求。

[1]Haitao Liu,Tie Zhang.Adaptive Neural Network Finite-Time Control for Uncertain Robotic Manipulators[J].Journal of intelligent & robotic systems:Theory & applications,2014,75(3):367-377.

[2]C Canudas de Wit,B Sicilian,G Bastin.Theory of Robot Control[M].Springer,1996.

[3]Corke P I.Robotics Toolbox(release5)[M].Australia:CSIRO,1999.

[4]Ramirez J R,Cervantes I,Kelly R.PID regulation of robot manipulators:stability and performance[J].Systems & Control Letters，2000(41):73-83.

[5]刘金琨.RBF神经网络自适应控制MATLAB仿真[M].北京 :清华大学出版社,2014.

[6]刘金琨.机器人控制系统的设计与 Matlab 仿真[M].北京 :清华大学出版社,2008.

[7]曹建福.嵌入式柔性开放式数控系统的研究[J].自动化博览,2010(10):5-10.

(责任编辑：马金发)

Adaptive RBF Neural Network Model Block Approach Control of Robotic Manipulators

JIANG Jing，DAI Ying，LI Hongda

(Shenyang Ligong University,Shenyang 110159,China)

To the problem of spray lacquer manipulator trajectory tracking accuracy in latest stage of tunnel excavation,a solution is put forward by model block of the approaching RBF neural network adaptive control method.By approaching of RBF network to three of the mechanical arm dynamics equation coefficient matrix,an adaptive law is designed to control the mechanical arm,which proves system stability.Simulation results show that model block of the approaching RBF network adaptive trajectory tracking control method has very good properties.

model block approximation；robotic manipulators；neural network；adaptive

2015-05-18

国家自然科学基金资助项目(51207096);爆炸科学与技术国家重点实验室(北京理工大学)开放基金资助项目(KFJJ13-6M);

姜静(1973—)，女，副教授，博士，研究方向：复杂系统的建模、优化、控制及仿真。

TP29

A

沈阳理工大学重点学科开放基金资助项目