2D-EIT和3D-EIT仿真结果比较

周旭胜（铜陵学院电气工程学院，安徽铜陵244061）

ZHOU Xu-sheng（School of Electrical Engineering，Tongling University，Tongling，Anhui 244061，China）



2D-EIT和3D-EIT仿真结果比较

周旭胜
（铜陵学院电气工程学院，安徽铜陵244061）

电阻抗断层成像（Electrical Impedance Tomography，简称EIT）的原理是给人体施加微小的电流（电压），在电极上获得相应的测量电压（电流），从而根据一定的算法来实现电导率的重构.因电流在体内的传播是三维的、立体的，所以在研究二维EIT的基础上，通过仿真实验来验证三维EIT的可行性.仿真结果表明：相比2D-EIT，3D-EIT技术可以获得更为丰富的阻抗信息，重构出的图像分布更为接近真实情况.

成像；重构；3D-EIT

1概述

1.1 EIT技术

生物电阻抗断层成像（Electrical Impedance Tomography，EIT）技术是一种新兴的功能成像技术.它的原理是在生物体表设置一定数量的电极，选定其中两个施加微弱电流后，通过测量其他电极上的电压来计算出生物体内电导率的分布［1］.模型图如图1所示：

图1　 EIT电流注入与电压测量和场域示意图

EIT有着其他医学成像技术无法比拟的优点，主要体现在：

1）成像过程中没有使用核素和射线，对人体无害，可以多次重复测量来获取最佳成像效果.

2）功能性成像，成像速度快.

3）系统成本低，携带方便，且不要求特殊的工作环境.

因此，该技术有着非常诱人的应用前景.目前的临床研究主要集中在肠胃与食管功能成像、肺功能成像、脑部功能成像和心脏功能成像等方面［2］.

1.2发展历程

EIT技术早在上世纪20年代就有所涉及，当时有地质学家给地层注入电流，通过观察不同地层的阻抗特性不同，来确定地下矿藏的分布情况.但直至1976年才由美国学家Swanson首次提出电阻抗成像的原理；1982年，英国Sheffield大学Brown和Barber首次获得了阻抗成像，并在1983年公开了他们构建的16电极EIT系统，并给出了成像结果.1995年，希腊Demokritos大学C.S.Koukourlis和Thessaloniki大学的J.N.Sahalos做出了一个32电极数据采集系统；此后，国内也出现了许多EIT研究小组和机构，尤其是第四军医大学及中国医学科学院等著名大学，对EIT的发展起到了很大的推动作用［3-5］.

2 EIT成像过程

2.1硬件系统

EIT硬件系统的主要功能包括：电流的注入、电压的采集和处理以及图像的生成，其原理框图如下图2所示.

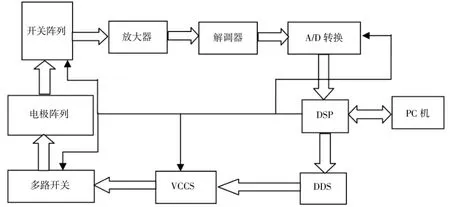
图2　 EIT硬件系统原理图

系统工作时，首先由数字电子合成技术（DDS）在DSP的控制下获得正弦信号，经压控电流源（VCCS）转化成幅度稳定的电流.然后由开关阵列选择电流输入到指定电极，同时测量其它电极上的电压.最后将采集到的数据经过解调、放大和A/D转换，再输入到DSP进行预处理，由计算机完成图像的重构［2］.

2.2 EIT软件实现

EIT软件实现过程主要包括两个方面，正问题求解和逆问题研究［6］.前者的实质是电磁场边值问题的求解，即根据已知电导率求出边界电压；后者是前者的逆过程，即根据边界电压求出电导率分布情况，完成图像的重构.

2.2.1正问题

EIT正问题求解主要有解析法和数值计算法两大类.前者适用于均匀固定的场域，后者则可用于对非均匀场域的求解，因EIT正问题研究的场域是未知的，不均匀的，所以常用数值计算法来进行求解［2］.有限元方法求解正问题是从Laplace方程

▽·（σ▽φ）=0，

出发，在对对象场域进行单元剖分的基础上，对其进行变分和单元插值，进而得到有限元方程

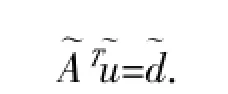
因此，若施加边界条件，即可计算出场域中各点电势.

2.2.2逆问题

EIT逆问题是指以测量电压为基础，通过各种算法得到电导率分布的过程.该过程具有不适定性，也即建立的方程没有真正意义上的解，因此，不能通过一般解方程的方法来求解，只能通过设置一些初始值来进行多次迭代，寻求最佳近似解.这种得到近似解的方法通常称为正则化技术，其过程为：

首先建立最小化泛函

然后运用合适的迭代公式，如牛顿—拉夫逊迭代算法公式

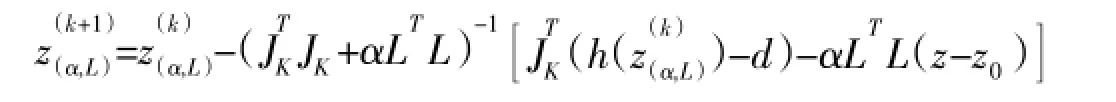
来找到电阻抗z的最优解.

2.2.3仿真实验

本次实验是以MATLAB软件作为平台编程实现的，因该软件中不同的数字可以表示不同的颜色，所以以下的电阻和电导率等参数没设单位，仅用不同大小的数字就足以区分开来.

设置场域为一圆域，半径为14，场域的初始电导率为0.025，有限元剖分节点数为279，单元数为1049，如下图3所示.

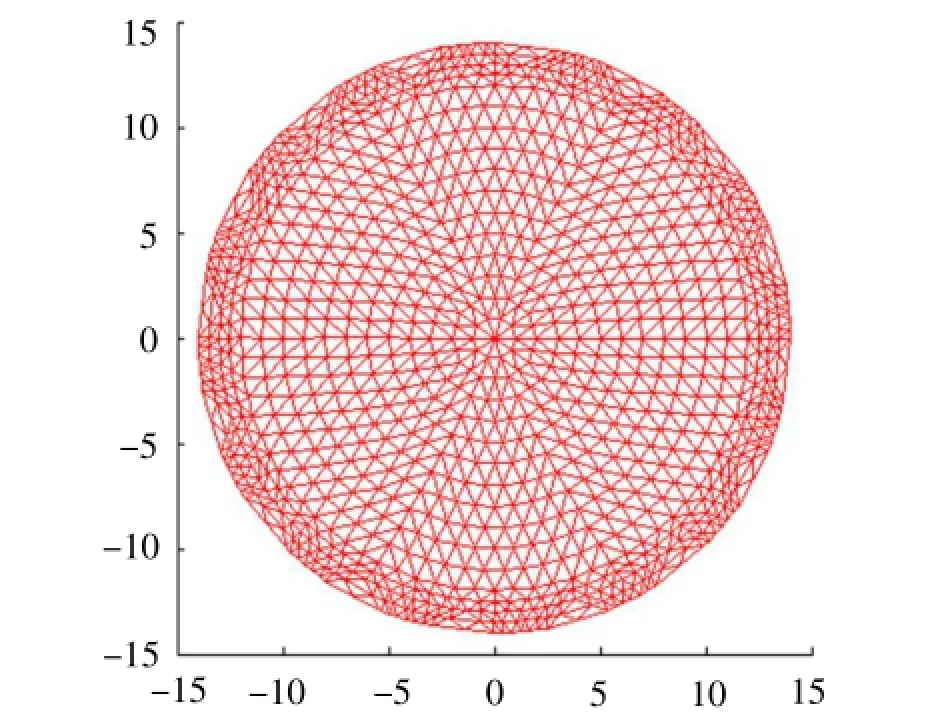
图3　场域模型

在圆域下方设置成像目标，电导率为0.5，如图4所示.运用牛顿-拉夫逊算法对其进行图像重构，结果如下图5所示.

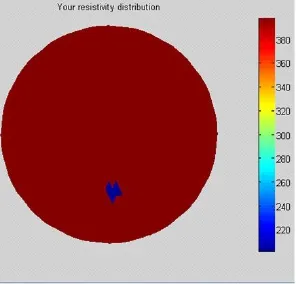
图4　电导率为0.5的成像目标

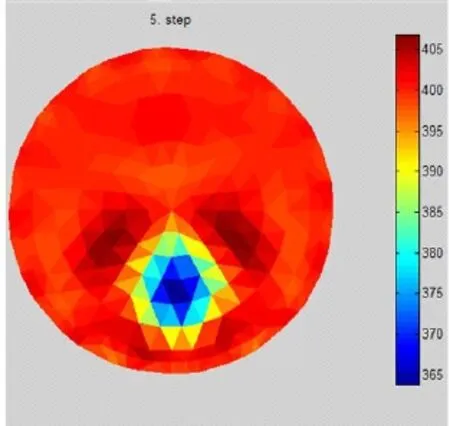
图5　图像重构结果

可见，通过一定的算法，得到的重构图像能够很清楚的反映场域模型中电导率的分布.

3三维EIT

目前，国内外研究小组对2D-EIT技术的研究已趋于成熟，研究成果很多，但由于注入的电流在人体内部并不是以平面方式扩散，而是立体传播，2D-EIT仅能获取的阻抗的平面信息，因此，为获取更为丰富的电阻抗信息，3D-EIT技术的研究就显得日益重要［6］.

相比二维EIT而言，3D-EIT技术的优点主要体现在两个方面：获取的阻抗信息更为丰富和测量系统更接近模型［7］.

三维EIT的实现过程和原理基本与二维EIT相同，分为正问题求解和逆问题研究两个过程.

3.1正问题

正问题研究的关键是场域的数学模型分析.3D-EIT的数学模型种类很多，如连续模型CM（Continuous Model）、间隙模型GP（Gap Model）、分流模型SM（Shunting Model）和全电极模型CEM（Complete Electrode Model），其中，全电极模型被认为是最合理、最为贴近真实情况的模型［8］.

全电极模型的特点是考虑了电极与场域间的接触阻抗.因此，每个电极上的电势为

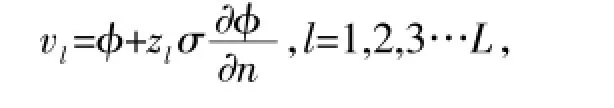
3.2逆问题

逆问题研究的实质是重构出电导率的分布，与二维EIT相似，3D-EIT的图像重构算法一般也是基于正则化技术来实现的.

首先构建目标函数：

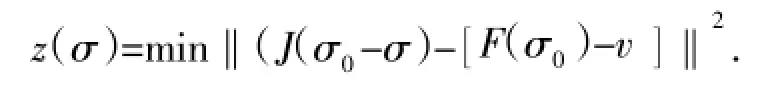
然后通过迭代重构算法，找出使z（σ）最小时对应的σ值就是所要求的最佳解.

3.3仿真实验

本次实验假设场域为一四面体联通的圆柱体模型，有限元剖分结果为376个三角形，共252个节点，模型周围有两层共32个电极.设置场域的原始电导率为1.25，成像目标的电导率为25，电极与场域的基础阻抗为50，分别如图6、图7、图8所示.

图6　圆柱体模型

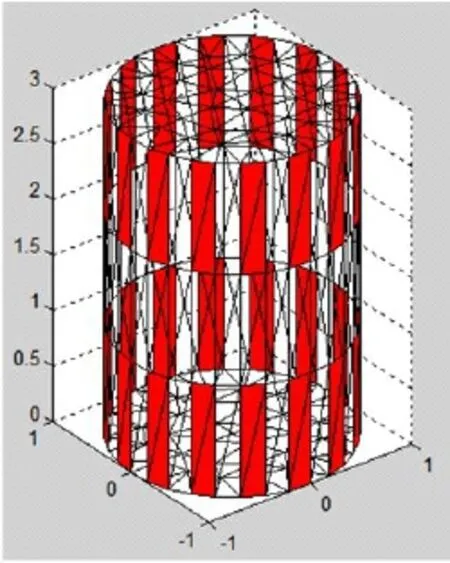
图7　电极模型

图8　成像目标

选用一定的算法对其进行图像重构，得到重构结果如图9所示.

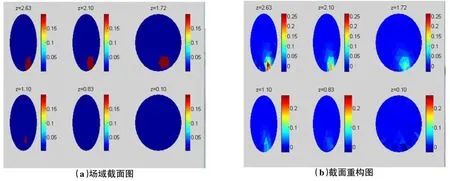
图9　图像重构

图9中，（a）图为圆域模型的6个界面图，选取的位置分别为z=2.63，z=2.10，z=1.72，z=1.10，z=0.83，z=0.10；（b）图为目标图像的重构图像.

对比图5和图9可以看出，无论是2D-EIT还是3D-EIT，其成像结果均能够清楚的反映场域模型中电导率的分布情况，但不同的是，3D-EIT可以获得多个截面的电导率信息，这就相当于是对2D-EIT进行了多次测量.因此，3D-EIT成像结果所包含的信息量要丰富很多，比后者要更为接近真实的显现电导率分布情况，可见在临床实践中，对3D-EIT的研究具有非常的现实意义和应用前景.

［1］任超世，邓娟，王姘.电阻抗断层成像应用技术研究［J］.中国医疗器械杂志，2007，31（4）：1-4.

［2］周舟，胡晓明.EIT技术的研究进展［J］.计算机与信息技术，2010，143（10）：95-96.

［3］周旭胜.基于matlab的EIT图像重构算法研究［D］.南京：南京理工大学，2010.

［4］BARBERD.C，BROWNB.H.Applied Potential Tomography［J］.Phy.Eand Sci.Instru，1984，（17）：723-733.

［5］王妍，任超世.3D-EIT图像重建的研究进展［J］.国外医学生物医学工程分册，2003，26（6）：265-268.

［6］王戬.电阻抗成像算法的研究［D］.济南：山东大学，2006.

［7］DAVIDMS，DOUGLASLM，THOMASEH.Three-DimensionalMillimeter-wave Imaging forConcealedWeaponDetection［J］.IEEE TransMicrowaveTheory Tech，2001，（49）：1581-1592.

［8］黄薏宸.三维电阻抗成像模型与算法研究［D］.重庆：重庆大学，2013.

（责任编辑李健飞）

A Com parative Study of 2D-EIT and 3D-EIT in Sim ulation Results

The principle of Electrical Impedance Tomography is to obtain the corresponding measurement voltages（currents）on the electrode through injecting a small current（voltage）of biomedical tissues，and thus to achieve the electrical conductivity reconstruction of it.Because the transmission path of current in the body is three-dimensional，this paper，based on the research of the 2D-EIT，tests and verifies the feasibility of three-dimensional EIT.The result of simulation shows that，compared to 2D-EIT，more information of the biomedical tissues can be obtained in 3D-EIT，and the reconstructed image distribution is more close to the real situation，

image；reconstruction；3D-EIT

ZHOU Xu-sheng
（School of Electrical Engineering，Tongling University，Tongling，Anhui 244061，China）

TM727

A

1673-1972（2016）03-0032-06

2016-01-20

周旭胜（1986-），男，安徽枞阳人，助教，主要从事电阻抗断层成像研究.