推进轴系—船体结构低频弯曲振动耦合特性

李增光

中国舰船研究设计中心，上海201108

推进轴系—船体结构低频弯曲振动耦合特性

李增光

中国舰船研究设计中心，上海201108

为分析水面舰船推进轴系与船体结构的低频弯曲耦合振动问题，利用有限元法建立了推进轴系—船体结构耦合系统的数学模型，计算系统的垂向及水平向弯曲振动固有特性，并与利用简化模型得到的计算结果进行了对比分析。结果表明：在推进轴系第1阶弯曲振动固有频率以下频段，推进轴系—船体结构系统主要体现为船体梁振动，推进轴系跟随船体梁运动；在推进轴系的每阶振动固有频率附近，由于存在一个固有频率非常接近的船体梁振动模态，故在该频段桨—轴系统与船体梁有较强的耦合作用；在船体梁的质量及截面面积惯性矩远大于轴系对应参数的情况下，仅分析推进轴系自身的低频固有振动特性时，将船体结构简化为刚性安装基础所带来的误差很小，但是推进轴系简化模型不能反映推进轴系—船体结构的耦合振动模态及多轴系时的反相位振动模态。

推进轴系；船体结构；耦合振动；有限元；数值仿真

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.tj.20160531.1104.026.html期刊网址：www.ship-research.com

引用格式：李增光.推进轴系—船体结构低频弯曲振动耦合特性［J］.中国舰船研究，2016，11（3）：74-78.

LI Zengguang.The bending vibration characteristic of a propulsion shafting and hull structure coupled system at low frequencies［J］.Chinese Journal of Ship Research，2016，11（3）：74-78.

0　引　言

在船舶设计过程中，对推进轴系的低频振动特性及船体结构总振动进行计算和评估是总体设计的关键问题之一。通常借助仿真手段对推进轴系的纵向［1］、扭转［2］、横向（回旋）振动［3］以及船体总振动［4-5］进行计算，并分析其低阶固有频率与船舶的主要激励频率是否有足够的避开裕度。目前，在工程设计中往往将推进轴系和船体结构作为独立的研究对象，分别对其进行计算分析，不考虑两者之间的耦合作用。实际上，推进轴系通过其支承轴承与船体结构连为一体；在低频段，推进轴系弯曲振动与船体梁弯曲总振动的固有频率处于同一数量级，两者之间应具有较强的耦合作用。

近年来，从舰艇减振降噪、大型民用船舶推进轴系状态检测等角度出发，各研究机构对螺旋桨—推进轴系与船体结构的耦合振动问题开展了研究，重点分析了声频段内（数十赫兹以上）的振动传递、声辐射与控制技术［6-12］，以及准静态频段内的船体变形对轴系对中状态的影响［13-15］等问题。然而，对次声频段内（20 Hz以下）船体梁与推进轴系（含螺旋桨和轴）的弯曲振动的耦合特性研究较少。

对采用长轴系的单体水面舰船而言，推进轴系和船体结构的低阶弯曲振动固有频率主要处于次声频段。水面舰船推进轴系转速范围内的车令设置较多，各车令对应的轴频、螺旋桨叶频及其倍频较为密集，且亦基本处于次声频段。因此，使推进轴系、船体结构弯曲振动的低阶固有频率与主要激励频率均有足够大的避开裕度，难度较大，需要提高设计中固有特性计算分析的准确性。理论上讲，将推进轴系与船体结构作为一个整体系统进行分析，可提高系统低频固有特性计算的准确性。因此，本文将以某小型水面船的推进轴系—船体结构为研究对象，通过数值计算分析其低频弯曲振动的耦合特性及工程简化计算方法的可靠性，以期为工程设计提供参考。

1　计算模型及参数

水面舰船的桨—轴系统通过若干支承轴承连接（图1）。舰船单个舱段的底部、舷侧等结构的首阶弯曲振动固有频率通常在20 Hz以上，因此在20 Hz以下的低频段，整个船体结构可近似为梁模型。由于船体梁的长高之比较小，故采用计入截面剪切变形及转动惯量影响的Timoshenko梁模型［16］。水面舰船推进轴系的长度与直径之比较大，故轴系采用Euler梁模型模拟。由于支承轴承的质量远小于轴系及船体结构的质量，因此可将支承轴承简化为不计质量的弹簧模型。螺旋桨采用考虑转动惯量的集中质量模型。本文主要研究推进轴系—船体结构系统的垂向及水平向的弯曲振动特性，模型中不考虑船体梁的弯扭耦合振动效应。采用有限元法建立该耦合系统动力学分析模型，如图1（b）所示。

图1　水面舰船推进轴系—船体结构耦合系统Fig.1　Propulsion shafting-hull coupled system of a surface warship

利用有限元法，建立桨—轴—船系统低频弯曲振动的自由运动微分方程

式中：M，K分别为系统的质量和刚度矩阵；U为位移向量。求解方程（1）的特征值可得到固有频率及其振型。

某型船水线长约80 m，机舱位于中部，双轴双桨；推进轴系长约30 m，轴段的内外径分别约为0.13和0.3 m，通过6个径向支承轴承安装于船体结构上，其垂向刚度分别取5.6×108，7.6×108，2.2×108，1.0×109，1.0×109，1.0×109N/m；水平向刚度分别为 4.5×108，1.3×108，2.2×108，1.0×109，1.0×109，1.0×109N/m；螺旋桨位于船艉端向前约5 m处。左右舷轴系对称布置，分别简化为一个等效梁模型，通过其支承轴承与船体结构连接。根据本船20站质量分布（计入附连水质量）及截面几何参数，将船体结构简化为由20段等截面匀质梁段组成的变截面Timoshenko梁。每段等截面匀质梁大致分为4个Timoshenko梁单元；若该段梁内有支承轴承，则在轴承位置处设置一个节点。根据轴系截面直径变化及支承轴承位置，将其分成若干段等截面梁，每段梁分成若干Euler梁单元。可见，此双轴系水面船的推进轴系—船体结构耦合系统的低频弯曲振动分析模型包含2个模拟桨—轴系统的Euler梁模型，以及1个模拟船体结构的Timoshenko梁模型，即三梁耦合模型。

在单体船舶的总振动计算中，通常利用船体梁模型分析整船的低频振动固有频率，而将桨—轴系统按其质量分布计入船体梁的相应站位。可见，船体梁模型近似于三梁耦合模型中支承轴承刚度取无穷大的情况。在推进轴系振动特性计算中，通常假设桨—轴系统由支承轴承固定于刚性基础上，即认为船体结构为刚性基础。这种推进轴系简化模型近似于三梁耦合模型中船体梁的刚度无限大，且其平动自由度被约束的情况。然而，实际的船体梁为弹性体，且首阶固有频率仅数赫兹。为分析船体梁与桨—轴系统的耦合特性以及简化模型的可靠性，下面利用三梁耦合模型及简化的船体梁模型和推进轴系模型分别计算推进轴系—船体结构系统及子系统的弯曲振动固有特性，根据仿真计算结果开展对比分析。

2　垂向固有振动特性

利用三梁耦合模型、简化的船体梁模型和推进轴系模型分别计算推进轴系—船体结构耦合系统、船体结构和桨—轴系统的垂向弯曲振动固有频率，其结果如表1所示，典型振型如图2所示。

表1　不同模型垂向固有频率计算结果Tab.1　Simulation results of vertical bending natural frequency using different models

由表1及图2可见，在低于推进轴系第1阶固有频率（10.11 Hz）的频段，轴系—船体梁耦合系统主要表现为船体梁的振动，推进轴系跟随船体梁运动（图2（a）），故该频段应注意船体动态变形对推进轴系校中状态的影响。在推进轴系相邻两阶固有频率之间的频段，存在若干船体梁与轴系梁的耦合振动模态（图2（e）），但由于本船桨—轴系统的单位长度质量、截面面积惯性矩比船体梁对应参数分别小2和4个数量级，故桨—轴系统对船体梁固有振动特性的影响非常小。还可看出，在推进轴系的每阶振动固有频率附近，均存在1个固有频率接近的船体梁振动模态（图2（b）），在该频段附近桨—轴系统的激励可能会引起较强的船体结构总振动响应。

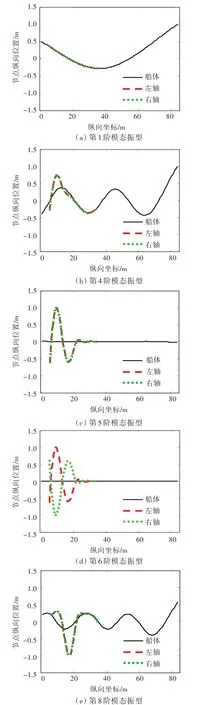
图2　耦合系统典型垂向弯曲振动模态Fig.2　Typical modes of bending vibration in vertical direction

对应简化推进轴系模型的每阶固有频率，三梁耦合模型均存在频率非常接近的2个模态，左、右2根轴系分别表现为同相位振动（图2（c））和反相位振动（图2（d））。

从表1中三梁耦合模型及推进轴系简化模型的结果可见，由于船体梁的单位长度质量及截面弯曲刚度均远大于轴系相应参数，故在此情况下是否考虑推进轴系安装基础（船体结构）的弹性，对推进轴系自身低阶模态固有频率的计算结果影响很小。但是，三梁耦合模型能反映推进轴系—船体梁的耦合振动模态以及两轴系的反相位振动模态。

对应简化推进轴系模型的每阶固有频率，三梁耦合模型存在1个包含3阶模态的模态簇（表1中黑体标记数据），其中2阶模态主要表现为桨—轴系统振动，另一阶模态表现为桨—轴系统与船体结构的耦合振动。

3　水平向固有振动特性

利用三梁耦合模型、简化的船体梁模型和推进轴系模型分别计算推进轴系—船体结构耦合系统、船体结构和桨—轴系统的水平向弯曲振动固有频率，其结果如表2所示，典型振型如图3所示。

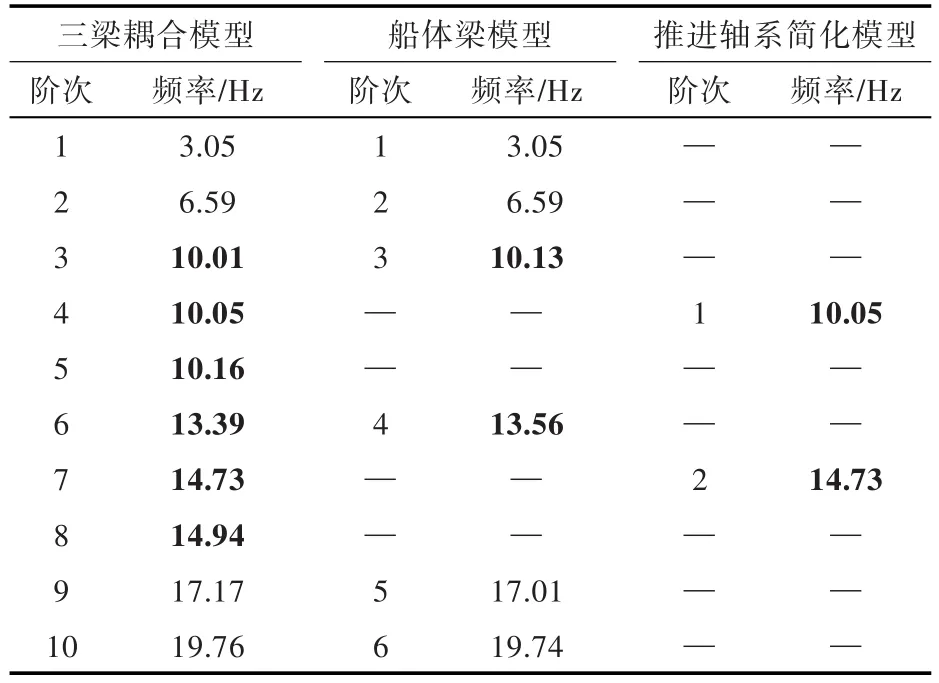
表2　不同模型水平向固有频率计算结果Tab.2　Simulation results of horizontal bending natural frequency using different models

由表2及图3可见，推进轴系—船体结构耦合系统的水平向振动固有特性呈现出与垂向振动类似的特征，存在模态簇及强耦合振动模态。由表2可见，对应简化推进轴系模型的第2阶模态，三梁耦合模型存在1个包含3阶模态的模态簇（表2中用黑体标记数据），这3阶模态的固有频率分别为13.39，14.73和14.94 Hz，频带宽度约为简化推进轴系模型的第2阶模态固有频率的11%。若根据简化模型的固有频率计算结果，通过车令优化使避开裕度达到10%，可能达不到预期目标。因此，工程设计中应关注该问题。

图3　耦合系统典型水平向弯曲振动模态Fig.3　Typical modes of bending vibration in horizontal direction

4　结　论

利用有限元法建立了用于分析水面舰船推进轴系—船体结构耦合系统的低频弯曲振动特性的数学模型，通过系统固有特性的数值计算，研究了推进轴系与船体结构低频弯曲振动的耦合特性。数值计算结果表明：

1）在推进轴系第1阶弯曲振动固有频率以下频段，推进轴系—船体结构系统主要体现为船体梁振动，推进轴系跟随船体梁运动，需要注意船体梁动态变形对推进轴系校中状态的影响。

2）在推进轴系的每阶振动固有频率附近，均存在1个固有频率接近的船体梁振动模态，在该频段内桨—轴系统的激励将引起较强的船体振动。

3）在船体结构单位长度质量及截面面积惯性矩均远大于推进轴系对应参数的情况下，仅分析推进轴系自身的低频固有振动特性时，安装基础的弹性对计算结果影响很小；但是采用推进轴系简化模型将不能反映推进轴系—船体结构的耦合振动模态及多轴系情况下的反相位振动。

［1］ 秦春云，杨志荣，饶柱石，等.船舶推进轴系纵向振动抑制研究［J］.噪声与振动控制，2013，33（3）：147-152.

QIN Chunyun，YANG Zhirong，RAO Zhushi，et al. Study on suppression of the longitudinal vibration of ship's propulsion shafting system［J］.Noise and Vibra⁃tion Control，2013，33（3）：147-152.

［2］沈小寒.大功率复杂推进轴系扭振特性的研究［D］.上海：上海交通大学，2013.

［3］ 刘刚，吴炜，饶春晓，等.基于传递矩阵法的船舶轴系回旋振动计算研究［J］.中国舰船研究，2010，5 （1）：60-63.

LIU Gang，WU Wei，RAO Chunxiao，et al.Numerical calculation of whirling vibration of ship shafts based on transfer matrices method［J］.Chinese Journal of Ship Research，2010，5（1）：60-63.

［4］周平，赵德有.动态刚度阵法在船体总振动计算中的应用［J］.船舶力学，2006，10（4）：126-132.

ZHOU Ping，ZHAO Deyou.Application of dynamic stiffness matrix method to compute the vibration of ship hull［J］.Journal of Ship Mechanics，2006，10（4）：126-132.

［5］ 王显正，赵德有，孙超，等.船舶总振动固有频率实用算法［J］.中国舰船研究，2007，2（1）：56-58.

WANG Xianzheng，ZHAO Deyou，SUN Chao，et al. Improved algorithm for the natural frequencies of ship vibration［J］.ChineseJournal of ShipResearch， 2007，2（1）：56-58.

［6］ 朱理，庞福振，康逢辉.螺旋桨激励力下的舰船振动特性分析［J］.中国造船，2011，52（2）：8-15.

ZHU Li，PANG Fuzhen，KANG Fenghui.Vibration characteristic of a warship subjected to propeller excita⁃tion［J］.Shipbuilding of China，2011，52（2）：8-15.

［7］高菊，陈美霞.偶极子源与力激励作用下截顶锥形壳振动与声辐射研究［J］.中国舰船研究，2011，6 （1）：46-51，55.

GAO Ju，CHEN Meixia.Sound and vibration of a trun⁃cated conical shell under excitation of dipole source and force［J］.Chinese Journal of Ship Research，2011，6（1）：46-51，55.

［8］李栋梁.轴系—艇体耦合系统振动声辐射分析与实验研究［D］.上海：上海交通大学，2012.

［9］ 谢基榕，徐利刚，沈顺根，等.推进器激励船舶振动辐射声计算方法［J］.船舶力学，2011，15（5）：563-569.

XIE Jirong，XU Ligang，SHEN Shungen，et al.Calcu⁃lational method for radiating sound excited by vibration of ship propeller［J］.Journal of Ship Mechanics，2011，15（5）：563-569.

［10］ DYLEJKO P G，KESSISSOGLOU N J，TSO Y，et al. Optimisation of a resonance changer to minimise the vibration transmission in marine vessels［J］.Journal of Sound and Vibration，2007，300（1/2）：101-116.

［11］MERZ S，KINNS R，KESSISSOGLOU N.Structural and acoustic responses of a submarine hull due to pro⁃peller forces［J］.Journal of Sound and Vibration，2009，325（1/2）：266-286.

［12］CARESTA M，KESSISSOGLOU N J.Reduction of hull-radiated noise using vibroacoustic optimization of the propulsion system［J］.Journal of Ship Re⁃search，2011，55（3）：149-162.

［13］MURAWSKI L.Shaft line alignment analysis taking ship construction flexibility and deformations into con⁃sideration［J］.Marine Structures，2005，18（1）：62-84.

［14］严新平，李志雄，袁成清，等.考虑船体变形耦合作用的船舶推进系统建模与控制［J］.船海工程，2011，40（1）：60-63.

YAN Xinping，LI Zhixiong，YUAN Chengqing，et al.Modelling and control of marine propulsion system coupled with hull deformation［J］.Ship and Ocean En⁃gineering，2011，40（1）：60-63.

［15］ 秦丽.大型船舶推进轴系功率流分析理论与方法研究［D］.武汉：武汉理工大学，2014.

［16］ 帕利O M，巴依佐夫Γ B，沃罗涅诺夫E Я.船舶结构力学手册［M］.徐秉汉，徐绚，徐铭麒，译.北京：国防工业出版社，2002.

The bending vibration characteristic of a propulsion shafting and hull structure coupled system at low frequencies

LI Zengguang
Shanghai Division，China Ship Development and Design Center，Shanghai 201108，China

In this paper，a finite element simulation model of the propulsion shafting and hull structure system is developed for analyzing the coupled bending vibration characteristic at low frequencies.The natu⁃ral frequencies and modal shapes are analyzed through numerical simulation and are then compared with those from simplified simulation models.Simulation results show that at frequencies lower than the natural frequency of the first bending vibration mode，the coupled system vibrates under the hull-beam mode，and the shafting follows the hull.Near each natural frequency of the shafting，a vibration mode of hull structure also appears，and，therefore，the propeller-shafting's vibration can be transferred to the hull structure effec⁃tively.If the mass and cross-section area moment of the hull are far larger than those of shafts，and when the vibration modes of propulsion shafting are the only research subjects，the hull structure can be treated as a rigid body with little error.However，the coupled vibration mode and the shafts'anti-phase vibration mode may not be correctly reflected.

propulsion shafting；hull structure；coupled vibration；finite element；numerical simulation

U664.2

A

10.3969/j.issn.1673-3185.2016.03.013

2015-07-30网络出版时间：2016-5-31 11:04

李增光（通信作者），男，1982年生，博士，工程师。研究方向：舰船推进系统设计及振动噪声控制。E-mail：22102106@qq.com