基于突变级数法的舰船作战能力综合评价
谢宗仁,吕建伟,林华
1海军工程大学管理工程系,湖北武汉4300332海军工程大学电子工程学院,湖北武汉430033
基于突变级数法的舰船作战能力综合评价
谢宗仁1,吕建伟1,林华2
1海军工程大学管理工程系,湖北武汉430033
2海军工程大学电子工程学院,湖北武汉430033
为适应现代海军信息化条件下的作战要求,满足遂行多样化军事作战任务的目标,以编队协同作战为背景,在分析突变理论基本思想和算法步骤的基础上,提出一种基于突变级数法的舰船作战能力综合评价方法。根据突变级数理论,对影响舰船协同作战能力的因素进行多层次分解,建立舰船协同作战能力综合指标体系,确定各层次指标突变类型。在对数据进行无量纲化处理之后,结合突变层次结构模型进行综合量化运算,得到最后的评价结果。该方法已应用于某系列舰船作战效能的评估之中,计算结果真实准确,为舰船协同作战能力的评价提供了一种新的思路和方法。
突变级数法;舰船;作战能力;评价
0 引 言
由于现代作战中目标难以探测、跟踪,作战时间非常短促,且来袭目标多采用饱和攻击样式,故采用单一舰载作战系统独立进攻和防御的作战模式已很难有效保护舰艇自身的安全,也无法达到预期的作战效果[1]。因此,为提高舰艇编队的整体作战效能,提高编队内舰艇的生存能力,必须着力开展未来海战中水面舰艇多平台协同作战能力的研究。本文将在深入探讨突变级数法的基础上,重点以海上协同作战为背景,研究舰船协同作战能力体系结构及其指标评价。
1 突变级数法评价的基本原理及其分析
以专家评分法为基础的层次分析法、模糊综合评判法、马尔科夫链和灰色系统等传统评价方法比较依赖调查对象的主观感觉,其评价结果随评价人员主观因素的不同而有着较大的差别,具有较强的不确定性[2-6]。这些评价方法中均涉及到指标权重的获取,在确定权重时常常通过专家评分法或者两两比较的方式确定层次中诸因素的相对重要性,该过程存在较强的主观因素,权重的确定问题难以得到科学、正确的解决。
突变级数法(Catastrophe Progression Method,CPM)是在突变理论的基础上发展起来的一种综合评价方法。该方法考虑了各评价指标的相对重要性,定性分析与定量计算相结合,能减少主观性,又不失科学性、合理性,计算过程简单,计算结果准确[7-10]。此方法多应用于需要进行分类分级分析的研究中。其思想是将所研究系统的评价模型分解为若干个指标,由低层指标向高层指标逐层综合,再把各层的控制变量代入相应的突变模型中进行归一化计算,对于同一评价对象采取“舍大取小”原则或取平均值,得到各层次的突变级数。其具体评价步骤如下。
1.1建立递阶层次结构模型
首先,根据评估目的对评价总体指标进行多层次、分主次分解,排列成递阶目标层次结构,由评价总体指标逐渐分解到最下层子指标。一般只需要掌握最底层指标的原始数据即可。对一个指标进行多层次分解,是为了得到更具体的指标,以便进行量化,当分解到可以计量的子指标时,分解即可停止。
1.2各层次突变系统的分类
可按照突变论创立者——法国数学家Thom提出的分类定理对突变论模型进行分类[11-12]。光滑函数 f:Rn→R的一个r参数族,对于任何有限的n,全部r<5在结构上是稳定的,而且等价于下列形式之一:在非驻点附近,u1;在常态驻点(或Morsc点)附近,(0≤i≤n)。
但这2种形式均不是突变形式,因为它们与参数tj(1<j<r)的变化无关。
而在退化驻点附近的标准形式称为突变,这些突变的名称按照Arnol'd的系统分类符可分为类尖点突变和脐点突变2大类,本文仅讨论类尖点突变,其常见的5种类型如图1所示。图中:①为折叠突变;②为尖点突变;③为燕尾突变;④为蝴蝶突变;⑤为棚屋突变。数学模型分别如下。
折叠突变:f(x)=x3+ax;
尖点突变:f(x)=x4+ax2+bx;
燕尾突变:f(x)=x5+ax3+bx2+cx;
蝴蝶突变:f(x)=x6+ax4+bx3+cx2+dx;
棚屋突变:f(x)=x7+ax5+bx4+cx3+dx2+ex。其中:x为突变系统中的一个状态变量;f(x)为状态变量x的势函数;a,b,c,d和e为状态变量的控制变量。

图1 常见的突变模型示意图Fig.1 Diagrams of common catastrophe model
1.3由突变系统的分歧方程导出归一公式
突变系统的势函数为 f(x),根据突变理论,将其所有临界点集合成平衡曲面,方程通过对f(x)求一阶导数,即 f′(x)=0而得。其奇点集通过对 f(x)求二阶导数而得,即通过 f″(x)=0消去x,得到突变系统的分歧点集方程。分歧点集方程表明,当诸控制变量满足此方程时,系统就会发生突变[5-6]。通过分解形式的分歧点集方程导出归一公式,由归一公式将系统内诸控制变量不同的质态化为同一质态,即化为由状态变量表示的质态。
各类型突变系统的分歧点集方程及归一化公式如表1所示。
1.4利用归一公式进行综合评价
利用归一公式对同一控制对象各个控制变量(指标)计算出的x值采用“互补”与“非互补”原则,求取系统的总突变隶属函数值。“互补”原则是指一个系统各控制变量(如a,b,c和d)之间可以互相弥补其不足,以使相应的x值达到较高的平均值,即 x=(xa+xb+xc+xd)/4。“非互补”原则是指一个系统的控制变量之间不可互相弥补其不足,因此,按归一公式求系统状态变量x的值时,要从各控制变量相对应的xa,xb,xc和xd等变量中取最小的一个作为整个系统的x值。同理,经过逐层递阶运算,即可得到总突变隶属函数值。

表1 各突变模型的分歧点集方程及归一化公式Tab.1 Bifurcation set equations and normalization formulas of catastrophe models
2 突变级数法在舰船协同作战能力评估中的应用
舰船协同作战是指在编队对抗条件下,以各舰船作战能力为支撑,充分利用空、岸、天、潜的信息支援,基于协同指挥控制技术,完成对敌打击作战,是现代海军编队的典型作战样式。舰船协同作战的主要特点是:探测节点、指挥节点、武器节点分离,通过通信网络有机结合;信息交互复杂,信息处理分布式实施,指挥决策占有核心作用;态势动态变化,对协同作战效能的影响因素众多,效能评估复杂[13]。因此,为了更科学地对舰船协同作战能力进行评估,相对于其他评价方法,采用减少了主观因素的突变级数法具有很大的优势。
2.1舰船协同作战能力指标体系的建立
建立指标体系时,首先要考虑各层次指标的重要程度。以现代化信息战争条件下航母编队中单艘驱逐舰为背景,将影响舰船协同作战能力的要素主要划分为2大类:协同信息对抗能力和协同火力对抗能力,信息对抗的重要程度大于火力对抗,从而形成一级指标。同时,根据编队作战任务要求,对这2大类能力进行继续分解:将协同信息对抗能力分解为协同通信对抗能力和协同电子对抗能力2个子要素;将协同火力对抗能力分解为协同防空作战能力、协同反潜作战能力、协同反舰作战能力、协同对陆作战能力4个子要素,从而形成6个二级指标,其指标重要性依次减小。
同样,根据舰船各系统在协同作战中不同的作战职能和作战任务,将二级指标进一步细分为23个三级指标,从而形成了舰船协同作战能力评价指标体系,如表2所示。
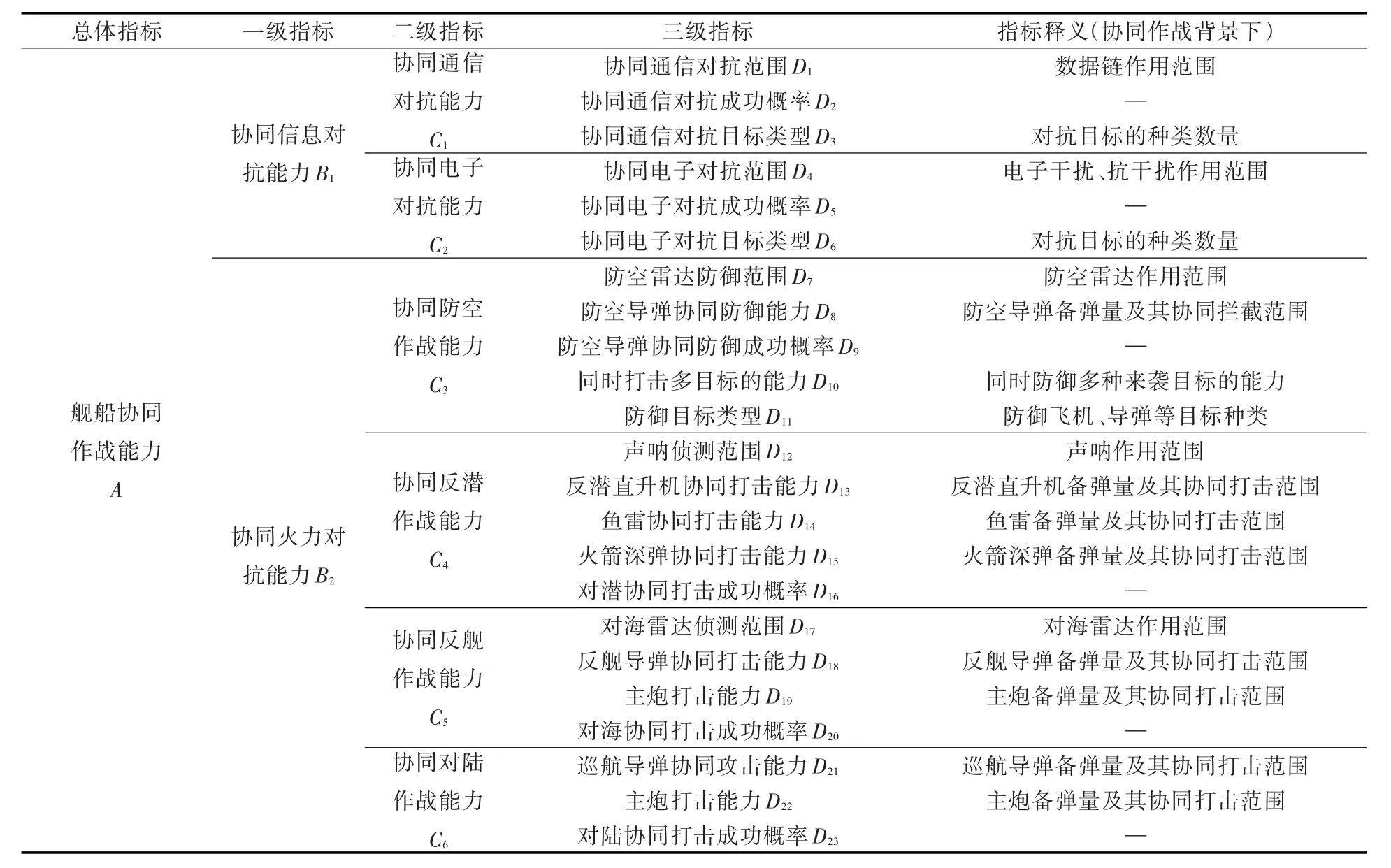
表2 舰船协同作战能力评价指标体系Tab.2 The evaluation indicator system of ship's cooperative engagement capability
2.2确定各层指标的突变系统类型
由突变系统的分类方法可知,表2所建立的指标体系中的各级指标要素构成了2个尖点突变,3个燕尾突变,2个蝴蝶突变,2个棚屋突变。具体突变形式如下:
尖点突变:A→(B1,B2);
B1→(C1,C2)。
燕尾突变:C1→(D1,D2,D3);
C2→(D4,D5,D6);
C6→(D21,D22,D23)。
蝴蝶突变:B2→(C3,C4,C5,C6);
C5→(D17,D18,D19,D20)。
棚屋突变:C3→(D7,D8,D9,D10,D11);
C4→(D12,D13,D14,D15,D16)。
2.3示例计算及结果分析
现对海军某系列共4型(I型、II型、III型、IV型)驱逐舰的协同作战能力进行评价。
2.3.1原始数据的无量纲化处理
通过查阅相关资料以及实际调研数据情况,对不同型驱逐舰的三级指标进行排序(表3)。按照排序对第1~4位(针对每个指标,4型舰排序)分别赋予0.8,0.6,0.4和0.2分。例如,对于I型舰的二级指标C1(协同通信对抗能力)的3个三级指标D1(协同通信对抗范围)、D2(协同通信对抗成功概率)和D3(协同通信对抗目标类型)的排序分别为4,1,3,则其指标对应的得分别为0.2,0.8,0.4。其他三级指标的得分依此类推。
2.3.2二级指标的评价结果
利用归一公式自下向上逐步综合,直到得出最高层总指标的评价结果。以I型驱逐舰为例,根据归一公式,其具体计算方法如下。
1)协同通信对抗能力指标。
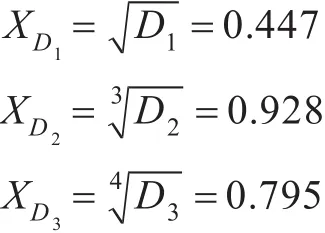
按照“互补”原则,可求得指标均值为XC1=(XD1+XD2+XD3)/3=0.724。
2)协同电子对抗能力指标。
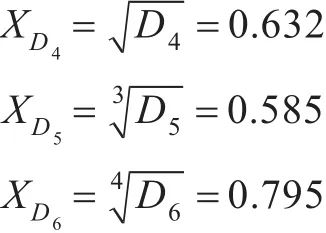
按照“互补”原则,可求得指标均值为
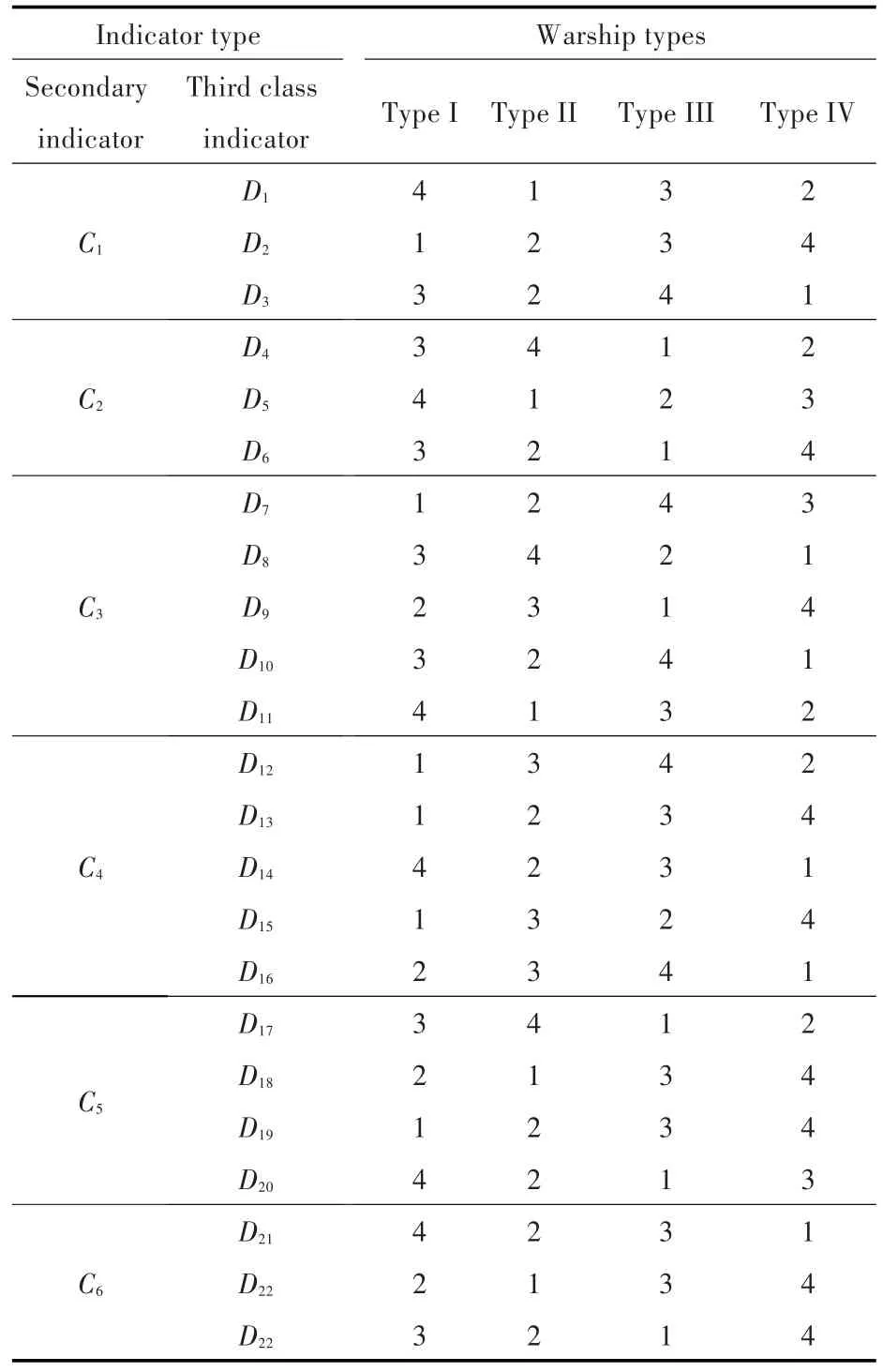
表3 三级指标排序结果Tab.3 Ranking results of the third class indicators
XC2=(XD4+XD5+XD6)/3=0.671。
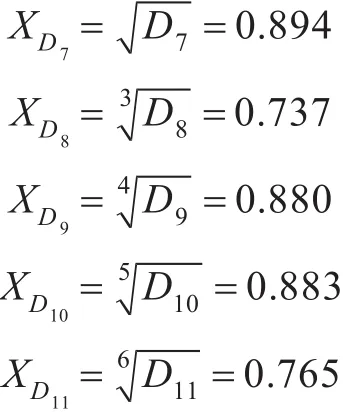
3)协同防空作战能力指标。按照“互补”原则,可求得指标均值为。
4)协同反潜作战能力指标。

5)协同反舰作战能力指标。
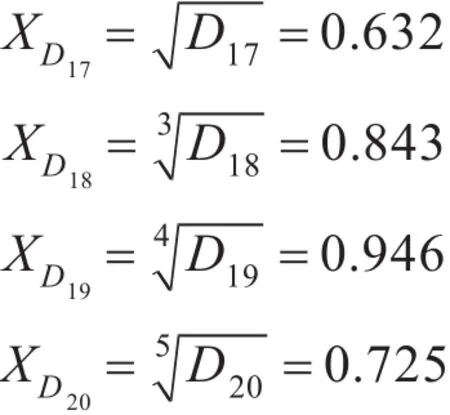
6)协同对陆作战能力指标。
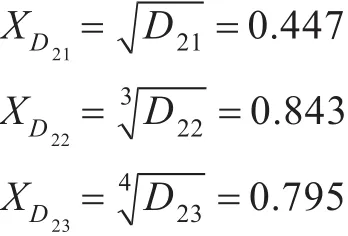
同理,可得到其他3型驱逐舰二级指标的评价值,计算结果如表4所示。
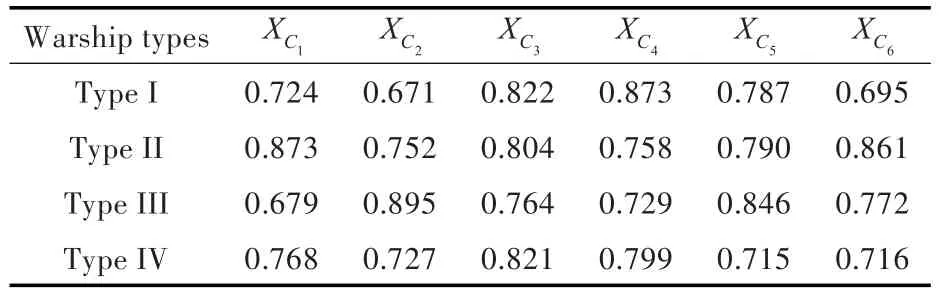
表4 各型舰二级指标评价值Tab.4 The secondary indicators'evaluation results of different warships
2.3.3总体指标综合评价结果
如前分析,构成舰船协同作战能力的2个一级指标形成了尖点突变A→(B1,B2),6个二级指标分别形成了尖点突变B1→(C1,C2)和蝴蝶突变B2→(C3,C4,C5,C6),要对总体指标进行评价,就需要进一步综合二级指标和一级指标。同样,以I型舰为例。
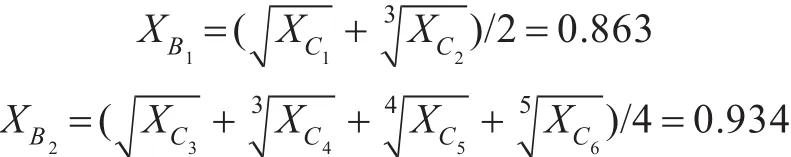
同理,可求得II型、III型和IV型舰的协同作战能力评价值分别为:

由以上分析可见,基于突变级数法的各型舰的协同作战能力评价排序为:II型>III型>IV型>I型。这与各型舰的单舰对抗能力排序相一致,证明计算结果准确、可信。
3 结语
作为一种基于状态分析的动态评价方法,突变级数法既弥补了静态评价方法的不足,减少了权重赋值的主观性,又避免了主观判断的不确定性,因此运用突变级数法评价舰船协同作战能力的主观性较小,评价结果较为准确。示例表明,突变级数法的计算结果是合理、客观而可行的,它为解决舰船协同作战能力的评价问题提供了一种新的思路。
[1]徐圣良,姜青山,单利建.舰机协同作战理论的两栖作战火力协同[J].火力与指挥控制,2012,37 (3):110-115.
XU Shengliang,JIANG Qingshan,SHAN Lijian.Am⁃phibious operation firepower cooperation based on war⁃ship-aircraft cooperation operation theory[J].Fire ControlandCommandControl,2012,37(3):110-115.
[2] 吕建伟,王新磊,曾宏军.海军舰船设计方案的评估方法研究[J].中国舰船研究,2006,1(1):21-24.
LV Jianwei,WANG Xinlei,ZENG Hongjun.Research on the assessment methodology for design alternatives of navy vessels[J].Chinese Journal of Ship Research,2006,1(1):21-24.
[3]陈子凯,林少芬,江小霞.基于马尔可夫过程的船舶电站冗余系统可靠性分析[J].中国造船,2010,51(1):176-182.
CHEN Zikai,LIN Shaofen,JIANG Xiaoxia.Reliabili⁃ty analysis of redundant system in marine power station based on Markov process[J].Shipbuilding of China,2010,51(1):176-182.
[4] CHENG K,ZHANG H J,ZHANG R.A task-resource allocation method based on effectiveness[J].Knowl⁃edge-Based Systems,2013,37:196-202.
[5]刘旸,孟梅,张恒,等.基于MAS和FS的多任务舰船作战效能评估方法[J].哈尔滨工业大学学报,2014,46(2):121-128.
LIU Yang,MENG Mei,ZHANG Heng,et al.Effec⁃tiveness evaluation method of naval ship oriented to multi-mission based on MAS and FS[J].Journal of Harbin Institute of Technology,2014,46(2):121-128.
[6]VUJUSEVIC M,MEADE D.Reliability evaluation and optimization of redundant dynamic systems[J].IEEE Transactions on Reliability,1985,34(2):171-174.
[7]ZHANG T J,REN S X,LI S G,et al.Application of the catastrophe progression method in predicting coal and gas outburst[J].Mining Science and Technology,2009,19(4):430-434.
[8] 杨懿,武昌,齐胜利.基于突变理论的维修保障系统效能评估研究[J].空军工程大学学报(自然科学版),2005,6(5):27-32.
YANG Yi,WU Chang,QI Shengli.Study of effective⁃ness evaluation of maintenance support system based on catastrophe theory[J].Journal of Air Force Engi⁃neering University(Natural Science Edition),2005,6 (5):27-32.
[9]陈晓红,杨立.基于突变级数法的障碍诊断模型及其在中小企业中的应用[J].系统工程理论与实践,2013,33(6):1479-1485.
CHEN Xiaohong,YANG Li.Obstacle diagnosis model based on the catastrophe progression method and its ap⁃plications for the small and medium-sized enterprises [J].Systems Engineering-Theory and Practice,2013,33(6):1479-1485.
[10]BEBBINGTON M,LAI C D,ZITIKIS R.Balancing burn-in and mission times in environments with cata⁃strophic and repairable failures[J].Reliability Engi⁃neeringandSystemSafety, 2009, 94(8):1314-1321.
[11] CAO W,ZHOU S L,WU S H.Land-use regionaliza⁃tion based on landscape pattern indices using rough set theory and catastrophe progression method[J]. EnvironmentalEarthSciences,2015,73(4):1611-1620.
[12]宫凤强,李夕兵,高科.地下工程围岩稳定性分类的突变级数法研究[J].中南大学学报(自然科学版),2008,39(5):1081-1086.
GONG Fengqiang,LI Xibing,GAO Ke.Catastrophe progression method for stability classification of un⁃derground engineering surrounding rock[J].Journal of Central South University(Science and Technolo⁃gy),2008,39(5):1081-1086.
[13]孙克宇,李若岩,王龙.海上协同交战仿真系统体系结构研究[J].系统仿真学报,2009,21(1):205-209.
SUN Keyu,LI Ruoyan,WANG Long.The research on architecture frameworks of navy cooperative war⁃fare simulation system[J].Journal of System Simula⁃tion,2009,21(1):205-209.
The comprehensive evaluation of naval vessel's engagement capability based on the catastrophe progression method
XIE Zongren1,LV Jianwei1,LIN Hua2
1 Department of Management Science and Engineering,Naval University of Engineering,Wuhan 430033,China
2 College of Electronic Engineering,Naval University of Engineering,Wuhan 430033,China
In order to meet the operational requirements of modern informational naval combat and the ob⁃jectives of carrying out diversified military missions,the evaluation method of naval vessel's cooperative en⁃gagement capability based on the catastrophe progression method is proposed.The method is based on the requirements of cooperative engagement in warship formations and basic principles and arithmetic process⁃es of catastrophe theories.According to catastrophe theories,an integrated indicator system is established,with factors affecting cooperative engagement capability as well as their catastrophe types being analyzed. The evaluation results are obtained after non-dimension alization of preliminary data and comprehensive quantitative calculation.Finally,the method is applied to the evaluation of several ships'combat effective⁃ness,and the results are proved to be true and accurate,which provides a new perspective for the evalua⁃tion of naval vessel's cooperative engagement capability.
catastrophe progression method;naval vessels;engagement capability;evaluation
U674.7+02
A
10.3969/j.issn.1673-3185.2016.03.002
2015-08-22网络出版时间:2016-5-31 11:04
国家自然科学基金资助项目(71401171);国家部委基金资助项目作者简介:谢宗仁,男,1990年生,博士生。研究方向:装备系统建模与仿真。
E-mail:wx18392015@163.com
吕建伟(通信作者),男,1962年生,博士,教授。研究方向:系统工程。
E-mail:L2015wh@163.com

