基于正交投影矩阵的强弱信号闭环测向方法

张　倩， 陶海红， 张博一

(西安电子科技大学 雷达信号处理国家重点实验室， 西安　710071)



基于正交投影矩阵的强弱信号闭环测向方法

张倩， 陶海红， 张博一

(西安电子科技大学 雷达信号处理国家重点实验室， 西安710071)

当空间中强弱信号同时存在时,由于强信号对弱信号的压制,使得弱信号的方向估计性能变差,甚至无法测得。针对赋形天线系统,提出了一种基于正交投影矩阵的强弱信号闭环测向算法。利用闭环测向算法估计出强信号方向,根据强信号的方向基于线性约束最小方差(LC-MV)准则构造正交投影矩阵;对赋形天线接收数据进行滤波,抑制掉强信号;根据强信号方向产生LCMV权作为初始权值进行闭环迭代,实现对弱信号的测向。实验表明:该方法在强弱信号并存的情况下可以实现强弱信号的方向估计。

赋形天线;正交投影矩阵;强弱信号;闭环测向;方向估计

0　引　　言

对于强弱信号共存的情况， 传统的测向算法很难测出弱信号的方向， 尤其是当强信号和弱信号空间位置很接近时， 弱信号的谱峰通常被强信号的谱峰所掩盖。 要实现强信号环境下弱信号的测向， 首先要消除强信号的影响。 消除强信号常见的思路有两种： 一是先估计出强信号的相关参数， 恢复强信号， 并从接收信号或其协方差矩阵中减去强信号分量； 二是设计加权矢量， 此加权矢量与强信号方向矢量正交， 以抑制强信号， 接收信号通过加权矢量处理后强信号分量得到滤除。 针对这两种思路， 国内外已发表了大量文献。 文献[1]提出一种干扰阻塞(JJM)算法， 利用强信号波达方向(DOA)精确已知的先验信息对阵列流形矩阵进行降秩处理， 以抵消强信号的作用， 再利用传统的空间谱估计算法实现弱信号的DOA估计。 该方法以损失阵列孔径为代价。 文献[2-3]将JJM算法推广至二维DOA估计， 且文献[2]给出一种基于正交投影预变换的弱信号测向算法。 文献[4]提出利用子阵划分来估计弱信号方向的方法， 在每个子阵上进行波束形成以有效抑制强信号。 该方法局限于阵列的形式， 实现复杂。 上述方法都是基于开环算法。 本文提出的基于正交投影矩阵的强弱信号闭环测向算法， 根据强信号的方向信息构造正交投影矩阵[5]， 对天线接收数据进行滤波， 抑制强信号， 利用最小均方(LMS)算法对滤波后数据进行波束形成， 从而实现弱信号的DOA估计。 该算法不拘泥于阵型， 实现简单。

1　多波束赋形天线系统信号模型

多波束赋形天线通过多个点状窄波束赋形实现宽空域覆盖。 考虑由7个馈源组成天线阵列， 每个馈源产生一个点状波束， 即每个阵元均为定向天线。 7个阵元采用蜂窝状布阵， 如图1所示。

图17阵元阵列排布

1.1阵列接收数据模型

图1中， 七个阵元坐标分别为(xk,yk),k=1,2，…,7， 则第k个阵元接收到的信号为

(1)

式中： si(t)为参考阵元接收到的第i个信号； p为信号源数目； nk(t)为第k个通道接收到的噪声， 假设为高斯白噪声； 设信号二维方向[6]分别为(θi,φi)， i=1,2,…,p， 则τki为第i个信号到达第k个阵元相对于参考阵元的时延， 则

(2)

式中： c为电磁波的传播速度。

根据单个阵元的信号接收模型可得， 窄带情况下阵列接收信号为

(3)

式中：a(θi,φi)为第i个信号源的导向矢量， 将第1个阵元作为参考阵元， 则

(4)

(5)

1.2赋形天线系统信号模型[7]

赋形天线系统的合成波束为

(6)

式中： X=[X1,X2, …,X7]T为子波束构成的矢量；W=[w1， w2， …， w7]T为自适应波束权值； Wq=[wq1，wq2， …，wq7]T为初始静态权值。

仿真用的天线方向图基于实际天线测得， 其波束合成静态方向图如图2所示。

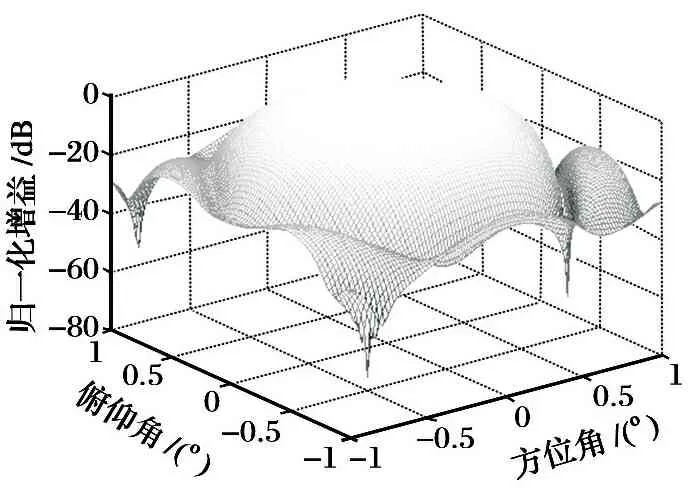
图2天线合成静态方向图

2　基于正交投影矩阵的强弱信号闭环测向算法

2.1强信号闭环测向算法

要实现对强信号的闭环测向， 针对阵列接收数据， 首先要实现对强信号的闭环调零， 然后根据零陷位置估计强信号的方向。

2.1.1基于LMS的闭环调零算法

采用基于LMS[8]的闭环迭代算法进行权值W的更新， 实现闭环调零。 LMS空域自适应波束形成原理框图如图3所示。

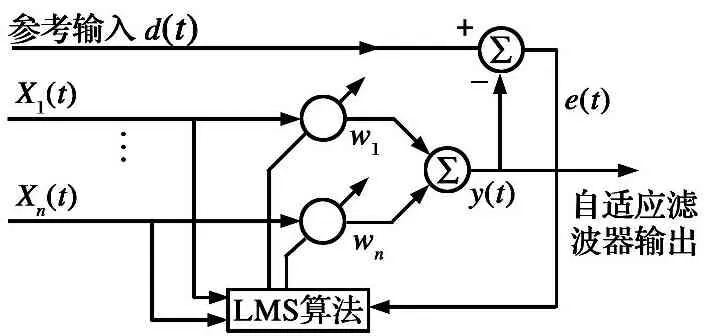
图3LMS空域自适应波束形成原理框图

设t时刻7个阵元接收到的信号为X(t)， 则波束形成为

y(t)=WHX(t)

(7)

设期望信号d(t)与波束形成后输出y(t)的误差为e(t)， 则

e(t)=y(t)-d(t)

(8)

均方误差δ为

(9)

式中： Rx=E[X(t)XH(t)]为输入各阵元支路的自相关矩阵；rxd为各支路输入与期望输出的互相关。

d*(t))]=2E[X(t)e*(t)]

(10)

用瞬时值代替稳态值：

(11)

得到最优权矢量的迭代公式：

(12)

式中：W的初始值为赋形天线静态权值Wq; μ为迭代步长因子。

2.1.2闭环测向算法原理

闭环测向算法是在开环MUSIC测向方法的基础上加以改进得到的， 基本思想是通过迭代调整阵列权值W使阵列输出功率最小， 并且阵列方向图在信号方向形成零陷。 随着迭代收敛， 阵列最终输出的能量最小：

(13)

(14)

在式(14)的基础上结合多波束赋形方向图， 实现闭环测向的算法， 测向的空间谱函数定义为

(15)式中：B(θ,φ)=[b1(θ,φ),b2(θ,φ), …,b7(θ,φ)]T；bi(θ,φ), i=1, 2, …, 7为第i个点波束的方向图。

可知， 闭环测向是在闭环调零的基础上对调零后的值取导数， 再进行谱峰搜索而实现的， 因此， 对信号位置实现准确零陷是实现准确测向的前提。

2.2弱信号测向

2.2.1抑制强信号的空域滤波算法[9-10]

应用式(15)准确估计出强信号方向后采用如下准则抑制强信号：

(16)

s.t.AHW=0

(17)

式中： W为天线的调零权矢量; Wq为未调零时的波束合成静态权矢量。 式(16)表示天线调零后的波束要尽量保持原形， 以免影响正常通信， 即波束保形； 式(17)表示在强信号方向形成零陷的自适应加权。 解得：

Wopt=Q⊥Wq

(18)

式中： Q⊥为强信号导向矩阵A的正交投影矩阵, 即

Q⊥=I-A(AHA)-1AH

(19)

2.2.2弱信号测向

与强信号的测向算法相同， 首先利用LMS对滤除强信号后的数据X′=Q⊥X进行闭环调零， 在弱干扰位置形成零陷， 再根据式(15)实现弱信号的闭环测向。

2.3强弱信号闭环测向算法

基于正交投影矩阵的强弱信号闭环测向算法流程图见图4。 对于一强一弱两个信号的情况， 首先对7个阵元接收到的数据X实现闭环测向算法， 闭环迭代的初始权值为Wq， 得到强信号的方向信息。 然后利用强信号的导向矢量产生正交投影矩阵Q⊥， 并利用正交投影矩阵修正接收数据X以抑制强信号， 从而产生新的7路数据： X′=Q⊥X。 对新产生的数据X′， 再应用闭环迭代算法进行测向。 在这次迭代过程中， 将强信号方向产生的LCMV权Wopt=Q⊥Wq作为迭代的初始权， 实现弱信号的闭环测向。

3　算法仿真与性能分析

仿真条件： 一强一弱信号， 信号的方位角与俯仰角分别为强信号(0.4°， -0.1°)， 弱信号(-0.2°， 0°)； 中心频率为40 GHz； 强干扰和弱干扰的频率分别为40.105 GHz和40.165 GHz； 采样频率为500 MHz。

图4基于正交投影矩阵的强弱信号闭环测向算法流程图

实验1： 测向性能仿真

仿真结果如图5所示。 图5(a)为强信号闭环调零的仿真结果， 在强信号处产生零陷， 而在弱信号方向没有零陷； 图5(b)为强信号闭环测向的仿真结果， 只测得强信号方向， 而弱信号方向没有测得； 图5(c)为过滤掉强信号后的弱信号闭环调零仿真图， 相比图5(a),图5(c)在弱信号方向产生零陷； 图5(d)为利用本文算法进行弱信号闭环测向的仿真图， 该方法成功地抑制掉强信号， 测得弱信号的方向。

实验2～4对强信号方向精确测得情况下的弱信号方向估计误差进行分析。

实验2： 强弱信号能量差对测向性能的影响

图5基于LMS的强弱信号闭环测向

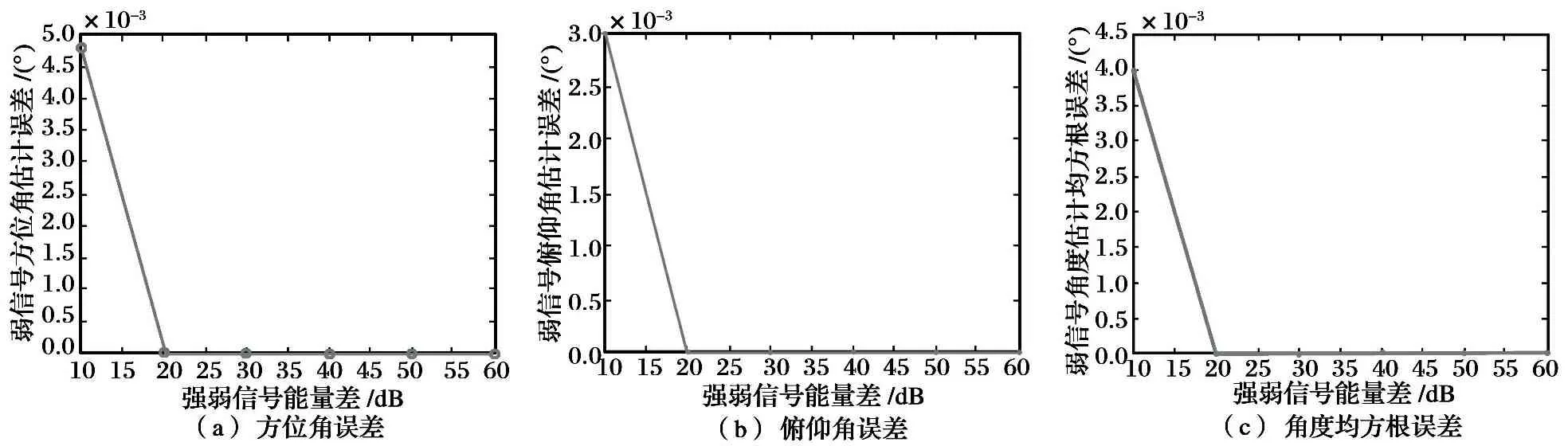
弱信号角度估计误差与强弱信号能量差的关系见图6。

(20)

图6弱信号角度估计误差与强弱信号能量差关系

式中：θ实为实际方位角；φ实为实际俯仰角；θ估为采用本文方法得到的方位角度的估计值；φ估为采用本文方法得到的俯仰角的估计值。 下文中的角度均方根误差均采用式(20)求得。

实验3： 弱信号闭环测向的迭代次数对测角性能的影响

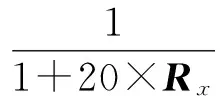
弱信号测向误差与迭代次数的关系如图7所示。 由仿真结果可以看出， 随着迭代次数的增加， 测角误差趋于稳定。 当迭代次数大于20， 角度估计均方根误差收敛为0。

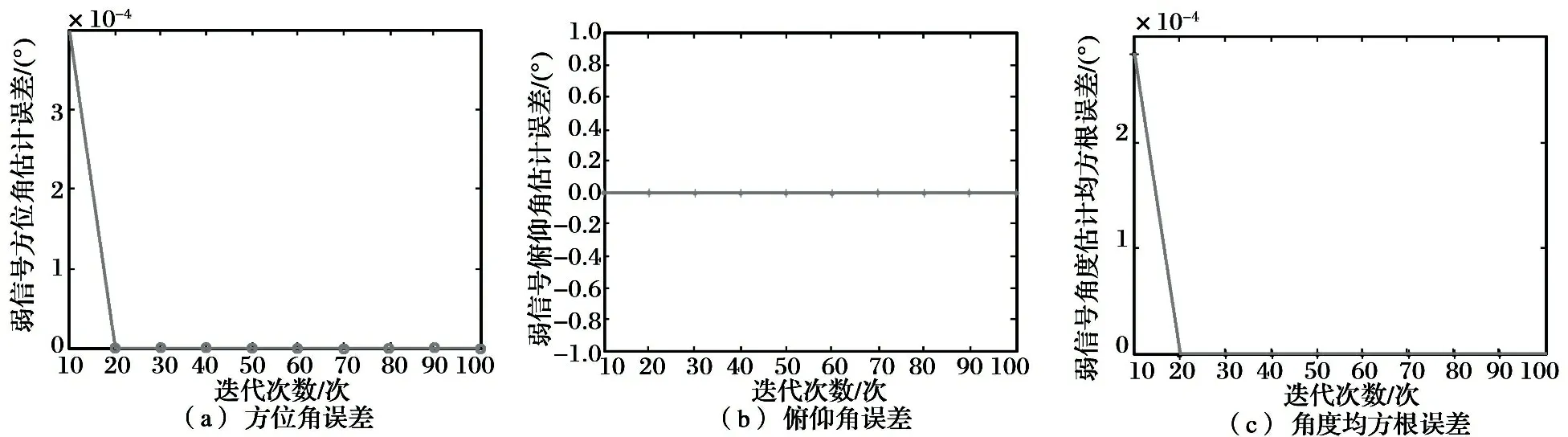
图7弱信号测向误差与迭代次数关系

实验4： 强弱信号角度间隔对闭环测向性能的影响

(1) 固定强信号的方向和弱信号的俯仰角， 弱信号的方位角从0°到0.4°以步长0.1°变化， 每次角度变化做100次蒙特卡洛实验。 弱信号测向误差与强弱信号方位角间隔关系如图8所示。

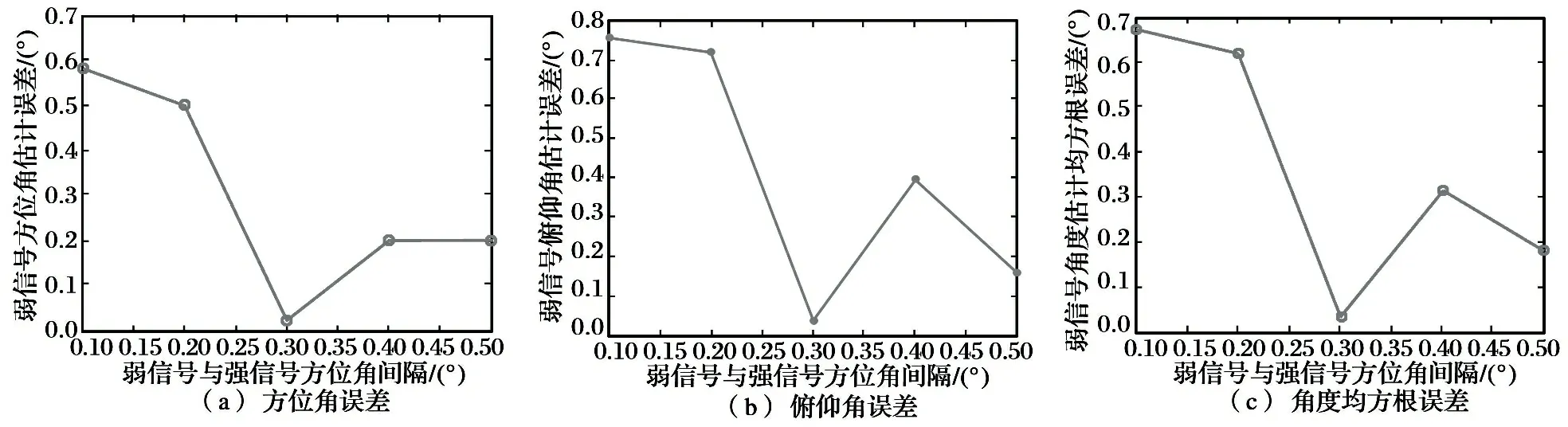
图8弱信号测向误差与方位角间隔关系

(2) 固定强信号的方向和弱信号的方位角， 弱信号的俯仰角从-0.5°到-0.1°以步长0.1°变化， 每次角度变化做100次蒙特卡洛实验。 弱信号测向误差与强弱信号俯仰角间隔关系见图9。

由仿真结果可以看出， 随着角度间隔变大， 测角误差会有起伏， 但是总体趋势为误差减小。

图9弱信号测向误差与俯仰角间隔关系

实验5： 角度搜索步长对闭环测向精度的影响

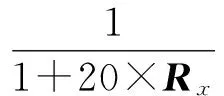
强信号方向为(0.42°， -0.1°)， 弱信号的方向为(-0.22°， 0.01°)， 改变角度的搜索步长， 分别以步长0.01°， 0.02°， 0.04°进行角度搜索， 每个步长做100次蒙特卡洛实验。 强弱信号测向误差与角度搜索步长的关系如图10所示。

由仿真结果可以看出， 测角精度与角度搜索步长有关， 角度搜索步长越大， 测角估计误差越大， 测角精度越差。

图10强弱信号测向误差与角度搜索步长的关系

4　结　　论

本文提出的基于正交投影矩阵的强弱信号闭环测向方法， 利用闭环测向算法估计出强信号的DOA， 根据强信号的精确测向构造正交投影矩阵， 实现对接收数据中强弱信号的闭环测向。 与文献[11]提出的方法都属于基于自适应迭代的强弱信号估计方法。 仿真结果表明， 该方法能有效抑制强干扰对弱干扰的影响， 实现多波束域系统中弱信号的方向估计， 且不受阵型限制， 不用考虑阵列孔径损失， 实现简单。

[1] 陈辉,苏海军. 强干扰/信号背景下的DOA估计新方法[J]. 电子学报， 2006, 34(3): 530-534.

[2] 王鼎, 张莉, 吴瑛. 两种强干扰下弱信号的二维波达方向估计算法研究[J]. 系统仿真学报， 2009, 21(10): 2866-2871.

[3] 徐亮. 强弱信号测向算法研究[D]. 西安： 西安电子科技大学， 2011.

[4] 柴立功, 罗景青.一种强干扰条件下微弱信号DOA估计的新方法[J]. 电子与信息学报， 2005, 27(10): 1517-1520.

[5] 苏成晓, 罗景青. 基于正交投影变换的宽带弱信号测向算法[J]. 电子信息对抗技术， 2014, 29(1): 16-20.

[6] 吴湘霖， 俞卞章.基于任意结构阵列的二维波达方向与频率联合估计[J].航空兵器， 2008(2): 39-42.

[7] 侯颖妮, 黄建国, 冯西安. 基于多波束系统的波束域方位估计方法研究[J]. 弹箭与制导学报， 2007, 27(3): 80-82.

[8] 张贤达.现代信号处理[M].北京： 清华大学出版社， 2002： 188-205.

[9] 甘泉, 孙学军, 唐斌. 一种基于空域滤波的空间谱估计方法[J]. 信号处理， 2010, 26(2): 230-233.

[10] 易岷, 肖先赐. 阵列信号处理中强弱信号同时测向与分辨[J]. 通信对抗， 2005(3): 9-12.

[11] 刘永军, 廖桂生, 杨东. 基于自适应迭代的强弱信号波达方向估计[J]. 电子学报， 2015, 43(7):1425-1431.

Closed Loop Direction Finding Algorithm of Strong and Weak Signals Based on Orthogonal Projection Matrix

Zhang Qian, Tao Haihong, Zhang Boyi

(State Key Lab of Radar Signal Processing, Xidian University, Xi’an 710071, China)

When strong and weak signals exist at the same time, due to the suppression of strong signal, it is difficult to estimate the direction of arrival (DOA) of weak signal. For the shaped array system， a closed loop direction finding algorithm based on orthogonal projection matrix is proposed. The DOA of strong signal is estimated by the closed loop direction finding algorithm, and according to the DOA of strong signal, the orthogonal projection matrix is structured based on linear constrained minimum variance(LCMV) criterion. The filtering is carried out for shaped antenna receiving data to suppress strong signal. The LCMV weight produced by the DOA of strong signal is taken as initial weight and closed loop iteration is performed to estimate the DOA of weak signal. Experiments show that the DOA estimation of strong and weak signals can be realized when strong and weak signals exist at the same time.

shaped array; orthogonal projection matrix; strong and weak signals; closed loop direction finding； DOA

10.19297/j.cnki.41-1228/tj.2016.03.008

2015-08-31

航空科学基金项目(20120181009)

张倩(1993-)， 女， 陕西咸阳人， 硕士研究生， 研究方向为阵列信号处理。

TN911.23

A

1673-5048(2016)03-0035-06