巡飞武器气动/结构/隐身一体化设计及多学科优化设计

胡　劲， 刘　涛， 张　鹏， 欧　军， 魏树孝， 高　辉， 吴　波， 闫君丹

(中航工业洪都， 南昌　330024)



巡飞武器气动/结构/隐身一体化设计及多学科优化设计

胡劲， 刘涛， 张鹏， 欧军， 魏树孝， 高辉， 吴波， 闫君丹

(中航工业洪都， 南昌330024)

巡飞武器不仅需要满足续航时间的要求， 还应尽量降低其RCS值以提高战场生存能力， 同时还要满足结构尺寸、 质量及结构特性的要求。 本文对巡飞武器气动/结构/隐身一体化设计及多学科优化问题进行了研究， 建立了气动/结构/隐身一体化优化模型和分析流程， 优化了巡飞武器总体参数， 改良了巡飞武器的总体性能。

巡飞武器； 气动/结构/隐身； 一体化设计； 多学科设计优化

0　引　　言

优化设计的首要任务是对优化问题进行科学合理的描述， 欲清楚地描述巡飞武器气动/结构/隐身一体化优化问题， 应对巡飞武器的使用特点有一个清晰的认识， 在此基础上寻找巡飞武器的关键性能指标， 围绕这些指标建立巡飞武器的优化问题模型。

由于巡飞武器的飞行任务主要集中在对目标区域的巡逻搜索阶段， 该阶段的续航时间对巡飞武器的任务效能起着决定性的作用， 且巡逻搜索阶段对目标进行搜索或监视时容易遭受敌方防空火力的攻击。 因此， 缩减巡飞武器的雷达散射截面对于提高巡飞武器的战场生存能力有重要意义。 同时， 受发射条件和飞行使用的约束， 还需考虑对巡飞武器质量、 外形尺寸的约束， 以及运输、飞行性能对结构特性的要求。

1　优化设计问题描述

选取巡飞武器巡逻搜索阶段的续航时间Tcruise和周向RCS平均值作为评价巡飞武器性能的指标， Tcruise表征了巡飞武器执行侦察打击任务的持续作战能力， 周向RCS平均值表征了巡飞武器的战场生存能力。

采用活塞发动机的巡飞武器续航时间为

(1)

式中： ηp为螺旋桨效率； K为巡飞武器升阻比； Ce为发动机耗油率； Vloi为巡飞武器巡逻飞行速度。

巡飞武器初始质量：

m0=mf+ms+mother

(2)

其中： mf为燃料质量； ms为巡飞武器结构质量； mother为除去燃料和结构的其他质量。

则式(2)可变为

(3)

通过升阻比K和ms将气动学科和结构学科统一到巡飞武器续航时间这一指标中。 优化问题的具体模型如图1所示。

图1巡飞武器气动/结构/隐身一体化优化模型

图中， X1为巡飞弹几何外形参数， 作为系统级设计变量； X2为巡飞弹结构部件尺寸参数， 作为结构学科二级优化设计变量。

整个优化过程包含两级优化： 一个是系统级优化， 设计变量为巡飞武器几何外形参数， 目标函数为巡飞武器续航时间和周向RCS均值， 约束为弹体长度不大于给定值， 具体模型如式(4)所示:

s.t.Length≤3 500mm

X∈[Xmin, Xmax]

(4)

式中： Length为巡飞武器弹体长度； X为设计变量。

第二级优化包含在结构模块中， 是针对巡飞武器结构质量的优化， 设计变量为巡飞武器结构部件尺寸参数， 主要是弹身隔板、 梁、 蒙皮， 弹翼翼梁、 翼肋、 蒙皮厚度等， 目标函数为结构质量， 约束为最大应力小于给定值， 具体模型如式(5)所示:

(5)

本文所选取的优化设计点处于巡飞武器巡逻飞行过程中， 巡飞武器所受的载荷并非其最大载荷， 为保证巡飞武器结构强度满足整个飞行过程(尤其是末端机动时过载最大)的要求， 使其最大许用应力σ*处于一个较低的应力水平。

为减小阻力， 巡飞武器在巡逻飞行过程中攻角变化不大， 一般在0°～4°之间， 保持在一个小的攻角范围内飞行可以使巡飞武器拥有较为稳定的气动特性和操纵特性。 且光电载荷对地面观测(成像)的姿态也需要巡飞武器在巡飞过程中保持一个较小的攻角变化。 本文以2°攻角的升阻比作为巡飞过程中的平均升阻比， 优化设计点的攻角α=2°。

2　巡飞武器参数化建模

2.1翼型参数化模型

采用CST方法对翼型进行参数化表示，CST参数化方法是近年来出现的一种比较优秀的参数化方法， 具有设计变量少、可调节、设计空间广等优点， 被广泛用于翼型设计中。

翼型采用CST方法参数化的表达式如下：

(6)

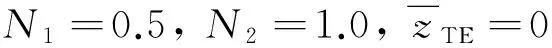
图2NACA6412的5阶CST拟合效果

采用5阶伯恩斯坦多项式。

2.2弹身参数化模型

2.2.1弹身截面形状

设计过程中将巡飞武器弹身截面形状以xz平面分为上下两条曲线， 如图3所示， 分别进行参数化。

图3弹身截面形状示意图

参数化方法采用前文论述的CST方法， 形状函数采用6阶伯恩斯坦多项式加权形式：

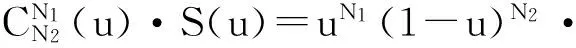
(7)

对于对称构型的曲线， 式(7)中存在以下关系：

因此描述一条对称曲线的CST公式变为

ζ(u)=C(N,u)·S(u)=uN(1-u)N·

(8)

描述弹身截面的公式为

(9)

式中： Nu,Nd为类函数中的N； ui,di为形状函数中的伯恩斯坦系数。

加权伯恩斯坦多项式：

(10)

只需要N, b0, b1, b24个参数就可以描述一条对称曲线。 所以用Nu, Nd, ui, di(i=0, 1, 2)8个参数就可以完全描述弹身截面形状。

2.2.2弹身侧向轮廓

为充分利用约束空间， 弹身宽度定为约束最大尺寸， 头部为一小段圆弧与弹身侧面直线用连接线相切连接形成的曲线， 尾部为一小段斜线与弹身侧面直线用连接线相切连接形成的曲线， 形成的弹身侧向轮廓如图4所示。

图4弹身侧向轮廓示意图

弹体长度为各舱段长度之和。 燃料舱长度为

(11)

式中： mf为燃油质量； ρf=720kg/m3为燃油密度； Sbody为弹身截面积； ks为弹身截面利用效率。

3　多学科建模分析

3.1气动特性分析流程

气动特性分析模型的工作流程如图5所示， 分析模型的输入为巡飞武器几何外形的参数， 输出为巡飞武器的升、 阻力系数和表面载荷文件用于有限元分析。

图5气动特性分析流程

3.2结构分析流程

结构分析工具采用MSC.PATRAN&NASTRAN， 流程见图6， 输入为巡飞武器几何外形参数， 输出为巡飞武器最小质量。 在分析过程中采用软件本身的结构优化功能， 对巡飞武器结构部件的尺寸进行优化。 分析过程中的载荷来自于气动特性分析模块， 采用三角形面积加权方法将由气动计算得到的气动网格上的节点力转化到结构网格上。

3.3RCS分析流程

隐身特性分析流程见图7。 本文基于第2节建立的参数化几何外形， 利用CATIA软件AdvancedMeshingTools模块生成用于RCS计算的表面网格， 利用物理光学法程序计算巡飞武器的RCS值。

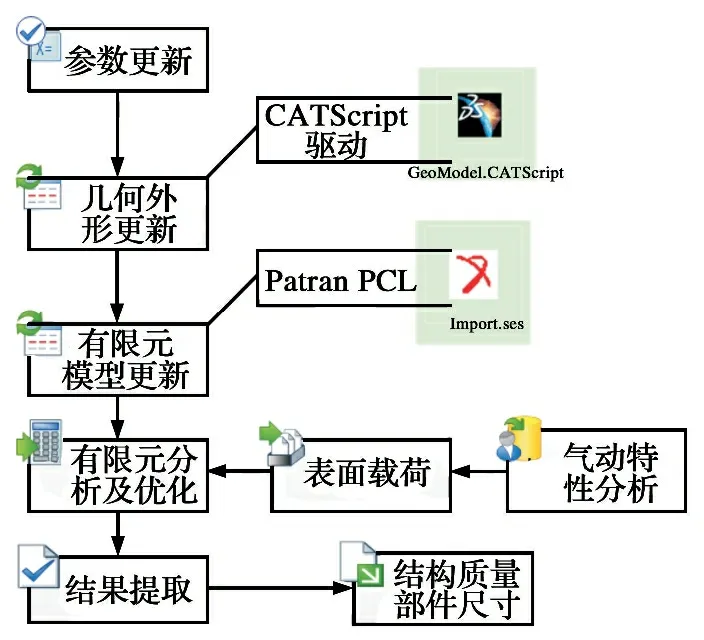
图6　巡飞武器结构有限元分析流程图

图7隐身特性分析流程图

3.4气动/结构/隐身一体化分析流程

将上述三个学科的分析模型综合在一起形成如图8所示的气动/结构/隐身一体化分析模型。

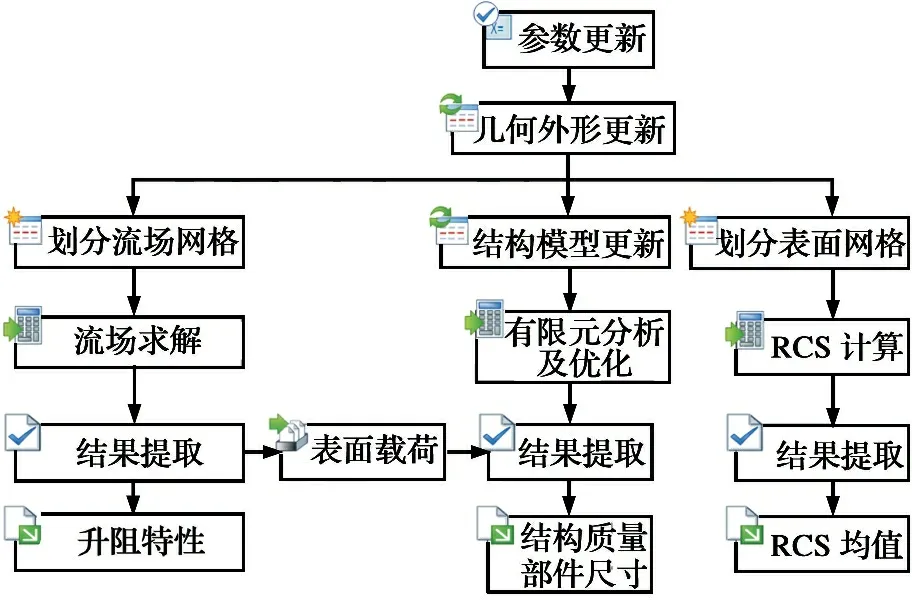
图8气动/结构/隐身一体化分析流程

4　多学科优化设计

4.1代理模型结果

本文利用Isight软件搭建一体化优化模型， 首先利用响应面方法建立了弹身长度、 阻力系数和升力系数的代理模型， 利用Kriging方法建立了周向RCS均值和全弹质量的代理模型， 最终搭建起来的气动/结构/隐身一体化优化模型如图9所示。 采用Isight内置的NSGA-II优化算法， 种群规模为52， 迭代次数为500， 交叉概率为0.9。 迭代500步后得到的种群分布情况如图10所示。

图9　巡飞弹气动/结构/隐身一体化优化模型

图10迭代500步后的种群分布情况

巡飞武器气动/结构/隐身一体化多目标优化的Pareto前沿如图11所示。 本文从中选取了两种方案， 方案一表征续航时间最优状态， 方案二表征隐身特性最优状态。 在优化前沿曲线上， 越靠近右端对应设计方案的续航时间越好而隐身特性越差， 即周向RCS均值越大。

图11巡飞武器气动/结构/隐身一体化优化Pareto前沿

4.2优化结果分析

4.2.1气动特性对比

方案一较方案二有更高的升组比， 由气动外形差异引起。 首先， 方案一的弹翼是平直翼， 在低速情况下拥有比前掠翼更好的气动特性。 其次， 方案一翼展更大， 拥有较大的翼面积， 见图12。

4.2.2续航时间对比

两种方案在巡飞过程中的攻角变化曲线见图13。 方案一的攻角比方案二小， 巡飞阻力小， 经过仿真分析， 方案一的续航时间约为8.65h， 方案二的续航时间约为7.31h， 因此方案一在续航性能上较优。

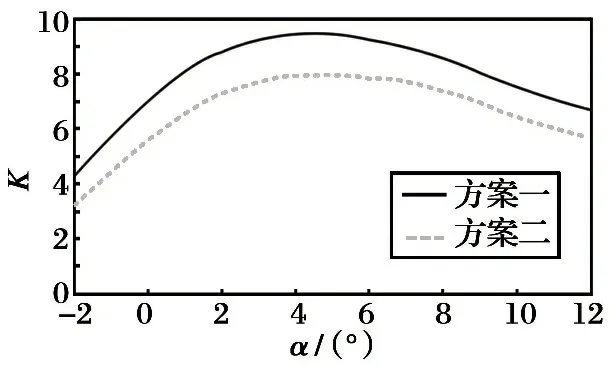
图12　两种方案的升阻比曲线

图13巡飞过程中的攻角变化曲线

4.2.3RCS对比

两种方案在直角坐标系下的RCS分布图如图14所示。 由于方案一和方案二几何外形相似， 因此两种方案的RCS分布曲线的趋势是相像的， 而两种方案RCS分布情况所展现的差异主要源于弹翼形状和弹身形状的差别。 在135°和225°两个位置都存在尖峰(负值)， 是因为弹身是周向最大反射源； 在90°和270°附近， 方案二RCS值比方案一小， 经过分析， 方案一RCS均值为0.71m2， 方案二RCS均值为0.44m2， 方案二优于方案一。

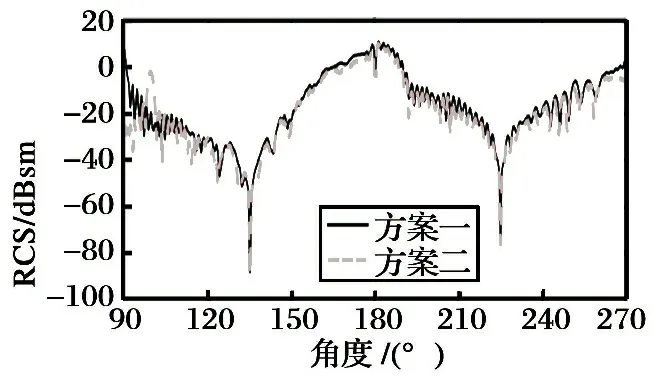
图14两种方案的RCS分布(直角坐标)

4.2.4结果

通过对两个设计方案在几何外形、 气动特性、 结构校核、 续航时间、 隐身特性方面的对比分析， 可以发现方案一较方案二在气动特性方面有着较大的优势， 这也直接导致其续航时间大于方案二， 但是在隐身特性方面方案二要优于方案一， 对于追求巡飞武器长时间滞空能力的设计时应倾向于方案一。

5　结　　论

本文对巡飞武器气动/结构/隐身一体化设计及多学科优化问题进行了研究， 介绍了一体化设计与优化问题的描述思路， 以及武器参数化模型建立方法， 建立了气动/结构/隐身一体化优化模型和分析流程。 通过优化对比其中两个方案， 证明通过多学科优化改进了巡飞武器的总体性能， 满足实际作战性能要求。

[1] 谷良贤， 阳建新， 温炳恒.导弹总体一体化设计方法研究[J]. 弹箭与制导学报， 1994(2): 1-5.

[2] 王志刚， 严辉， 陈士橹. 轨迹/飞行器总体参数的一体化优化方法研究[J]. 飞行力学， 1997(2): 19-26.

[3] 孟捷， 徐浩军， 葛志浩.飞行仿真中气动特性数据拟合方法研究[J]. 电光与控制，2007，14(4)：120-123.

[4] 叶庆凯, 王肇明. 优化与最优控制中的计算方法[M]. 北京： 科学出版社， 1986.

[5] 李忠应. 最优过程理论及其在飞行力学中的应用[M]. 北京： 北京航空航天大学出版社， 1990.

[6] 严辉. 飞行器系统最优原理及应用[D]. 西安： 西北工业大学， 1996.

[7] 余雄庆. 多学科设计优化算法及其在飞行器设计中的应用研究[D]. 南京： 南京航空航天大学， 1999.

Aerodynamics/Structure/Invisibility Integrative Design and Multidisciplinary Design Optimization of Loitering Weapon

Hu Jin, Liu Tao, Zhang Peng, Ou Jun, Wei Shuxiao, Gao Hui, Wu Bo, Yan Jundan

(AVIC Hongdu Aviation Industry Group, Nanchang 330024, China)

The loitering weapon not only needs to meet the requirements of life time, but also needs to reduce its RCS value in order to improve the survival ability of battlefield. Meanwhile, the requirements of structure size, quality and structure characteristics should be met. The integrated design of aerodynamics/structure/invisibility on loitering weapon and multidisciplinary optimization problems are studied, and the integrated optimization model and analysis process of aerodynamic/structure/invisibility are established. The overall parameters of loitering weapon are optimized, and its overall performance is improved.

loitering weapon; aerodynamics/structure/invisibility; integrative design; multidisciplinary design optimization

10.19297/j.cnki.41-1228/tj.2016.03.002

2015-09-09

胡劲(1985-)， 男， 新疆石河子人， 工程师， 研究方向为无人飞行器总体设计。

V221

A

1673-5048(2016)03-0009-05