基于有限时间控制方法的三维空间导弹制导律设计

李友年, 江　云, 李世华, 张振兴

(1. 中国空空导弹研究院， 河南 洛阳　471009； 2. 东南大学 自动化学院， 南京　210096)



基于有限时间控制方法的三维空间导弹制导律设计

李友年1, 江云1, 李世华2, 张振兴2

(1. 中国空空导弹研究院， 河南 洛阳471009； 2. 东南大学 自动化学院， 南京210096)

针对三维空间导弹拦截机动目标问题,提出了一种基于有限时间反馈控制方法的新型制导律。该制导律将目标加速度视作制导系统的外部有界扰动,并引入切换函数来抑制系统扰动,经过严格的理论分析证明视线角速率能够在有限时间收敛到零。数值仿真结果验证了所提方法的有效性。

导弹;目标机动;三维空间制导律;有限时间控制

0　引　　言

制导律的设计目标是为自动驾驶仪提供加速度指令， 使得导弹获得最小的脱靶量， 从而有效地实现导弹对目标的拦截， 因此， 制导律设计是实现精确制导的基础[1]。 在传统的三维制导律设计中， 通常采用双平面解耦的设计思想[2]， 即在视线角和视线角速率比较小的情况下， 导弹-目标的相对运动方程能在理想的碰撞点附近进行线性化，将三维空间导弹-目标相对运动模型简化成两个二维平面导弹-目标相对运动模型， 然后分别设计制导律。 这种方法由于设计相对简单、 可实现性强而被广泛采纳。 但是当目标作快速机动飞行时， 视线角和视线角速率比较小的假设不再成立， 两个平面之间存在耦合关系， 这给基于双平面解耦的制导律设计带来了困难。 因此， 研究三维空间导弹制导律对提高导弹拦截大机动目标的制导精度是非常有必要的。

文献[3]针对耦合的三维空间制导模型， 研究了比例制导律； 文献[4]基于李雅普诺夫稳定性方法， 推广了文献[3]中的比例制导律； 针对导弹拦截机动飞行目标问题， 文献[5]扩展了文献[4]中比例制导律的设计方法； 文献[6]针对导弹拦截机动目标问题， 研究了最优制导律设计方法， 其基于李群方法， 通过SO(3)群描述了导弹-目标相对运动关系， 计算得到了非解耦条件下的三维制导律； 文献[7]基于微分几何方法， 设计了不依赖于剩余飞行时间的三维鲁棒制导律； 文献[8]基于L2/H∞控制方法， 设计了三维鲁棒制导律； 文献[9]基于RBF神经网络方法， 设计了一种根据视线角速率变化情况， 动态调节非线性制导律增益的鲁棒控制律； 文献[10]基于θ-D次最优控制方法， 设计了闭环形式的三维末制导律； 文献[11]通过扩展圆轨迹导引算法， 设计了带碰撞角约束的三维制导律。 以上这些制导律是基于渐近收敛理论设计的， 随着导弹技术的不断发展， 导弹的飞行速度不断提升， 精度要求也在不断提高， 高速导弹在拦截目标的制导过程中， 末制导时间很短甚至只有几秒， 研究具有快速收敛特性的制导律是非常有必要的。 在实战中， 目标机动性能也随着先进技术的应用而不断提高， 因此研究具有抗目标机动性能的制导律也是非常有必要的。

本文针对三维空间导弹拦击机动目标问题， 基于有限时间反馈控制方法提出了一种新型制导律设计方法。

1　三维空间导弹-目标相对运动方程

三维空间中导弹-目标的相对运动如图1所示。 图中，M-XYZ为原点与导弹质心重合的惯性坐标系；φ为导弹-目标的视线倾角， 其定义为视线与水平面MXY之间的夹角；θ为导弹-目标的视线偏角， 其定义为视线在水平面的投影与惯性系的MX轴之间的夹角；r为导弹-目标之间的距离。 (r,φ,θ)为原点在目标质心M的球坐标系， 其坐标轴矢量的单位矢量为(er,eθ,eφ)， 其中， er与视线方向重合， 由导弹指向目标为正；eθ位于包含er的纵向平面内， 指向上方为正；eφ方向按右手定则确定。

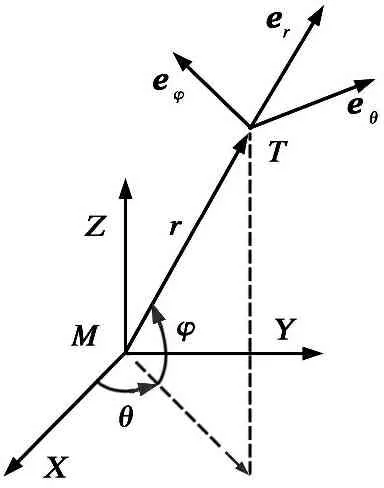
图1三维空间中导弹-目标的相对位置

导弹-目标的相对运动关系的极坐标方程为

(1)

(2)

(3)

其中： (atr, atθ, atφ)为目标加速度在球面坐标系(er,eθ,eφ)上的分量； (amr, amθ, amφ)为导弹加速度在球面坐标系(er, eθ, eφ)上的分量。

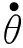
(4)

(5)

假设1： 假设目标加速度atθ(t)和atφ(t)有界且满足|atθ(t)|≤dθ， |atφ(t)|≤dφ， 其中dθ和dφ为目标加速度atθ(t)和atφ(t)的上界。

2　有限时间稳定性定义及判定定理

在设计有限时间制导律之前， 先给出非线性系统有限时间稳定的定义和引理。 考虑如下非线性系统：

(6)

其中： f(x):U→Rn为在包含原点的开区域U上对x的连续函数。

定义1：考虑式(6)， 系统的平衡点x=0为有限时间稳定的当且仅当满足如下两个条件[9]：

(1) 系统在零点的一个开区域U0⊂U内是Lyapunov稳定的；

(2) 系统在U0内是有限时间收敛的， 即对任意的初始值x0∈U0/{0}， 存在过渡时间T(x0)≥0， 使得定义在t∈[0,T(x0))上式(6)的解x(t,x0)∈U0/{0}满足

(7)

若U=U0=Rn， 则原点是全局有限时间稳定的平衡点。

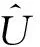
(8)

3　三维有限时间制导律设计

定理1： 考虑三维空间制导系统式(4)～(5)。 如果假设1和假设2成立， 则三维空间有限时间制导律如下：

k1rcosφ|x1|α1sign(x1)+ε1sign(x1)

(9)

k2r|x2|α2sign(x2)+ε2sign(x2)

(10)

证明： 将式(9)代入式(4)， 将式(10)代入式(5)得到闭环系统方程：

(11)

(12)

取Lyapunov函数

(13)

对式(13)求一阶导数并带入式(11)和(12)得

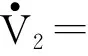
(14)

(15)

(16)

于是， 式(14)可以化简为

(17)

4　数值仿真

仿真条件： 导弹初始位置xM0=0m， yM0=0m， zM0=0m； 导弹初始速度VM0=800m/s； 导弹初始飞行方位角度φM=15°， θM=5°； 目标初始位置xT0=5 000m， yT0=4 000m， zT0=200m； 目标飞行速度VT0=600m/s； 目标初始飞行方位角度φT=10°， θT=5°； 重力加速度g=9.8m/s2； 导弹最大加速度输出为40g。

选取如下传统比例制导律作为比较对象：

(18)

(19)

其中： N1和N2为比例制导律系数， 在仿真中选取N1=5， N2=5。

本文提出的制导律式(9)和式(10)选取为

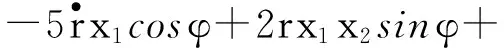
(20)

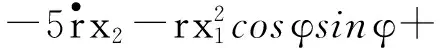
(21)

在仿真中， 假定目标机动方式为

aTθ=5g-10gsin(t)

(22)

aTφ=-5g+10gcos(t)

(23)

图2 视线倾角速率φ·输出曲线图3 视线偏角速率θ·输出曲线图4 视线倾角加速度指令aMφ输出曲线

图5 视线偏角加速度指令aMθ输出曲线图6 相对距离r输出曲线

仿真得到的脱靶量和拦截时间如表1所示。

表1　脱靶量与拦截时间

可以看出， 在两种制导律作用下导弹脱靶量均小于0.1m， 这说明导弹能够以直接撞击的方式命中目标。 从拦截时间上可以看出， 导弹在有限时间制导律的作用下， 能够以较短的时间命中目标， 而在比例制导律作用下， 需要更长的时间才能命中目标。

[1]RogersS.MissileGuidanceComparison[C]∥AIAAGuidance,Navigation,andControlConferenceandExhibit,Providence,RhodeIsland, 2004.

[2] 陈克俊, 赵汉元. 一种适用于攻击地面固定目标的最优再入机动制导律[J]. 宇航学报, 1994, 15(1): 1-7.

[3]YangCD,YangCC.AnalyticalSolutionofGeneralizedThree-DimensionalProportionalNavigation[J].JournalofGuidance,Control,andDynamics, 1996, 19(3): 721-724.

[4]SongSH,HaIJ.ALyapunov-LikeApproachtoPerformanceAnalysisof3-DimensionalPurePNGLaws[J].IEEETransactionsonAerospaceandElectronicSystems, 1994, 30(1): 238-248.

[5]OhJH,HaIJ.Capturabilityofthe3-DimensionalPurePNGLaw[J].IEEETransactionsonAerospaceandElectronicSystems, 1999, 35(2): 491-503.

[6]ChiouYC,KuoCY.GeometricApproachtoThree-DimensionalMissileGuidanceProblem[J].JournalofGuidance,Control,andDynamics, 1998, 21(2): 335-341.

[7] 韩大鹏, 孙未蒙, 郑志强, 等. 一种基于李群方法的新型三维制导律设计[J].航空学报, 2009, 30(3): 468-475.

[8] 周忠旺. 一种新型智能导引律及其仿真研究[J].航空兵器, 2011(2)： 12-16.

[9] 辛腾达， 范惠林， 闫琳. 滑模变结构制导律的抖振问题研究[J].航空兵器, 2015(2)： 10-13.

[10] 陈勃, 杨开红, 季海波．一种基于RBF神经网络增益调节的三维鲁棒导引律设计[J]．中国科学技术大学学报, 2015, 45(4): 280-285．

[11] 王祥, 方群. 一种基于θ-D次优控制的三维末制导律设计[J].西北工业大学学报, 2012, 30(2)： 196-200.

[12] 胡锡精, 黄雪梅. 具有碰撞角约束的三维圆轨迹制导律[J].航空学报, 2012, 33(3): 508-519.

[13]BhatSP,BernsteinDS.Finite-TimeStabilityofContinuousAutonomousSystems[J].SiamJournalonControlandOptimization, 2000, 38(3): 751-766.

Three-Dimensional Guidance Laws for Missile Based on Finite-Time Control Method

Li Younian1, Jiang Yun1, Li Shihua2, Zhang Zhenxing2

(1. China Airborne Missile Academy, Luoyang 471009, China; 2.Automation College, Southeast University, Nanjing 210096, China)

A new guidance law based on finite time feedback control method is proposed for the maneuvering target of three-dimensional missile interception. In this guidance law, the target acceleration is regarded as the external bounded disturbance of guidance system, and the switching function is introduced to restrain the disturbance of the system. By the theory analysis, it is proved that the line-of-sight angular rate can converge to zero in finite time.Numerical simulation results verify the effectiveness of this guidance law.

missile; target maneuver; three-dimensional guidance law; finite-time control

10.19297/j.cnki.41-1228/tj.2016.03.006

2015-07-30

航空科学基金项目(20130169002)

李友年(1964-)， 男， 山东日照人， 研究员， 研究方向为导弹控制系统设计。

TJ765.3

A

1673-5048(2016)03-0026-04