饱水裂隙破坏模式及影响因素理论分析

廖　斌, 黄厚旭, 戎晓力, 张志成

(中国人民解放军理工大学爆炸冲击防灾减灾国家重点实验室, 江苏 南京　210007)



饱水裂隙破坏模式及影响因素理论分析

廖斌, 黄厚旭, 戎晓力, 张志成

(中国人民解放军理工大学爆炸冲击防灾减灾国家重点实验室, 江苏 南京210007)

深长岩溶隧道掘进过程中掌子面和隧道两侧壁将出现大量裂隙，裂隙在远场应力与水压力的共同作用下将发生扩张膨胀，使得通过裂隙的水流量增大并最终导致隧道发生大范围的突水突泥事件。受水压致裂技术的影响，一般认为裂隙内部水流作用的机制是由水力劈裂和水压扩径造成的。基于断裂力学和流体力学，在平面受力情况下求解含水裂隙发生劈裂破坏和压剪破坏所需的临界水压值，并将两者进行比较后发现，同一裂隙发生水力劈裂破坏所需的临界水压大于其发生压剪破坏所需的临界水压，得出压剪破坏是含水裂隙破坏的主要形式。

岩溶隧道; 含水裂隙; 拉剪破坏; 压剪破坏; 破坏模式

0　引言

岩溶隧道突水突泥是近年来伴随着岩溶地区隧道大规模建设出现的工程问题，一旦发生大规模的突水，抽、排水几乎成为唯一的治理措施，但地下水的大量抽排会对当地生态环境造成毁灭性的破坏。为了保证隧道施工的安全，开展隧道突水突泥力学机制的研究显得尤为重要。目前国内外在隧道突水突泥机制方面的研究较少，已有的研究主要集中在岩溶地段施工工艺、灾害补救和不良地质的勘测上[1-3]；在防突措施上，以隔水岩板的厚度研究居多，文献[4-6]研究的成果虽然能在一定范围内解决工程问题，但是将开挖扰动后裂隙高度发育且不完整的岩石材料视为均质的隔水板与实际理论不符。

在扰动和卸荷作用的共同影响下，围岩中的原生裂隙将扩展，同时也会出现大量次生裂隙，裂隙在自身水压以及裂隙围压的共同作用下将从缓慢渗水发展到大量突水，这一过程经历了突水通道的形成和扩张，水流经历了从无到有、由小变大的过程。从表面上看，在这一过程中裂隙水对岩石起到劈裂的作用，而且水力劈裂早已广泛应用在石油工程中[7]，一些学者也做了相应的研究，如：徐幼平等[8]提出定向水力压裂技术并分析定向水力压裂过程中煤体的发展分布规律；门晓溪等[9]采用RFPA2D2.0-Flow软件，模拟分析了裂隙岩体在不同角度、不同长度、天然裂隙中，点与井孔之间不同间距的单一天然裂隙条件下的水压致裂过程；代树红等[10]研究了水力压裂作用下的层状岩体内的裂隙扩展特征；李利平等[11]对岩溶地区隧道裂隙水突出力学机制进行了研究。以上研究结果大多侧重于岩溶水对裂隙岩体的劈裂作用，且对于发生在岩溶隧道围岩内部的含水裂隙破坏机制多停留在水力劈裂层面，本文主要研究了不同条件下含水裂隙的主要破坏形式，并对不同破坏形式所需的条件进行了对比和分析。

1　裂隙中水压对裂隙的不利影响分析

对某铁路隧道现场的观测表明，掌子面突水往往是从量小到量大的非连续变化过程，爆破以及机械开挖的扰动使围岩内原生裂隙激活扩展并产生大量次生裂隙，由于岩溶岩体中含水丰富，所以胀开的裂隙中极易充水，如果将裂隙视为扁椭圆，根据裂隙的破坏方向(沿长轴或短轴)至少可以把裂隙的破坏方式划分为2种[12]：1)当裂隙沿短轴扩张，裂隙开度不断增大，储水能力不断加强，这种破坏可以归结为裂隙的拉剪破坏(即水力劈裂破坏)； 2)当裂隙周围压力变化使得裂隙含水，而此时的开度几乎不变，进而裂隙沿长轴发生滑移破坏，此时的破坏可归结为压剪破坏。这2种破坏是本文将要重点研究的2种情况。2种情况中裂隙水所起的作用并不相同，裂隙水最主要的作用是对裂隙内壁提供径向应力σw，当裂隙发生拉剪破坏时，该径向应力用于撑开和撕裂裂隙，而当压剪破坏出现时，该径向应力用于提供摩阻力-σwtanφ。根据摩尔-库仑准则可知，径向应力有利于减小压剪破坏过程中裂隙内面岩壁之间的摩阻力，加剧压剪破坏的发生。直观上看，此时的水体可看作是分布于裂隙内的润滑剂。从以上的分析可知，无论是拉剪破坏还是压剪破坏，裂隙内部水压都起到了重要的作用，并存在发生相应破坏的临界水压——拉剪破坏临界水压应力和压剪破坏临界水压应力。下文将建立相应的模型对这2种破坏方式进行计算分析，并确定含水裂隙破坏的主要形式。

1.1临界水压的确定

隧道掘进过程中掌子面和隧道侧壁面上裂隙的方向、大小和分布种类繁多，为了简化分析，本文只分析在掌子面和隧道侧壁面面内扩张并能贯通岩体的裂隙。由于此处只分析裂隙的扩张效应，不分析裂隙贯通掌子面的过程，而扩张效应可认为是发生在一个面内的，因此，可将问题简化为二维平面问题。岩溶隧道所受远场应力和隧道掌子面及侧壁面上含裂隙单元的受力如图1所示。

图1　开挖隧道掌子面和侧壁面含裂隙单元受力模型Fig. 1　Force model of fissure unit on tunnel face and tunnel sidewall

掌子面处充水裂隙受力模型如图2所示。图2中岩体单元含有一个长度为2c的扁椭圆形裂隙，裂隙的长轴方向与竖直方向之间的夹角为θ，裂隙中分布着均匀水压p，裂隙的远场应力分别为σx(水平方向)和σy(竖直方向)。根据断裂力学理论，可计算出此时裂隙内壁面上的应力状态为

(1)

式中σn、τ分别表示裂隙内面所受的正应力和切应力。

图2　掌子面处充水裂隙受力模型(掘进方向为z方向)Fig. 2　Force model of water-saturated fissure on tunnel face (boring along z-direction)

由于式(1)是完全依据断裂力学理论求出的结果，而断裂力学中规定拉应力为正、压应力为负，这与岩石力学中的规定截然相反，因此，将式(1)变换为

(2)

忽略开挖引起的掌子面上的应力集中，则隧道掌子面上的岩体单元所受应力满足

(3)

将式(3)代入式(2)可得

(4)

式中σn0、τ0为掌子面单元裂隙上的正应力和切应力。

如果裂隙处于隧道侧壁(如图3所示)，那么只需将式(2)中的竖向应力σy和水平应力σx分别以此时的环向应力σφ和轴向应力σz替代，即可得到此种情况下裂隙所受的正应力σnc0和切应力τc0，这样便可得到隧道侧壁含裂隙单元的受力，即

(5)

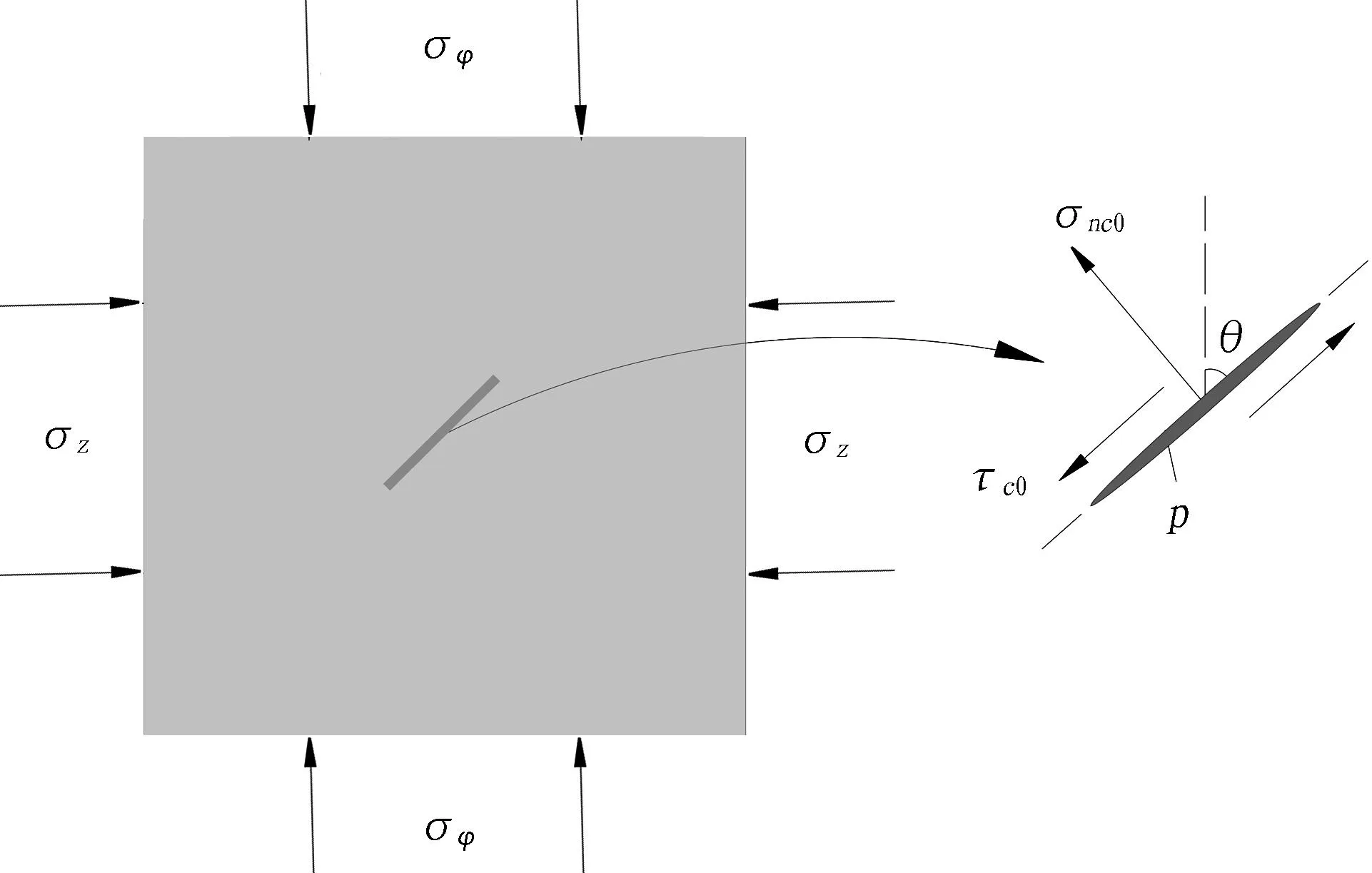
图3　隧道侧壁面裂隙单元受力模型

由于隧道掘进过程中与隧道轴线平行的轴向应力σz可认为基本不变，以下将根据平面受力问题，求出圆形隧道侧壁单元所受环向应力σφ，根据弹性理论可得

σφ=(p0/2){(1+λ)[1+(r/R)2]-(1-λ)[1+

3(r/R)4]cos 2β}。

(6)

式中：R为隧道半径；r为裂隙单元到隧道轴线的距离。

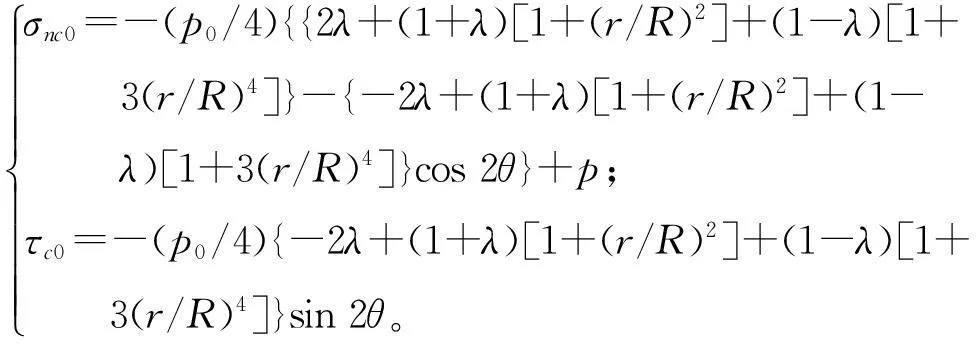
(7)

式中σnc0、τc0为隧道侧壁单元中裂隙的正应力和切应力。

由于裂隙受到沿其正向的张力和沿裂隙面的切向应力的共同作用，因此,此处裂隙的扩展可归结为Ⅰ、Ⅱ复合型裂隙问题，根据拉剪破坏准则[13-14]，

KⅠcc=KⅠ+KⅡ。

(8)

式中:KⅠcc为Ⅰ型断裂韧度，在特定的情况下可视为一个不变的常数；KⅠ、KⅡ分别为Ⅰ、Ⅱ型应力强度因子，且

(9)

1.2临界水压的求解

根据含裂隙单元所处位置的不同，临界水压的求解将分为2种情况。

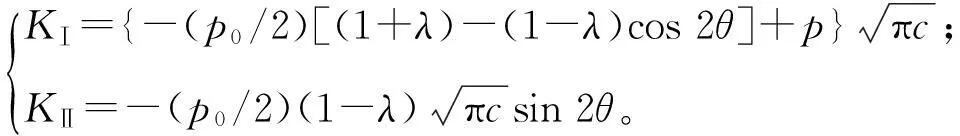
(10)

将式(10)代入式(8)可得到由裂隙内部水压作用导致裂隙拉剪破坏的临界水压

(11)

式(11)即是掌子面裂隙拉剪破坏时所需要的临界水压，该式表明裂隙的走向(θ)、远场应力(水平应力和垂直应力)以及裂隙扩展之前的原始长度(2c)都对裂隙发生拉剪破坏所需的临界水压pl1起到直接影响。

当裂隙在裂隙水压和远场应力共同作用下破坏时，裂隙将会发生沿裂隙长轴的剪切破坏，又称压剪破坏。压剪破坏时，裂隙水压的存在直接减小了相对滑移的两裂隙内壁面的正应力，进而导致裂隙之间的摩阻力减小，一般认为水体起到了润滑的作用。此时裂隙正向的有效剪应力

τeff=τ0-σn0tanφ0。

(12)

将式(4)代入式(12)可得

τeff=-(p0/2)(1-λ)sin 2θ+{(p0/2)[(1+λ)-

(1-λ)cos 2θ]-p}tanφ0。

(13)

由于此时的裂隙破坏属于压剪破坏，所以采用式(10)中的Ⅱ型应力强度因子进行计算

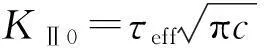
(14)

针对此种情况所使用的断裂准则为

KⅡcc=KⅡ0。

(15)

将式(13)代入式(14)，并结合式(15)，可得Ⅱ型断裂韧度

KⅡcc={-(p0/2)(1-λ)sin 2θ+{(p0/2)[(1+λ)-

(16)

根据式(8)和(10)可求出对应于压剪破坏时的临界水压

pl2=(p0/2)(1+λ)-(p0/2)(1-λ)(cos 2θ+

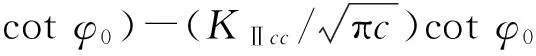
(17)

2)当裂隙处于隧道侧壁面上时，结合式(7)和式(9)可得此时的应力强度因子KsⅠ和KsⅡ为

(18)

将式(12)、(13)代入式(8)可得隧道侧面围岩拉剪破坏时的临界水压为

(1-λ)[1+3(r/R)4]}sin 2θ+(p0/4){{2λ+

(1+λ)[1+(r/R)2)]+(1-λ)[1+3(r/R)4]}-{-

2λ+(1+λ)[1+(r/R)2]+(1-λ)[1+3(r/R)4]}·

cos 2θ}。

(19)

根据式(12)可得隧道侧面围岩中裂隙两对面之间的有效剪切力

τseff=-(p0/4){-2λ+(1+λ)[1+(r/R)2]+(1-

λ)[1+3(r/R)4)]}sin 2θ+{(p0/4){{2λ+(1+

λ)[1+(r/R)2]+(1-λ)[1+3(r/R)4]}-{-2λ+

(1+λ)[1+(r/R)2]+(1-λ)[1+3(r/R)4]}·

cos 2θ}-p}tanφ0。

(20)

此时的断裂韧度可表示为

(21)

最终可求出隧道侧壁含裂隙单元的压剪破坏临界水压

psl2=(p0/4){{(1+λ)[1+(r/R)2]+(1-λ)[1+

3(r/R)4]+2λ}-{(1+λ)[1+(r/R)2]+(1-

λ)[1+3(r/R)4]-2λ}(cos 2θ+sin 2θ·

(22)

2　岩溶隧道裂隙破坏的主要影响因素分析

由上文隧道掌子面和隧道侧壁面的含水裂隙发生劈裂破坏和压剪破坏所需临界水压的表达式可以看出，侧压力系数λ、裂隙长度c、岩石内摩擦角φ0和裂隙走向θ都对发生相应破坏所需的临界应力具有明显的影响。为分析各因素的影响程度，下文将分情况进行研究。

2.1掌子面裂隙破坏的影响因素分析

根据文献[13]，锦屏某勘探隧道埋深2 848 m，附近实测隧道最大主应力为38.16 MPa，最小主应力为 14.81 MPa，大理岩I型裂隙断裂韧度为15.2 MN/m3/2，Ⅱ型裂隙断裂韧度为11.2 MN/m3/2。含水裂隙在隧道掌子面上时，为方便计算，取KⅠcc=15 MN/m3/2、KⅡcc=11MN/m3/2、p0=20 MPa、φ0=π/6。

2.1.1侧压力系数对掌子面上裂隙破坏的影响

(23)

由式(23)可得出掌子面上临界水压应力与侧压力系数的关系曲线，如图4所示。从图4可以看出：在其他条件限定的情况下，掌子面上裂隙发生压剪破坏所需的临界水压应力随着侧压力系数的增大而线性增长，在一定的侧压力系数范围内，压剪破坏所需的临界水压应力小于水力劈裂所需的临界水压应力。

2.1.2裂隙长度对掌子面上裂隙破坏的影响

当含水裂隙在隧道掌子面上时，取侧压力系数λ=1、裂隙长轴与竖向之间的夹角θ=π/4，根据式(11)和(17)可得

(24)

由式(24)可得出掌子面上临界水压应力与裂隙长度的关系曲线，如图5所示。从图5可以看出：在裂隙长度逐渐增加的过程中，水力劈裂所需的临界水压应力减小，而压剪破坏所需的临界水压应力增大，这可能是由于裂隙长度增大导致裂隙间滑动时彼此的接触面积增大，因此，就需要更大的水压应力来支撑裂隙间的相互滑动面，使得压剪错动更容易实现。当裂隙半长c在1.5 m以下时，随着裂隙长度的增加，发生2种破坏的临界水压应力随着裂隙长度的增长变化明显；当裂隙半长c超过1.5 m后，裂隙长度的变化对裂隙发生2种破坏所需的临界水压应力的影响减小。据此可得出发生劈裂破坏所需的临界水压应力大于压剪破坏所需的临界水压应力。

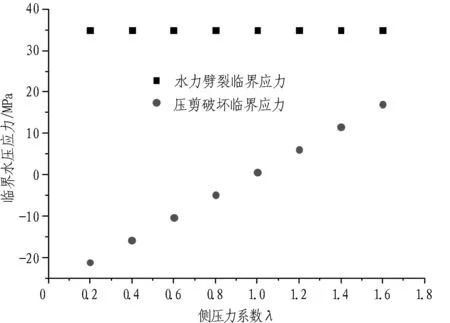
图4　掌子面上临界水压应力与侧压力系数的关系曲线图

Fig. 4Critical water pressure stress vs. lateral pressure coefficient on tunnel face

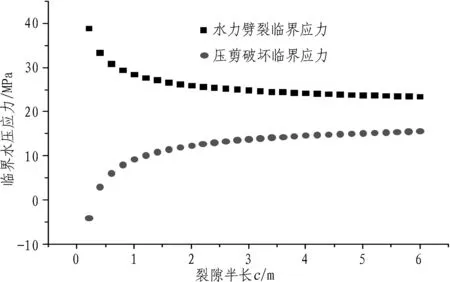
图5　掌子面上临界水压应力与裂隙长度的关系曲线图

Fig. 5Critical water pressure stress on tunnel face vs. fissure length

2.1.3裂隙走向对掌子面上裂隙破坏的影响

(25)

由式(25)可得出掌子面上临界水压应力与裂隙走向的关系曲线，如图6所示。从图6可以看出：掌子面裂隙受裂隙走向的影响不大，但裂隙发生压剪破坏的临界水压应力仍然小于裂隙发生水力劈裂破坏所需的临界水压应力。

图6　掌子面上临界水压应力与裂隙走向的关系曲线图Fig. 6　Critical water pressure stress on tunnel face vs. fissure direction

2.2隧道侧壁面上裂隙破坏的影响因素分析

当含水裂隙在隧道侧壁上时，为方便计算，取KⅠcc=15 MN/m3/2、KⅡcc=11 MN/m3/2、p0=20 MPa、

φ0=π/6。

2.2.1侧压力系数对隧道侧壁面上裂隙破坏的影响

(26)

由式(26)可得隧道侧壁面上的临界水压应力与侧压力系数的关系曲线，如图7所示。从图7可以看出: 随着侧压力系数的增大，裂隙发生水力劈裂所需的水压应力减小，而发生压剪破坏所需的临界水压应力增大，但整体上发生水力劈裂的临界水压应力大于发生压剪破坏所需的临界水压应力。

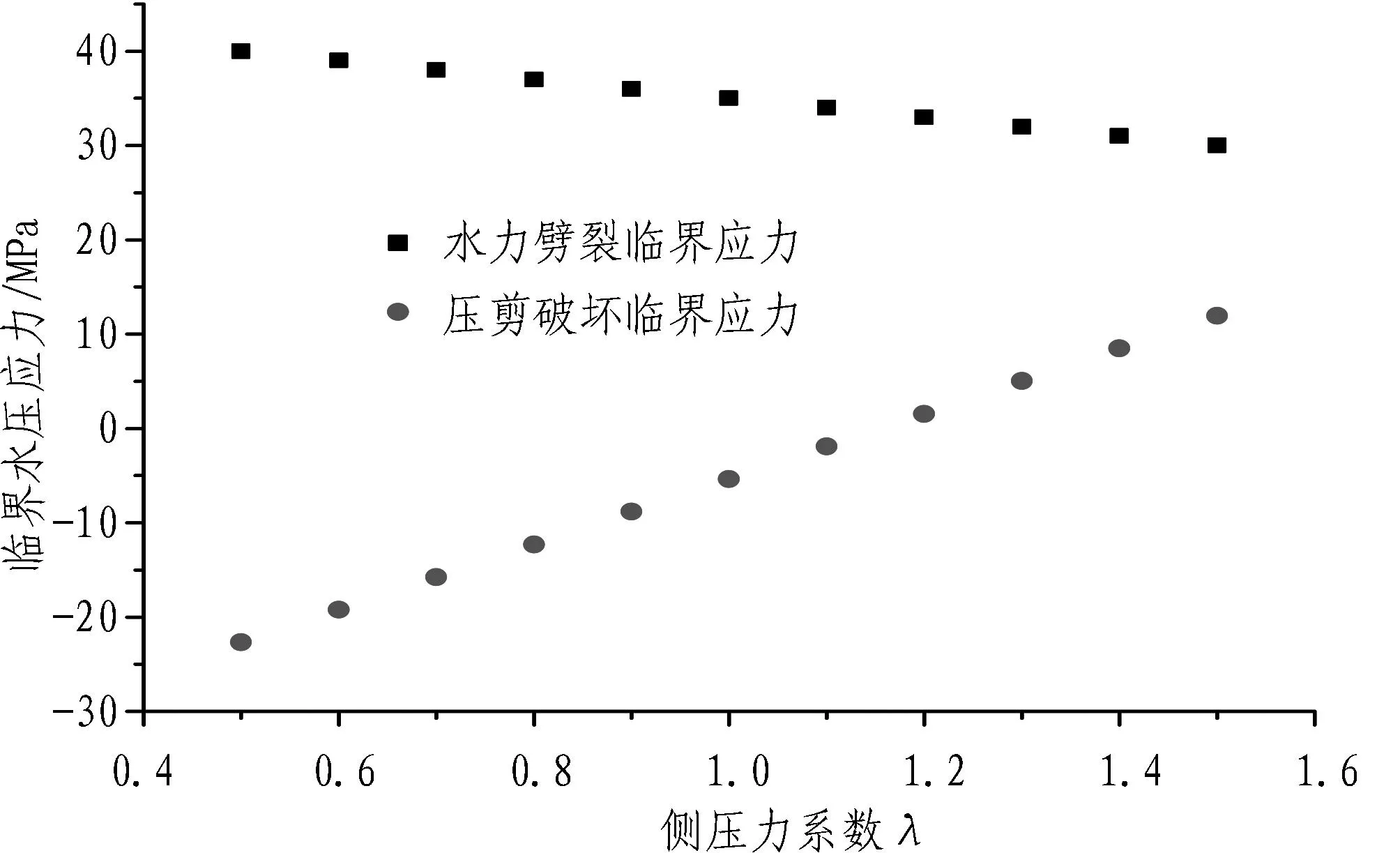
图7　隧道侧壁面上的临界水压应力与侧压力系数的关系曲线图Fig. 7　Critical water pressure stress vs. lateral pressure coefficient on tunnel sidewall

2.2.2裂隙长度对隧道侧壁面上裂隙破坏的影响

取侧压力系数λ=1、隧道轴线相对距离r/R=1、裂隙长轴与竖向之间的夹角θ=π/4，根据式(19)和(22)可得

(27)

由式(27)可得隧道侧壁面上的临界水压应力与裂隙长度的关系曲线，如图8所示。从图8可以看出：随着裂隙长度的增大，裂缝发生水力劈裂所需的临界水压应力减小，而发生压剪破坏的临界水压应力增大，并且当裂隙长度较短时，裂隙长度的改变对裂隙发生2种破坏所需的临界应力影响明显，而裂隙半长超过1.5 m后这种影响将不再明显，这与 2.1.2中得出的结论一致，且整体上发生水力劈裂所需的临界水压应力大于发生压剪破坏所需的临界水压应力。

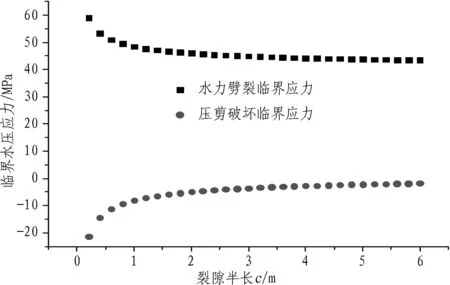
图8　隧道侧壁面上的临界水压应力与裂隙长度的关系曲线图

Fig. 8Critical water pressure stress on tunnel sidewall vs. fissure length

2.2.3裂隙走向对隧道侧壁面上裂隙破坏的影响

(28)

由式(28)可得隧道侧壁面上的临界水压应力与裂隙走向的关系曲线，如图9所示。从图9可以看出：在一定范围内，裂隙长轴与竖向之间夹角的变化对裂隙发生2种破坏所需临界水压的影响均非常明显，同样可以得出发生水力劈裂所需的临界水压应力在一定范围内大于发生压剪破坏所需的临界水压应力。

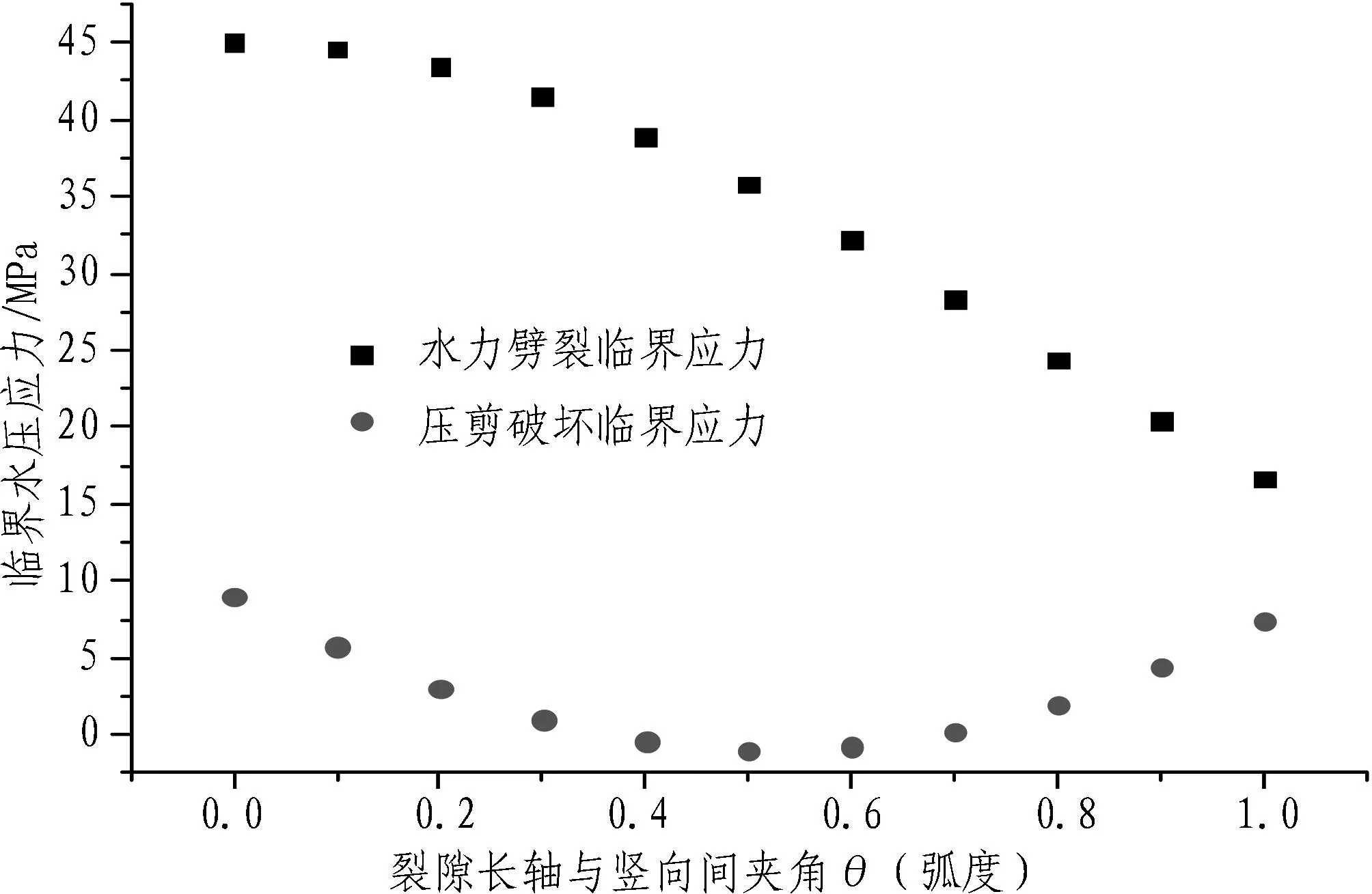
图9　隧道侧壁面上的临界水压应力与裂隙走向的关系曲线图

Fig. 9Critical water pressure stress on tunnel sidewall vs. fissure direction

2.2.4隧道轴线相对距离对隧道侧壁面上裂隙破坏的影响

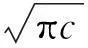
(29)

由式(29)可得隧道侧壁面上的临界水压应力与隧道轴线相对距离的关系曲线，如图10所示。从图10可以看出：当裂隙所在平面距隧道轴线的相对距离增大时，裂隙发生劈裂破坏所需的临界应力和发生压剪破坏所需的临界应力都相应增大，但是考虑到一般隧道半径都在5 m以上，因此，只分析离隧道边沿4 m范围以内的平面上裂隙的破坏形式即可，在这个范围内，即r/R≥1.6时，裂隙发生水力劈裂破坏所需的临界水压应力大于发生压剪破坏所需的临界水压应力这一结论也是成立的。

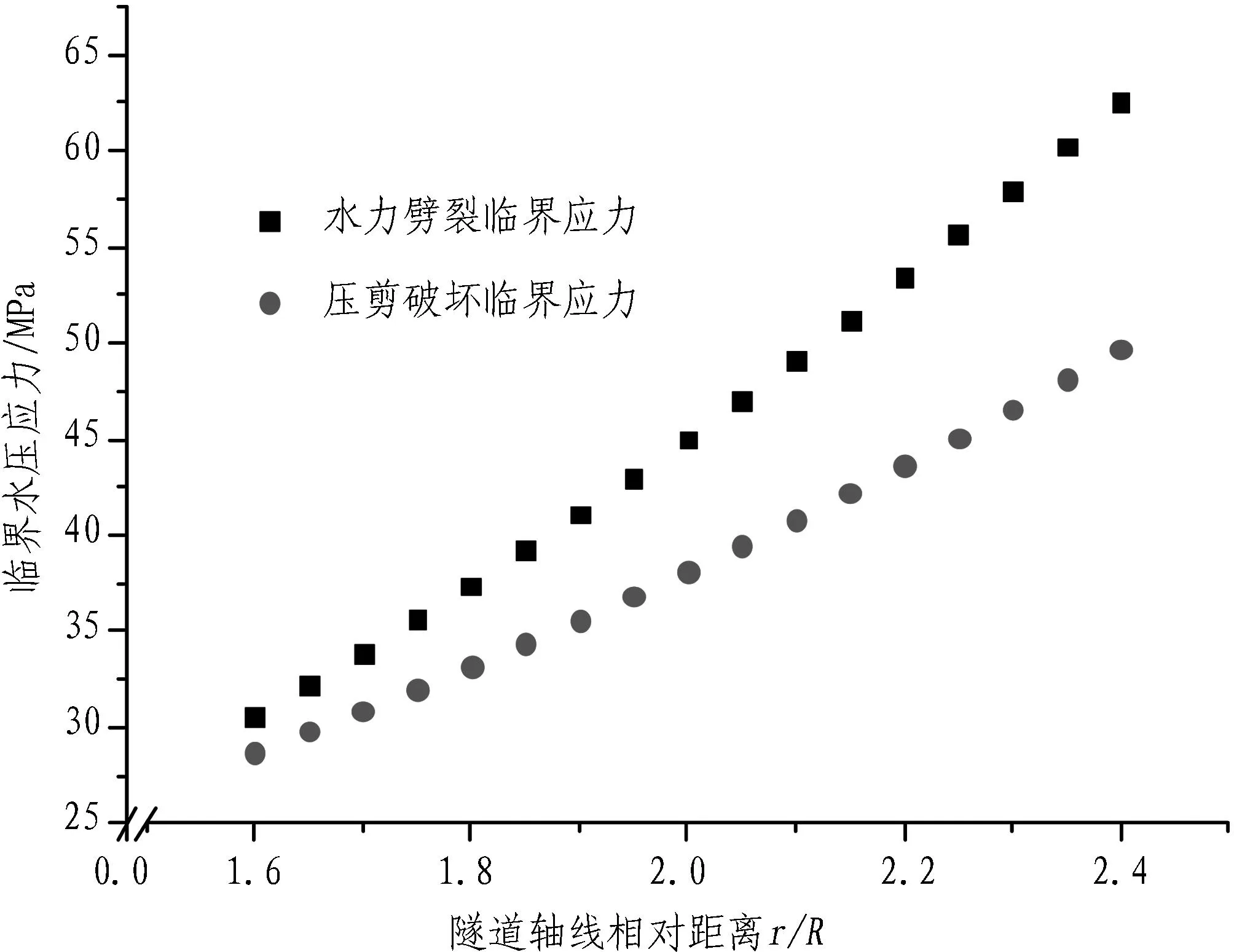
图10隧道侧壁面上的临界水压应力与隧道轴线相对距离r/R的关系曲线图

Fig. 10Critical water pressure stress on tunnel sidewall vs. relative distance of tunnel axial line (r/R)

3　结论与建议

文章将掌子面含水裂隙简化后，运用断裂力学原理，结合岩石力学理论推导出含水裂隙掌子面及其侧壁面发生拉剪破坏和压剪破坏的2种临界水压应力表达式，根据文献[13]给出的现场实测值进行讨论分析，结果表明：处于掌子面上的含水裂隙发生拉剪破坏所需的临界水压应力大于压剪破坏所需的临界水压应力，而处在侧壁面上的含水裂隙，在工程实际容许的范围内，含水裂隙发生拉剪破坏所需的临界水压应力仍大于压剪破坏所需的临界水压应力。这说明，隧道围岩在实际开挖过程中，含水裂隙发生破坏的主要形式是压剪破坏。本文研究表明：含水裂隙的增长扩径并不是由水力劈裂导致的，这与传统的认识有所不同。

在隧道开挖过程中，对于开挖和施工扰动如何使含水裂隙扩径以及隧道由少量渗水直到大量突水失稳这一过程的机制需要进行更加深入的研究。目前对隧道突水突泥的研究大多数停留在理论方面，应加强理论与实践的结合，不断充实完善理论，为指导安全施工创造良好的条件。

[1]刘招伟，何满潮，王树仁.圆梁山隧道岩溶突水机理及防治对策研究[J].岩土力学，2006,27(2)：228-232.(LIU Zhaowei, HE Manchao, WANG Shuren. Study of karst waterburst mechanism and prevention countermeasures in Yuanliangshan Tunnel [J].Rock and Soil Mechanics, 2006, 27(2): 228-232. (in Chinese))

[2]周宗青，李术才，李利平,等.特长深埋隧道基岩裂隙水探测与应用研究[J].地下空间与工程学报，2012,8(1)：99-105.(ZHOU Zongqing, LI Shucai, LI Liping, et al. Detection of bedrock fissure water and its application in extra long and deep tunnel engineering[J].Chinese Journal of Underground Space and Engineering,2012,8(1): 99-105.(in Chinese))

[3]郭佳奇，李宏飞，徐子龙.岩溶区隧道突水灾害防治原则及治理对策[J].中国地质灾害与防治学报,2014,25(3)：56-62. (GUO Jiaqi, LI Hongfei, XU Zilong. Prevention principles and treating techniques of water inrush in karst tunnel [J]. The Chinese Journal of Geological Hazard and Control, 2014, 25(3): 56-62. (in Chinese))

[4]干昆蓉，杨毅，李建设.某隧道岩溶突水机理及安全岩墙厚度的确定[J].隧道建设，2007,27(3)：13-16. (GAN Kunrong, YANG Yi, LI Jianshe. Analysis of karst water inflow mechanisms and determination of thickness of safe rock walls: Case study of a tunnel[J]. Tunnel Construction, 2007, 27(3): 13-16. (in Chinese))

[5]孙谋，刘维宁.高风险岩溶隧道掌子面突水机制研究[J].岩土力学，2011,32(4): 1175-1180. (SUN Mou, LIU Weining. Research on water inrush mechanism induced by karst tunnel face with high risk [J]. Rock and Soil Mechanics, 2011,32(4): 1175-1180. (in Chinese))

[6]李集，卢浩，夏沅谱. 岩溶隧道防突安全厚度研究综述及估算方法探讨[J].隧道建设，2014,34(9)：863-873. (LI Ji, LU Hao, XIA Yuanpu. Survey and research on estimation method of against-inrush safe thickness of rock strata in karst tunnels [J].Tunnel Construction,2014,34(9): 863-873.(in Chinese))

[7]盛金昌， 赵坚，速宝玉.高水头作用下水工压力隧道的水力劈裂分析[J].岩石力学与工程学报，2005,24(7)：1226-1230. (SHENG Jinchang, ZHAO Jian, SU Baoyu. Analysis of hydraulic fracturing in hydraulics tunnels under high water pressure [J].Chinese Journal of Rock Mechanics and Engineering，2005, 24(7): 1226-1230. (in Chinese))

[8]徐幼平,林柏泉，翟成,等. 定向水力压裂裂隙扩展动态特征分析及其应用[J].中国安全科学学报，2011,21(7): 104-111.(XU Youping， LIN Baiquan， ZHAI Cheng, et al. Analysis of dynamic characteristics of cracks extension in directional hydraulic fracturing and its application[J]. China Safety Science Journal,2011,21(7): 104-111.(in Chinese))

[9]门晓溪,唐春安，李宏,等. 单裂隙岩体水力裂缝扩展机理的数值模拟[J].应用力学学报，2014,31(2): 261-265. (MEN Xiaoxi, TANG Chun’an, LI Hong, et al. Numerical simulation on propagation mechanism of hydraulic fracture on fractured rockmass[J].Chinese Journal of Applied Mechanics,2014,31(2): 261-265.(in Chinese))

[10]代树红,王召，潘一山,等. 水力压裂作用下裂隙在层状岩体内的扩展特征[J].地球物理学进展，2014,29(5)：2370-2375.(DAI Shuhong，WANG Zhao，PAN Yishan，et al. Study of characteristics of crack propagation in stratified rock under the force of hydraulic fracturing[J].Progress in Geophysics,2014,29(5): 2370-2375.(in Chinese))

[11]李利平，李术才，张庆松. 岩溶地区隧道裂隙水突出力学机制研究[J].岩土力学，2010,31(2)：523-528. (LI Liping, LI Shucai, ZHANG Qingsong. Study of mechanism of water inrush induced by hydraulic fracturing in karst tunnels[J].Rock and Soil Mechanics, 2010,31(2)：523-528.(in Chinese))

[12]王建秀，朱合华，唐益群，等.石灰岩损伤演化的断裂力学模型及耦合方程[J].同济大学学报(自然科学版)，2004,32(10)：1320-1324.(WANG Jianxiu, ZHU Hehua, TANG Yiqun, et al. Fracture mechanical model and hydrochemical-hydraulic coupled damage evolution equation of limestone [J]. Journal of Tongji University(Natural Science), 2004, 32(10): 1320-1324. (in Chinese))

[13]黄润秋，王贤能，陈龙生.深埋隧道涌水过程的水力破裂作用分析[J].岩石力学与工程学报，2000,19(5)：573-576.(HUANG Runqiu ,WANG Xianneng, CHEN Longsheng. Hydro-splitting off analysis on underground water in deep-lying tunnels and its effect on water gushing out[J]. Chinese Journal of Rock Mechanics and Engineering, 2000,19(5)：573-576. (in Chinese))

[14]李宗利.岩体水力劈裂机理研究及其在地下洞室围岩稳定分析中应用[D]．南京：河海大学,2005.(LI Zongli.Study of rock hydraulic fracturing mechanism and application to rock stability analysis of tunnel surrounding[D].Nanjing: Hohai University,2005.(in Chinese))

[15]洪开荣. 我国隧道及地下工程发展现状与展望[J].隧道建设，2015，35(2)：95-107. (HONG Kairong. State-of-art and prospect of tunnels and underground works in China[J].Tunnel Construction,2015,35(2): 95-107.(in Chinese))

Theoretical Analysis of Failure Mode of Water-saturated Fissure and Its Influencing Factors

LIAO Bin, HUANG Houxu, RONG Xiaoli, ZHANG Zhicheng

(StateKeyLaboratoryofExplosion&ImpactandDisasterPrevention&Mitigation,PLAUniversityofScienceandTechnology,Nanjing210007,Jiangsu,China)

A large amount of fissures would occur on tunnel face and tunnel sidewalls during deep long karst tunnel excavation. Due to the interaction of far-field stress and water pressure, the fissures would be expanded and the water flow rate will be increased. As a result, large-scale water and mud gushing would occur.The mechanism of internal water effect of fissures is considered to be hydraulic fracture effect and hydrostatic expansion effect popularly. The critical water pressure stresses of tenso-shear failure and compression-shear failure in conditions of plane strain are calculated based on fracture mechanics and fluid mechanics. The calculated results show that the critical water pressure stress of tenso-shear failure is larger than that of compression-shear failure. The compression-shear failure is the main failure mode of water-saturated fissure.

karst tunnel; water-saturated fissure; tenso-shear failure; compression-shear failure; failure mode

2015-12-17；

2016-03-31

国家重点基础研究发展计划“973”项目(2013CB036005)

廖斌(1990—)，男，宁夏石嘴山人，中国人民解放军理工大学建筑与土木工程专业在读硕士，研究方向为地下工程安全风险管理。E-mail：l_bin90@163.com。

10.3973/j.issn.1672-741X.2016.08.007

U 45

A

1672-741X(2016)08-0933-08