东胜煤田新街矿区斜井保护煤柱设计的离散元分析

杨　旭， 项彦勇

(1. 北京交通大学土木建筑工程学院， 北京　100044； 2. 中铁第五勘察设计院集团有限公司， 北京　102600)



东胜煤田新街矿区斜井保护煤柱设计的离散元分析

杨旭1,2， 项彦勇1

(1. 北京交通大学土木建筑工程学院， 北京100044； 2. 中铁第五勘察设计院集团有限公司， 北京102600)

为了最大限度进行煤层开采并控制其对斜井结构的不利影响，需要估算合理的斜井保护煤柱尺寸。针对地层-斜井的5个不同横截面，采用经验公式法估算煤柱尺寸，并进行二维离散元数值模拟，分析斜井管片结构内力和位移的分布特征，并给出合理的煤柱尺寸。主要结论如下：1)根据二维离散元数值模拟得到的煤柱尺寸小于根据经验公式得到的煤柱尺寸；2)随着回采工作面与斜井水平距离的减小，斜井结构首先轻微上浮，然后显著下沉；3)当斜井与开采煤层的竖向距离较小时，斜井结构因受到破裂岩层的下沉挤压作用而向远离开采工作面的方向变位；4)当斜井与开采煤层的竖向距离足够大时，斜井向开采工作面的方向变位；5)由于斜井穿越的岩层与煤层物理力学性质的差异，在不同岩层或煤层之间的交界面附近，斜井结构可能因应力集中而承载力不足，需要采取一定的改善与控制措施。

煤层； 斜井； 管片； 煤柱尺寸； 经验公式法； 离散元数值模拟

0　引言

煤层开采过程中破坏了原岩应力场的平衡状态，会引起围岩应力的重分布[1]。由于煤矿地下开采范围大、层数多而开采深度有限，影响一般都能发展到地表，波及上覆岩层与地表的一些与人类生产和生活密切相关的对象，如湖泊、铁路和建(构)筑物等[2]。谢广祥等[3]采用计算机数值模拟结合现场实测研究的方法, 揭示了煤柱宽度变化对综放面围岩应力分布及变化规律的影响，煤柱宽度的变化会使煤柱内与相邻工作面煤体内应力分布规律不同。李学华等[4]针对泉沟煤矿-115大巷下压煤情况进行模拟分析，认为下伏开采煤层和大巷之间的距离是影响围岩稳定性的重要因素。以上研究均表明，保留足够尺寸的煤柱是减小或避免煤层开采对邻近建(构)筑物产生不利影响的有效措施。

针对保护煤柱的留设问题，传统煤柱留设有相应的经验公式，经验公式只笼统地涉及煤层的几何参数和力学性质，但是保护煤柱尺寸与开采深度、开采厚度并非传统认为的简单线性关系，而是呈现出复杂的非线性关系[5]，并且经验公式认为移动角是一个定值, 这不符合深部开采条件下的岩层移动规律[6]。煤层埋藏深度、煤层厚度、煤层倾角、煤的硬度、巷道断面大小和支护阻力等都是影响保护煤柱宽度留设的主要因素[7]，数值模拟方法可以综合考虑这些因素，弥补经验公式的不足。本文采用经验公式与二维离散元数值模拟相结合的方法，以神华集团东胜煤田新街矿区煤层的开采设计问题为背景，研究了斜井位移及管片稳定性与斜井层位及保护煤柱宽度的关系，以最大限度地进行煤层开采并控制其对斜井结构的不利影响为原则，计算得出岩层破裂角，并经过对比分析，提出建议的煤柱尺寸。

1　矿区概况与计算截面选择

如图1所示，矿区含有5个煤组共计17个煤层，其中，煤层2-2上、2-2、3-1、5-1、6-1、6-2和6-3共7层为大部可采，2-1上、2-1、4-1、5-2和5-3共5层为局部可采，2-2下、3-1下、3-2、4-2和6-2下为不可采煤层。各个煤层的倾角都很小，近似为水平分布。按照开采规划，首先开采厚度2.4 m的3-1煤层。

用于运输的主、副斜井采用TBM工法施工(在煤炭行业尚属首次)，每个井筒的斜长为6 558 m，倾角为6°，落底于3-1煤层底板，地面标高+1 322 m，落底标高+636 m，提升高差686 m，底部与井田中部大巷相连，主、副斜井中心之间的水平距离为60 m。

矿区的地质构成主要包括侏罗系、白垩系、第三系上新统和第四系更新统、全新统，以侏罗系为主，其中，直罗组与安定组主要为砂质泥岩、中细粒砂岩与泥岩互层、粗粒砂岩及局部夹泥岩。3-1煤层顶板多为粉砂岩及砂质泥岩，局部为中粒砂岩，底板多为砂质泥岩和泥岩。

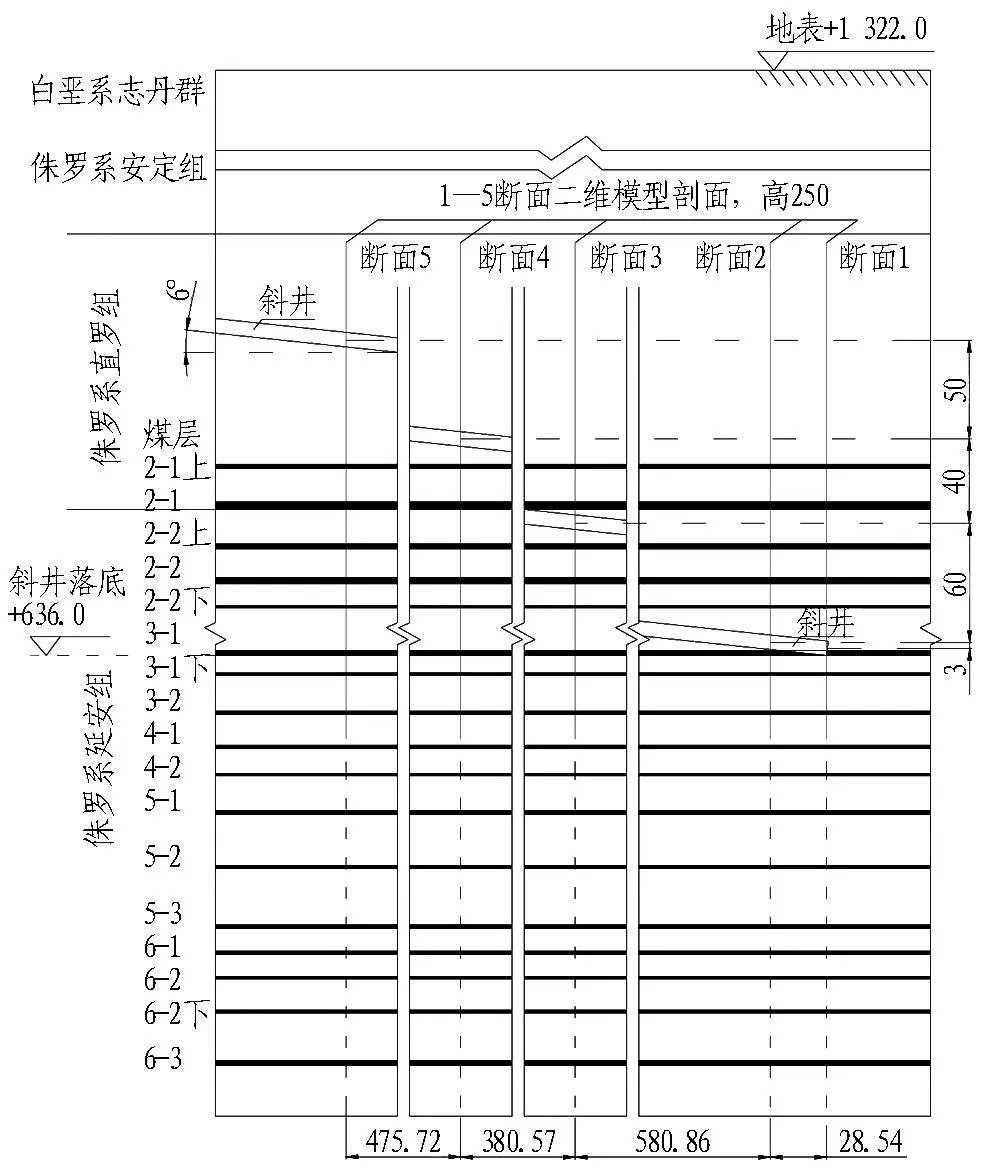
图1　矿区岩层、煤层、斜井和计算断面(单位：m)

2　煤柱尺寸的经验公式法估算

对位于单个煤层内或多个煤层最上方煤层内的斜井或巷道，在两侧的煤层及其下方各个煤层中都应该留有一定尺寸的煤柱，以保护斜井或巷道的安全和稳定。如图2(a)所示，a为受护斜井或巷道宽度的一半，经验公式[8]为

(1)

如图2(b)所示，当斜井或巷道位于开采煤层上方时，从斜井或巷道所在煤层的煤柱边界起，以地层移动角δ为边界在下方煤层中保留煤柱。

如图3所示，对于本矿区的3-1煤层和斜井，可有

L=(h-h1)cotθ;

(2)

S2=hcotδ+S1;

(3)

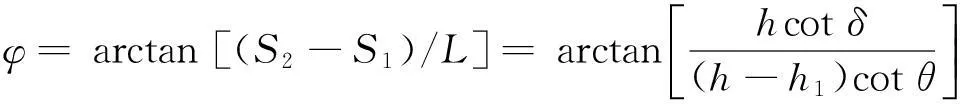
(4)

式(2)—(4)中：h为任意断面处斜井中心与煤层顶面之间的(垂直)距离，m；h1为落底断面处斜井中心与煤层顶面之间的距离，m；L为任意断面与落底断面之间的水平距离，m；θ为斜井的倾角;S2为与煤层顶面垂直距离为h的断面处的煤柱宽度,m；δ为断面内的移动角；φ为斜井保护煤柱边线与斜井轴线在水平面上投影的夹角。

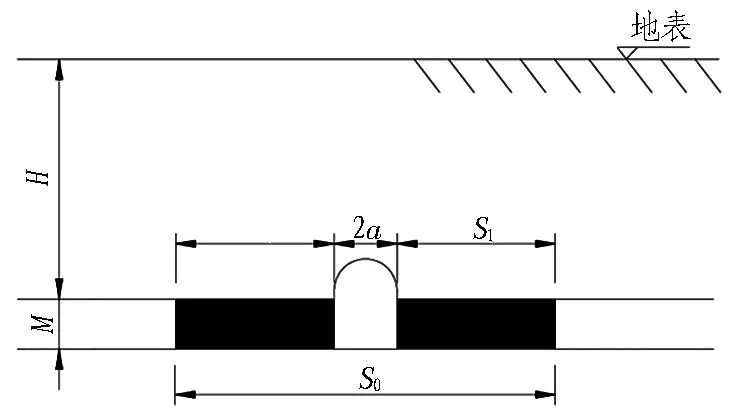
(a)

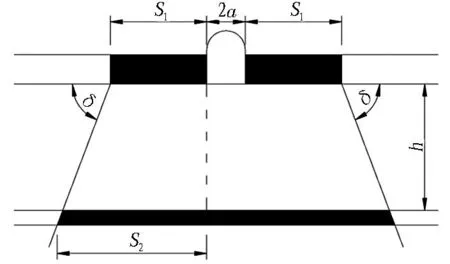
(b)

Fig. 2Concept model of empirical formula method to calculate protective coal pillar dimensions[8]

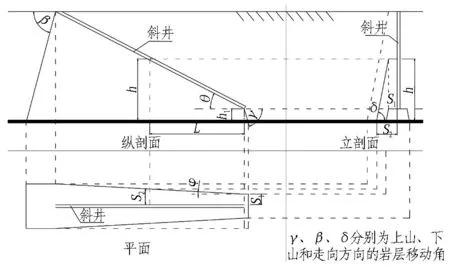
图3　斜井保护煤柱尺寸的经验公式法估算

Fig. 3Empirical formula method to calculate protective coal pillar dimensions

当30≤Rc≤60时，地层移动角δ、γ、β之间有如下经验关系[8]

(5)

式中:α为煤层的倾角；Rc为岩层的单向抗压强度，MPa。根据文献[1]可知，当α<5°时，δ=γ=β。

对于本矿区的3-1煤层和斜井底部断面，M=2.4 m，H=686 m，Rc=26 MPa，由式(1)计算可得保护煤柱宽度S1=41 m。

对于本矿区的3-1煤层和与煤层顶面垂直距离为h的断面，α=0°，θ=6°，h1=0，安定组、直罗组与延安组的单向抗压强度分别为32.66、34.62、40.11 MPa，根据式(5)插值可得地层移动角δ、γ、β分别为70.44°、70.77°、71.69°，取δ=γ=β=71°，再结合几何关系，由式(2)—(4)可得,φ=2.06°，S2=hcotδ+S1=0.344h+41。

3　煤柱尺寸的二维离散元计算分析

3.1模型与参数

针对任意一个斜井，选取二维离散元的断面模拟范围如图4所示，右边界为2个斜井之间的中分线(对称线)，距离模拟斜井中心的水平距离为30 m。斜井采用C40钢筋混凝土管片结构，外直径为7.3 m，厚度为0.35 m。如图1所示，为了考虑不同断面处3-1煤层与斜井的不同相对位置，选取5个断面，分别进行二维离散元数值模拟，断面1位于斜井落底处，断面2、3、4、5分别位于断面1上方3、60、100、150 m处。将模拟范围上方的岩层重力转换为均匀分布的压力，施加在模型的上表面，集度为11.07 MPa。模拟范围的岩层简化为厚135.6 m的侏罗系直罗组及114.4 m的侏罗系延安组。勘探资料给出的岩石力学参数见表1。

图4二维离散元当数值模拟范围(含5个不同的斜井断面)及 3-1煤层开采范围(单位：m)

Fig. 4Scope of 2D discrete element analysis and mining area of coal seam 3-1 (m)

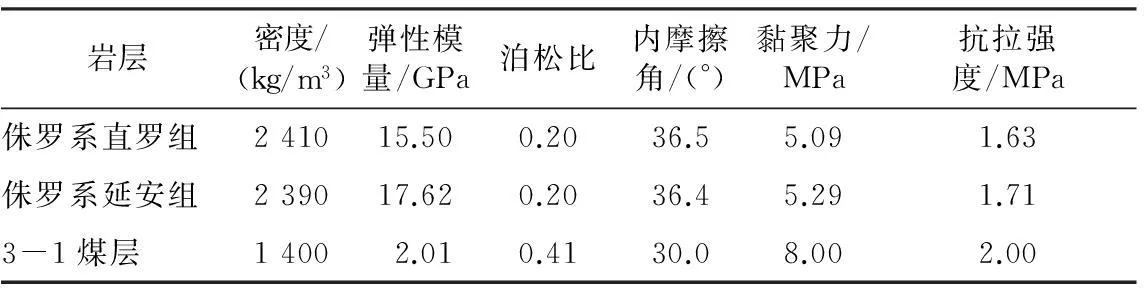
表1　岩石的力学参数

关于节理的物理力学参数，文献 [9-11]探讨了节理刚度参数的估算方法。在UDEC软件中，对节理刚度可按式(6)估算[12]

(6)

式中：kn和ks为节理的法向和切向刚度；Er和Em为岩块和岩体的弹性模量；Gr和Gm为岩块和岩体的剪切模量；D为节理间距。

岩体的强度由完整岩石和节理共同决定，令θ1和θ2为等效岩体由节理控制的最大和最小破裂角，θ为节理面与最大主平面的夹角，则节理岩体的等效强度参数可表达如下[13-14]：

当θ<θ1或θ>θ2时，

(7)

当θ1<θ<θ2时，

(8)

式中：φm和φr分别为节理岩体和完整岩石的内摩擦角；Cm和Cr分别为节理岩体和完整岩石的黏聚力;Cj和φj分别为节理的黏聚力与摩擦角。由式(8)可以解出节理的黏聚力与摩擦角。

根据相关文献和资料估算，采用的节理力学参数如表2所示。

表2　节理力学参数

3.2计算结果与分析

3.2.1斜井管片结构内力计算结果与分析

当3-1煤层开采后，顶板自由下沉垮落，围岩受到扰动，随着回采工作面与斜井结构邻近外缘之间距离逐渐减小，斜井管片结构最不利断面处的轴力和弯矩分别如图5和图6所示。由图5和图6可知，轴力随着回采工作面与斜井距离的减小而逐渐增大，弯矩先减小后增大；随着斜井与3-1煤层之间竖向距离的增大，轴力与弯矩逐渐减小。按钢筋混凝土矩形断面偏心受压构件[15]计算，可得斜井管片结构的安全系数。如图7所示，随着回采工作面与斜井距离的减小，安全系数先是基本不变，然后逐渐减小；安全系数随斜井与3-1煤层之间竖向距离的增大而增大。

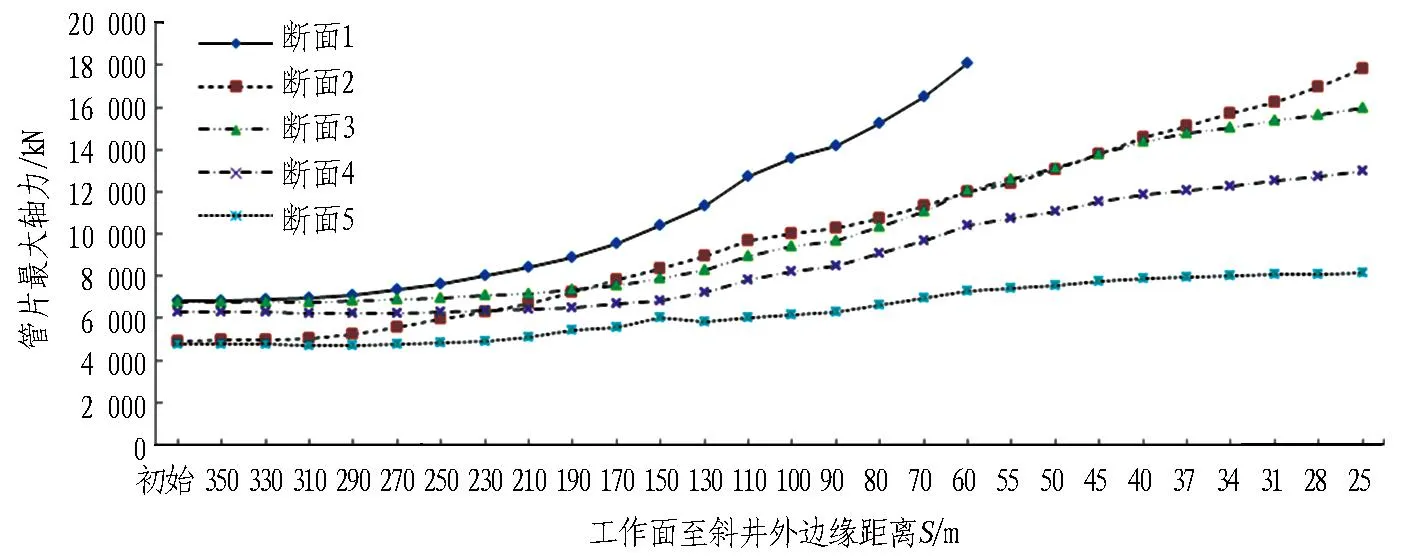
图5　斜井管片结构轴力

图6　斜井管片结构弯矩

图7　斜井管片结构最不利断面的安全系数

假如仅从斜井管片结构承载力角度考虑，断面1、2、3、4、5的保护煤柱宽度应该分别不大于110、40、37、25、25 m。对于斜井落底处的断面1，由于斜井穿越3-1煤层与侏罗系延安组岩层的分界面，如图8所示，由于应力集中，管片的内力最为不利(显著大于其他几个断面)，安全系数最小。

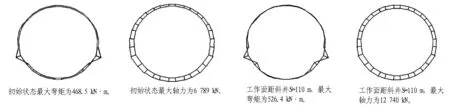
(a)(b)(c)(d)

图8斜井管片结构在断面1处的初始内力和工作面与斜井距离为110 m时的内力

Fig. 8Axial forces and bending moments of inclined shaft structure at cross-section 1 and those when distance between working face and inclined shaft of 110 m

3.2.2斜井管片结构变位计算结果与分析

如图9和图10所示(图9的平均位移是指管片节点位移的平均值)，随着回采工作面与斜井水平距离的减小，斜井结构先轻微上升，然后下沉；并且，除断面1以外，从断面2至断面5，斜井结构的竖向位移随斜井与3-1煤层之间竖向距离的增大而增大(伴随采空区上方内侧地层的下沉，回采初期当采空区距离较远时，斜井结构因采空区上方内侧-外侧地层的“杠杆”内沉外升作用而上升；回采中后期当采空区距离较近时，斜井结构因采空区上方内侧-外侧地层的携带下沉作用而下沉)。当斜井结构与开采煤层的竖向距离较小时，斜井结构因受到破裂岩层的下沉挤压作用而向远离回采工作面的方向变位；当斜井结构与开采煤层的竖向距离足够大时，斜井结构向回采工作面的方向变位。

对于回采工作面与斜井结构之间的不同水平距离(不同煤柱宽度)，以断面2为例，斜井结构的变位特点如图11所示。

3.2.3基于离散元计算分析的保护煤柱尺寸

保护煤柱的尺寸必须保证煤层开采不会对斜井结构的承载安全性和变位稳定性造成不可接受的影响。基于上面的离散元计算分析可知，由于煤层开采的影响，斜井结构在落底断面附近的变位虽然较小但内力结构却较为不利，保护煤柱尺寸的选择应该主要根据该断面的承载安全性决定；随着斜井结构与开采煤层之间竖向距离的增大，斜井结构断面内力的增量虽然减小，但变位却更为不利，保护煤柱尺寸的选择应该主要根据该断面的变位稳定性决定。

基于离散元计算分析和上述原则，斜井结构在断面1、2处的煤柱宽度由承载安全性决定，分别取110、40 m；在断面3、4、5处由变位稳定性决定，按关系式S1+hcotδ取值，其中，S1=40 m为断面2处的煤柱宽度，h分别代表断面3、4、5处斜井结构外缘与3-1煤层顶面之间的最小竖向距离(已知)，δ分别代表针对断面3、4、5选取的岩层移动角(如图12所示，当岩层破裂线与斜井结构外缘之间的最小水平距离最接近S1时的岩层破裂角)。断面3、4、5处煤柱宽度的另一种算法是：以断面3为例，在离散元计算结果中，当回采工作面与斜井结构边缘之间的水平距离为55 m时，岩层破裂线与斜井结构外缘之间的最小水平距离为 39.25 m，最接近S1，岩层破裂角为75.7°，取煤柱宽度为55+(40-39.25)≈56 m。结果汇总如表3所示。

图9不同断面处斜井管片结构随回采工作面位置不同而变化的平均位移(竖向位移以向上为正，水平位移以远离回采工作面方向为正)

Fig. 9 Average displacement vs. distance between coal mining working face and inclined shaft

(a) 竖向收敛值

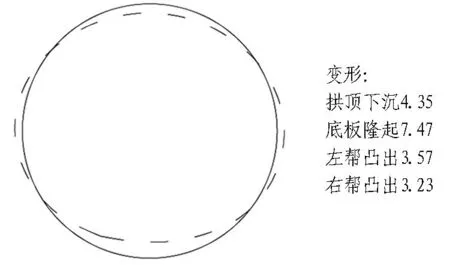
(a) 初始变形

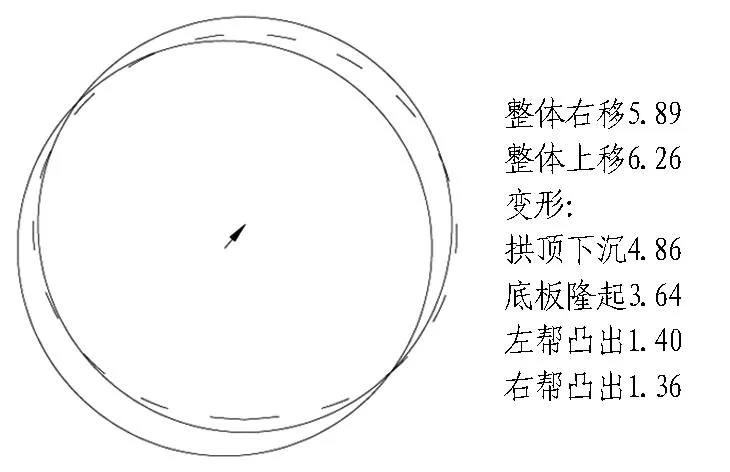
(b) S=290 m

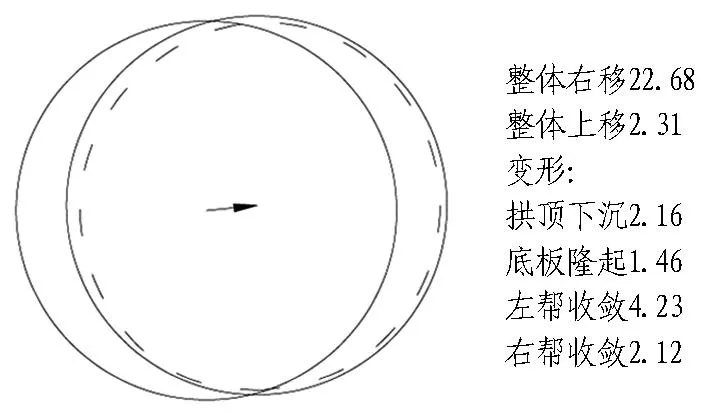
(c) S=130 m

(d) S=70 m

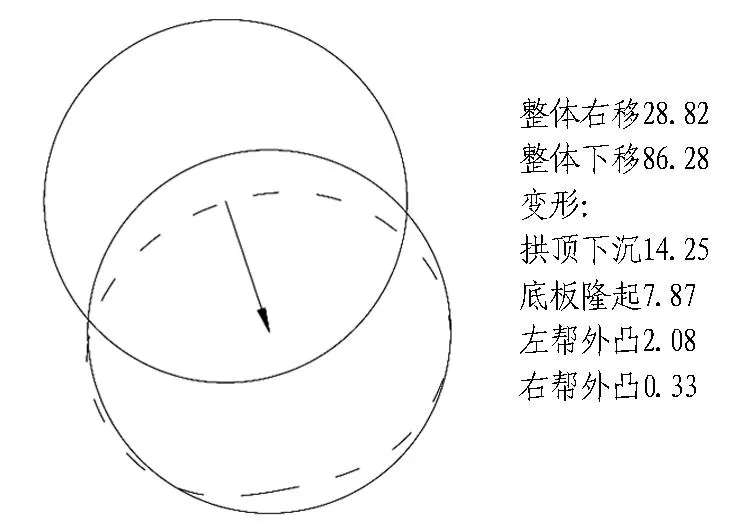
(e) S=25 m

图中箭头表征斜井的位移方向与大小。

图11斜井结构在断面2处的变位特点(单位：mm)

Fig. 11Displacement characteristics of inclined shaft structure at cross-section 2 (mm)

(a) 断面3

(b) 断面4

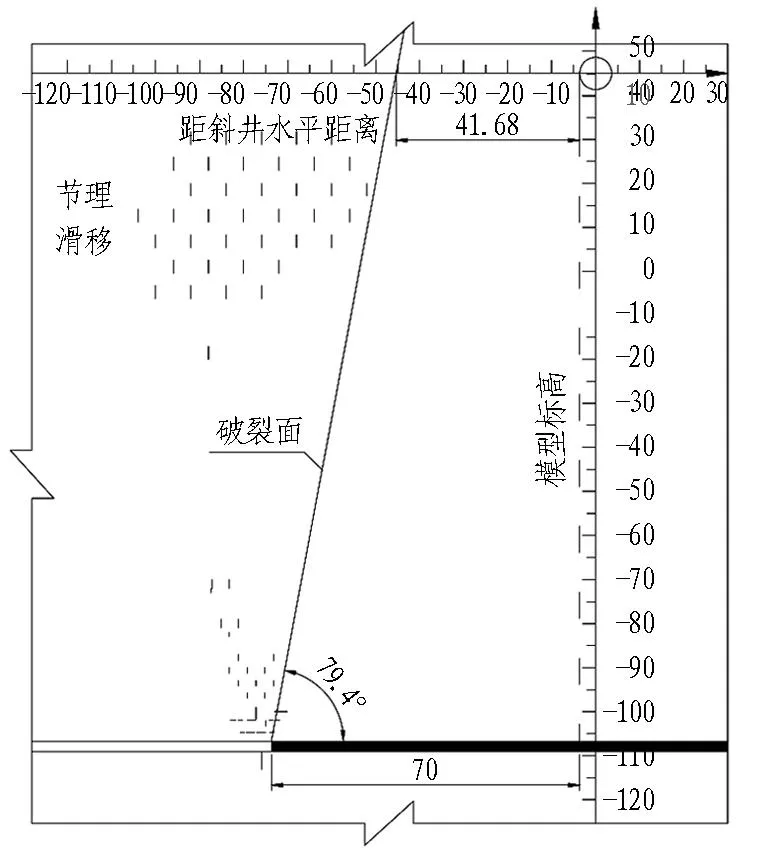
(c) 断面5

模型顶部标高为100 m。

图12基于二维离散元计算的岩层破裂面(单位：m)

Fig. 12Fracture surfaces of rock strata based on 2D discrete element analysis (m)

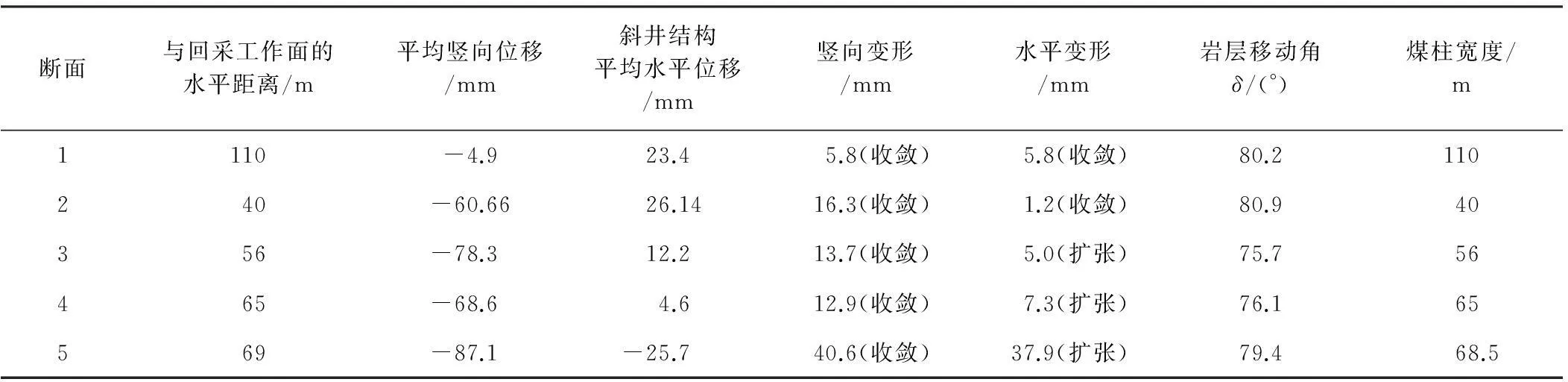
表3　斜井结构变位与煤柱尺寸的计算值

4　经验公式法估算结果与数值模拟结果对比

经验公式法与数值模拟均可以得出岩层移动角和保护煤柱宽度，但前者对分析工作面推进过程中的斜井受力与变位则显得无能为力。2种方法所得煤柱宽度如图13所示。

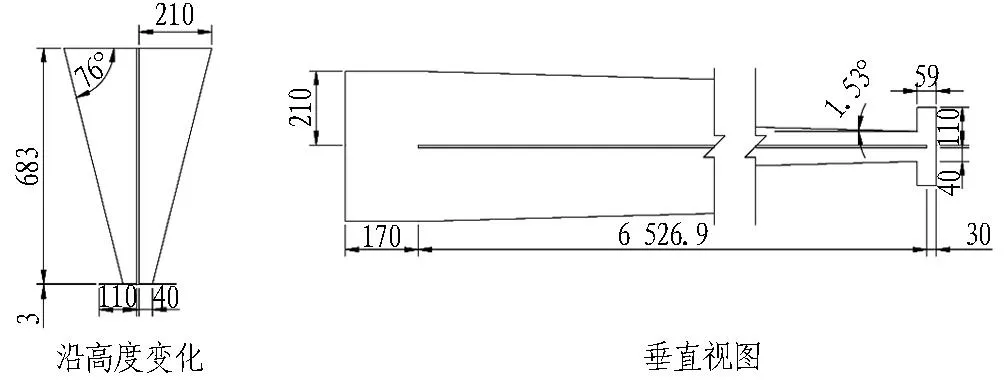
(a) 基于离散元计算

(b) 基于经验公式

Fig. 13Dimensions of protective coal pillar calculated by two methods (m)

经验公式法保护煤柱尺寸：斜井落底处宽41 m，以岩层移动角δ=71°计算保护煤柱宽度，斜井顶部处宽度为276 m。

数值模拟法保护煤柱尺寸：斜井落底处59 m长度范围内宽110 m，然后以宽40 m为基础，按岩层移动角δ=76°计算保护煤柱宽度，斜井顶部处宽度为210 m。

数值模拟与经验公式法结果虽然有相似之处，但是存在以下区别: 1)在计算过程中,数值模拟法更能综合考虑地层与斜井的关系，在斜井落底处的煤柱布设更加合理；2)根据离散元计算得到的煤柱尺寸小于根据经验公式得到的煤柱尺寸，在满足斜井安全和稳定的前提下，可增加矿区的煤炭开采量。

5　结论与建议

保护煤柱的尺寸关乎煤矿的安全稳定与经济效益，必须予以足够的重视。经验公式法只笼统地涉及煤层的几何参数和力学性质，而数值模拟则可以同时考虑煤层、岩层、斜井结构的几何特征和力学特征。保护煤柱的尺寸必须保证煤层开采不会对斜井结构的承载安全性和变位稳定性造成不可接受的影响。本文以东胜煤田新街矿区的开采设计为背景，分别采用经验公式法和二维离散元数值模拟来估算煤柱的合理尺寸，主要结论如下：1)根据二维离散元数值模拟得到的煤柱尺寸小于根据经验公式得到的煤柱尺寸；2)煤层回采工作面与斜井水平距离或竖向距离越小，斜井结构受力状态越不利，反之则越有利；3)随着回采工作面与斜井的水平距离的减小，斜井结构首先轻微上浮，然后显著下沉；4)当斜井与开采煤层的竖向距离较小时，斜井结构因受到破裂岩层的下沉挤压作用而向远离开采工作面的方向变位；5)当斜井与开采煤层的竖向距离足够大时，斜井向开采工作面的方向变位；6)由于斜井穿越岩层与煤层的物理力学性质的差异，在不同岩层或煤层之间的交界面附近，例如斜井结构的落底处，斜井结构可能因应力集中而承载力不足，需要采取一定的改善与控制措施；7)通过经验公式法与数值模拟法的结果对比可知，传统的经验公式法得出的保护煤柱宽度值能够保证煤矿开采的安全，但可能存在一定的资源浪费。

[1]钱鸣高,石平五,许家林. 矿山压力与岩层控制[M].徐州: 中国矿业大学出版社, 2003: 194-197.(QIAN Minggao, SHI Pingwu, XU Jialin. Mining pressure and strata control[M]. Xuzhou: China University of Mining and Technology Press, 2003: 194-197.(in Chinese))

[2]何国清,杨伦,凌赓媂,等. 矿山开采沉陷学[M].徐州: 中国矿业大学出版社, 1994: 243-247.(HE Guoqing, YANG Lun, LING Gengti, et al. Mine exploitation subsidence science[M]. Xuzhou: China University of Mining and Technology Press, 1994: 243-247.(in Chinese))

[3]谢广祥,杨科,常聚才. 煤柱宽度对综放面围岩应力分布规律影响[J].北京科技大学学报, 2006,28(11): 1005-1008.(XIE Guangxiang,YANG Ke,CHANG Jucai. Effect of coal pillar width on the stress distribution law of surrounding rocks in fully mechanized top-coal caving mining face[J].Journal of University of Science and Technology Beijing, 2006,28(11): 1005-1008.(in Chinese))

[4]李学华,杨宏敏,张东升. 下伏煤层开采引起的大巷变形规律模拟研究[J].煤炭学报, 2006,31(1): 1-5.(LI Xuehua, YANG Hongmin, ZHANG Dongsheng. Smiulation analysis of surrounding rock deformation law of main entry with the below seams mined[J]. Journal of China Coal Society, 2006,31(1): 1-5.(in Chinese))

[5]魏峰远,陈俊杰,邹友峰. 留设保护煤柱尺寸的影响因素及变化规律探讨[J].中国矿业,2006,15(12): 61-63.(WEI Fengyuan, CHEN Junjie, ZOU Youfeng. Probing into influence factors and changing laws of coal pillar for protection buildings[J].China Mining Magazine, 2006,15(12): 61-63.(in Chinese))

[6]支光辉,郑彬. 我国保护煤柱留设的方法及发展趋势[J].煤炭工程,2009(6): 9-11.(ZHI Guanghui, ZHENG Bin. Protective coal pillar set method and development tendency in China[J].Coal Engineering, 2009(6): 9-11.(in Chinese))

[7]彭文庆,王卫军. 浅埋厚煤层分层开采保护煤柱合理宽度研究[J].煤炭科学技术,2008,36(11): 14-16,20.(PENG Wenqing, WANG Weijun. Research on rational width of protective coal pillar for slicing mining in thick seam with shallow depth[J]. Coal Science and Technology,2008,36(11): 14-16,20.(in Chinese))

[8]国家煤炭工业局.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程[S].北京: 煤炭工业出版社, 2000. (Coal China. Regulations for establishment and exploitation of coal pillars below buildings, water bodies, railways, main shaft and lane[S].Beijing: China Coal Industry Publishing House,2000.(in Chinese))

[9]Kulhawy F H. Stress deformation properties of rock and rock discontinuities[J]. Engineering Geology, 1975, 9(4): 327-350.

[10]Rosso R S. A comparison of joint stiffness measurements in direct shear, triaxial compression, and in-situ[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1976,13(6): 167-172.

[11]Bandis S C,Lumsden A C,Barton N R. Fundamentals of rock joint deformation[J].International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1983,20(6): 249-268.

[12]Itasca Consulting Group Inc. UDEC universal distinct element code user’s guide 4.0[M]. Minneapolis：Itasca Consulting Group Inc.,2005.

[13]朱维申, 王平. 节理岩体的等效连续模型与工程应用[J].岩土工程学报,1992,14(2): 1-11.(ZHU Weishen, WANG Ping. An equivalent continuum model for joints rocks and its application[J]. Chinese Journal of Geotechnical Engineering,1992,14(2): 1-11.(in Chinese))

[14]孟国涛,方丹,李良权,等. 含优势断续节理组的工程岩体等效遍布节理模型强度参数研究[J].岩石力学与工程学报, 2013,32(10): 2115-2121.(MENG Guotao, FANG Dan, LI Liangquan, et al.Study of equivalent strength parameters of ubiquitous joint model for engineering rock mass with preferred intermittent joints[J]. Chinese Journal of Rock Mechanics and Engineering, 2013,32(10): 2115-2121.(in Chinese))

[15]混凝土结构设计规范：GB 50010—2010[S]. 北京: 中国建筑工业出版社,2010.(Code for design of concrete structures: GB 50010—2010[S].Beijing: China Architecture & Building Press,2010.(in Chinese))

Discrete Element Analysis of Design of Protective Coal Pillar of Inclined Shaft of Xinjie Mining Area of Dongsheng Coalfield

YANG Xu1, 2, XIANG Yanyong1

(1. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China;2.ChinaRailwayFifthSurveyandDesignInstituteGroupCo.,Ltd.,Beijing102600,China)

In order to minimize the influence of coal mining on inclined shaft structures, the rational dimensions of protective coal pillar have to be calculated. The coal pillar dimensions are calculated by empirical formula method, 2D discrete element model is established, the distributions of internal force and displacement of segment of inclined shaft are analyzed, and rational dimensions of protective coal pillar are given by considering 5 different cross-sections of ground-inclined shafts. Some conclusions are drawn as follows: 1) The coal pillar dimensions calculated by discrete element model are smaller than that calculated by empirical formulas. 2) The inclined shaft structure uplifts a little and then sinks obviously with the vertical distance between coal mining working face and inclined shafts decrease. 3) The inclined shaft displaces away from coal mining working face as a result of the sagging pressure from the overlying broken rock layers when the vertical distance between coal mining working face and inclined shafts is comparative small. 4) The inclined shaft structure displaces towards coal mining working face when the vertical distance between the coal mining working face and inclined shafts is large enough. 5) The bearing capacity of inclined shaft structure might become insufficient due to stress concentration at the interfaces of rock and coal layers with distinctively different physico-mechanical properties; thus the improvement and control methods are necessary.

coal seam; inclined shaft; segment; coal pillar dimensions; empirical formula method; discrete element simulation

2015-12-09;

2016-03-28

国家科技支撑计划课题支持(2013BAB10B06)

杨旭(1990—)，男，重庆潼南人，2015年毕业于北京交通大学，桥梁与隧道工程专业，硕士，助理工程师，现从事隧道与地下工程勘察设计工作。 E-mail: 977649093@qq.com。

10.3973/j.issn.1672-741X.2016.08.006

U 45

A

1672-741X(2016)08-0924-09