关于圆与椭圆的几个结论
2016-08-31 03:35何明生
高中数学教与学 2016年15期
何明生
(江苏省泰兴市第四高级中学,225411)
关于圆与椭圆的几个结论
何明生
(江苏省泰兴市第四高级中学,225411)
圆与椭圆同属于圆锥曲线,圆可以看成椭圆的一种极限情况.它们之间有许多相似的性质,有些已经被大家熟悉,有些还鲜为人知,现介绍如下,供大家参考.
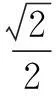
(1)kOA·kOB=-1(直线OA,OB的斜率存在);
(2)OA2+OB2=2r2;
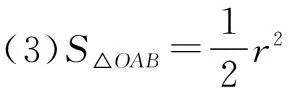
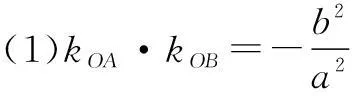
(2)OA2+OB2=a2+b2;

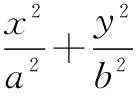
化简得
(1+k2)x2-(2x0+2ky0)x+x20+y20
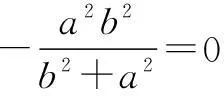
∵直线与椭圆相切,∴Δ=0,即
(2x0+2ky0)2-4(1+k2)(x20
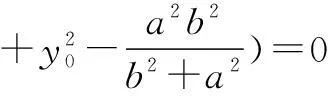
化简得
=0,

b2x20+a2y20=a2b2,
代入(*)得
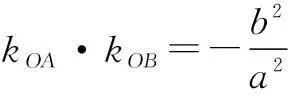
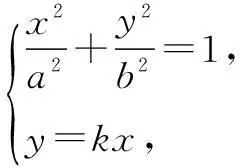


∴OA2+OB2
=a2+b2.
令y=0,解得
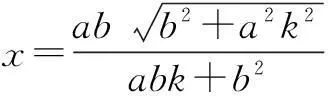
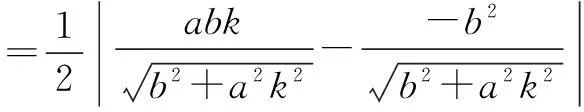
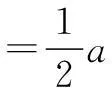
结论2在圆x2+y2=r2上,A,B为圆的直径的两个端点,C为圆上任意一点(除A,B外),则kAC·kBC=-1(直线AC,BC的斜率存在);
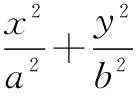
结论3在圆x2+y2=r2上,AB为圆上的一条弦,C为弦AB的中点,则kAB·kOC=-1(直线AB,OC的斜率存在);
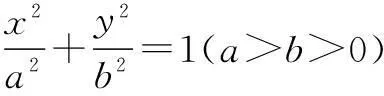
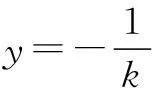
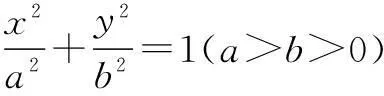
消去y得关于x的一元二次方程:
(b2+a2k2)x2+2kma2x+a2(m2-b2)
=0.

猜你喜欢
小学生学习指导(高年级)(2022年10期)2022-11-04
江苏安全生产(2022年10期)2022-11-02
小学生优秀作文(高年级)(2022年6期)2022-06-27
辽宁教育(2022年6期)2022-05-05
新作文·高中版(2021年4期)2021-07-14
江苏安全生产(2020年2期)2020-04-21
江苏安全生产(2020年1期)2020-03-16
中学生数理化(高中版.高考理化)(2019年3期)2019-04-25
中学生数理化·高一版(2019年3期)2019-04-15
中学生数理化·七年级数学人教版(2017年3期)2018-01-20

