改进的曲率驱动降噪模型

改造者：吴军生



改进的曲率驱动降噪模型

改造者：吴军生

在光照强度较弱的环境中获取的图像强度普遍较低，而且噪声严重，带有大量暗斑。曲率驱动与边缘停止相结合的非线性扩散模型，利用图像等照度线的曲率，可以对弱光下产生的暗斑起到较好的修复作用，利用边缘信息能够在降低噪声的同时保护图像边缘。本文在这一模型的基础上，利用弱光环境下获取的图像强度较低的特点，提出了一种改进模型，利用强度因子增强对暗斑的修复能力，试验结果显示，本文提出的改进有效。

图像与任何其他携带信息形式的数据一样，在每张图片的信息可能受到噪声的影响。图像在获取、传输和存储的过程中都有可能混入噪声，使图像模糊不清，影响图像的分割、重建等后续处理。特别是在低照度环境下，光波粒子较少，不能在图像传感器的所有像素点产生有效的光电效应，进而导致输出的图像与目标图像差别较大，噪点较多，这一点在移动通信设备上尤为明显。由于移动设备体积有限，光圈进光量不足，单像素传感器面积小，导致移动设备对降噪算法依赖极大。

关于图像降噪的算法常见的有：中值滤波法，均值滤波法，双边滤波法，最小均方差滤波等传统的滤波方法，也有基于傅立叶变换的方法和小波变换方法。偏微分方程（PDE） 自上个世纪80年代末开始被用于解决传统的计算机视觉问题，近年来在图像去噪与修复等方向的应用中已经取得了不错的成果。

曲率驱动与边缘停止相结合的非线性扩散模型

偏微分方程是以运动的视角来处理图像问题，起源于物理环境中热传导方程初始值问题：

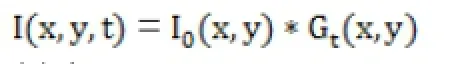
其中，

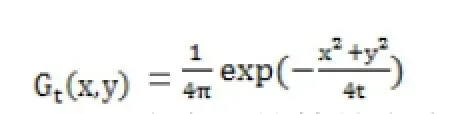
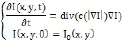
为了克服热方程各项同性模糊图像的问题，以及达到对图像各区域内部平滑，而边缘区域增强的各向异性扩散效果。P-M 模型采用扩散系数函数用以判断算法在t时刻处理的图像区域为平坦区域还是边界区域。当处理区域为平坦区域时，设定扩散系数为1，P-M模型退化为热方程，模型进行平滑处理；当处理区域为边界区域时，设定扩散系数为0。

随着对图像表征认识的深入，人们逐渐认识到一阶微分量（梯度）并不是唯一的图像局部特征，而二阶微分量中含有更丰富的局部信息， Alvarez，Lions和Morel提出了一种沿垂直于图像梯度方向的偏微分扩散方程，模型为：

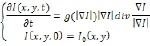
随后又有人对其作适当变换，可以得到如下方向扩散模型：

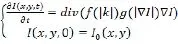
其中表示曲率：

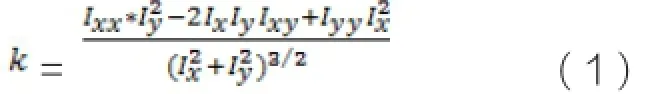
由于图像的任一水平集的曲率可以表达为（1）式，方向扩散模型等价于对图像I的所有水平集曲线C作曲率运动。这里的应使时值为0，值较大时值为1，即该方法平滑较大的等照度线，保护较小的等照度线，同时保护图像的边缘信息，因此对梯度模值足够大的区域应该加以保护。

改进的曲率模型

弱光环境下采集到的图像有一个比较明显的特点是“暗斑”比较大，这主要是由于光照不足，从物体上返回的光波粒子不足以在感光器件上产生足够的电荷，使得获取的图像与实际物体误差较大，不能真实地反映现实世界，故此有必要适当增强图像的强度弥补光粒子不足产生的偏差。

由上一节知，曲率驱动与边缘停止相结合的非线性扩散模型对曲率较大的非边缘区域做平滑处理，对区域边缘或曲率小的区域实施保护不做平滑处理，但是该模型并没有对光照较弱的区域做强化处理，于是加入强度补偿因子。

低照度环境的图像强度通常较低，并且强度越低，所需补偿越大；强度较大时不需要做补偿，于是该因子需满足如下两个条件：

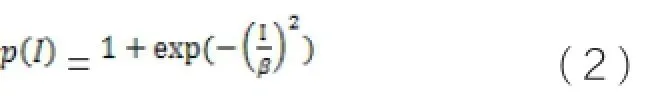
加入强度补偿因子后得到如下模型：

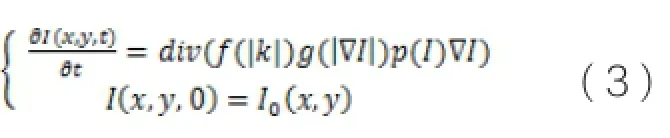
图2为加入强度因子前后处理结果的直方图分析结果，上图是引入强度因子前原模型处理后的分析结果，下图为改进版模型分析结果，上下两图对比可以看出加入强度因子后低强度像素明显减少。

由照度低引起的强度偏差得到了修正，即与原图像的偏差被缩小，因此用该方法降噪比原方法在信噪比的表现上也有一定程度提升。

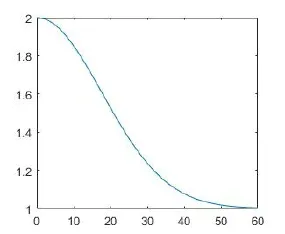
图1　p（I）函数曲线

图2　加入强度因子前后处理结果直方图对比

图3　加噪图σ=50

图4　结果对比

实验结果

为了验证并比较本文提出的方法，首先对图片进行了多种强度噪声的干扰。

由于处理的是弱光条件下的噪声，这里添加的噪声均值和方差均较强，混入不同强度噪声的噪效果如图3所示。

为了验证本文改进模型的效果，采用多种降噪方法进行对比，分别是中值滤波法，双边滤波法，和原曲率模型。

对加入µ=-10，σ=50 噪声的图像进行降噪处理得到如图4所示结果。

从图4中可以看出本文方法在暗处对暗斑较少，而亮处并无明显去斑处理，符合预期。

为分析几种模型对图像强度分布的影响，对以上结果进行直方图分析，如图5所示。

由图5可见，加入噪声后像素值较低的点大幅增多，四种滤波方法均可不同程度的提升像素分布，原模型由于曲率的作用，对强度分布有较明显拉升，低强度像素点大为较少，改进的曲率模型在此基础上又有一定的提高。

下面采用PSNR峰值信噪比对模型降噪性能进行分析。

PSNR计算公式为：为像素的最大值MAX，8位 256色图像MAX=255

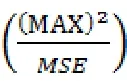
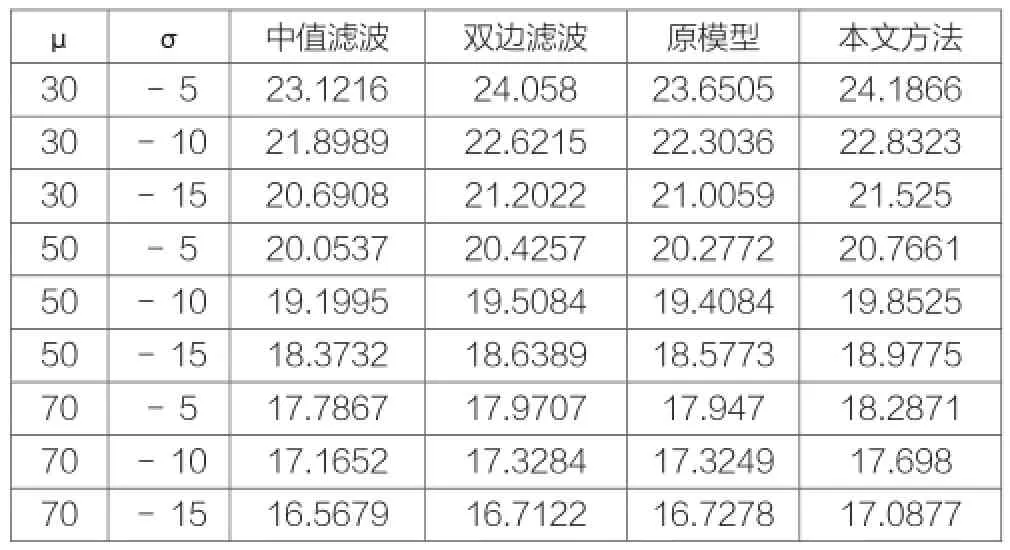
表1　结果对照表

其中MSE为均方误差

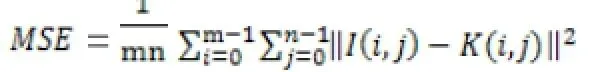
表1是对不同强度噪声下四种处理方法的结果对比，可以看出本文方法处理后PSNR较高。

结语

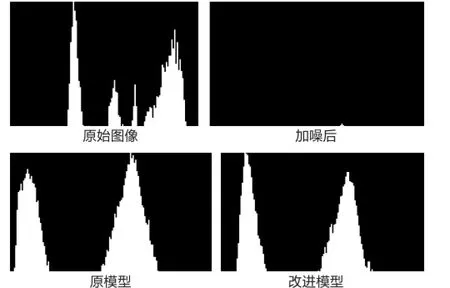
图5　直方图分析结果

本文以曲率驱动与边缘停止相结合的非线性扩散模型为基础，加入强度因子，在利用曲率去除噪声，保护图像边缘信息的同时，提升了弱光环境下图像的修复能力，减弱了因光照不足而产生的偏差。从上一节的实验结果中可以看出，与其他滤波算法相比，引入强度因子的曲率模型可以区分光照强度，并减弱低强度区域的“暗斑”。

吴军生北京邮电大学数学系

吴军生，男，硕士，北京邮电大学数学系，主要研究方向为应用数学。

10.3969/j.issn.1001-8972.2016.01.033