基于LuGre摩擦模型补偿的动态电液测力建模与实验研究*
孙炳玉 吴 询 宋孝臣 焦雷浩 赵延治
(①徐工挖掘机械有限公司,江苏 徐州 221004;②郑州煤矿机械集团股份有限公司,河南 郑州 450000;③北京机床所精密机电有限公司,北京 100102;④燕山大学机械工程学院,河北 秦皇岛 066004)
基于LuGre摩擦模型补偿的动态电液测力建模与实验研究*
孙炳玉①吴询②宋孝臣③焦雷浩④赵延治④
(①徐工挖掘机械有限公司,江苏 徐州 221004;②郑州煤矿机械集团股份有限公司,河南 郑州 450000;③北京机床所精密机电有限公司,北京 100102;④燕山大学机械工程学院,河北 秦皇岛 066004)
为提高电液测力系统在动态下测量其负载的精度,采用LuGre摩擦模型描述动态测力时摩擦力非线性特征,搭建了基于比例阀压力控制的动态电液测力系统,对其在不同油液压力、速度下的摩擦力进行测量,依据实验数据及动、静态参数辨识模型辨识得到动、静态参数,进一步研究油液压力及移动速度对LuGre模型中各个参数的影响,得到关于油液压力及移动速度的LuGre摩擦模型,之后对油液推力实时补偿,得到基于LuGre摩擦模型补偿的动态电液测力精度。实验结果表明,动态电液测力状态下库仑摩擦力、最大静摩擦力及动态参数随油液压力的增大而变大,粘性摩擦系数和Stribeck速度随油液压力的增大而降低;基于LuGre摩擦补偿的动态电液测力系统测量精度可达0.45%。
电液测力;动态;LuGre摩擦模型;测量精度
液压系统具备的功率密度大的特点使其被广泛应用于重载测力领域[1],其在大吨位力的测量场合具有明显优势。近年来,随着对大吨位动态力测量精度要求的不断提高,许多学者开展了对电液测力系统核心执行元件液压缸的摩擦研究,利用摩擦模型描述液压缸摩擦的非线性特性,黎波等[2-3]基于不同的摩擦模型研究了工程机械液压缸摩擦的非线性特征;S. Tafazoli[4]及刘强[5]等将摩擦模型描述的液压缸摩擦系统应用于伺服控制中;LuGre摩擦模型可以很好地描述零速附近摩擦的非线性特性[6],被广泛用于摩擦非线性特性研究中[7-8],如刘伯希等[9-10]基于LuGre模型研究了有杆抽油系统动态摩擦特性;王勇勤等[11]用LuGre模型修正了液压缸的摩擦特性。
电液测力系统是通过测量油液压力,结合液压缸承载面积求取负载,如俆辅仁[12]考虑计算了密封圈与缸内壁间的摩擦力,液压千斤顶利用线性回归法计算负载[13]。但是,在动态测力状态,油液压力、活塞杆移动速度、油液粘度及润滑等边界条件的变化均会导致摩擦力的变化,以往上述因素对摩擦非线性变化的影响常被忽略,从而限制了动态电液测力系统测量精度进一步的提高。
为了提高电液测力系统在动态测力状态下基于油液压力测量负载的精度,需要准确得到液压缸在不同状态时的摩擦力。本文搭建了动态电液测力系统,得到不同油液压力时,摩擦力与活塞杆伸出速度的关系;借助LuGre模型描述液压缸在动态时的非线性摩擦,考虑电液测力系统常被忽略的油液压力及活塞杆移动速度变化对摩擦模型参数的影响,依据实验数据研究油液压力及移动速度对LuGre摩擦模型中各个参数的影响,得到不同状态下的摩擦力,将之对油液推力补偿后,得到负载的计算值,进而得到基于LuGre摩擦模型补偿的测量精度,并将结果与线性拟合法及接触摩擦补偿法进行了比较。
1 动态电液测力模型建立
动态电液测力是指活塞杆相对缸体具有明显伸出速度时,基于油液压力及活塞杆移动速度求取负载的测力状态。

图1表示简化的电液测力系统核心执行元件活塞式单作用液压缸在动态测力过程中的受力示意图。考虑实际电液测力系统中存在的摩擦力,将其对油液推力补偿后,得到负载计算值,模型如下(忽略活塞杆重力):
F=P1S+f(v)
(1)
式中:F表示液压缸负载的计算值,P1表示油液压力,S表示活塞面积,f(v)表示总摩擦力,v表示活塞杆移动速度。
电液测力系统的测量精度η可表示为:
(2)
式中:Fz表示负载实际值。
2 LuGre模型参数辨识及数值算例
2.1LuGre摩擦模型
(3)
式中:F表示摩擦力;z为鬓毛的平均变形量;σ0为鬓毛的刚度;σ1为微观阻尼系数;fv为粘性摩擦系数;g(v)描述了Stribeck效应;Fs为静摩擦力;Fc为库伦摩擦力;vs是Stribeck速度;v为广义速度。其中Fc、Fs、fv、vs称为静态参数,σ0、σ1称为动态参数。
式(3)所示LuGre摩擦数学模型,包含了Stribeck现象、Dahl摩擦、摩擦滞后现象及临界摩擦等,可以很好地表征相对速度在零附近时的摩擦特性[6],被广泛应用于测量控制补偿领域。
2.2LuGre摩擦模型参数辨识
基于二步法辨识LuGre摩擦模型中的参数,为提高算法初始值选取的合理性以提高参数辨识精度,在对静态参数辨识过程中提出在粗略辨识的基础上进行精确辨识。
2.2.1静态参数辨识。
粗略辨识是依据Stribeck摩擦模型在低速及高速下分开辨识,精确辨识是将粗略辨识得到的参数值作为精确辨识的初始值,用变尺度法或非线性最小二乘法辨识静态参数。
(1)粗略辨识[14]
在高速阶段,依据实验数据中的速度-摩擦力值(vi,fi),用最小二乘法求得参数Fc及fv:
(4)
在低速阶段,求得:
(5)
式中:N表示实验数据点采集数量;vi、fi分别表示第i个数据点对应的速度及摩擦力(i=1,…,N),yi=ln(fi-fc)。
(2)精确辨识
将粗略辨识结果作为精确辨识算法的初始值,用变尺度法或最小二乘法对静态参数进行辨识。当接触面间存在相对速度时,鬓毛弯曲速度dz/dt可视作为零,LuGre摩擦模型可变为:
F=Fc+(Fs-Fc)e-(v/vs)2+fvv
(6)
式(6)即Stribeck摩擦模型。以粗略辨识结果为初始值,用变尺度法与非线性最小二乘法对式中参数分别辨识,得到静态参数的精确辨识值。
2.2.2动态参数辨识

在LuGre摩擦模型中,参数σ0、σ1是表示了运动副两接触表面在粘性状态下摩擦力与预滑动位移之间的关系,σ0表示鬓毛刚度,σ1表示微观阻尼系数。可将预滑动位移区的缸-塞系统等效成如图2所示的滑块模型,其中m表示活塞质量。
(7)

(8)
当测出缸-塞系统的固有频率ωn与相对阻尼比ξ后[14],便可得:
(9)
由于在预滑动位移区内ωn与ξ不易求得,故基于胡克定律求:
σ0=fs/max(z)
(10)
其中,相对阻尼比ξ一般取值0.2<ξ<0.7[9],只需测得鬓毛刚度σ0,即可据式(10)得到动态参数辨识值。
2.3LuGre摩擦模型静态参数辨识数值算例
首先经粗略辨识得到静态参数,然后将其作为精确辨识的初始条件值,分别用非线性最小二乘法和变尺度法对参数进行辨识,得到静态参数的粗略及精确辨识精度如表1、2所示。
表1粗略辨识精度

FcFsvsfv理论值1025000.15600辨识值相对速度较大时10.021599.84相对速度较小时2501.40.157辨识精度/%0.210.0564.670.027
表2精确辨识精度

FcFsvsfv初始值取表1粗略辨识值变尺度法辨识值9.9742500.80.145597.7辨识精度/(%)0.260.0323.330.38非线性最小二乘法辨识值9.9922499.30.151599.94辨识精度/(%)0.080.0280.670.01
对比结果可知,精确辨识后的精度可达0.7%以下;非线性最小二乘法辨识的综合精度比变尺度法辨识精度提高13%以上。
3 动态电液测力实验系统
3.1动态电液测力实验系统搭建
动态测力就是液压缸在不同油液压力及活塞杆伸出速度时,观测液压缸内油液压力、负载变化及它们之间的关系,然后根据油液压力及伸出速度计算其负载的过程。

系统示意图及实物图如图3、4所示,主要包括液压站、比例阀、电液测力模块及位移传感器、压力传感器等信号采集处理系统及控制系统,另外使用液压力机作为反力架,以液压缸为核心的电液测力模块,主要包括液压缸、位移传感器、油液压力传感器及力源传感器。

在压力机及比例阀作用下,使油液压力保持稳定,液压缸活塞杆以不同的速度伸出,然后调定其它油液压力重复上述过程,最后得到油液压力、负载及活塞杆移动速度关系。

按照图5所示数据处理流程图,结合实验数据,在动态测力状态下,经过多次实验以保证系统具有重复性基础上,辨识求得LuGre摩擦模型,最后将其应用到数据实时处理中,求得基于LuGre摩擦补偿的测量精度等。
3.2基于实验数据的LuGre模型参数确定
(1)静态参数确定
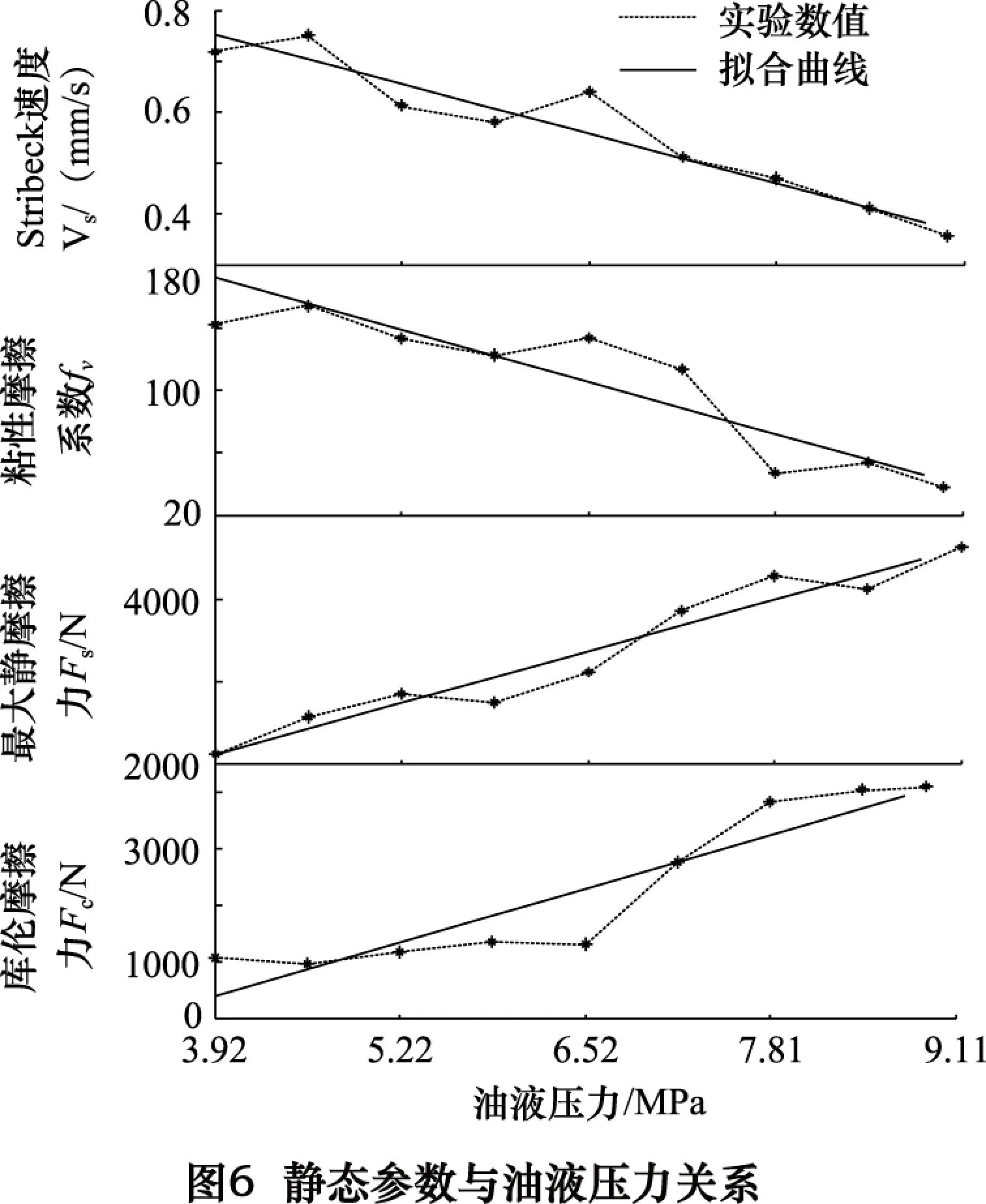
根据系统在不同油液压力时的LuGre摩擦模型,得到同一静态参数关于油液压力的变化关系,如图6所示。
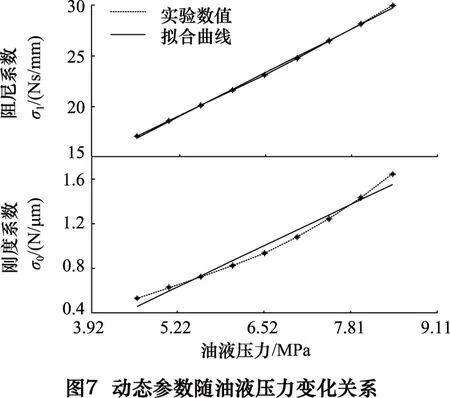
(2)动态参数确定
根据实验数据,可得到液压缸在某个油液压力下的最大预滑动位移区max(z),依据式得到此负载对应的鬓毛刚度σ0及微观阻尼系数σ1。设定在不同油液压力时,假定阻尼比ξ=0.5,得到对应的鬓毛刚度σ0及微观阻尼系数σ1,如图7所示。
依据实验结果可知,动态电液测力系统的LuGre摩擦模型中,静态及动态参数关于油液压力的关系可表示为:
f(P)=kSP+b
(11)
其中:f(P)=[Fc,Fs,vs,fv,σ0,σ1]T表示LuGre摩擦模型中静、动态参数,是关于油液压力P的函数;P表示油液压力MPa:S表示活塞面积;k表示油液压力对静、动态参的数影响系数,k=[kc,ks,kvs,kv,kσ0,kσ1]=[731.2,482.9,-0.075,-25.9,211.6,2.37];b可表示为:b=[bc,bs,bvs,bv,bσ0,bσ1]T=[-2476.6,219.0,1.048,274.2,-373.5,6.61]T。
3.3基于LuGre摩擦补偿的测量精度
由油液压力及式可得到动静态参数,从位移传感器可知活塞杆移动速度,代入式(3)得到LuGre摩擦力,对油液推力补偿后,得到系统负载的计算值。油液压力P为3.92、6.52及9.11 MPa时辨识得到的Stribeck摩擦力,如图8所示。
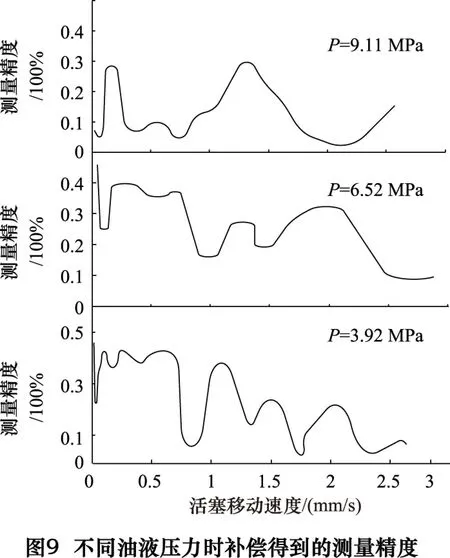
依据辨识得到的LuGre摩擦力,对油液推力补偿,得到负载计算值,与力源传感器数值相比得到基于LuGre摩擦模型补偿的测量精度,如图9所示。
由图9结果可知,对于不同油液压力及活塞杆移动速度下,对油液推力补偿后的测量精度数值较为稳定,在速度1 mm/s以上时,测量精度达0.4%。

3.4测量精度对比分析
(1)线性拟合法测量精度
忽略活塞杆伸出速度对摩擦力影响,在不同油液压力时,用线性拟合法得到的测量精度如表3所示,可知线性拟合后测量精度达到0.9%以内。
(2)接触摩擦补偿法测量精度
简化液压缸密封圈为O形圈,按照文献[12]提供的液压缸动态摩擦计算方法,忽略活塞杆伸出速度对摩擦力影响,用接触摩擦补偿法求得的测量精度如表3所示,可知基于接触摩擦补偿的测量精度达到0.7%以内。
将基于LuGre摩擦补偿法与接触摩擦补偿法和线性拟合法的实验数据处理结果值整理,得到对应测量精度,如表3所示(其中直接测量精度表示油液压力与活塞面积乘积得到的计算负载精度)。
表3不同方法得到的动态电液测量精度(%)

油液压力/MPa3.926.529.11直接测量精度1.921.891.86线性拟合测量精度0.880.810.89接触摩擦补偿精度0.620.690.68LuGre摩擦补偿精度0.450.420.28
通过表3可知,基于LuGre摩擦模型补偿求得的动态电液测力系统的测量精度可达0.45%,比接触摩擦补偿法得到的测量精度0.69%提高35%,同时比线性拟合法得到的测量精度0.89%提高50%。
4 结语
(1)搭建了动态电液测力实验系统,将实验数据作为边界条件对LuGre摩擦模型静态参数在粗略辨识基础上进行精确辨识,数值算例证明得到参数辨识值接近实际值。
(2)LuGre动静态参数辨识结果表明库仑摩擦力、最大静摩擦力及动态参数随油液压力的增大而变大、粘性摩擦系数和Stribeck速度随油液压力的增大而降低。最小摩擦力对应活塞杆移动速度随油液压力的增大而减小。
(3)基于LuGre摩擦补偿法得到的电液测力系统在动态下的测量精度可达0.45%,相比其他补偿方法提高了动态电液测力系统测量精度。
[1]李壮云. 液压元件与系统[M]. 北京: 机械工业出版社, 2011.
[2]黎波, 严骏, 郭刚,等. 挖掘臂的液压缸摩擦模型辨识与分析[J]. 机械科学与技术, 2013, 32(6): 814-818.
[3]龚文, 王庆丰. 液压挖掘机上车结构参数与液压缸摩擦力参数辨识[J]. 中国机械工程, 2010, 21(9): 1098-1105.
[4]Tafazoli S,Silva C W,Lawrence P D. Tracking control of an electrohydraulic manipulator in the presence of friction[J]. IEEE Transactions on Control Systems Technology. 1998.
[5]刘强, 扈宏杰, 刘金琨,等. 基于遗传算法的伺服系统摩擦参数辨识研究[J]. 系统工程与电子技术, 2003, 25(1): 77-79.
[6]Canudas-de-wit C, Olsson H, Astrom K J, et al. A new model for control of system with friction[J]. IEEE Transactions on Automatic Control, 1995, 4(3): 419-425.
[7]Guerra R, Acho L, Aguilar L. Adaptive friction compensation for mechanisms: a new perspective[J]. International Journal of Robotics & Automation, 2007, 22(2): 155-159.
[8]Zeng H, Sepehri N. Tracking control of hydraulic actuators using a LuGre friction model compensation[J]. Journal of Dynamic Systems Measurement and Control, Transactions of the ASME, 2008, 130(1): 116-122.
[9]刘伯希, 刘宏昭. 基于LuGre摩擦模型的定向井有杆抽油系统动态参数预测[J]. 石油学报, 2008, 29(6): 938-941.
[10]刘伯希, 刘宏昭. 基于LuGre摩擦模型的有杆抽油系统动态特性分析[J]. 中国机械工程, 2009, 20(18): 2236-2239.
[11]王勇勤, 张洋, 罗远新,等. 基于 LuGre 模型的液压缸摩擦力修正模型[J]. 润滑与密封, 2014, 39(10): 6-9.
[12]俆辅仁. 油缸内O形圈所产生的总摩擦阻力的分析和研究[J], 机床与液压, 1990(4): 21-27.
[13]国家质检总局.JJG 621-2012 液压千斤顶[S]. 北京:中国质检出版社、中国标准出版社,2012.
[14]吴子英. 构件阻尼和运动副摩擦参数辨识的理论与实验研究[D]. 西安: 西安理工大学, 2007.
(编辑汪艺)(收修改稿日期:2015-01-14)
如果您想发表对本文的看法,请将文章编号填入读者意见调查表中的相应位置。
Modeling and experimental research on dynamic electro-hydraulic force measurement based on LuGre friction compensation
SUN Bingyu①, WU Xun②, SONG Xiaochen③, JIAO Leihao④,ZHAO Yanzhi④
(①XCMG Xuzhou Mining Machinery Co., Ltd., Xuzhou 221004, CHN;②Zhengzhou Coal Mining Machinery Group Company, Zhengzhou 450000, CHN;③BMTI Precision Mechatranics Co., Ltd., Beijing 100102,CHN;④College of Mechanical Engineering, Yanshan University,Qinhuangdao 066004, CHN)
To improve the accuracy of electro-hydraulic force measurement in dynamic environment, the nonlinear friction in measurement system is described based on LuGre friction model, the electro-hydraulic force measuring system is built based on pressure control of proportioner, the friction in different pressure and speed is measured, further research about the affection of pressure and speed on every parameters in LuGre model is analyzed according to the experiment data and dynamic parameter identified through the identification model, and the LuGre friction model about pressure and speed is got, then the accuracy of electro-hydraulic force measuring system based on LuGre friction model compensation is got. Experimental results show that the Coulomb friction, dynamic parameters and maximum static friction increase as the oil pressure increases, and the Stribeck speed and viscous friction coefficient decrease with the increase of oil pressure; the accuracy reach to 0.45% in the electro-hydraulic force measurement based on LuGre friction compensation.
electro-hydraulic force measurement; dynamic; LuGre friction model; measurement accuracy
TH823;U262.32+1
B
孙炳玉,男,1980年生,博士,工程师,研究方向为工程机械液压控制技术。
160416
*国家自然科学基金( 51105322) ; 河北省自然科学基金( E2014203176) ; 河北省高等学校科学技术研究青年基金( QA2015040)

