冷镦机床身应变能与体积双目标拓扑优化*

何　彬

(湖北理工学院机电工程学院，湖北 黄石 435003)



冷镦机床身应变能与体积双目标拓扑优化*

何彬

(湖北理工学院机电工程学院，湖北 黄石 435003)

机床床身多目标拓扑优化主要存在优化目标冲突、收敛慢、计算量大等问题。以冷镦机床身结构整体刚性与减重效果为优化指标，提出一种改进的应变能与体积双目标多约束优化列式，并结合权重调整和单目标函数自约束两种方法，运用Abaqus6.12，对某型号冷镦机床身进行数值仿真和分析，结果表明，权重调整可以弱化优化过程中体积对应变能的影响，应变能自约束能够加快收敛过程，两者对于改善冷镦机床身应变能与体积双目标拓扑优化的求解过程，获得理想的优化结果是可行的。

冷镦机；床身；双目标；拓扑优化；应变能；体积

(School of Mechanical and Electrical Engineering, Hubei Polytechnic University, Huangshi 435003, CHN)

冷墩机是应用冷墩工艺生产各类标准件、紧固件、异形件的工作母机。冷镦机床身是整机中重量最大的一部分，约占整机重量的30%～45%，对冷镦机床身进行轻量化设计是节材和降低成本的必然途径[1]。从现有文献看，对机床床身的轻量化设计多采用拓扑优化方法[2-3]，如分别以应变能、体积或固有频率为目标函数的单目标优化[4-6]，但单目标拓扑优化很难保证较优的床身综合性能；在多目标拓扑优化中，文献[7]以床身的质量作为主要优化目标、一阶固有频率和最大变形作为次要优化目标进行多目标优化设计；文献[8]以外圆磨床床身结构刚度和基频为设计目标；文献[1]运用折衷规划法，以重量和整体刚度为指标，对冷镦机床身展开多目标优化。

机床床身多目标拓扑优化至少有两个方面的问题还值得探讨：第一，如何解决目标函数之间的冲突。一个目标函数减小导致其他目标函数增加称之为目标函数之间的冲突，此情形下很难得到最优值[9]；第二，如何合理规划优化模型，加快收敛，减少计算量。尤其是非线性优化模型，尽管拓展了寻优空间，但收敛慢，计算量大。

针对上述问题，本文以冷镦机床身结构应变能与体积为目标，采用一种改进的多约束优化列式，并通过权重调整和单目标函数自约束两种方法，验证冷镦机床身应变能与体积双目标拓扑优化过程的可行性。

1　双目标拓扑优化列式

对于多目标拓扑优化，更多是采用线性加权法将多目标问题转化为单目标问题来求解，这样可以简化优化计算过程，实现起来比较容易，但同时也缩小了优化空间，尤其对非凸优化问题而言，不能确保得到所有的Pareto最优解[9]。因此，有些研究通过折衷规划法来建立冷镦机床身多目标优化模型，如文献[1]。但对于冷镦机床身这种复杂的三维实体结构，采用非线性优化模型不仅计算量大，而且优化列式中的最小应变能和最小体积皆通过预估来确定，在一定程度上降低了优化求解精度。同时，冷镦机床身结构体积与应变能不是相互独立的目标函数，应变能函数为单元应变能之和，通过拓扑优化过程中单元的删减来减少体积，对应变能大小难免会造成影响。由于总应变能反映了冷镦机床身的整体刚性，因此可以在优化模型中增加最大位移约束，最大位移是衡量冷镦机床身整体刚性的重要指标，设置最大位移约束不仅是冷镦机加工精度的保证，还可以弱化体积改变对应变能造成的影响；同时，为了保证冷镦机床身的强度，需要考虑最大应力约束，这也可以在一定程度上缩小寻优范围，增加收敛性，减少计算量。

按照上述思路，冷镦机床身应变能与体积双目标拓扑优化列式可以表达为：

(1)

其中：X=[x1,x2,…,xn]为双目标拓扑优化设计变量；xi为单元伪密度，在0～1之间取值；n为单元个数；F(X)为目标函数；C(X)为冷镦机床身结构总应变能；C0为床身初始总应变能；W为对应权重；V(X)为床身结构总体积；V0为床身初始结构总体积；σmax(xi)为单元的最大应力值；σ为许用应力值；γmax(xi)为单元最大位移；γ为许用最大位移值；δ为消除奇异的单元密度最小极限值，一般取0.000 1[4]；s.t.3为待定约束。初始总应变能和初始体积总是比优化过程中的对应值大，而且初始总应变能和初始体积在拓扑优化启动阶段由有限元软件自动计算出，容易确定，因此可以通过结构总应变能与初始总应变能的比值以及结构总体积与初始结构总体积的比值实现归一化。

由于拓扑优化过程中，结构总应变能和结构总体积相对初始值的改变程度不一样，因此权重是影响求解过程的重要因素，同时，为了得到更为理想的优化结果，仍然可以考虑增加待定约束。基于上述优化模型，以下运用实例，分别通过权重调整和单目标函数自约束两种方法，来对冷镦机床身应变能与体积双目标拓扑优化过程展开研究。

2　权重调整法

本文中的权重调整法是通过改变优化列式中的权重，并逐一进行仿真和逼近，来获得较为理想的双目标优化结果的一种数值模拟方法。以某型号冷镦机床身为例，初始床身结构参照文献[4]和[10]，初始结构总体积为1.426 4 m3，工作中左边前压板和右边前后轴承孔为主要受力部位，最大公称力为410 kN，床身材料为HT250，根据HT250材料的抗拉强度和安全系数以及该型号冷镦机加工精度要求，可以设置最大许用应力125 MPa和最大许用位移0.07 mm。

首先将权重设置为0.5，在Abaqus6.12建立模型、定义约束和参数并提交任务，在设计循环尚未启动时读取床身初始总应变能为100.087 N·m，再根据权重、初始总应变能和初始体积值设置目标函数，最后运用ATOM模块展开优化进程，经过15次设计循环，目标函数F(X)的值已趋于收敛，如图1所示。而此时应变能为28.575 7 N·m，体积为0.714 27 m3，最大应力为48.62 MPa，最大位移为0.115 mm。其中，最大位移大于0.07 mm，在目标函数已经收敛时，仍然不满足约束要求，说明在给定的约束下权重为0.5时的双目标优化过程无解，为此需要重新调整权重系数。

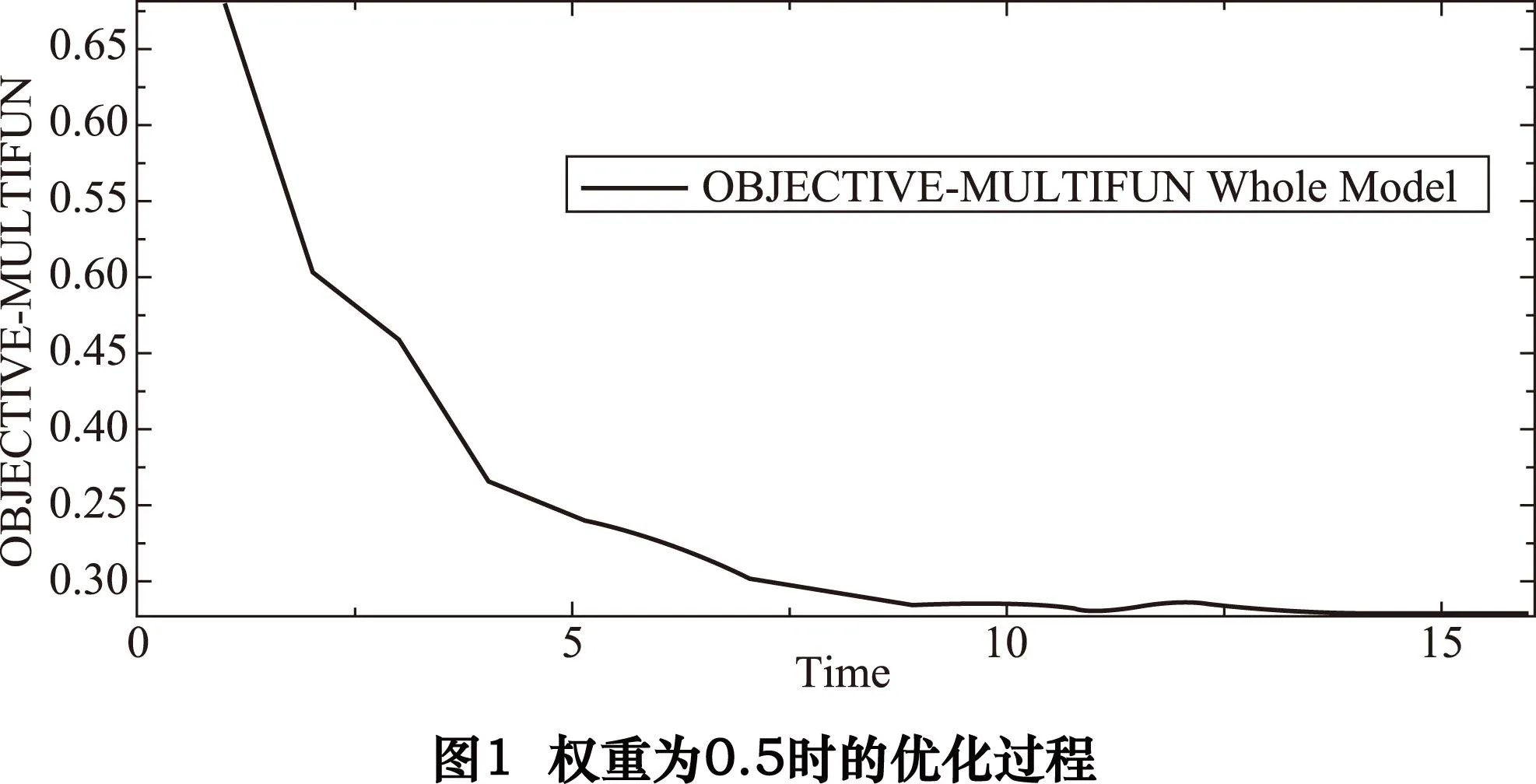
将权重系数依次设置为0.6、0.7和0.8，调整相应的参数设置，并重复上述步骤，分别进行仿真，得到的优化结果如表1所示。

权重从0.5到0.8改变时，可以看出，目标函数、应变能和最大位移递减，体积和最大应力递增，当权重为0.5、0.6和0.7时，最大位移都不满足设定的约束要求，直到权重调整为0.8，所有约束要求才在优化结果中得到满足，其中体积减幅为30.06%，对照文献[4]中以应变能为函数、体分比、最大应力、最大位移为约束的单目标优化结果，在体积减幅达到31%～33%时，应变能的值在23.9～24.2 N·m之间，说明权重为0.8时床身的整体刚性超出了预期值，但减重效果还不理想，为此可以在权重0.7～0.8之间重新寻求合理的权重，通过有限元逐步仿真逼近可以得到相对较优的权重，即当权重为0.76时，目标函数、应变能、体积、最大应力和最大位移分别为0.341 673、23.952 3 N·m、0.949 4 m3、48.83 MPa、0.678 5 mm，相比而言，优化值更为合理，待优化的两个指标床身整体刚性和重量可以达到一个较为理想的效果。

表1调整权重的优化结果

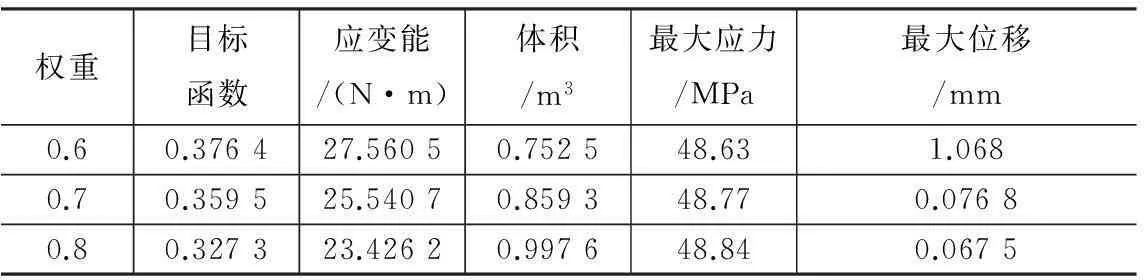
权重目标函数应变能/(N·m)体积/m3最大应力/MPa最大位移/mm0.60.376427.56050.752548.631.0680.70.359525.54070.859348.770.07680.80.327323.42620.997648.840.0675

3　单目标函数自约束法

基于优化列式(1)，采用权重向应变能函数倾斜的调整方法可以减小体积改变对应变能的影响，从而弱化两个目标函数之间的冲突，但是权重调整是一个试凑的过程，耗时较长。单目标函数自约束法就是对某一个单目标函数进行约束，增加到优化列式(1)的待定约束中。优化列式(1)中的应变能函数C(X)和体积函数V(X)是双目标函数F(X)的自变量，对应变能和体积函数进行约束，缩小了自变量的取值区间，可以加快优化过程的收敛，但约束过多也会出现优化无解的情况。因此，分别以体积和应变能为约束，增加到优化列式中，取权重为0.5，验证可行性。体积的约束值可以根据床身的减重目标设定，如文献[4]中小于70%，应变能的约束值可以按照应变能单目标优化结果的中间值进行设定，本例中设为24.14 N·m。在Abaqus6.12中重新增加体积或应变能的约束设置，分别对两种单目标函数自约束情况进行优化仿真。体积自约束优化结果为：目标函数值0.391 7，应变能28.615 6 N·m，体积0.709 34 m3，最大应力48.62 MPa，最大位移0.124 9 mm。同样是在目标函数趋于收敛时无法找到满足最大位移约束的最优解。应变能自约束优化结果为：目标函数值0.443 0(不考虑冻结区域为0.318 1)，应变能24.06 N·m，体积0.920 8 m3，最大应力48.8 MPa，最大位移0.069 1 mm。优化进程、优化后结构以及应力、位移云图分别如图2～5所示。

从上图可知，在经过20次设计循环后，目标函数在满足所有约束的前提下收敛，且床身整体刚性和减重效果较为理想。从优化列式中目标函数的敏度分析可推断，体积对密度设计变量的导数总是为0的，而应变能对密度设计变量的导数不为0，因此应变能的改变是影响目标函数灵敏度的关键因素，对整个优化求解过程和结果起着决定性作用。在本例中，权重为0.5无待定约束时，优化过程是无解的，增加了体积约束仍然无解，但是将体积约束换成应变能约束，则可获得较为理想的优化结果，充分说明了应变能对求解过程的主导作用。

4　结语

冷镦机床身应变能与体积双目标拓扑优化列式是一种改进型的线性优化模型，权重调整和单目标函数自约束是保证优化过程的实现获取理想优化结果的两种方法，权重调整可以弱化优化过程中体积对应变能的影响，应变能自约束能够显著加快收敛过程，提高求解质量。两种方法可根据冷镦机床身的结构和实际工况进行选取，有一定的工程应用和参考价值。

[1]徐高春. 面向环保的高速全自动冷墩机优化研究与系统实现[D]. 上海：上海大学，2011.

[2]Hassani B, Hinton E. Homogenization and structural topology optimization theory, practice and software[M]. London: Springer, 1999.

[3]张永存，崔雷，周玲丰，等. 基于拓扑优化的机床床鞍创新构型设计[J]. 固体力学学报，2011，32(10)：335-342.

[4]He Bin. Multi-constraint topology optimization of forging machine bed for light weight design [J]. International Journal of Advancements in Computing Technology, 2013, 9 (5):94-103.

[5]倪晓宇，易红，汤文成，等. 机床床身结构的有限元分析与优化[J]. 制造技术与机床，2005(2)：47-50.

[6]胡世军，邓洋，韩健，等. 基于Optistruct的数控滚齿机床身拓扑优化设计[J]. 机械制造，2011，49(11)：8-10.

[7]章婷. 基于有限元法的锻压机床床身结构优化设计[J]. 锻压技术，2010，35(6):74-78.

[8]陈叶林，丁晓红，郭春星，等. 机床床身结构优化设计方法[J]. 机械设计，2010，27(8):65-68.

[9]刘林华，辛勇，汪伟. 基于折衷规划的车架结构多目标拓扑优化设计[J]. 机械科学与技术，2011，30(3)：382-385.

[10]何彬. 疲劳寿命约束下冷镦机床身的拓扑优化[J]. 机床与液压，2014，42(22)：50-52.

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Topology optimization with double objective of strain energy and volume for cold heading machine bed

HE Bin

The main problems in multi-objective topology optimization of machine tool bed are the confliction of objective functions, slow convergence and large calculation. Aiming at the optimal indexes of overall rigidness and weight-reducing of cold heading machine bed, multi-constraint optimized model with double objective of strain energy and volume is put forward. Combined with numerical simulation and analysis based on Abaqus6.12, weight adjustment and self constraint of single objective function are used respectively. The results show that weight adjustment can weaken the effect of volume on strain energy and self constraint of strain energy can accelerate the process of convergence. It is feasible for the two methods to improve the solving process and obtain the optimal results of topology optimization for cold heading machine bed.

cold heading machine; bed;double objective;topology optimization; strain energy;volume

TH122

A

何彬，男，1970年生，工学博士，副教授、硕导，主要研究方向为优化设计、机床技术。

(编辑谭弘颖)(2015-10-27)

160319

*湖北省自然科学基金(2012FFC016)