用于电机损耗精细化分析的分段变系数铁耗计算模型
张冬冬 赵海森 王义龙 许国瑞 刘晓芳
(新能源电力系统国家重点实验室(华北电力大学) 北京 102206)
用于电机损耗精细化分析的分段变系数铁耗计算模型
张冬冬赵海森王义龙许国瑞刘晓芳
(新能源电力系统国家重点实验室(华北电力大学)北京102206)
提出一种用于电机损耗精细化分析的分段变系数铁耗计算模型,该模型以经典Bertotti三项常系数铁耗模型为基础,引入涡流损耗附加磁通密度高次项及磁滞损耗附加磁通密度低次项,用于考虑磁路饱和导致涡流损耗增加及谐波磁场引起局部磁滞损耗增加的现象,同时,该模型中主要系数均随磁通密度幅值和频率变化,能很好地反映基波及谐波磁场对铁耗的影响,并对磁滞、涡流及异常损耗进行准确分离,实现铁耗精细化分析。为了验证该文所提模型的有效性及准确性,以Y132S- 4、5.5 kW和YX3-250M- 4、55 kW两台感应电机为例,利用文中模型与经典Bertotti三项常系数模型对两台电机在不同电压下的空载铁耗进行实测和计算对比,结果表明该文所提模型在较宽范围内与实测值吻合程度较高。
电机铁耗磁滞涡流非线性
0 引言
大量电力电子设备和非线性负载的使用,使电网受到的谐波污染越来越严重[1,2],另外,受电机内部磁路饱和、磁化方式等因素的影响,准确计算电机铁耗一直是工程界面临的难点问题。而在高效电机研制过程中,如何准确计算铁耗,并对其进行精细化分析,是获得铁耗主要影响因素的关键环节,在此基础上才能提出有针对性的降耗措施。因此,研究能够用于电机损耗精细化分析的铁耗精确计算模型是高效电机研制中亟待解决的问题。
已有大量国内外文献开展了电机铁耗计算方面的研究[3-9],目前工程界采用较广泛的铁耗计算模型是由G.Bertotti[3]于1988年提出的三项常系数模型,该模型主要包括磁滞、涡流、异常损耗三部分,模型中系数是通过对特定频率及磁通密度下实测硅钢片损耗进行拟合求得,在一定磁通密度及频率范围内、硅钢片特性线性度较好时计算准确度较高,但当偏离上述范围时误差较大,例如该模型在磁通密度大于1.2 T或频率大于400 Hz时,计算值偏低于实测值[5]。为了解决这一问题,研究损耗系数随磁通密度和频率变化的变系数铁耗模型成为一种有效方法,文献[6,7]中针对3种不同硅钢片,提出两项和三项变系数模型,这两种模型的损耗系数都是随频率和磁通密度变化,通过实例计算表明,变系数模型的计算准确度高于常系数模型。但由于变系数模型均通过数值拟合方法将损耗系数表示成频率和磁通密度的多项式,并受多项式拟合病态特性[10]的影响,因此当频率和幅值跨度很大时,也会导致较大误差。
为了解决变系数模型存在的问题,需从铁磁材料非线性特性及铁耗物理本质出发,对组成铁耗的主要损耗项在不同磁通密度及频率条件下的损耗变化规律进行研究,进而提出适用性更广泛、计算准确度更高的计算模型。文献[11-14]指出磁通密度或频率较高时涡流损耗增加较为明显,为了计及涡流损耗的增加,文献[5,15]在Bertotti三项常系数模型中的涡流损耗项中增加磁通密度高次项作为补偿,提出一种含有涡流附加项的铁耗计算模型;在磁滞损耗方面,文献[15-19]研究了谐波磁场引起局部磁滞回环对铁耗的影响规律,指出随着谐波磁场幅值和频率的增加,局部磁滞回环对铁耗影响显著增加。
本文提出一种用于感应电机损耗精细化分析的分段变系数铁耗计算模型,该模型以Bertotti三项常系数模型为基础,引入磁滞损耗附加磁通密度低次项及涡流损耗附加磁通密度高次项,用于考虑磁路饱和导致涡流损耗增加及谐波磁场引起局部磁滞损耗增加的现象。与Bertotti模型相比,该模型引入了4个随磁通密度和频率分段变化的损耗系数。为了验证本文所提模型的有效性,以Y132S- 4、5.5 kW和YX3-250M- 4、55 kW两台感应电机为例,利用本文所提模型与经典Bertotti三项常系数模型对两台电机在不同电压下的空载铁耗进行实测和计算对比,结果表明本文所提模型在较宽范围内与铁耗实测值吻合程度较高。此外,该模型还能很好地反映基波及谐波磁场对铁耗的影响,并对磁滞、涡流及异常损耗进行准确分离,实现铁耗精细化分析,为新一代高效电机研制提供重要理论支撑及技术支持。
1 经典三项常系数模型及存在的问题
1.1经典三项常系数模型介绍
经典三项式常系数模型如式(1)所示。
PBertotti=khBαf+keB2f2+kaB1.5f1.5
(1)
式中,khBαf表示磁滞损耗;keB2f2表示涡流损耗;kaB1.5f1.5表示异常损耗;kh、α、ke、ka为常系数。涡流损耗系数ke可由式(2)求出,系数kh、α、ka是通过对硅钢片实测数据进行拟合得到。
(2)
式中,d为硅钢片厚度,m;ρ为硅钢片密度,kg/m3;ρe为硅钢片电阻率,Ω/m。
1.2三项常系数模型存在的问题
以硅钢片DR510为例,利用三项常系数模型计算得到的损耗与实测损耗对比结果如图1所示。可以看出,在磁通密度B≤1.2 T、频率f≤400 Hz时误差相对较小,超出上述范围后误差越来越大。这主要是由于磁通密度和频率过高导致硅钢片线性度变差,从而导致涡流损耗增加;而随饱和程度增加,磁滞回线会产生局部磁滞回环,从而引起磁滞损耗增加。因此,经典的Bertotti三项常系数模型在此范围内不再适用。
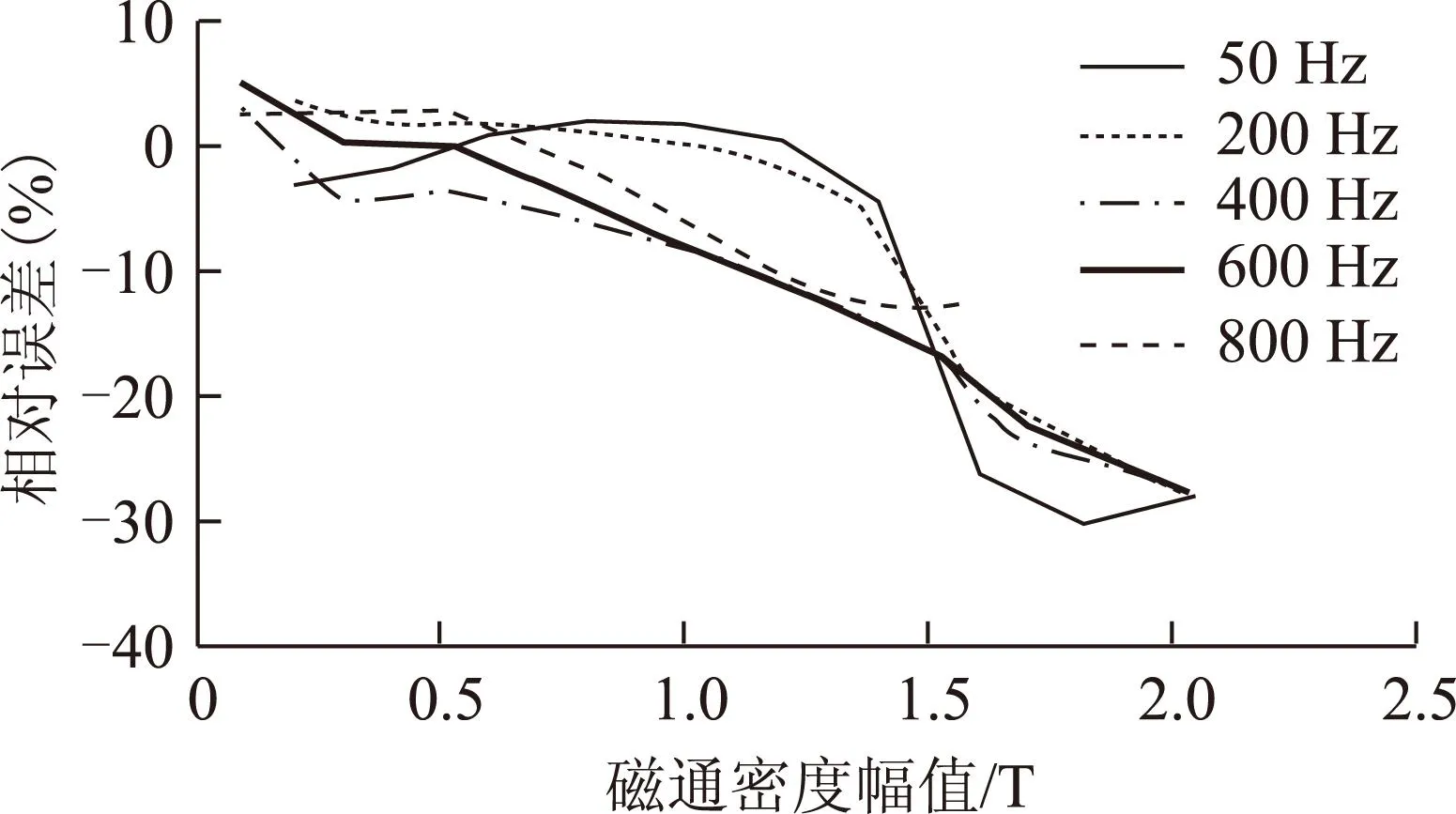
图1 经典Bertotti模型计算的DR510硅钢片相对误差Fig.1 Relative errors of computed losses of the lamination steel DR510 with Bertotti model
1.3三项常系数模型存在的问题
在高频和高磁通密度时,式(1)计算的经典涡流损耗值较实测值偏小,而该低估值可通过在涡流损耗项中添加一磁通密度项方式来补偿[3],如式(3)所示。
PIEM=a1Bαf+a2B2f2(1+a3Ba4)+a5B1.5f1.5
(3)
式中,a1Bαf表示磁滞损耗;a2B2f2(1+a3Ba4)表示涡流损耗,其中磁通密度项(1+a3Ba4)用来计及由饱和因素引起的涡流损耗增加值;a5B1.5f1.5表示异常损耗。但式(3)中各损耗系数均为常系数,且并未考虑由谐波磁场引起的磁滞损耗的变化情况,故无法在频率和磁通密度范围跨度较大时保证模型的准确性。
文献[12]在式(3)基础上考虑了由谐波磁场引起的铁心损耗,提出如式(4)所示计算模型。
(4)
式中,Bn、fn分别为利用有限元计算得到的磁通密度进行傅里叶分解而得到的各次谐波磁通密度的幅值和频率;a2a3Ba4+2f2是由饱和因素引起的涡流损耗增加值。式(4)虽然计及了谐波磁场的影响,但未提出明确的磁滞损耗补偿项。另外,式(4)中各系数均为常系数,仍无法在频率和磁通密度范围跨度较大时保证模型的准确性。
综合上述分析可知,为了能够在较宽频率和磁通密度范围内准确计算铁耗的同时,还可以对损耗进行精细化分析,新建模型需满足以下条件:
1)在考虑铁磁材料非线性特性基础上,系统研究铁耗随磁通密度和频率的变化规律,对涡流和磁滞损耗单独补偿,且补偿项系数应随磁通密度或频率变化而变化。
2)磁通密度和频率变化越大,拟合的病态特性就越严重,为了避免这一问题,可按照频率或磁通密度的大小进行分段,并在每个磁通密度或频率段内采用不同的补偿项系数对磁滞和涡流损耗进行补偿。
2 分段变系数铁耗模型建立
2.1分段变系数计算模型
通过对多种硅钢片大量实测数据分析,发现异常损耗所占总损耗比重较小,为简化模型便于损耗系数求解,本文只重点分析磁滞和涡流两项损耗,进而提出一种分段变系数铁耗模型,即在不同磁通密度和频率范围内,采用不同附加磁通密度项来计及由铁磁材料非线性因素和高次谐波磁场引起的涡流和磁滞损耗增加值。基于前述分析并结合有限元方法,本文提出的分段变系数铁耗计算模型如式(5)所示。
(5)
式中,j为电机有限元模型中第j个单元;Aj为第j个单元的面积;lm为电机铁心材料的有效长度;fn为磁通密度傅里叶分解的第n次谐波的频率;Bn为磁通密度第n次谐波的幅值;kh、ke、ka、α为常系数,其含义与Bertotti模型中相应系数一致。简要说明如下:
1)在定转子铁心不同位置,根据磁通密度和频率的大小不同将磁通密度和频率分成若干区间。式(5)中参数k1n、β1n和k2n、β2n由fn、Bn确定,详细求解见第三节。
2.2考虑旋转磁化后的铁耗模型

(6)
式(6)与式(5)相比,仅在磁滞损耗项增加了旋转磁化补偿系数kr,其大小由椭圆率δ确定。
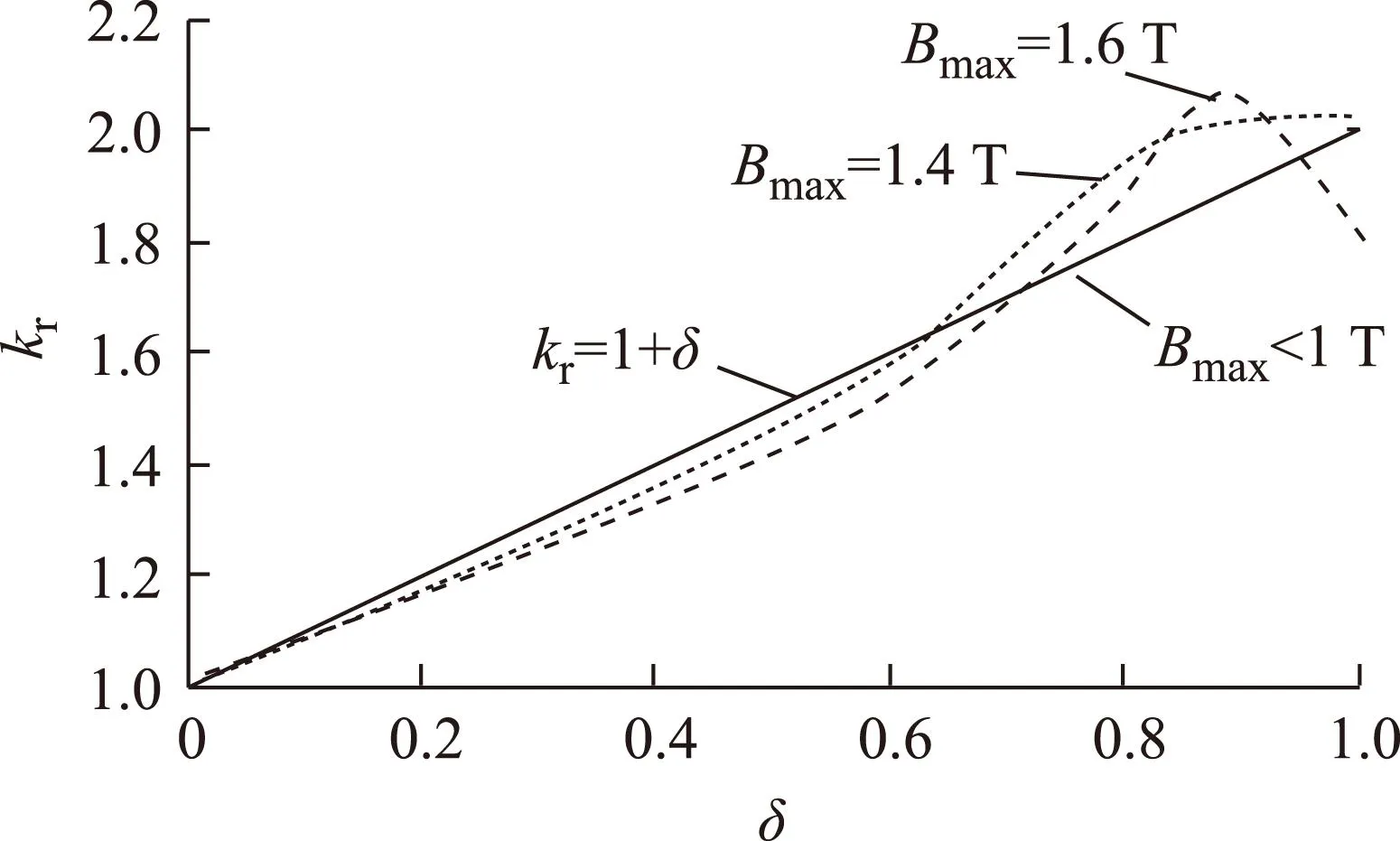
图2 旋转磁化损耗系数kr与磁通密度椭圆率δ的关系Fig.2 The curve of rotation magnetization parameter kr versus ellipticity δ and peak of the flux density
2.3本文所提模型的特点
综上所述,本文所提模型共有9个损耗系数,包含4个常系数(kh、ke、ka和α)和5个变系数(k1、β1、k2、β2、kr),其中k1、β1、k2和β2随磁通密度与频率变化,kr随磁通密度轨迹椭圆率变化。需要指出的是对于不同硅钢片,系数kh、ke、ka、α、k1、β1、k2和β2是不同的,各系数的求解方法将在第三节详细说明。
变系数模型往往通过数值方法将Bertotti模型损耗系数拟合为磁通密度或频率的多项式,但本文所提模型没有改变Bertotti模型损耗系数,而是通过研究谐波磁场与铁磁材料非线性对磁滞和涡流损耗影响的物理本质,在不同磁通密度或频率段引入补偿系数确保模型适用性,其特点为:
1)由于未改变Bertotti模型损耗系数,通过本文所提模型可以直观获得谐波磁场以及铁磁材料非线性对磁滞和涡流损耗的影响规律。
2)模型损耗系数的求解方法更加简单,同时也避免了多项式拟合的病态特性。
3 分段变系数模型损耗系数求解方法
3.1经典Bertotti模型损耗系数的求解
一般来说,仅在较低的频率和磁通密度时,易将磁滞损耗、涡流损耗、异常损耗从总损耗中分离出来[5]。基于此,磁滞和异常损耗系数一般是在磁通密度小于0.2 T、频率低于50 Hz时求解得出,涡流损耗系数ke可由式(2)求出。由于频率和磁通密度较低时,Bertotti三项常系数模型精确度较高,即认为式(1)所求值为实测值,故可用式(7)~式(9)求解异常损耗系数。
(7)
(8)
联立式(7)和式(8),可得
(9)
式中,Pf1、Pf 2分别为频率为f1和f2时不同磁通密度对应铁耗实测值。求解过程中,频率f1和f2、以及磁通密度B应尽可能小(例如f1、f2取5 Hz、10 Hz,B取0~0.2 T)。
求出异常损耗系数后,即可对磁滞损耗系数kh和指数项α进行求解。由式(7)可得
(10)
式(10)两边取对数,可得
(11)
式中,f1为已知量;B为自变量。利用式(11)进行线性拟合求出磁滞损耗系数kh和指数项α。
3.2涡流损耗附加磁通密度高次项系数的求解
对磁通密度和频率分的段数越多,即每个区间的大小越小,模型的精确性越高,但这会增加模型系数的求解难度以及模型的复杂程度。通过对大量硅钢片实测数据分析发现,如果频率区间大小选的合理,求解涡流损耗附加磁通密度项系数时,当磁通密度频率小于400 Hz时,可将磁通密度分为B≤1.2 T、1.2 T
1)当频率f<400 Hz时,铁磁材料磁滞回线畸变较小,即谐波磁场引起的磁滞回线畸变较小,因此在该频率范围内求解涡流损耗附加磁通密度高次项系数,可忽略磁滞损耗变化,即令磁滞损耗附加低次项为1,即认为式(3)所求值为实测值。在此频率范围内,当磁通密度B≤1.2 T时,铁磁材料特性线性度较好,故可不对经典Bertotti三项常系数模型进行补偿;而当磁通密度B>1.2 T时,利用式(12)和式(13)对每个频率段内k2和β2进行求解。
(12)
(13)
联立(12)和式(13),可得
(14)
式(14)两边取对数,可得
ln(D)=ln(k2)+β2ln(B)
(15)
式中,Ptest为给定频率下,磁通密度取不同值时硅钢片损耗实测值。根据式(15),利用线性拟合的方式即可求出各磁通密度和频率段的k2和β2。
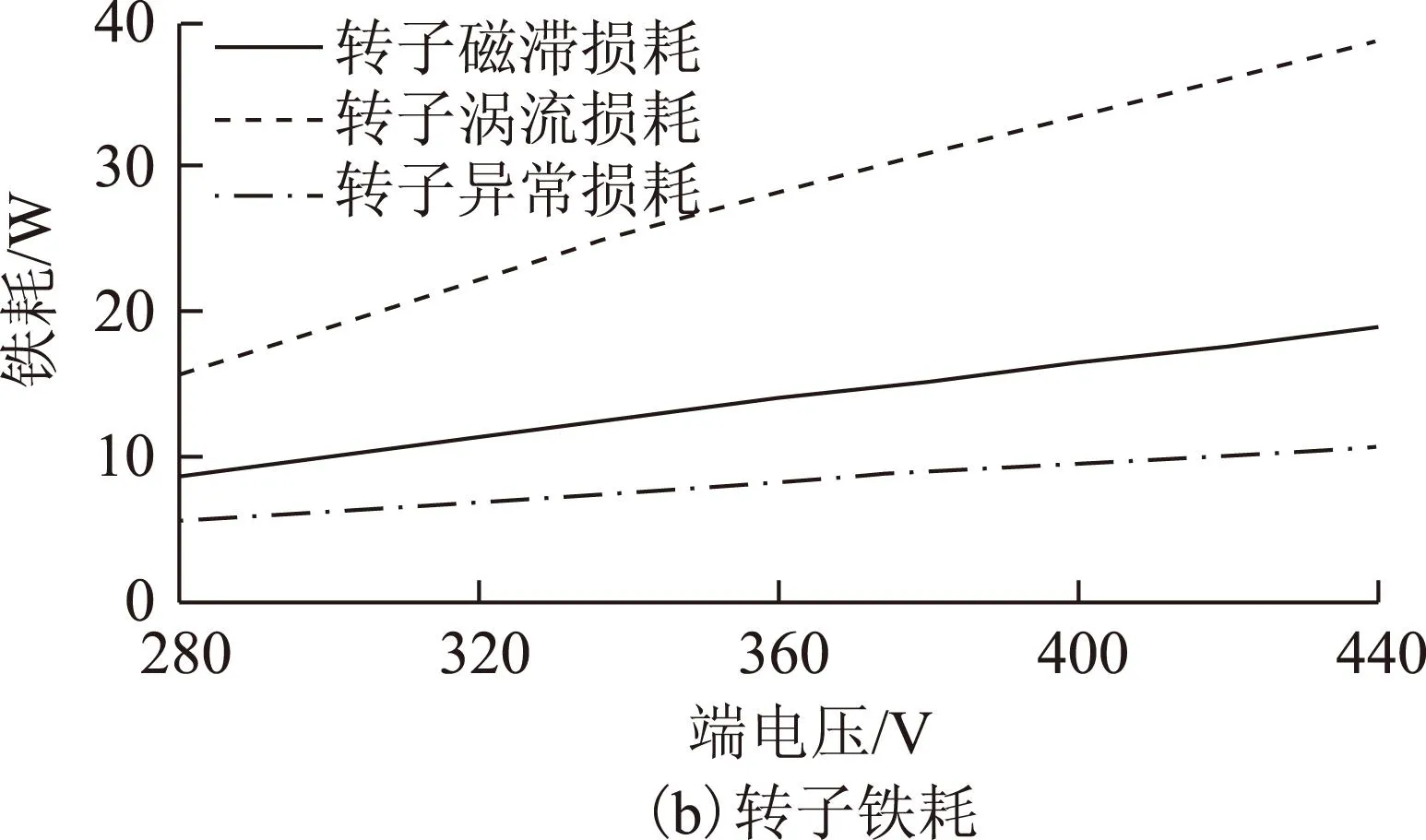
2)当频率f>400 Hz时,经过大量的计算和算法修订并结合文献[5,15]的研究,发现无论铁心磁通密度多大,硅钢片的非线性特性都非常严重。此时可仅使涡流损耗附加磁通密度高次项系数随频率变化,来近似的补偿由电机铁心铁磁材料非线性特性引起的涡流损耗的增加量,如果忽略磁滞损耗变化,利用任意区域的磁通密度求解出的涡流损耗附加磁通密度高次项应大致相等。但该频率范围内的磁滞损耗的变化是不可忽略的,为了排除磁滞损耗变化的影响,应选择磁滞损耗变化尽可能小的区域。为了排除磁滞损耗附加磁通密度低次项的影响,在求解系数时,要使磁滞损耗附加磁通密度项k1Bβ1接近于1。一般来说β1值接近于0,而k1值接近于1,故为了避免磁滞损耗变化的影响,求解涡流损耗附加磁通密度项系数时磁通密度B应接近于1,本文利用磁通密度范围为0.6 T 3.3磁滞损耗附加磁通密度低次项系数的求解 铁磁材料非线性因素引起的附加磁滞损耗主要随频率而变化,本文磁滞损耗附加磁通密度系数仅随频率变化。求解过程为 (16) (17) 联立(16)和式(17),可得 (18) 式(18)两边取对数,可得 ln(E)=ln(k1)+β1ln(B) (19) 同样,根据式(19),利用线性拟合方式可求解出在不同频率段中的k1和β1。 需要说明:当频率f<400 Hz时,式(16)~式(19)中涉及到的涡流损耗附加磁通密度高次项系数k2及β2是在忽略了磁滞损耗附加损耗的情况下得到的,因此在此基础上计算得到的磁滞损耗附加磁通密度低次项系数k1及β1是不准确的。在此频率范围内,磁滞损耗变化不大,一般来说可以忽略,但为了更近一步减少误差,本文仍利用式(16)~式(19)求解出的磁滞损耗附加磁通密度项来对磁滞损耗进行补偿。 3.4损耗系数求解算例 对磁通密度和频率分段的原则是在保证模型准确度的同时频率或磁通密度分的越少越好。磁通密度按照3.2节介绍的方式分段,对于频率则按图3所示的流程来分段。按上述系数求解方法,对型号为DR510和DW470的两种硅钢片在不同磁通密度及频率下的损耗数据进行实测后,进一步对损耗系数进行求解,结果见表1~表4。 图3 对频率区间大小分配的流程Fig.3 The computing method of frequency intervals 损耗系数αkhkeka求解值1.690.0320.000130.000449 表2 硅钢片DR510的涡流损耗附加磁通密度高次项系数和磁滞损耗附加磁通密度低次项系数Tab.2 Additional eddy current higher order coefficients and additional hysteresis losses lower order coefficients of the silicon steel DR510 表3 硅钢片DW470磁滞、涡流及异常损耗系数Tab.3 Loss coefficients of eddy current,hysteresis and excess of the silicon steel DW470 表4 硅钢片DW470的涡流损耗附加磁通密度高次项系数和磁滞损耗附加磁通密度低次项系数Tab.4 Additional eddy current higher order coefficients and additional hysteresis losses lower order coefficients of the silicon steel DW470 从表2和表4可以看出,不同型号硅钢片,涡流损耗附加磁通密度项系数和磁滞损耗附加磁通密度项系数相差非常大。因此对不同型号硅钢片的损耗系数需单独求解。另外,在低频段磁滞损耗变化较小,在高频段其变化较大,说明随着频率升高磁滞回线畸变越来越严重。 4.1实验方案及铁耗实测方法 以Y132S- 4、5.5 kW和YX3-250M- 4、55 kW两台感应电机为例进行实测和仿真对比,所采用的硅钢片分别为DR510和DW470。为了充分反映谐波和非线性因素对铁耗的影响,实测不同电压下的空载运行情况。由于主磁路饱和程度与端电压呈正比,而磁路饱和会引起磁通密度出现明显三次谐波,当定子绕组为角接时,会在绕组中产生明显环流,使电流波形发生畸变现象。所测5.5 kW电机在不同电压下定子绕组电流如图4所示,可以看出电压为220 V时电流接近正弦波,但当电压升至380 V时,受饱和因素影响,电流出现了严重畸变,说明此时非线性程度较严重。因此,对两台电机在不同电压下空载铁耗进行实测与计算对比,可用来验证本文所提模型对不同非线性程度的适用性。测试时空载铁耗测试方法按照GB1032—2012推荐的B法进行。在空载铁耗处理过程中,特别考虑了以下问题: 1)考虑到异步电机空载运行时功率因数较低,采用高精度功率分析仪对不同电压下的空载铁耗进行实测,其相位测量准确度达到0.002 5°,确保低功率因数条件下仍能准确测量输入功率。 2)测试过程中在电机绕组端部安装温度传感器,实时监测电机绕组温升,用于反映温升对定子电阻的影响,进而获得精确定子铜耗。 3)考虑到实测空载铁耗包含转子谐波铜耗,为了得到尽可能真实的铁耗值,利用基于时步有限元的转子铜耗计算方法[24]计算得出不同电压条件下的转子铜耗,进一步在实测铁耗中减去转子铜耗,即可得到实际空载铁耗。 图4 不同电压下5.5 kW电机定子绕组相电流Fig.4 Stator currents of 5.5 kW motor with different voltages 4.2铁耗计算与实测结果对比 利用本文所提模型和Bertotti三项常系数模型分别计算了上述两台电机在不同电压下的空载铁耗值,对比情况如图5和图6所示,可以得出: 1)电压较低时,Bertotti三项常系数模型和本文所提出模型的计算准确度基本一致。例如,5.5kW感应电机在端电压为220 V时,计算得到的转子铜耗为0.98 W,经处理得到实测铁耗值为40.1 W,Bertotti三项常系数模型计算值为34.6 W,本文所提模型计算值为42.2 W,此时,可以看出两种模型计算结果基本一致。 2)随电压升高,Bertotti三项常系数模型和本文所提出模型的计算结果差异较大,与实测铁耗值相比,出现了明显误差。例如,在端电压为380 V时,计算得到的转子铜耗为6.1 W,经处理得到实测铁耗值为128.1 W,Bertotti三项常系数模型计算值为91.9 W,本文所提模型计算值为124.8 W,可以看出本文所提模型计算准确度明显高于Bertotti三项常系数模型。此外,当端电压大于400 V时,本文所提模型计算结果与实测值之间也出现明显差异,这主要是由于本文所提模型无法准确考虑加工工艺、转子导条间横向电流对附加损耗的影响,这些损耗会随电压升高而升高。 图5 5.5 kW电机空载铁耗计算与实测对比Fig.5 Comparison of predicted and tested iron losses of 5.5 kW induction motor 图6 55 kW电机空载铁耗计算与实测对比Fig.6 Comparison of predicted and tested no-load iron losses of 55 kW induction motor 4.3铁耗精细化分析实例 利用本文所提模型同样还可以实现铁耗精细化分析,获得定转子铁心中磁滞、涡流及异常损耗在总铁耗中所占比例。仍以上述两台电机为例,对各项损耗分离后的结果如图7和图8所示。可以看出: 1)感应电机铁耗绝大部分来自于定子,其中各项损耗所占比重从大到小依次为磁滞损耗、涡流损耗、异常损耗。以5.5 kW电机为例,电压为380 V时定子铁耗为91.2 W,占总铁耗的73.1%,其中磁滞损耗为62.3 W,占定子铁耗的68.3%。 2)转子铁耗占总铁耗比重较小,各项损耗所占比重从大到小依次为涡流损耗、磁滞损耗、异常损耗。仍以5.5 kW电机为例,电压为380 V时转子铁耗共33.6 W,其中涡流损耗为22.4 W、占转子铁耗的66.6%。这是由于转子低频磁场对铁耗影响较小,而高次谐波磁场产生的损耗则以涡流损耗为主。 3)无论是定子还是转子,异常损耗所占比重都是最小的。例如,5.5 kW感应电机,端电压为380 V时,定子异常损耗为7.3 W,仅占定子铁耗的8%,转子异常损耗为4.6 W,仅占转子铁耗的13.7%。这与前述第1节中分析一致。 图7 5.5 kW电机空载铁耗精细化分析Fig.7 Analysis of no-load iron losses of 5.5 kW induction motor with different voltages 图8 55 kW电机空载铁耗精细化分析Fig.8 Analysis of no-load iron losses of 55 kW induction motor with different voltages 1)提出一种用于电机损耗精细化分析的分段变系数铁耗计算模型,该模型以经典Bertotti三项常系数铁耗模型为基础,在涡流损耗项中引入涡流损耗附加磁通密度项,在磁滞损耗项中引入磁滞损耗附加磁通密度项,用于考虑磁路饱和导致涡流损耗增加及谐波磁场引起磁滞损耗增加的现象,同时,模型中主要系数均随磁通密度幅值和频率变化,能够很好地反映非线性因素及谐波磁场对铁耗的影响。 2)以Y132S- 4、5.5 kW和Y3-250M- 4、55 kW两台感应电机为例,对其在不同电压下的空载铁耗进行计算和实测对比,并对各项损耗进行精细化分析。结果表明本文所提模型有较高的计算精度和较宽的适用范围。 作为电机损耗精细化分析模型研究的第一步,本文主要针对正弦供电条件下电机内部饱和、齿槽效应及绕组排列产生谐波引起的非线性现象,通过引入相应损耗系数反映上述因素引起的损耗增加;未来研究将重点考虑变频供电条件下由电源谐波与电机内部谐波相互作用产生的复杂物理现象,建立相应的铁耗精确计算模型。 致谢:本文硅钢片损耗的测试工作是在美国Magneforce公司Ren H.Wang博士(IEEE Fellow)大力支持下完成的,在此表示衷心的感谢。 [1]张民,何正友,高仕斌.不同负荷模型下高速铁路牵引供电系统谐波谐振敏感度分析[J].电力系统保护与控制,2015,43(20):21-28. Zhang Min,He Zhengyou,Gao Shibin.Harmonic resonance modal sensitivity analysis for high-speed railway traction supply system considering different harmonic load models[J].Power System Protection and Control,2015,43(20):21-28. [2]郝柱,顾伟,褚建新,等.基于四谱线插值FFT的电网谐波检测方法[J].电力系统保护与控制,2015,42(19):107-113. Hao zhu,Gu Wei,Chu Jianxin,et al.A power network harmonic detection method based on the four-spectrum-line interpolation FFT[J].Power System Protection and Control,2015,42(19):107-113. [3]Bertotti G.General properties of power losses in soft ferromagnetic materials[J].IEEE Transactions on Magnetics,1988,24(1):621-630. [4]佟文明,朱晓锋,贾建国,等.时间谐波对永磁同步电机损耗的影响规律[J].电工技术学报,2015,30(6):60-69. Tong Wenming,Zhu Xiaofeng,Jia Jianguo,et al.Influence law of additional losses induced by time harmonic in permanent magnet synchronous motors[J].Transactions of China Electrotechnical Society,2015,30(6):60-69. [5]Eggers D,Steentjes S,Hameyer K.Advanced iron-loss estimation for nonlinear material behavior[J].IEEE Transactions on Magnetics,2012,48(11):3021-3024. [6]Popescu M,Ionel D M.A best-fit model of power losses in cold rolled motor lamination steel operating in a wide range of frequency and magnetization[J].IEEE Transactions on Magnetics,2007,43(4):1753-1756. [7]Ionel D M,Popescu M,Dellinger S J.On the variation with flux and frequency of the core loss coefficients in electrical machines[J].IEEE Transactions on Industry Applications,2006,42(3):658-667. [8]罗富强,夏长亮,乔照威,等.PWM 激励下异步电机铁耗等值电阻模型[J].电工技术学报,2012,27(7):102-109. Luo Fuqiang,Xia Changliang,Qiao Zhaowei,et al.Model of equivalent iron loss resistance of induction motor fed by PWM[J].Transactions of China Electrotechnical Society,2012,27(7):102-109. [9]佟文明,朱晓锋,朱龙飞,等.不同供电方式对非晶合金永磁同步电机铁耗的影响[J].电工技术学报,2015,30(10):115-122. Tong Wenming,Zhu Xiaofeng,Zhu Longfei,et al.The impact of different supply modes on core losses of amorphous alloy permanent magnet synchronous motor[J].Transactions of China Electrotechnical Society,2015,30(10):115-122. [10]Bagkavos D,Patil P N.Local polynomial fitting in failure rate estimation[J].IEEE Transactions on Reliability,2008,57(1):41-52. [11]Han S H,Jahns T M,Zhu Z Q.Analysis of rotor core eddy-current losses in interior permanent-magnet synchronous machines[J].IEEE Transactions on Industry Applications,2010,46(1):196-205. [12]刘光伟,赵新刚,张凤阁,等.高速永磁爪极电机铁耗与空气摩擦损耗计算[J].电工技术学报,2015,30(2):148-154. Liu Guangwei,Zhao Xingang,Zhang Fengge,et al.Iron loss and air friction loss for high speed permanent magnet claw pole machines[J].Transactions of China Electrotechnical Society,2015,30(2):148-154. [13]Saito T,Takemoto S,Iriyama T.Resistivity and core size dependencies of eddy current loss for Fe-Si compressed cores[J].IEEE Transactions on Magnetics,2005,41(10):3301-3303. [14]Kim H Y,Lee C W.Analysis of eddy-current loss for design of small active magnetic bearings with solid core and rotor[J].IEEE Transactions on Magnetics,2004,40(5):3293-3301. [15]Steentjes S,Von Pfingsten Georg,Hombitzer M,et al.Iron-loss model with consideration of minor loops applied to FE-simulations of electrical machines[J].IEEE Transactions on Magnetics,2013,49(7):3945-3948. [16]Barbisio E,Fiorillo F,Ragusa C.Predicting loss in magnetic steels under arbitrary induction waveform and with minor hysteresis loops[J].IEEE Transactions on Magnetics,2004,40(4):1810-1819. [17]龚宇,崔巍,章跃进.考虑局部磁滞损耗的复合电机铁损耗计算[J].中国电机工程学报,2014,34(30):5395-5400. Gong Yu,Cui Wei,Zhang Yuejin.Iron loss calculation of compound motors considering minor hysteresis losses[J].Proceedings of the CSEE,2014,34(30):5395-5400. [18]Ibrahim M,Pillay P.Core loss prediction in electrical machine laminations considering skin effect and minor hysteresis loops[J].IEEE Transactions on Industry Applications,2013,49(5):2061-2068. [19]Marracci M,Tellini B.Hysteresis losses of minor loops versus temperature in MnZn Ferrite[J].IEEE Transactions on Magnetics,2013,49(6):2865-2869. [20]Hernandez-Aramburo C A,Green T C,Smith A C.Estimating rotational iron losses in an induction machine[J].IEEE Transactions on Magnetics,2003,39(6):3527-3533. [21]Belahcen A,Rasilo P,Arkkio A.Segregation of iron losses from rotational field measurements and application to electrical machine[J].IEEE Transactions on Magnetics,2014,50(2):893-896. [22]Ma L,Sanada M,Morimoto S,et al.Prediction of iron loss in rotating machines with rotational loss included[J].IEEE Transactions on Magnetics,2003,39(4):2036-2041. [23]Gmyrek Z,Boglietti A,Cavagnino A.Estimation of iron losses in induction motors:calculation method,results,and analysis[J].IEEE Transactions on Industrial Electronics,2010,57(1):161-171. [24]赵海森,刘晓芳,杨亚秋,等.基于时步有限元分析的超高效电机定子槽形优化设计[J].中国电机工程学报,2011,31(33):115-122. Zhao Haisen,Liu Xiaofang,Yang Yaqiu,et al.Stator slot optimal design of premium motors based on time-stepping finite element method[J].Proceedings of the CSEE,2011,31(33):115-122. A Piecewise Variable Coefficient Model for Precise Analysis on Iron Losses of Electrical Machines Zhang DongdongZhao HaisenWang YilongXu GuoruiLiu Xiaofang (State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources North China Electric Power UniversityBeijing102206China) This paper proposed a precise iron losses prediction model with piecewise variable coefficients. Based on the Bertotti’s three-term iron loss model,an additional flux density higher-order term and an additional flux density lower-order term are introduced to consider the increased eddy current loss and the local hysteresis loss caused by magnetic saturation and harmonic field,respectively. Meanwhile,the main loss coefficients are varying with the amplitude and frequency of the flux density,through which the influence of the fundamental and harmonic fields on iron losses are considered effectively. At the same time,the hysteresis loss,eddy current loss,and excess loss can also be predicted accurately. To verify the effectiveness of the presented model,the experimental validations are carried out on two induction motors,i.e. Y132S- 4,5.5 kW and YX3-250M- 4,55 kW,under different supply voltages with no-load. Both the presented model and Bertotti’s three-term iron loss model are used to predict the iron losses of the above motors. It reveals that the iron loss predicted by the presented model agree well with the tested ones across a wide voltage ranges. Electrical machines,iron losses,hysteresis,eddy current,non-linear 2015-05-19改稿日期2015-09-06 TM31 张冬冬男,1990年生,硕士研究生,研究方向为交流电机能耗分析。 E-mail:747797459@qq.com 赵海森男,1982年生,博士,副教授,研究方向为电机内电磁场数值计算、电机系统节能及新型节能电机设计。 E-mail:zhaohisen@163.com(通信作者) 国家自然科学基金(51307050)、北京市科技计划项目(Z1411000014007)和中央高校基本科研业务费专项资金(2015ZD03)资助。




4 实验验证
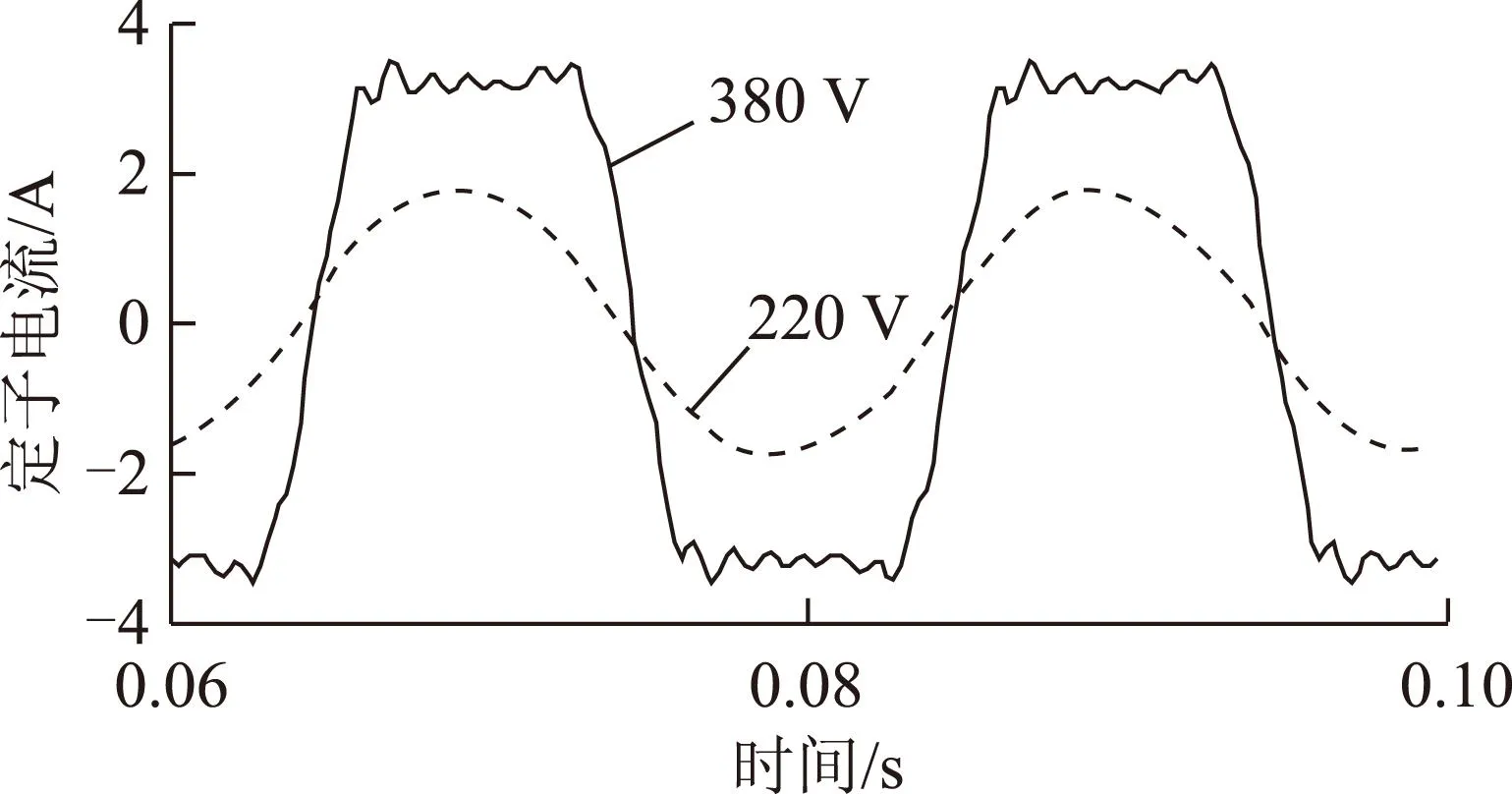
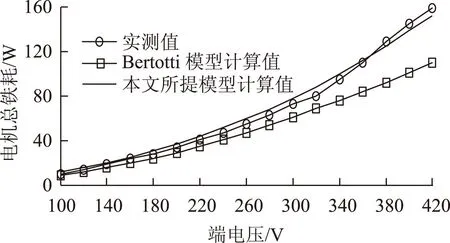



5 结论

