十五相感应电机对称缺相运行时的定子漏抗计算

郑晓钦　王　东

(1.华中科技大学电气与电子工程学院　武汉　430074 2.舰船综合电力技术国防科技重点实验室(海军工程大学)　武汉　430033)



十五相感应电机对称缺相运行时的定子漏抗计算

郑晓钦1王东2

(1.华中科技大学电气与电子工程学院武汉430074 2.舰船综合电力技术国防科技重点实验室(海军工程大学)武汉430033)

定子参数计算是应用等值电路进行多相感应电机对称缺相运行性能分析的基础。通过引入关联矩阵反映所缺相数，分别对定子槽漏抗、谐波漏抗、端部漏抗进行计算，得到了十五相感应电机缺一个五相、两个五相绕组对称工况下的定子漏抗。计算结果表明，对于整距集中绕组的十五相感应电机，缺少五相或十相后，每相槽漏抗不变，谐波漏抗增大，而端部漏抗减小，故对称缺相运行工况下的定子漏抗参数与正常工况下并无明确倍数关系。在正常工况及缺十相对称运行工况下对十五相感应电机原理样机进行了堵转试验，试验测得的短路电抗与计算值相互吻合，间接验证了计算结果的正确性。

十五相感应电机对称缺相运行等值电路定子漏抗

0　引言

近年来，随着船舶电力推进等大功率驱动应用领域的快速发展，多相感应推进电机及其调速系统成为研究热点[1- 4]。相比传统三相电机，多相推进电机具有谐波含量低、转矩性能平稳、可靠性高等诸多优势[5-7]。特别对于十五相推进感应电机，出现定子绕组一相或多相开路故障时，可直接切除含故障相的整个五相甚至十相绕组继续降额运行。但因十五相推进感应电机应用背景特殊，鲜有其对称缺相运行性能分析的报道[8，9]。考虑到定子参数计算是应用等值电路进行性能分析的基础，尤其缺相后的漏抗参数发生了变化，其计算的准确性直接影响电机对称缺相稳态运行与暂态运行性能的分析。

定子漏抗参数包括槽漏抗、谐波漏抗与端部漏抗三部分，文献[10-13]给出了三相电机定子漏抗的计算公式，但这些公式大都不能直接用于多相电机定子漏抗的计算。对于多相电机定子槽漏抗、谐波漏抗与端部漏抗的计算方法，文献[14-20]已经作了较为详细的说明，但都只在对称正常工况下进行计算，均未考虑缺相工况下的漏抗参数计算，也未见有对称缺相运行时定子漏抗参数变化规律的总结。鉴于现有方法在计算不同相数定子漏抗参数时，需根据相数的改变重新列写公式求解，且不同绕组结构下的计算公式也不同，应用到多相电机对称缺相运行参数计算时十分麻烦，故有必要提出一套适用于任意缺相工况下定子漏抗计算的通用方法。

本文从网络图论的基本原理出发，引入反映相绕组与各槽线圈边间及相绕组与各槽线圈间连接关系的关联矩阵，通过关联矩阵中相应元素的变化体现所缺相数，计算了一台45 kW十五相感应电机原理样机在不同对称缺相运行工况下的槽漏抗、谐波漏抗和端部漏抗。所用计算方法通用性强，方便规范统一编程，适用于任意绕组结构的多相感应电机缺相工况下定子漏抗参数计算。

1　十五相感应电机绕组结构

该十五相推进感应电机(电机基本数据参见附录)定子绕组由3个五相绕组组成，每个五相绕组各相互差2π/5电角度，每两个五相绕组间互移π/15电角度，十五相绕组的中点相互独立，构成中点独立的半对称绕组。若十五相中任一相发生开路故障，则可将含故障相的整个故障五相绕组全部切除，剩余十相绕组对称运行；若任意两个五相中同时出现多相绕组开路故障，则可将含故障相的整个十相全部切除降额运行，电机缺相前后绕组分布变化如图1所示。

图1　十五相电机对称缺相运行定子绕组变化Fig.1　Stator windings change of 15-phase inductance motor under symmetrical fault condition

对于缺相后的感应电机，定子绕组分布仍然对称，但各参数均已发生了变化。因此，在进行电机对称缺相运行性能分析时必须考虑缺相引起的定子漏抗变化。下面具体介绍定子各部分漏抗缺相后的计算方法及变化规律。

2　定子槽漏抗计算

该十五相感应电机定子采用半开口矩形槽，故槽比漏磁导计算较为简单。图2给出了定子槽型，可分为两部分，即槽口与槽楔部分和槽身部分。

图2　定子半开口槽Fig.2　Stator semi-opening slot

计算过程中所做假设条件为：①电流在导体截面上均匀分布；②忽略铁心磁阻不计，槽漏磁动势全部消耗在槽中；③定子槽中所有磁力线与电枢表面平行。

设上、下层线圈边中串联导体数均为W，则上层线圈边的自感Ms11、下层线圈边的自感Ms22、上下层线圈边的互感Ms12分别为

(1)

式中，λ11为相应于上层线圈边自感的槽自比漏磁导；λ22为相应于下层线圈边自感的槽自比漏磁导；λ12为相应于上下层线圈边互感的槽互比漏磁导，其值可根据文献[7]直接写出

(2)

在由式(1)、式(2)计算各相槽漏感时，为能将缺相工况与正常工况下的相间绕组关系进行统一表示，清楚地反映15相感应电机定子绕组15个槽自漏感与相间210个槽互漏感(只计算105个即可)在缺相前后的关系，引入相绕组与各槽线圈边间的关联矩阵B。仿照电路网络中列写回路与支路关联矩阵的方法，将每槽线圈边当成一条支路，每相绕组当成一个回路。当各相绕组回路电流方向与每槽线圈边支路电流方向一致时，B中对应元素为1，二者方向相反时对应元素为-1，无关联时则用0表示。由于原理样机定子槽数为60，每相绕组均分上下两层线圈边，故关联矩阵B为30×60阶。

图3为a1相绕组一对极下的绕组连接，并规定了线圈边电流正方向以及绕组回路电流正方向(由x1端流入，a1端流出)。

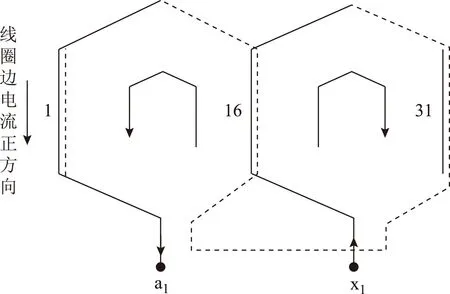
图3　线圈边电流正方向以及绕组回路电流正方向Fig.3　Positive direction of coil edge and winding loop currents

其余各相绕组与a1相连接方式相同，这里不再一一画出。根据图中规定的线圈边电流正方向及各相绕组电流方向，可列写相绕组与各槽线圈边间的关联矩阵B。若按a1相下、上层边，b1相下、上层边，c1相下、上层边，…，直到e3相下、上层边的顺序列写，并考虑到每相中二对极下的元素相同，则十五相正常工况下的关联矩阵B可写为

式中，B1、B2、B3均为10×30阶子矩阵，分别对应a1～e1、a2～e2以及a3～e3五相绕组一对极下元素。

例如，B1中第1、2行为对应a1相一对极下的元素，其值为

当发生绕组开路故障后，只需将矩阵中相应开路相的元素变为0即可。因此，电机在十相对称缺相运行(缺五相)工况下的关联矩阵B为

五相对称缺相运行(缺十相)工况下的关联矩阵B为

可以看出，无论正常工况亦或对称缺相运行工况，关联矩阵B均为30×60阶矩阵，只是所缺相元素变为0而已，故列写过程简单灵活。

设b[(2m-2+i)，k]和b[(2n-2+j)，k]分别为B中第2m-2+i行、第k列和第2n-2+j行、第k列元素，可得第m相与第n相间槽漏感为

(3)

式中，m=1，2，3，…，15；n=1，2，3，…，15；当m=n时，即为每相槽自漏感。

由式(3)得到的各相槽漏感为15×15阶矩阵，包括15个槽自漏感及105个槽互漏感。可进一步以a1相为基准对每相槽漏抗进行折算，得到电机对称运行情况下考虑所有相绕组共同作用时的定子每相槽漏抗为

(4)

式中，Ls[1，5(k-1)+i]为a1相绕组的槽自漏感及与其他各相的相间槽互漏感，H。

根据式(1)～式(4)计算了十五相感应电机正常运行及不同对称缺相运行时的槽漏抗，见表1。

表1　整距绕组不同缺相工况下槽漏抗Tab.1　Slot leakage reactance of full-pitch stator winding under different symmetrical faultconditions

由于原理样机定子采用整距集中绕组，同槽中上、下层线圈边均属同相绕组，相间槽互漏抗均为0，因此即使在对称缺相工况下，剩余各相槽漏抗仍保持不变。若定子采用短距绕组，则相间槽互漏抗不再为0，缺相后各相槽漏抗会发生改变。为证明绕组结构对缺相前后各相槽漏抗的影响，利用现有原理样机结构尺寸，将短距比人为改为13/15，为与整距集中绕组下的关联矩阵对比，同样给出了子矩阵B1中对应a1相一对极下的元素。

根据修改后的关联矩阵重新计算了短距绕组时不同对称缺相运行工况下的相槽漏抗，结果见表2。

表2　短距绕组不同缺相工况下槽漏抗Tab.2　Slot leakage reactance of short-pitch stator winding under different symmetrical fault conditions

由表2计算结果可看出，十五相电机在十相和五相对称缺相运行工况下，由于缺相引起相间槽互漏抗的减少，最终导致各相槽漏抗发生变化。因此，定子绕组结构不同，多相电机对称缺相运行工况下的各相槽漏抗变化情况也不同。而无论何种绕组结构，在何种缺相故障工况下，均可通过关联矩阵B清晰有效地反映相绕组与各槽线圈边间的连接关系。

3　定子谐波漏抗计算

为统一计算不同工况下的各相谐波漏抗，先以单一线圈为基础，通过总电感减去基波电感的方法计算两线圈间的谐波电感，对于本文原理样机60个定子槽中的任意两槽线圈间的谐波漏感可按文献[16]中的方法计算，本文不再赘述。与相间槽漏抗计算方法相似，这里引入相绕组与各槽线圈间的关联矩阵C，计算不同对称缺相运行工况下的各相谐波漏抗。

同样将每槽线圈当成一条支路，每相绕组当成一个回路，列写每相绕组在整个2对极下所有线圈的分布情况，即15×60阶矩阵。图4仍以一对极下的a1相绕组为例，给出了线圈电流正方向及相绕组电流方向。

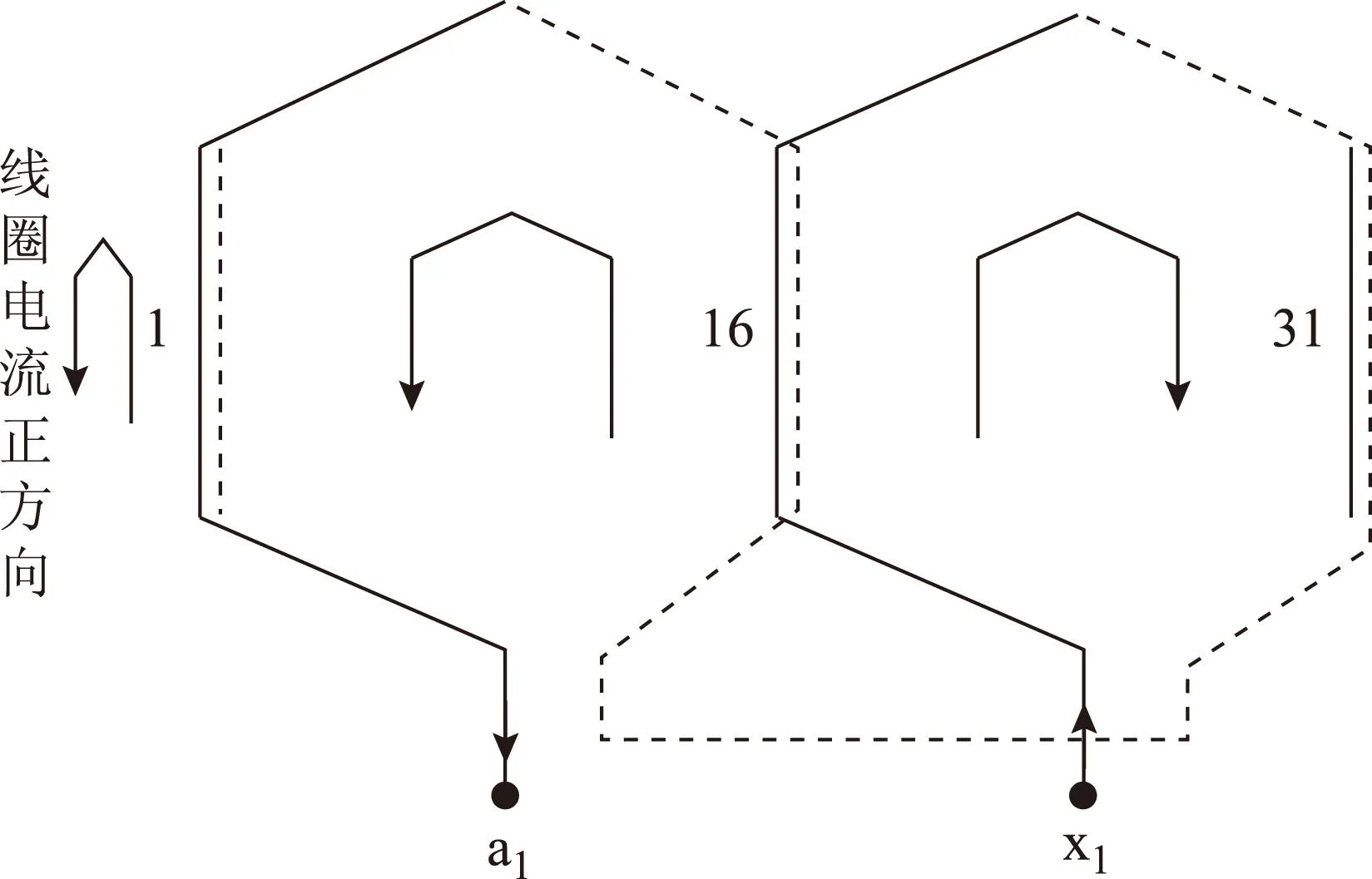
图4　线圈电流正方向及相绕组电流方向Fig.4　Positive direction of coil and winding loop currents

按a1相、b1相、c1相、…、e3相的排序进行列写，则十五相正常工况下的关联矩阵C可写为

式中，C1、C2、C3均为5×30阶子矩阵，分别对应a1～e1、a2～e2以及a3～e3五相绕组一对极下元素。

例如，C1中对应a1相一对极下的元素为

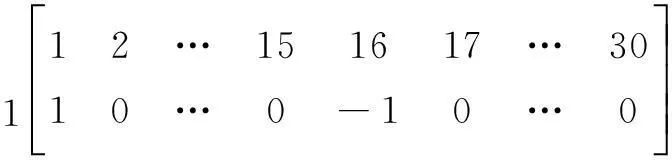
设c(m，i)和c(n，j)分别为C中第m行、第i列和第n行、第j列元素，则第m相与第n相间谐波漏感为

(5)

式中，Mh(i，j)为第i线圈与第j线圈间的谐波电感，H。

同理，在求得15×15阶各相谐波漏感矩阵后，以a1相为基准进行折算，则考虑所有相绕组共同作用时的定子每相谐波漏抗为

(6)

根据式(5)、式(6)分别计算了十五相感应电机正常运行及不同对称缺相运行时的相谐波漏抗，结果如表3所示。

表3　整距绕组不同缺相工况下谐波漏抗Tab.3　Harmonic leakage reactance of full-pitch stator winding under different symmetrical fault conditions

由表3中计算结果可看出，随缺相数量的增加，各相谐波漏抗逐渐增大。这是由于谐波漏抗为各次谐波磁场所感生的基频电动势对应的电抗，其大小与气隙中谐波磁动势的多少密切相关。定子相数减少，对称电流在气隙中产生的谐波旋转磁动势增多，相应的各相谐波漏抗会随之增大。此外，谐波漏抗大小还与绕组连接方式相关，即当电机相数一定时，整距集中绕组与短距分布绕组的各相谐波漏抗也不相同。其差别体现在第i线圈与第j线圈间的谐波电感Mhij中，而整距绕组与短距绕组的关联矩阵C均相同。为证明绕组结构对缺相前后各相谐波漏抗的影响，同样利用现有原理样机尺寸，计算了短距比为13/15时不同对称缺相运行工况下的相谐波漏抗，结果见表4。

表4　短距绕组不同缺相工况下谐波漏抗Tab.4　Harmonic leakage reactance of short-pitch stator winding under different symmetrical fault conditions

对比表3、表4计算结果可看出，短距绕组对谐波漏抗有明显削弱作用，且相数越少削弱作用越明显。而在15相电机正常工况下，由于本身谐波含量较低，因此短距绕组结构无太明显优势。

4　定子端部漏抗计算

本文在计算端部漏感时仍沿用文献[14，17]中的思路，引入气隙电流和镜像电流，以Biot-Savart定律为基础，将线圈端部各大段分成若干小段，用数值方法计算两线圈间端部电感。同样通过相绕组与各槽线圈间的关联矩阵C可求得第m相与第n相间端部漏感为

(7)

式中，Me(i，j)为第i线圈与第j线圈间的端部电感，H。

与各相槽漏抗和谐波漏抗计算类似，最终折算为所有相绕组共同作用时的定子每相端部漏抗。表5为十五相感应电机正常运行及不同对称缺相运行时的端部漏抗。

表5　整距绕组不同缺相工况下端部漏抗Tab.5　End-winding leakage reactance of full-pitch stator winding under different symmetrical fault conditions

由表5中计算结果可看出，随相数的减少，各相端部漏抗明显减小，但由于受线圈端部所跨机械角度等因素影响[17]，其大小变化与相数间并无明确的反比关系存在，而与绕组的短距比密切相关，故绕组连接方式也会对不同缺相工况下的端部漏抗产生影响。表6为短距比为13/15时不同对称缺相运行工况下的各相端部漏抗。

表6　短距绕组不同缺相工况下端部漏抗Tab.6　End-winding leakage reactance of short-pitch stator winding under different symmetrical fault conditions

综合表5、表6中的计算结果，无论是整距集中绕组还是短距分布绕组，缺相后各相端部漏抗均随相数的减少而减小。

5　计算结果的间接试验验证

根据上述计算结果可得到十五相感应电机在不同对称缺相运行工况下的定子漏抗，由于堵转试验所测得漏电抗为定、转子漏抗之和，无法再将二者进行分离，所以试验只能间接验证定子漏抗计算结果。

现对45 kW十五相感应电机原理样机进行堵转试验，分别测量电机十五相运行与五相运行时的短路漏抗，即定、转子总漏抗。试验中，电机由十五相变频器供电，调制方式采用基于载波层叠的PWM脉宽调制，由录波仪同时采集定子a1～e1、a2共6相电压、电流数据。对录波仪采集的各相电压、电流进行Fourier分解，得到基波电压U1、基波电流I1及两者间的相位差，进而可求得各相基波短路漏抗，最终将6相的基波短路漏抗平均值作为电机的基波堵转漏抗。表7为不同相数工况下短路漏抗的计算值与实测值对比。

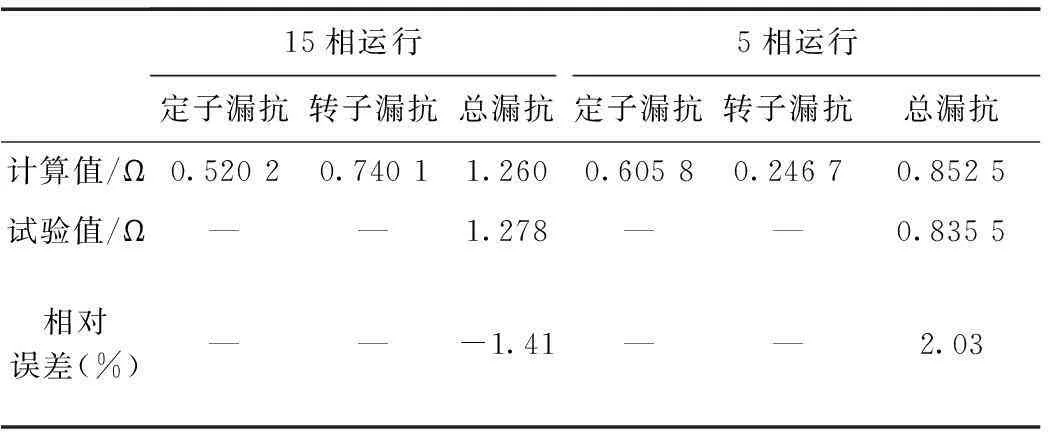
表7　不同缺相工况下短路漏抗结果对比Tab.7　Calculated and measured short-circuit reactances under different conditions

表7中定子漏抗计算值为表1、表3、表5中各相槽漏抗、谐波漏抗与端部漏抗之和。笼型转子漏抗采用传统方法[21，22]求得，只是在剩余5相对称缺相运行时，向定子绕组折算系数变为15相正常工况时的1/3。从表中的对比结果可知，最大误差仅为2.03%，说明不同工况下的总漏抗计算值较为准确。

6　结论

本文以一台45 kW十五相感应电机原理样机为例，通过引入相绕组与各槽线圈边间的关联矩阵及相绕组与各槽线圈间的关联矩阵，分别计算了电机在正常工况下及十相、五相对称缺相运行工况下的定子各相槽漏抗、谐波漏抗和端部漏抗。计算方法不仅适用于多相电机在对称缺相运行工况下的定子漏抗计算，同样适用于不对称缺相运行工况。只是在不对称缺相运行工况下，定子各相电流不再对称，故无需再折算为考虑所有相绕组共同作用时的每相漏抗，只需通过关联矩阵求得各线圈间的互感矩阵即可。在应用关联矩阵计算不同工况定子漏抗时无需重新编程，只通过关联矩阵中相应元素的变化体现相数的变动即可，计算过程简便清晰，具有较强的通用性。

鉴于整距集中绕组同槽中上、下层线圈边均属同相绕组，只存在槽自漏抗，相间槽互漏抗均为0，故各相槽漏抗不随相数改变而改变。而短距分布绕组同槽中的两层线圈可能属于不同相绕组，相间槽互漏抗不再为0，因此各相槽漏抗会随相数的减少而改变。

由于电机相数与空间旋转磁动势次数密切相关，相数越少，多相对称电流在气隙中产生的谐波旋转磁动势越多，故在对谐波磁动势无任何削弱作用的整距集中绕组中，各相谐波漏抗会随缺相数量的增多而大幅增加，而对于短距分布绕组来说，各相谐波漏抗在缺相后的增量要明显减小。

在各相端部漏抗的计算过程中，由于涉及与绕组短距比相关的线圈端部所跨机械角度等量，因此绕组连接方式也会对不同缺相工况下的端部漏抗产生影响，但总体变化趋势相同，均随缺相数量的增多而减小。

综合各相槽漏抗、谐波漏抗和端部漏抗的变化趋势，各相定子总漏抗在电机对称缺相运行时的变化并无规律可循，通过本文中方法可方便的计算不同缺相工况下的定子漏抗。通过对原理样机的堵转试验，测得电机十五相正常工况与五相对称缺相运行工况下的短路电抗，与计算得出的电机定转子总漏抗进行对比，两者误差较小，从而间接验证了本文在计算十五相电机对称缺相运行工况下定子漏抗过程中所用方法的准确性。

附录

样机参数：

1)样机数据：额定功率PN=45 kW；相数m=15；极对数p=2；额定相电压(基波)UN=140 V；额定相电流(基波)IN=25 A；基波频率f=20 Hz。定子槽数Z1=60；定子采用双层整距集中绕组，线圈单层匝数N=12，每相串联总匝数W=48；并联支路数A=1。转子槽数Z2=38；转子采用直槽笼型转子。

2)定子槽型尺寸：槽口宽b0=5.4 mm；槽宽b1=9.3 mm；槽口高h0=1 mm；槽楔高h1=3 mm；单层绕组高h2=h4=20 mm；层间绝缘垫条高h3=2.5 mm。

[1]Jones M，Vukosavic S N，Dujic D，et al.A synchronous current control scheme for multiphase induction motor drives[J].IEEE Transactions on Energy Conversion，2009，24(4)：860-868.

[2]Tani A，Mengoni M，Zarri L，et al.Control of multi-phase induction motors with an odd number of phases under open circuit faults[J].IEEE Transactions on Power Electronics，2012，27(2)：565-577.

[3]Apsley J M.Derating of multiphase induction machines due to supply imbalance[J].IEEE Transactions on Industry Applications，2010，46(2)：798-805.

[4]Abdel-Khalik A S，Morsy A，Ahmed S，et al.Effect of stator winding connection on performance of five-phase induction machines[J].IEEE Transactions on Industrial Electronics，2014，61(1)：3-19.

[5]杨家强，高健，金玉龙，等.基于矢量控制的多相感应电机电子变极调速技术[J].电工技术学报，2014，29(3)：96-102.

Yang Jiaqiang，Gao Jian，Jin Yulong，et al.Electronic pole-changing speed adjusting technology of multiphase induction motors based on vector control[J].Transactions of China Electrotechnical Society，2014，29(3)：96-102.

[6]袁飞雄，黄声华，龙文枫.六相永磁同步电机谐波电流抑制技术[J].电工技术学报，2011，26(9)：31-36.

Yuan Feixiong，Huang Shenghua，Long Wenfeng.Techniques to restrain harmonics of six-phase permanent magnet synchronous motors[J].Transactions of China Electrotechnical Society，2011，26(9)：31-36.

[7]纪锋，王公宝，付立军，等.十二相同步发电机降阶等效模型研究[J].电力系统保护与控制，2012，40(2)：28-33.

Ji Feng，Wang Gongbao，Fu Lijun，et al.Study on equivalent reduced model of twelve-phase synchronous generator[J].Power System Protection and Control，2012，40(2)：28-33.

[8]陈林.十五相感应电机定子绕组多相开路的稳态特性[J].电工技术学报，2004，19(11)：14-19.

Chin Lin.Steady state performance of a 15-phase induction machine with multiphase stator windings open circuited[J].Transactions of China Electrotechnical Society，2004，19(11)：14-19.

[9]刘自程，郑泽东，彭凌，等.船舶电力推进中十五相感应电机同轴运行及容错控制策略[J].电工技术学报，2014，29(3)：65-74.

Liu Zicheng，Zheng Zedong，Peng Ling，et al.Fixed joint double fifteen-phase induction motor control and fault-tolerant control in ship propulsion system[J].Transactions of China Electrotechnical Society，2014，29(3)：65-74.

[10]陈世坤.电机设计[M].2版.北京：机械工业出版社，1990：50-62.

[11]程福秀，林金铭.现代电机设计[M].北京：机械工业出版社，1993：155-156.

[12]Boldea I，Nasar S A.The induction machines design handbook[M].Second Edition.Boca Raton：CRC Press，2010：119-139.

[13]Boglietti A，Cavagnino A，Lazzari M.Computational algorithms for induction-motor equivalent circuit parameter determination—part Ⅰ：resistances and leakage reactances[J].IEEE Transactions on Industrial Electronics，2011，58(9)：3723-3733.

[14]王东，吴新振，马伟明，等.非正弦供电十五相感应电机定子漏抗计算[J].中国电机工程学报，2010，30(6)：41- 47.

Wang Dong，Wu Xinzhen，Ma Weiming，et al.Calculation of stator leakage reactances of fifteen-phase induction motor with non-sinusoidal supply[J].Proceedings of the CSEE，2010，30(6)：41- 47.

[15]吴新振，王祥珩.12/3相双绕组异步发电机定子槽漏抗的计算[J].中国电机工程学报，2007，27(12)：46-51.

Wu Xinzhen，Wang Xiangheng.Calculation of stator slot leakage inductance for 12/3-phase dual-winding induction generator[J].Proceedings of the CSEE，2007，27(12)：46-51.

[16]吴新振，王祥珩.12/3相双绕组异步发电机定子谐波漏抗的计算[J].中国电机工程学报，2007，27(21)：71-75.

Wu Xinzhen，Wang Xiangheng.Calculation of stator harmonic leakage inductance for 12/3-phase dual-winding induction generator[J].Proceedings of the CSEE，2007，27(21)：71-75.

[17]吴新振，王祥珩.12/3相双绕组异步发电机定子端部漏抗的计算[J].中国电机工程学报，2007，27(24)：80-84.

Wu Xinzhen，Wang Xiangheng.Calculation of stator end-winding leakage inductance for 12/3-phase dual-winding induction generator[J].Proceedings of the CSEE，2007，27(24)：80-84.

[18]王善铭，王祥珩，李义翔，等.交直流混合供电发电机定子绕组端部漏电感的计算[J].电工技术学报，2001，16(2)：1-5.

Wang Shanming，Wang Xiangheng，Li Yixiang，et al.Calculation of stator end winding leakage inductance synchronous generators with AC and DC stator connections[J].Transactions of China Electroechnical Society，2001，16(2)：1-5.

[19]李槐树，李朗如.多相交流电机端部漏感系数的计算与测量[J].华中理工大学学报，2000，28(9)：34-37.Li Huaishu，Li Langru.The calculation and measurement of end-winding leakage inductance of multiphase electric machines[J].Journal of Huazhong University of Science and Technology，2000，28(9)：34-37.

[20]佟文明，吴胜男，安忠良.基于绕组函数法的分数槽集中绕组永磁同步电机电感参数研究[J].电工技术学报，2015，30(13)：150-157.

Tong Wenming，Wu Shengnan，An Zhongliang.Study on the inductance of permanent magnet synchronous machines with fractional slot concentrated winding based on the winding function method[J].Transactions of China Electrotechnical Society，2015，30(13)：150-157.

[21]付丰礼，唐孝镐.异步电动机设计手册[M].北京：机械工业出版社，2002：42-51.

[22]Boldea I，Nasar S A.The induction machine handbook[M].Boca Raton：CRC Press，2002：137-162.

Calculation of Stator Leakage Reactance of Fifteen-Phase Induction Motor Under Symmetrical Fault Condition

Zheng Xiaoqin1Wang Dong2

(1. College of Electrical and Electronic EngineeringHuazhong University of Science and Technology Wuhan430074China 2. National Key Laboratory for Vessel Integrated Power System Technology Naval University of EngineeringWuhan430033China)

To analyze the operation performance of multiphase induction motors under symmetrical fault condition，the stator leakage reactance in the equivalent circuit should be predicted. The stator slot leakage reactance，harmonic leakage reactance and，end-winding leakage reactance of the fifteen-phase induction motor are analyzed using an incidence matrix model to reflect the five-phase and ten-phase open-circuited fault operation. The analysis results indicate that the stator slot leakage reactance is unchanged and the harmonic leakage reactance is increased，while the end-winding leakage reactance is reduced for fifteen-phase induction motor with full-pitch concentrated stator winding under five-phase and ten-phase open-circuited conditions. Thus，there is no exact integer relationship of the stator leakage reactance between symmetrical fault and normal condition. The short-circuit reactances of a prototype fifteen-phase induction motor are measured with locked-rotor test under normal and ten phases opened-circuited conditions. The analytically predicted results are compared with the measured results，where good agreements are achieved.

Fifteen-phase induction motor，symmetrical fault condition，equivalent circuit，stator leakage reactance

2015-04-24改稿日期2015-10-01

TM343

郑晓钦女，1985年生，博士研究生，研究方向为多相感应电机运行性能分析。

E-mail：zhengxiaoqin619@sina.com

王东男，1978年生，教授，博士生导师，研究方向为电力推进、独立电源系统等。

E-mail：wangdongl@vip.sina.com(通信作者)

国家重点基础研究发展(973)计划(2013CB035601)和国家自然科学基金(51222705，51207163)资助项目。