基于热力耦合的单磨粒临界磨削仿真分析
吴书安,祝锡晶,郭策
(中北大学 机械与动力工程学院,太原 030051)
磨削加工是精密加工中一种重要的方法。在磨削加工的仿真研究中,单磨粒磨削作为砂轮磨削的一种简化形式,近年来受到越来越多学者的重视[1—2]。SU等[3]采用自适应网格划分技术,建立了一种粒尖为四凌锥切刃的单磨粒磨削模型。张明等[4]使用Deform-2D软件建立单磨粒磨削平面仿真模型,分析了磨粒前角与磨削力和工件表面温度之间的关系。在磨削中,材料的塑性去除能实现工件表面更低粗糙度和更好表面质量的要求[5]。BIFANO等[6]最早研究磨削过程的塑性加工临界条件,认为当磨粒切削深度小于其临界磨削深度时,可以实现脆性材料的塑性去除。言兰等[7]通过数值仿真研究不同工艺参数下单磨粒耕犁和磨削的临界磨削转变过程,得到不同切削速度下的临界转变切削深度。磨削时由工件与磨粒接触面摩擦产生的热量会对磨削过程有一定的影响[8]。HUO等[9]对单磨粒实现硅材料的脆-塑转变做了一定的研究,并分析了磨削热对磨削过程的影响。
Ti6Al4V合金具有比强度高和疲劳强度高等良好性能,在航空航天发动机和医疗器械等方面得到广泛应用。在这些应用场合,迫切需要运用更高表面质量和更低粗糙度的零部件。目前,尚未见针对Ti6Al4V合金材料受磨粒刃圆半径和磨削深度共同作用下实现临界磨削的研究。本文基于热力耦合模型,针对单磨粒的不同刃圆半径和磨削深度,对单磨粒实现材料的临界磨削进行仿真研究。
1 仿真模型的建立
1.1 正交微磨削过程仿真
考虑磨粒整体形状的不规则性[10],将磨粒顶尖简化成圆锥角为2θ的圆锥体。磨削时,磨粒顶尖会被部分磨损。将其等效为带有刃圆半径为r的圆锥体,磨削深度为h,如图1所示。
在磨削过程中,磨粒的圆锥角为30°。磨粒采用刚体模型并划分三角形网格单元,网格划分如图2a所示。刃圆半径r=0.1 μm和1 μm时,工件的几何尺寸为 34 μm×10 μm,圆弧段半径为 6 μm;刃圆半径r=10 μm时,工件的几何尺寸为340 μm×100 μm,圆弧段半径为60 μm。对工件划分四边形网格单元,网格划分如图2b所示。工件模型的上边和左右两边均采用密度偏离撒种,得到网格总单元数为4925,总结点数为5148。
微切削中,许多研究者用实验证明:当材料变形尺寸减小到一定值时,有效流动应力发生显著尺度效应的现象。运用应变梯度塑性理论建立的工件材料本构模型,能成功模拟该实验现象。
考虑磨削时磨粒与工件接触表面的热传递,设置传热系数为0.9[11]。建立热-力耦合的正交微磨削有限元模型,假设条件为[12]:磨粒的磨削瞬间被视为平面切削过程;磨削过程为稳态切削;磨削温度不足以使材料有金相组织等变化;刀具被约束为刚体。
基于应变梯度塑性理论的材料有效流动应力计算公式为[12]:
式中:A、B、C、m、n、αC为材料系数,其中[13]C=0.014,m=0.466,n=0.71;G为剪切模量;b为伯格斯常量;分别为有效应变和有效应变率;η为有效应变梯度;σJC为用 Johnson-Cook模型计算的有效流动应力;T为量纲温度项。
运用 ABAQUS/Explicit有限元软件对正交微磨削过程进行仿真。约束工件其余三条边x和y方向的位移自由度。给刀具设定一参考点,并添加运动速度约束,数值大小为60 m/min。微磨削摩擦模型采用罚函数摩擦模型,摩擦因数为 0.5。工件和磨粒材料参数如表1所示[14]。

表1 工件和磨粒材料参数Table1 Material parameters of workpiece and grain
1.2 条件模型的建立
材料在有效流动应力达到屈服极限之前发生弹性变形,无切屑产生;有效流动应力超过材料强度极限时开始有微裂纹产生,并发生塑-脆转变。因此,针对Ti6Al4V合金材料塑性去除的条件模型为:σ≤δ0σs0,不产生切屑;δ0σs0<σ≤δ1σsm,塑性去除阶段;δ1σsm<σ,脆性去除阶段。其中,δ0为单磨粒磨削时塑性域系数,δ1为单磨粒磨削时脆性域系数[15]。具体确定均需要进行大量实验数据分析统计。
2 结果分析
针对单元编号2476的有效流动应力和其右上角的节点编号2601的磨削温度,分析这两个变量受磨粒刃圆半径和磨削深度的影响。单磨粒磨削仿真模型图(图3)中,有效流动应力沿磨粒头周向分布,同一圆弧线上数值相同;离磨粒头部圆弧面越远,工件的有效流动应力越小。这验证了吴继华等[12]所得的结论。
改变单磨粒磨削深度h与刃圆半径r的数值大小,仿真结果如图4所示。图4a、b、c为相同刃圆半径下不同磨削深度对磨削的影响;图4c、d为相同磨削深度下不同刃圆半径对磨削的影响。
针对磨削时的临界脆-塑转变现象和热效应,具体从以下三种条件分析切屑根部所取单元和节点的有效流动应力最大值(σmax)及磨削温度最大值(Tmax)的变化情况。
1)r=0.1 μm。h取 6组数值,仿真得出σmax和Tmax,如表2所示。绘制折线图,如图5所示,σmax先增大后减小。拟合可得,当h≈0.17 μm时,σmax达到最大值,为1009.53 MPa,并出现了尺度效应所体现的“越小越强”现象。Tmax随着h增大而近似呈线性增大。参考条件模型可得:工件材料基本处于脆性分裂阶段。由表1可知,Ti6Al4V合金的强度极限σsm=923.2 MPa。拟合可得,在r=0.025 μm时,实际塑性去除的有效流动应力数值可能大于塑-脆转变的临界值δ1σsm。当h≈0.17 μm 时,磨削热的热软化效应开始对切屑根部材料的有效流动应力产生主要影响。这是由于磨削温度超过了Ti6Al4V合金的动态重结晶温度[14],此时材料内部发生晶粒位错的重新排布,阻碍切屑根部局部塑性变形的阻力下降,出现应力软化现象。继续增大h,由数据拟合可知,当h超过0.33 μm时,流动应力数值可能小于塑-脆转变的临界值δ1σsm,从而实现材料的脆-塑性临界转变。

表2 各变量值(r=0.1 μm)Table2 Value of each variables (r=0.1 μm)
2)r=1 μm。h取 6组数值,仿真得出σmax和Tmax,如表3所示。绘制折线图,如图6所示。拟合可得,当h≈0.5 μm 时,σmax有最小值,为 948.479 MPa;继续增大h,当h≈2.6 μm 时,σmax取得最大值,为998.176 MPa。热软化效应对σmax的影响不明显。参考条件模型可得:切屑基本处于脆性分裂阶段,这将引起工件表面锯齿状的形成,增加磨削过程对磨粒的震荡冲击,不利于工件表面质量的提高,并会降低磨粒的使用寿命。
3)r=10 μm。h取6组数值,仿真得出σmax和Tmax,如表4所示。绘制折线图,如图7所示。σmax随着h的增大,先快速降低再减缓,继续增大h会出现最小值。在h范围内,最小有效流动应力为720.352 MPa,最大为763.59 MPa。而Tmax继续增大,当超过Ti6Al4V合金的动态再结晶温度后,晶粒位错重排,出现的热软化效应促进σmax的进一步降低。参考条件模型可得:切屑的形成均处于塑性流动阶段,这有利于减少磨粒的磨损。
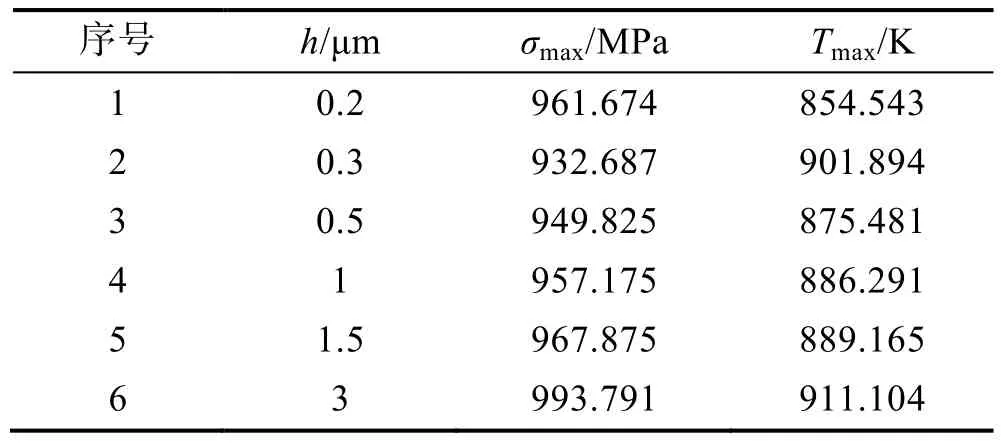
表3 各变量值(r=1 μm)Table3 Value of each variables (r=1 μm)

表4 各变量值(r=10 μm)Table 4 Value of each variables (r=10 μm)
对比可知,r对σmax的影响也会出现“越小越强”的现象。当r为0.1 μm时,改变h,会出现脆-塑性去除的临界转变值。当r为10 μm时,塑性去除的阈值范围较宽。而r为1 μm时,所研究h范围几乎没有塑性去除的临界值出现。对比表3和表4最后一组数据可知,r增大也会强化磨削热的产生。磨削Ti6Al4V合金时,应尽量避免使用r≈1 μm的磨粒;当r≈0.1 μm时,增加h,有利于高质量的表面形成;选用r≈10 μm时,可参考文中h的数据,适当增加h可以提升磨削效率。对比图6和图7可知,r尺寸取 1~10 μm范围,磨粒刃圆半径对工件材料实现脆、塑性切削的影响比磨削深度的影响更大。
3 结论
1)基于应变梯度塑性理论的 J-C材料本构模型,建立了考虑单磨粒刃圆半径、磨削深度的切屑根部有效流动应力的热-力耦合有限元分析模型。用该模型验证了工件材料在微磨削时的尺度效应现象。
2)针对Ti6Al4V合金材料,当刃圆半径为0.1 μm时,适当调整磨削深度,磨削过程可能出现脆-塑临界转变,进入塑性去除阶段。当磨削深度为0.17 μm时,磨削热的热软化效应开始对切屑根部材料的有效流动应力产生主要影响。当刃圆半径为1 μm时,几乎不出现材料塑性流动的现象,磨削时应注意避免。当刃圆半径为10 μm时,磨削均处于条件模型中的塑性去除阶段,其塑性去除域的范围较宽,未出现临界磨削现象,可继续增加磨削深度以提高效率。
3)在微磨削下,磨粒刃圆半径与磨削深度对材料切屑的形成有重要影响,但并非尺寸越小越好。当r为1~10 μm时,磨粒刃圆半径对工件材料脆、塑性磨削的影响比磨削深度的影响更大。

