弯管液固两相流冲蚀失效模拟分析
曹学文,胥锟,彭文山
(中国石油大学(华东)储运与建筑工程学院,山东 青岛 266580)
冲刷腐蚀是金属表面与流体之间由于高速相对运动而引起的金属损坏现象,是一种危害性较大的局部腐蚀[1],存在于石油、航空、机械、建材、航天、能源、冶金等很多领域中[2—3]。冲蚀己经成为材料磨蚀破坏甚至设备失效的主要缘由之一[4—5],但目前对冲蚀的了解还不够全面,特别对多相流冲蚀的预防是难点。管道在运送介质时,暴露在运动流体中的管件都会受到不同程度冲蚀的破坏,尤其是弯管处的磨蚀速率比直管处要高出几十倍[6],破坏形式为沟槽、减薄,甚至断裂,该现象严重危害到油气田安全生产的要求。
国内外很多学者对液固两相流冲蚀进行了数值模拟研究,研究主要集中在流体参数变化对管件冲蚀的影响。Anthony等[7]用PHOENICS软件对U型管内两相流冲蚀进行数值模拟,得到湍流对固体粒子的影响规律;J Postlethwaite等人[8]提出了适用于管流液-固两相流的冲蚀模型,此模型计算得到的冲刷腐蚀率与实验结果能较好吻合;丁矿等人[9]使用CFD(计算流体力学)方法,得到了流速、颗粒浓度和颗粒直径对最大冲蚀率有明显影响的结论;王凯等人[10]研究了 Stokes 数对于冲蚀率的影响,分析了特定流量、一定粒径的颗粒在特定流速下的冲蚀;郑玉贵等[11]讨论了流体力学因素的重要性,论述了如何从流体力学方面控制冲刷腐蚀;郑友取等`考虑到壁面粗糙度与颗粒旋转等因素,对管内固体颗粒的冲蚀特性做了深入的研究,为管道的防磨提供了较为可靠的数值依据和理论参考。以上研究并没有考虑砂粒颗粒、不同重力方向等参数对弯管冲蚀的影响。文中建立数值模拟模型,利用 CFD方法探究流速、粒径、砂粒质量流量、操作压力、重力方向等对弯管冲蚀的影响,对于进一步研究多相混输管道冲刷腐蚀机理,进而保障油气田安全生产提供参考。
1 计算模型
1.1 离散相控制方程
流体中固体颗粒的受力方程式为:
式中:u为液相速度,m/s;dp为砂粒直径,m;up为砂粒速度,m/s;ρ为连续相气体密度,kg/m3;gy为y方向重力加速度,m/s2;μ为气体黏度,Pa·s;ρp为砂粒密度,kg/m3;Rep为相对 Reynolds数;Cd为drag系数;FD(u-up)为单位质量颗粒受到的阻力;Fy为y方向的其他作用力(包括虚拟质量力、压力梯度力和 Saffman升力);对于球形颗粒,在一定Reynolds数范围内,a1、a2和a3为常数[14]。
1.2 冲蚀模型
管道形状、流体参数、颗粒参数、冲击角度等都是影响冲蚀的因素。文中涉及的参数主要包括流速、砂粒质量流量、砂粒粒径、操作压力、重力方向。使用Huser等[13]提出的壁面碰撞模型进行冲蚀计算:
式中:Rerosion为壁面冲蚀速率,kg/(m2·s);C(dp)为颗粒直径的函数;N为碰撞颗粒数目;up为颗粒相对于壁面的速度;b(v)为相对速度的函数,取2.6;mp为砂粒质量流量,kg/s;θ为颗粒对壁面的碰撞角,(°);Aface为壁面计算单元的面积,m2;f(θ)为侵入角的函数,m/s。
2 数值模拟
CFD方法具有成本低、省时、高效、模拟真实等优点,已经成为又一种研究冲蚀问题的有效方法。该方法通过计算得出速度场、压力场等变量的具体分布,利用冲蚀方程完成冲蚀问题的预测和冲蚀量的计算。
2.1 管道参数
弯管模型如图1所示,弯管管径D=40 mm,弯径比R/D=1.5。常温条件下,以水作为连续相介质,入口速度为4 m/s,从上游水平直管L1=2000 mm入口流入,从下游竖直向下L2=800 mm直管流出。粒径为200 μm,离散相砂粒密度为2650 kg/m3,假设砂粒的初始速度与水相同,质量流速为0.1 kg/s。
2.2 网格划分与弯管长度设定
网格无关性分析即网格独立性分析,目的在于避免由于网格不同类型和大小的划分而引起模拟结果的误差。研究对象如图1所示,设置入口速度为4 m/s。采用非结构化网格,管壁处为加密的边界层网格。调整第一层网格大小为0.6 mm,网格渐变率为1.2,层数为5层,中心区域的网格大小为 2 mm。待考察的变量为弯管最大冲刷腐蚀速率,最大冲蚀速率与网格关系曲线如图2所示。可以看出,在较少网格数目下,腐蚀速率随着网格数目的增多呈现波浪形不规则变化,当网格数目达到9.8×105后,最大冲刷腐蚀速率趋于稳定。因此,在现有计算资源的前提下,为最大限度减少计算误差,在划分网格时选用网格数为 9.8×105的网格划分方法。
2.3 边界条件设置
随着CFD技术的发展及相关软件的开发,通过数值模拟方法获得流体内部的速度场、压力场等信息成为可能[15]。文中数值模拟设置如下:对于连续相的液态水,计算中速度进口边界条件定义为velocity inlet,出口边界条件定义为 pressure outflow,湍流强度为5%,利用k-ε湍流模型和壁面函数法,用标准壁面方程处理近壁面问题,直接将近壁面上的变量与湍流中心区内的变量用半经验公式联系起来,壁面采用无滑移边界条件,模拟过程使用分离算法求解,压力修正法采用易于收敛且不易波动的压力耦合方程组的SIMPLE算法,设置壁面条件为wall壁面;对于离散相的颗粒,DPM模型中进口和出口处采用逃逸(Escape)条件,壁面采用反弹(Reflect)条件,反弹系数公式见式(5)、(6)。
法向反弹系数:
切向反弹系数:
详细模拟设置参数见表1。
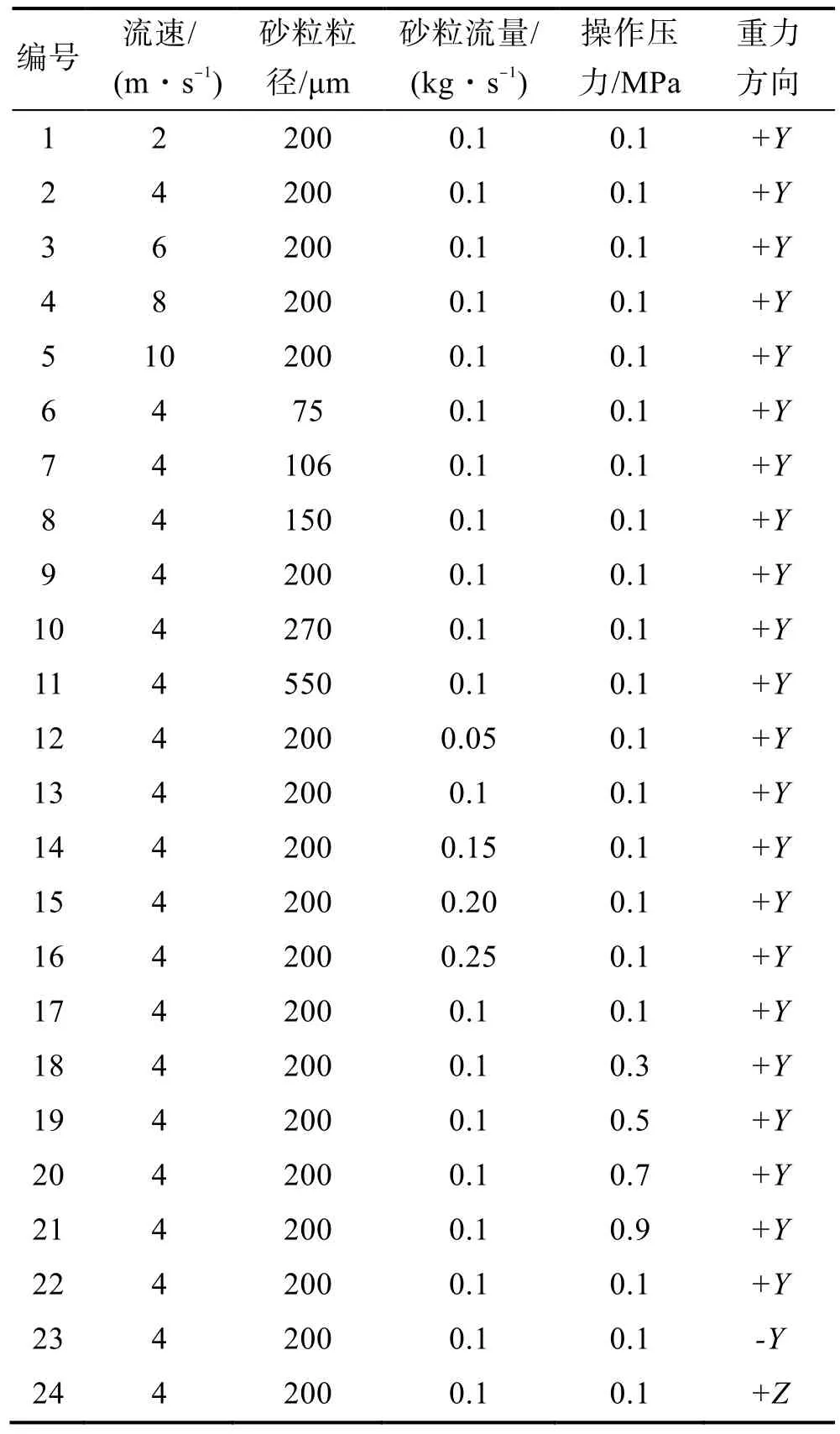
表1 数值模拟参数Table1 Numerical simulation parameters
3 弯管冲蚀模拟结果分析
3.1 不同流速下的冲蚀云图与砂粒轨迹图
由1—5组数据模拟可得不同流速与最大冲刷腐蚀的关系如图3所示。弯管冲蚀减薄分布与砂粒轨迹如图4所示。
由图3可知,当流速等于2 m/s时,低流速使得大量砂粒在管底流动,所以冲蚀部位主要集中在水平直管段底部。当流速增加到4 m/s后,管内湍动能增加,液固分层现象消失,冲蚀破坏部位由直管底部转向弯头两颊及外拱壁处。一方面随流速的增大,砂粒与管壁接触时的相对速度变大,砂粒的动能增加,砂粒对管件的碰撞冲蚀量增加;另一方面,速度的增大导致碰撞壁面的频率增高;两方面的共同作用导致冲蚀程度越来越严重。由图4可知,弯头处靠近内拱壁面冲蚀最轻微,外拱壁面冲蚀破坏现象最严重。这主要是由流体在流经弯头处受离心力作用所引起的,大量流体被甩向曲率半径较大的外拱壁面,加剧了外拱壁的冲蚀破坏程度。
3.2 不同砂粒粒径下的冲蚀云图与砂粒轨迹图
由 6—11组数据模拟可得不同粒径与最大冲刷腐蚀速率的关系如图5所示。弯管冲蚀减薄分布与砂粒轨迹如图6所示。
由图5可知,最大冲刷腐蚀速率随着颗粒直径的增加先减小,然后上升。主要原因是在粒子直径较小时,保持质量流量不变的情况下,粒子数量变多,粒子冲击壁面的频率较大,从而导致冲蚀速率较大;随着粒子直径的增大,保持质量流量不变的情况下,虽然砂粒数量逐渐减少,冲蚀破坏的范围与冲击壁面的频率减少,但是单个砂粒的能量增大,加剧弯管的冲蚀破坏,最终导致最大冲刷腐蚀速率增加。最大冲蚀速率先下降后上升的趋势是由颗粒数量和颗粒直径两者共同决定的。由图6可知,砂粒粒径越小,冲蚀破坏范围越分散;砂粒粒径越大,冲蚀破坏的范围越集中,粒径的变化不会引起最大冲刷腐蚀位置的改变。
3.3 不同砂粒流量下的冲蚀云图与砂粒轨迹图
由12—16组数据模拟可得不同砂粒流量与最大冲刷腐蚀速率的关系如图7所示,弯管冲蚀减薄分布与砂粒轨迹如图8所示。
由图7可知,随着砂粒流量的增加,提高了颗粒与壁面碰撞的几率,管件的最大冲蚀量显著增加。最大冲蚀量曲线整体呈上升趋势,这说明了管道含砂量的增加加强了对管道的冲刷冲蚀作用。由图8可知,砂粒质量流量增大,冲击壁面的粒子数量增多,冲蚀破坏范围扩大,单位面积壁面区域粒子冲击频率增加,导致冲蚀速率变大。固体颗粒含量增多,使得固体颗粒在弯头中运动时颗粒间的相互碰撞增大,所以最大冲蚀率的变化并不成明显直线上升趋势。另外,根据其冲蚀云图可知,冲蚀位置保持不变。
3.4 不同管内操作压力冲蚀云图与砂粒轨迹图
由 17—21组数据模拟可得管内不同操作压力与最大冲刷腐蚀速率的关系如图9所示,不同管内操作压力下弯管冲蚀减薄分布与砂粒轨迹如图10所示。
由图9可知,随着管内操作压力的增加,管道材料的最大冲蚀量呈微弱减小趋势。虽然最大冲蚀量曲线整体上呈下降趋势,但是与流速、颗粒直径、颗粒流量、不同重力方向等因素相比,管内操作压力的影响微弱,对管道的冲蚀作用影响较小。由图10可知,操作压力的变化对弯管冲蚀减薄分布影响较小,冲蚀破坏区域保持不变。
3.5 不同重力方向的冲蚀云图与砂粒轨迹图
由22—24组数据模拟可得不同重力方向与最大冲刷腐蚀速率的关系如图11所示,不同重力方向下弯管冲蚀减薄分布与砂粒轨迹如图12所示。
由图11可知,弯管的不同放置位置会影响冲蚀速率大小。弯管内介质流动方向为水平-垂直向下(图12a)时,最大冲蚀速率为 1.50×10-7kg/(m2· s);弯管内介质流动方向为水平-垂直向上(图12b)时,最大冲蚀速率为1.86×10-7kg/(m2·s);弯管水平放置,流体介质与重力方向垂直(图12c)时,最大冲蚀速率为1.66×10-7kg/(m2·s)。冲蚀破坏最小的是水平-垂直向下放置,此时弯头出口流向与重力方向一致;其次是弯管水平放置,此时弯头出口流向与重力垂直;最严重的是水平-垂直向上放置,此时弯头出口流向与重力方向相反。由此可知,弯头放置角度会影响弯管的冲蚀速率,该结论对弯管的现场施工有着极其重要的参考价值。由图12可知,最大冲蚀破坏总是出现在弯头出口处,而且不随出口方向的改变而改变。
4 结论
1)在一定范围内,弯管最大冲刷腐蚀速率随流速、砂粒流量的增加而增加。
2)随着砂粒直径的增加,弯管最大冲刷腐蚀速率呈先减小后增加趋势。
3)管内操作压力的增加对冲刷腐蚀速率的影响较小。
4)不同重力方向的弯管,冲蚀破坏最小的是出口直管竖直向下放置,其次是出口直管水平放置,最严重的是出口直管竖直向上放置。

