基于小波变换去噪预处理的EMD谐波检测方法

吕帅，张靠社（西安理工大学电力工程系，陕西西安　710048）

基于小波变换去噪预处理的EMD谐波检测方法

吕帅，张靠社
（西安理工大学电力工程系，陕西西安710048）

谐波检测；经验模态分解；模态混叠；小波变换

电力网络中之所以能够产生高次谐波，归因于非线性电子装置被大量使用。尤其近年来分布式电源被广泛应用，微电源的接入给电力系统的电能质量带来了严峻的挑战，特别是谐波污染问题急需治理［1］。还有，随着国家经济技术的不断发展，高铁、动车的开通路线越来越多；人们的环保意识不断增强，使用电池驱动的车辆数量也在急剧增加。而这些非线性负荷产生的谐波，要求电力系统的供电质量需要进一步提高［2-3］。

谐波的滋生会给电网带来诸多风险，使供配电系统的工作效率大大降低，而网损却大大升高；给大量用电装备带来额外损耗，减少使用时间。此外，可能会影响各级保护装置的正确动作，这样会使电网蒙受严重损失［1］。

至今，学者们一直还在研究谐波检测算法，提出了许多算法或者改进算法。如基于FFT检测方式、ip-iq法的电流检测［4］、小波变换检测法［5］以及基于LMS自适应原理检测法［6-7］等。其中，FFT检测法需要进行多次变换，计算过程复杂，计算耗时长，所以检测时间较长，误差也大；基于ip-iq理论检测法的优劣依赖低通滤波器的性能，现有的文献中，检测出基波电流有0.02 s多的延迟；尽管文献［3］所检测出基波电流具有很好的反应能力，但由于小波函数能量分散，易造成频谱混叠。并且小波变换必须建立基函数，基函数的选择决定信号分析结果，但是最优基的选取没有绝对的规律，所以基函数的选取很有难度。自适应谐波检测法尽管动作响应速度快，但这与滤波效果是相悖的，一般为了达到滤波效果，只能“牺牲”谐波提取的实时性。

经验模态分解法能够快速响应地将采集到的电力信号分解成各异尺度的特征模态函数，也就是IMF。因为EMD分解的完备特性，不同的IMF表示不同的特征分量，即可获得基波和高次谐波分量，从而完成电流中谐波的检测。因为电网结构层次多样且干扰信号多，实际中，采集到的信号，一般都会被噪声污染。谐波检测时，首先要保证尽可能地滤除噪声，并且要最大限度地留下谐波及基波信号。由于噪声的干扰会影响EMD分解谐波的质量［9］，对于噪声干扰这个问题，文章提出对信号先进行小波变换去噪，之后再进行EMD分解。经MATLAB仿真分析得出，该方法能够提高谐波检测的精度和适用性。

1　基于EMD的谐波检测方法

20世纪末，Norden E．Huang学者提出经验模态分解方法。该理论利用数据局部特征时间尺度，将数据中本身固有特征依次提取出来即（IMF），最后剩下一个残余分量，其中残余分量能够表现信号缓慢变化量。对分析不同IMF，能够更精准快速地掌握原信号的重要信息。

每阶IMF必须满足以下2个条件：1）分解得出的每一个IMF曲线，其零值点和极值点的总数相等或者二者差值不超过1；2）IMF均值为0。

设x（t）为连续信号，进行EMD分解。具体过程细节如图1所示。

第一步，求出x（t）曲线上的所有极点，随后，用样条插值法分别把极值点拟合成上包络emax和下包络emin。

如若h1（t）不满足EMD理论要求IMF须具备的2个条件，需要把h1（t）作为原始信号再次重复第一步：

这样筛选i次直到h1i（t）变为一个合格的IMF，即：

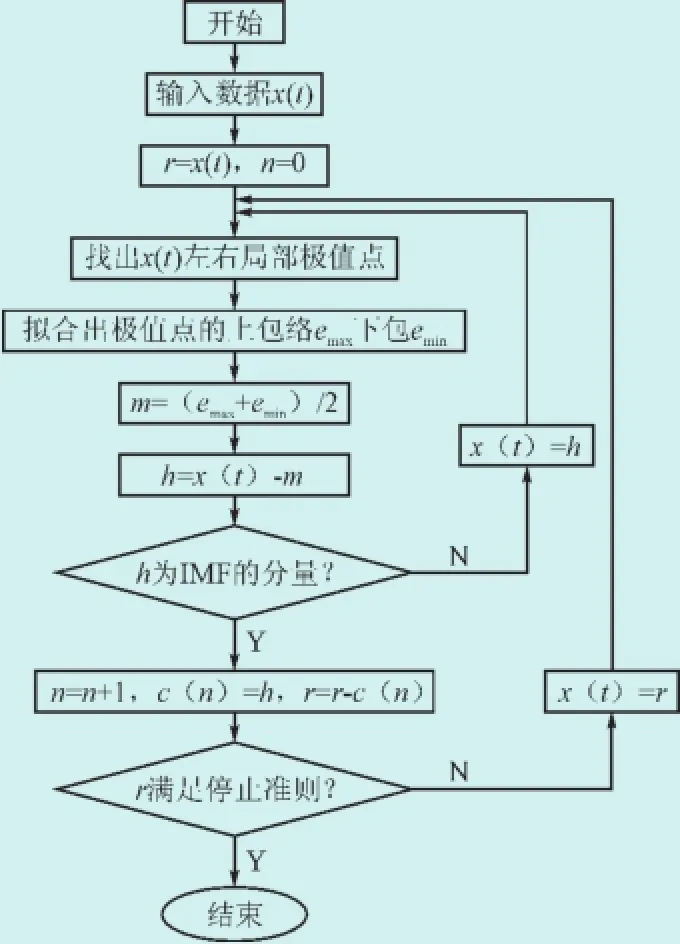
图1EMD分解流程图Fig.1　EMD decomposition flow chart

但在这个剩余信号r1（t）中仍有固有特征IMF分量，故要对r1（t）如此反复的筛选。这样依序会筛选出下一阶IMF和下一阶剩余信号，一直到最后一阶IMF和最后一阶残余量。这一过程可表示为：

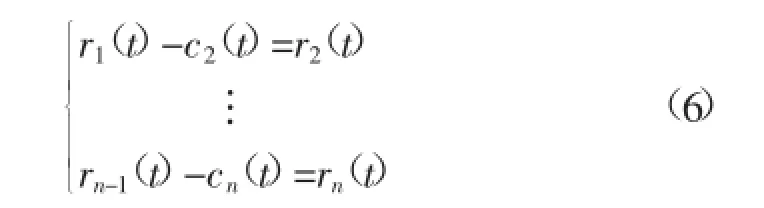
最后当rn（t）单调时，循环停止。从式（6）可得：

这样就把x（t）分解成为若干IMF和残余量之和。

EMD这种自适应时频信号分析方法，成功地被学者们应用到了各行各个领域，来解决疑难问题。但是EMD也有些自己的缺点，比如会产生虚假分量及模态混叠［8］，体现在两个方面：一是独立的IMF中包含全异尺度；二是同种尺度出现在多个IMF中。

假如不对原始信号端点进行延拓，直接分解信号，则包络线在端点处会出现上下交叉的偏差，导致求取的均值产生误差，使EMD分解得到的IMF在信号两端点周围失真。若截取信号较短，还会影响信号内部，这样会使得IMF失去意义。这就是EMD端点效应问题。

本文采取线性外推法对信号端点进行延拓，此方法比经镜像闭合延拓［9］、极值镜像延拓［10］以及遗传算法延拓算法［11］，更简单，实施方便，也能满足APF所要求的实时性检测能力。线性外推首先根据离端点最近的2个极大（小）值点，求出一条直线，延长此直线并和左（右）端点横坐标对应轴交于一点，然后对比左（右）侧端点与交点处的值的大小。选取极大值时，若交点值小于端点值，则端点处，选择端点近似为该处极大值点（图2），反之，选择交点近似为该点处极大值（图3）。极小值点类似。

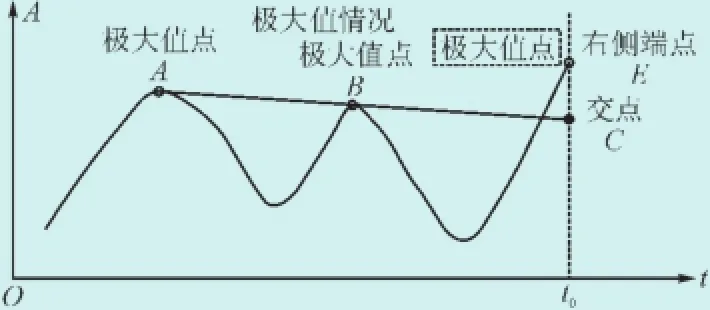
图2　端点是极大值情况Fig.2　The condition when the endpoint is at the maximum value

图3　交点是极大值情况Fig.3　The condition when the intersection is at the maximum value

2　算例分析

根据实际电网负载电流，设置负载电流信号。其中，采样频率20 000 Hz，在0～0.1区间采点数20 000个。表达式为：

I（t）=100sin（100πt）+50sin（300πt）+40sin（500πt）+30sin（700πt）（5）

式中：首项表示工频含量，幅值100 A，频率50 Hz。其余项从左向右是3、5、7次谐波，幅值依次为50 A、40 A、30 A，如图4所示。EMD分解信号，从图5和图6中看出，EMD能够完整分离工频含量（图5）以及在检测出信号中其余谐波分量（图6，频率单位10 Hz）。证明出该方法分解信号的可行性。

给信号加入SNR为25 dB的高斯白噪声后，从图7看出，仿真信号彻底“淹没”在噪声当中。直接对含噪声的电流信号进行EMD分解，如图8所示。

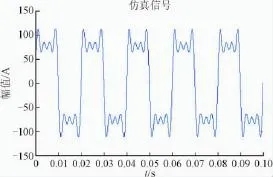
图4 仿真信号Fig.4　Simulation signal

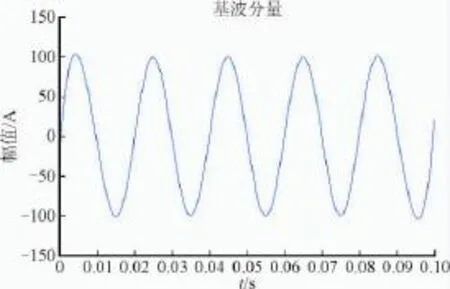
图5 基波分量Fig.5　Fundamental component

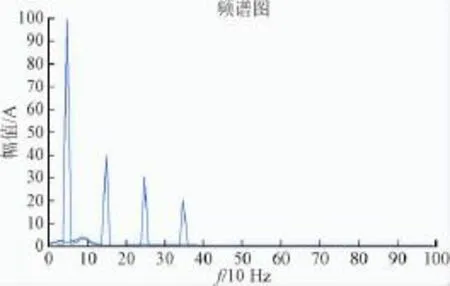
图6 信号能量频谱图Fig.6　Signal energy spectrum

图7　加入白噪声后的仿真信号Fig.7　Simulation signal after added white noise

由图8分解结果可知，EMD在含噪声的谐波电流中提取基波电流的效果不是很理想。因受到干扰，出现严重失真。基波电流没能有效的被提取出来，由此说明白噪声对EMD分解产生了不利的影响。

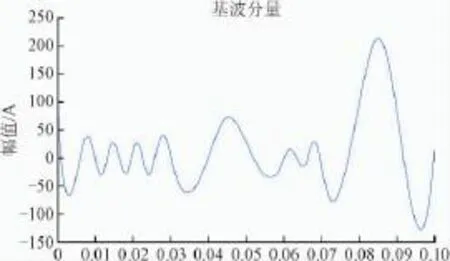
图8 EMD在含噪信号中分离基波结果Fig.8　The result of EMD separation of the fundamental wave in the noisy signal

故本文先对信号进行小波变换去噪。通过仿真分析知，信号去噪后，SNR是39.684 1 dB，去噪效果比较理想（图9）。再对降噪电流EMD分离，结果如图10。

图9　消除白噪声后的仿真信号Fig.9　Signal simulation after the white noise is eliminated

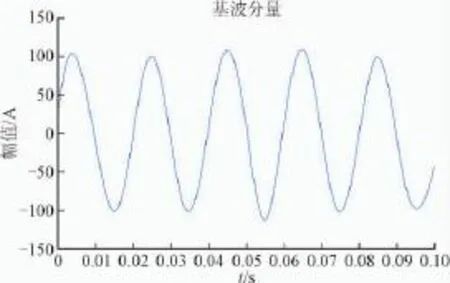
图10 基波分量Fig.10　Fundamental component

EMD分解去噪后仿真信号，从图10中看出，虽然经过预处理，但还是因为噪声对基波分离有一定的影响。不过根据图11的频谱分析，这样的预处理后，仍能够将谐波与基波有效的分离开来，能够实现有源滤波器的谐波检测功能，误差在允许的范围内。

3　结论

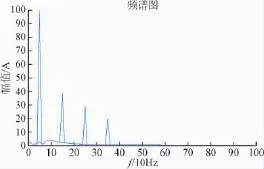
图11　信号能量频谱图Fig.11　Signal energy spectrum

通过EMD法分解，把含谐波的正弦信号分解成为包含各阶次谐波的IMF分量和工频分量，从而检测出电网中的谐波分量。对于算法的端点效应问题，文章采用线性外推改善其影响。提出采用小波变换法对含噪声的谐波电流源进行去噪预处理，再对处理后的谐波信号EMD分解。此方法能够有效降低噪声对EMD谐波检测的不利影响，使得各谐波分量能够从信号源中提取出来，提高了EMD谐波检测的精度与适用性。

［1］韩民晓，刘迅.分布式电源并网中电能质量相关规范探讨［J］.电力设备，2007，8（1）：57-60. HAN Minxiao，LIU Xun.Power quality standard consideration for the connection of distributed generation to main grid［J］.Electrical Equipment，2007，8（1）：57-60 （in Chinese）.

［2］雍静，娄方桥，王一平，等．低压配电系统单相非线性负荷的谐波衰减效应研究叨［J］．中国电机工程学报，2011，31（13）：55-61．YONG Jing，LOU Fangqiao，WANG Yiping，et al．Investigation on the harmonic attenuation effect of single-phase nonlinear loads in low voltage distribution system［J］．Proceedings of the CSEE，201l，31（13）：55-61（in Chinese）．

［3］王成山，武震，李鹏.微电网关键技术研究［J］.电工技术学报，2014，29（2）：1-9. WANG Chengshan，WU Zhen，LI Peng.Research on key technologies of microgrid［J］.Transactions of China Electrotechnical Society，2014，29（2）：1-9（in Chinese）.

［4］汪飞，毛华龙，许德志，等.多变电网条件下的对称序列与谐波检测［J］.电工技术学报，2014，29（12）：158-165. WANG Fei，MAO Hualong，XU Dezhi，et al.Symmetrical sequence and harmonic detection in varied grid conditions［J］.Transactions of China Electrotechnical Society，2014，29（12）：158-165（in Chinese）.

［5］吴勇，郭京蕾．小波变换在电网谐波电流检测中的应用［J］．武汉理工大学学报（信息与管理工程版），2007，29（7）：56-58．WU Yong，GUO Jinglei.Application of wavelet transform in harmonic detection of［J］.Journal of Wuhan University of Technology（Information and Management Engineering Edition），2007，29（7）：56-58（in Chinese）.

［6］付振宇，刘觉民，张彦林．瞬时检测谐波及无功电流的单相有源滤波器研究［J］．电气传动，2006，36（3）：29-31．FU Zhenyu，LIU Juemin，ZHANG Yanlin.Study on instantaneous detection of harmonics and reactive currents in single phase active power filter［J］.Electric Drive，2006，36（3）：29-31（in Chinese）.

［7］蒋平，邓俊雄，曹莹．一种先进的电网谐波检测方法［J］．电工技术学报，2000，15（6）：70-74．JIANG Ping，DENG Junxiong，CAO Ying.A method of harmonic detection of advanced［J］.Journal of Electric Technology，2000，15（6）：70-74（in Chinese）.

［8］石敏，吴正国，尹为民．基于RLS算法的时变谐波检测［J］．电工技术学报，2005，20（1）：50-53．SHI Min，WU Zhengguo，YIN Weimin.Based on RLS algorithm for time-varying harmonic detection［J］.Journal of Electric Technology，2005，20（1）：50-53（in Chinese）.

［9］FLANDRIN P，RILLING G，GONACALVES P．Empirical mode decomposition as a filter bank［J］．IEEE Signal Processing Letters，2004，11（2）：112-114．

［10］黄大吉，赵进平，苏纪兰.希尔伯特-黄变换的端点延拓［J］.海洋学报，2003，25（1）：1-11. HUANG Daji，ZHAO Jinping，SU Jilan.Endpoint hilbert huang transform extension［J］.Marine Journal，2003，25 （1）：1-11（in Chinese）.

［11］瞿伟廉，程磊.应用径向基函数神经网络处理EMD方法中的边界问题［J］.华中科技大学学报（城市科学版），2006，23（4）：1-4. QU Weilian，CHENG Lei.Application ofradial basis function neural network EMD method in the boundary of the city［J］.Journal of Huazhong University of Science and Technology（Science Edition），2006，23（4）：1-4（in Chinese）.

（编辑李沈）

EMD Harmonic Detection Method of Denoising Preprocessing Based on Wavelet Transform

LÜ Shuai，ZHANG Kaoshe
（Department of Electrical Engineering，Xi'an University of Technology，Xi'an 710048，Shaanxi，China）

In this paper，the empirical mode decomposition （EMD）is taken as a method of harmonic detection.Through EMD decomposition，the sinusoidal signal containing harmonics is decomposed into the IMF component and power frequency component containing harmonics of all orders to detect harmonics from the power grid.The study finds that the sampling noise in the signal has a greater impact on the EMD decomposition and proposes is an EMD harmonic detection method based on wavelet transform denoising preprocessing.This method firstly uses the wavelet transform to reduce the influence of the random white noise on the signal，then the signal containing a small amount of white noise is decomposed by EMD.The MATLAB simulation analysis suggests that the proposed method can effectively eliminate the influence of the random noise on the detection of harmonics and improve the accuracy and applicability of the EMD harmonic detection.

harmonic detection；empirical mode decomposition；mode mixing；wavelet transform摘要：将经验模式分解（empirical mode decomposition，EMD）作为电网谐波的检测方法。通过EMD法分解，把含谐波的正弦信号分解成为包含各阶次谐波的IMF分量和工频分量，从而检测出电网中的谐波分量。研究发现采样信号中的噪声会对EMD的分解产生较大影响，提出了一种基于小波变换去噪预处理的EMD谐波检测方法。此方法首先用小波变换减少随机白噪声对信号的影响，随后对含少量白噪声的信号进行EMD分解。经MATLAB仿真分析，所提方法可以有效地消除随机噪声对谐波检测的影响，提高了EMD谐波检测的精度与适用性。

1674-3814（2016）06-0058-04

TM935

A

2015-10-20。

吕帅（1989—），男，硕士研究生，主要研究方向为有源滤波器谐波检测及处理；

张靠社（1965—），男，博士，副教授，从事电力系统分析方面的研究与教学工作。

青海省光伏并网技术重点实验室项目（2014-ZY34A）。

ProjectSupportedbyKeyLaboratoryofGridConnected Photovoltaic Technology of Qinghai Province（2014-Z-Y34A）.