基于简化FCS-MPC的风电并网逆变器研究

孙国凯，都放（沈阳农业大学信息与电气工程学院，沈阳　110161）

基于简化FCS-MPC的风电并网逆变器研究

孙国凯，都放
（沈阳农业大学信息与电气工程学院，沈阳110161）

三相并网逆变器；有限集模型预测电流控制；目标函数；电压空间矢量

由于世界性能源的短缺，能源危机日益突出，如何充分利用和开发再生能源，已成为人们共同关注的问题。随着人们对电能和用电设备优化利用的需求不断增强，风能作为发展迅速、最具潜力的再生能源之一，已为人们的生活和发展做出了巨大的贡献。三相风力发电并网逆变器作为风力发电的关键设备，直接影响输出的电能质量，因而得到来自不同机构与学者的广泛研究。

对于三相风力发电并网逆变器，近年来学者们相继提出许多新颖、复杂的控制策略［1］。这些控制策略的共同目的是实现高功率因数、较快的动态响应以及输出电流正弦等［2］。通常的方法是采用比例积分（proportional integral，PI）控制策略［3］。该方法是通过对三角波进行比较，控制逆变器的输入电压，从而达到所期望的电流。该方法具有快速的动态响应，但在参考电流和输出电流之间存在一个稳态相位误差，造成电网侧电流畸变率上升，同时逆变器输出的开关频率不固定，造成滤波器的设计困难。为了解决上述问题，文献［4］提出了无差拍直接功率预测控制，该方法是建立在瞬时功率理论基础之上，利用脉宽调制模块在一个调制周期内，为了同时消除有功功率与无功功率的跟踪误差，从而能够获得开关频率固定的输出电压矢量与网侧的低次谐波电流。但该方法存在脉宽调制模块，使算法的实现变得相对困难。文献［5］提出了模型预测控制（model predictive control，MPC）技术，由于其能够充分考虑控制过程中系统约束条件与非线性特性，且具有快速的动态响应以及良好的稳态特性，易于实现，近年来被广泛研究与应用［5-7］。它将控制系统的被控参数（如变换器的输出电压、输出电流或开关频率等）以目标函数的形式表示，通过优化目标函数达到其控制目的。但是，MPC内在需要较高的采样频率，且采样频率越高，系统性能越好。而采样频率受到采样周期内计算量的限制，造成控制指令的时间延迟，影响系统性能。为了得到较好的控制行为，不同的简化模型预测控制算法相继被提出［8-11］：一种方法是间接离线法，它是将数据进行离线存储，之后利用查表法来实现，从而节省了在线计算时间。另一种方法是直接在线法，仅考虑变换器的有限开关状态，从而在预测过程中减少可能矢量的数量，然而，对于目前工业标准硬件来说仍然受到计算量的挑战。该问题对具有复杂拓扑结构的逆变器挑战性尤为突出。例如，在矩阵变换器和中点钳位变换器中，不同电压矢量的个数均为27。因此，在一个较短的采样周期中，传统的MPC算法很难完成上述计算量。

针对MPC算法存在的大量计算问题，提出了一种三相风力发电并网逆变器在线简化有限集模型预测控制（finite control set model predictive control，FCS-MPC）策略，该方法是将电压空间矢量技术与有限集模型预测控制算法相结合。首先利用电压空间矢量等效变换的原理，引入矢量扇区判断法，通过对候选扇区的矢量进行筛选，仅考虑其所在扇区相邻的3个电压矢量（2个有效电压矢量和1个零电压矢量）作为可能的有效电压矢量，在保持原有控制性能的基础上，避免了不必要的电压空间矢量的选择，从而使算法的执行时间大幅缩减，提高了算法的优化效率，进而实现了预测控制过程的在线简化。于此同时，通过预测下一时刻负载电流，利用目标函数对逆变器输出的不同电压矢量进行评估，选择使目标函数值最小的开关状态并在下一时刻作用于并网逆变器，而无需脉宽调制模块。最后，仿真结果表明，设计的模型预测控制器在运行过程中具有良好的控制性能，该算法能够准确地跟踪参考电流，解决了传统方法中存在的大量计算而影响控制性能问题，并在实际的应用中，有一定的借鉴作用。

1　三相并网逆变器数学模型

图1为本文所研究的带阻感负载两电平三相并网逆变器拓扑结构。设定ioa、iob、ioc为负载电流，voa、vob、voc为负载电压，Vdc为直流母线电压。文献［1］详细说明该并网逆变器的工作原理。

图1中，Ro为负载电阻；Lo为负载电感；eo为负载反电动势。

定义开关函数为：

功率管S1～S6与控制信号Sa、Sb、Sc之间的关系为：

根据开关状态（Sa，Sb，Sc）的不同组合，可以得到8种不同电压矢量［12］。

忽略三相交流输入线路负载的不对称性，可建立如式（3）所示的三相并网逆变器数学模型：

负载电压空间矢量vo表示为：

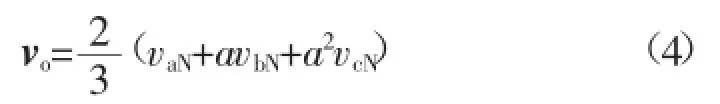
其中a=e-j2π/3，vaN、vbN、vcN分别是逆变器相电压。

负载电流空间矢量io表示为：

负载电动势空间矢量eo表示为：

负载电压空间矢量与开关状态的关系表示为：

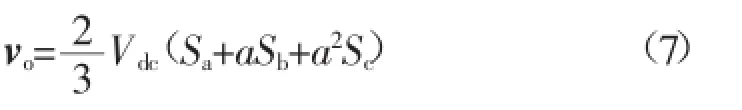
MPC是一种基于离散数学模型的优化控制算法，所以，为了FCS-MPC控制器的设计，需要将逆变器数学模型离散化。

其中k=NTs，N=0，1，2，3，…。

将式（8）代入式（3）得到如下表达式：

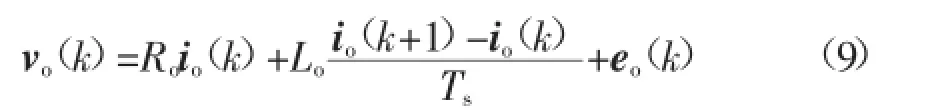
由式（9）可得，k+1时刻负载电流离散化模型为：

式中：io（k）为k时刻负载电流；io（k+1）为k+1时刻负载电流；vo（k）为k时刻的负载电压矢量。

式（10）构成了逆变器的输出电流预测模型，但该式中反电动势eo（k）未知并且很难测量，所以须对eo（k）进行估算。由式（10）可知，在第k个采样时刻，vo（k）、io（k）可以通过测量得到，io（k+1）为下一采样时刻的电流，所以，第k个采样时刻的反电动势可以由下式估算得到：

2　在线简化有限集模型预测电流控制策略

MPC优化问题可以简化和降低对系统行为的预测，只对可能的8种开关状态进行预测，通过目标函数的计算和比较，选择最优开关状态。预测的依据是在每个采样周期结束时使电流预测值与参考值之间保持误差最小，即目标函数最小原则。

2.1目标函数选择

式（10）作为MPC的控制器来预测每个开关状态下系统所有可能的输出电流值，由于共有8种可能的开关状态。将最接近参考电流值对应的一组开关状态并在下一时刻应用于并网逆变器，也就是说，选择使目标函数g最小的电压矢量：

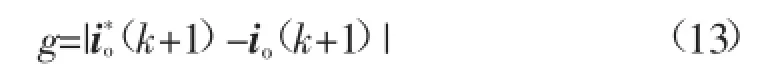
式（13）也可以表示为如下形式：

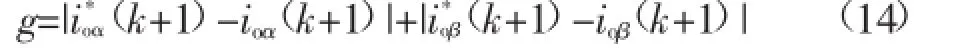
式中：ioα（k+1）和ioβ（k+1）分别为预测的k+1时刻负载电流在αβ坐标系下的分量，i*oα（k+1）和i*oβ（k+1）分别为k+1时刻参考电流在αβ坐标系下的分量。

2.2参考电流计算

根据MPC的基本原理，为使系统实际输出能够准确、快速地跟踪参考输出，系统k+1时刻的参考电流与预测电流误差要尽可能地趋近于0，其中预测电流由式（10）得到，而k+1时刻的参考电流由以下2种方法求解：

在采样时间足够小的情况下，可采取近似

当采样周期较大时，下一采样时刻参考电流值可以由如下拉格朗日外推公式预测得到：

仿真中采样周期设定为25 μs，所以选择式（16）所示参考电流计算方式更好。

2.3在线简化有限集模型预测控制

提出的模型预测电流控制框图如图2所示。通过预测系统下一采样时刻的参考电流值来预测参考电压，判断参考电压矢量所在扇区，仅考虑其所在扇区相邻的3个电压矢量（2个有效电压矢量和1个零电压矢量）作为可能的有效电压矢量。通过目标函数来计算参考值和预测值之间的误差。选择使目标函数g最小的开关状态并在下一时刻作用于并网逆变器。

FCS-MPC的实现需要寻找使目标函数最小的开关状态，并在下一时刻应用于逆变器。由此可以看出，由式（10）和式（13）得到，传统两电平并网逆变器FCS-MPC，通过计算8次预测电流和8次目标函数，才能选出最优电压矢量。

2.4控制流程

在线简化模型预测电流控制流程如下。首先对k时刻的电压、电流进行采样，包括三相负载电压和电流；由于参考电流来自外部控制环，当前时刻无法得知下一时刻的参考电流值I*o（k+1），因此需要对其进行预测；由参考电流计算参考电压，并判断参考电压所在扇区；选择参考电压所在扇区两侧的2个有效矢量和1个零矢量，作为3种可能的候选电压矢量，在每一种可能的有效开关状态下，由式（10）预测下一采样时刻的负载电流值io（k+1）；比较不同开关矢量的目标函数值，其中g（i）为第i个开关矢量所对应的目标函数值，选取最小目标函数对应的开关状态作为电路下一时刻的输入。

图2　模型预测电流控制框图Fig.2　Block diagram of MPC

2.5扇区判断

考虑到式（10），参考电压可以通过参考电流进行计算，用参考电流代替式（10）中的预测电流，可得到逆变器输出的参考电压矢量：

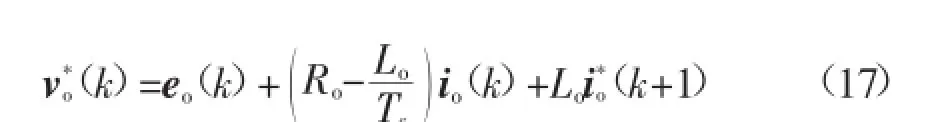
FCS-MPC采用离散时间模型在一个时刻内预测下一时刻状态，然后根据预先选择的目标函数选择最适当的控制行为。但由于传统的MPC算法存在计算量大的问题，提出一种减少计算量的在线简化FCS-MPC算法，相比于传统MPC算法考虑所有可能的电压矢量，所提出的FCS-MPC算法仅需要考虑所有可能电压矢量的一个子集，即判断参考电压矢量所在扇区，就可以获得所需的有效电压矢量。如表1所示。

三电压矢量选择法，这种电压矢量选择模式要求在每个开关周期内选择与参考电压矢量所在扇区相邻的两个有效矢量和一个零矢量。为了达到上述目的，参考电压矢量在不同扇区上的选择方法如表1所示。

三相并网逆变系统有三组桥臂，上面已给出电压空间矢量的8种工作状态。由于v0和v7表示零矢量，因此，如图4所示功率变换器在静止αβ坐标系下可分为6个扇区。理论证明［13］，当v落入某一扇区后，仅判断扇区2个边界有效矢量和一个零矢量，代入式（10）和式（13），选择使目标函数最小的电压矢量对应的开关状态，在下一时刻作用于并网逆变器。举例说明，当参考电压矢量落入第一扇区，选择该扇区邻近的两个有效电压矢量与一个零电压矢量，即第一扇区子集｛v0，v1，v2｝。通过目标函数选择一个该子集中的最优电压矢量对应的开关状态，并在下一时刻应用于并网变换器。

表1 电压矢量子集Tab.1　Subset of voltage vector

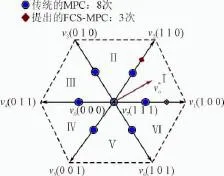
图3　电压空间矢量选择图Fig.3　Voltage vectors generated by the inverter

定义3个变量：

再定义3个变量A、B、C，通过分析可以得出：

若vref1＞0，则A=1，否则A=0；

若vref2＞0，则B=1，否则B=0；

若vref3＞0，则C=1，否则C=0。

令N=4×C+2×B+A，则可以得到N与扇区的关系：

位于第Ⅱ扇区；

当N=6时,位于第Ⅴ扇区；

3　仿真结果

为验证上述预测控制算法的有效性，本文用Matlab/Simulink搭建了三相并网逆变器FCS-MPC的系统模型，该模型及控制器的参数见表2。同时，本文对两电平三相带阻感负载并网逆变器进行控制，在稳态和暂态条件下，对所提简化有限控制集模型预测方法的性能进行评估，从逆变器输出电流谐波畸变率（THD）对比检验两者的控制效果。仿真及分析结果如图4—图8所示。

表2 控制器参数表Tab.2　Simulation parameters of system controller

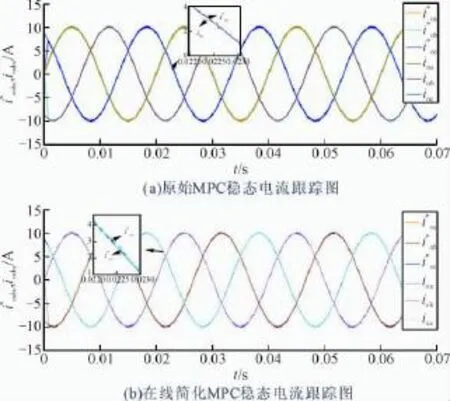
图4　三相电流稳态跟踪图Fig.4　Three-phase current diagram

在采样时间Ts=25 μs时，稳态和暂态情况下考虑不同情况的模型预测控制系统仿真结果如下。

3.1稳态分析

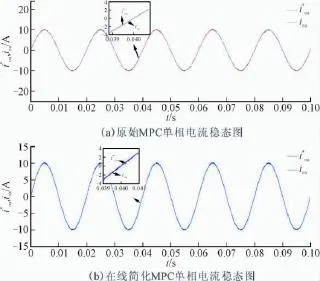
图5　单相电流稳态图Fig.5　Single-phase current for MPC

图6　电流阶跃变化图Fig.6　Reference current for a step

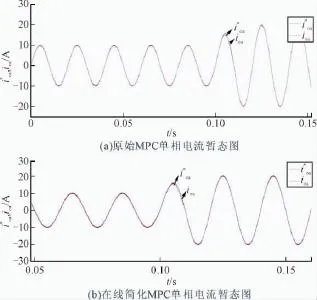
图7 单相电流阶跃变化图Fig.7　Single-phase current for a step

图8　参考电流i*α，i*β和负载电流iα，iβFig.8　Reference current i*α，i*βand load current iα，iβ

图4（a）（b）分别是参考电流幅值为10 A时，三相并网逆变器原始和简化后的MPC电流控制的稳态实验波形，图5（a）（b）分别是原始和简化后的MPC电流控制单相电流稳态实验波形，从图中可以看出三相并网逆变器电流的正弦度较好，能够很好地跟踪参考电流的变化，证明了简化的MPC在三相并网逆变器应用场合的可行性。原始和简化后的MPC系统畸变率（total harmonic distortion，THD）：原始THD= 1.23%，简化后的THD=1.22%。由图4—图5可以看到，负载电流的良好动态响应，上升时间快，无超调，电流谐波畸变率低。

3.2暂态分析

为说明该算法的有效性，将简化模型预测电流控制与传统的模型预测电流控制法进行对比分析。在t=0.1 s，参考电流值由10 A上升至20 A，而后保持不变。

图6（a）（b）是原始MPC和简化MPC三相参考电流在0.1 s时从10 A阶跃变化至20 A时的电流动态波形，图7（a）（b）分别是原始MPC和简化MPC单相参考电流在0.1 s时从10 A阶跃变化至20 A时的电流动态波形，从图中可以看出电流能够快速跟踪参考电流的变化，具有很好的动态性能，且两者均具有良好的电流跟踪效果。由此可以看出，在FCS-MPC计算负荷可以很大程度减少的情况下，控制性能没有受到影响。在FCS-MPC系统中，α和β相电流可以实现互相解耦，如图8所示。

4　结论

本文以三相并网逆变器为研究对象，搭建了三相带阻感负载并网逆变器的仿真模型，采用FCSMPC算法，针对该算法存在的大量计算问题，提出了一种三相并网逆变器在线简化模型预测电流控制策略。该策略对负载电流值进行预测，以电流误差最小为原则设计目标函数，通过预测参考电压矢量来减少可能的有效开关状态。仿真结果表明，所设计的模型预测控制器在三相并网逆变器带阻感负载运行过程中具有良好的静、动态控制性能，同时，该算法能够准确地跟踪参考电流，解决了传统方法中存在的大量计算的问题，在实际应用中，具有一定的借鉴作用。

［1］YARAMASU V，WU B，SEN P C，et al.High-power windenergyconversionsystemsstate-of-the-artand emerging technologies［J］.Proceedings of the IEEE，2015，103（5）：740-788.

［2］YARAMASU V，RIVERA M，WU B，et al.Model predictive current control of two-level four-leg inverters—part I：concept，algorithm，and simulation analysis［J］.IEEE Transactions Power Electronics，2013，28（7）：153-159.

［3］SAMIR K，PATRICIO C，RENÉ V，et al.Model predictive control-a simple and powerful method to control power converters［J］.IEEE Transactions on Industrial Electronics，2009，56（6）：1826-1838.

［4］BOUAFIA A，GAUBERT J P，KRIM F.Predictive direct power control of three-phase pulsewidth modulation（PWM）rectifier using space-vector modulation（SVM）［J］.IEEE Transactions on Power Electronics，2010，25（1）：228-236.

［5］JOSEÉ R，JORGE P，CÉSAR A，et al.Predictive current control of a voltage source inverter［J］.IEEE Transactions on Industrial Electronics，2007，54（1）：495-503.

［6］RODRIGUEZ J，KAZMIERKOWSKI M P，ESPINOZA J R，et al.State of the art of finite control set model predictive control in power electronics［J］.IEEE Transactions on Industrial Informatics，2013，9（2）：1003-1016.

［7］CORTES P，WILSON A，KOURO S，et al.Model predictive control of multilevel cascaded H-bridge inverters［J］. IEEE Transactions on Industrial Electronics，2010，57 （8）：2691-2699.

［8］BECCUTI A G，MARIETHOZ S，CLIQUENNOIS S，et al.Explicit model predictive control of dc dc switchedmode power supplies with extended Kalman filtering［J］. IEEE Transactions on Industrial Electronics，2009，56（6）：1864-1874.

［9］沈坤，章兢，王坚.一种多步预测的变流器有限控制集模型预测控制算法［J］.中国电机工程学报，2012，32 （33）：37-44. SHEN Kun，ZHANG Jing，WANG Jian.A model predictive control scheme of multi-step prediction finite control set for converters［J］.Proceedings of the CSEE，2012，32 （33）：37-44.

［10］AGUILERA R P，LEZANA P，QUEVEDO D E.Finitecontrol-set model predictive control with improved steadystateperformance［J］.IEEETransactionsonIndustrial Informatics，2013，9（2）：658-667.

［11］王宝诚，郭小强，梅强，等.三相并网逆变器脱网运行电压控制技术［J］.电网技术，2011，35（7）：91-95. WANG Baocheng，GUO Xiaoqiang，MEI Qiang，et al. Intentional islanding voltage control for three-phase gridconnected inverters［J］.Power System Technology，2011，35（7）：91-95（in Chinese）.

［12］杨勇，赵方平，阮毅，等.三相并网逆变器模型电流预测控制技术［J］.电工技术学报，2011，26（6）：153-159. YANG Yong，ZHAO Fangping，RUAN Yi，et al.Model current pedictive control for three-phase grid-connected inverters［J］.Transaction of China Electrotechnical Society，2011，26（6）：153-159（in Chinese）.

［13］ZHANG Y L，LIN H.Simplified model predictive current control method of voltage-source inverter［C］//International Conference on Power Electronics-ICPE，Jeju，2011：1726-1733.

［14］邓向阳，晁勤，袁铁江，等.三相联网逆变器电流控制策略研究［J］.电网与清洁能源，2011（5）：31-35. DENG Xiangyang，CHAO Qin，YUAN Tiejiang，et al. Current control strategies for three-phase grid-connected inverters［J］.Power System and Clean Energy，2011（5）：31-35（in Chinese）.

［15］李冬辉，桑元.一种基于SVPWM并网逆变器电流控制的研究［J］.节能技术，2014（5）：419-422. LI Donghui，SANG Yuan.The research of grid-connected inverter current control based on SVPWM［J］.Energy Conservation Technology，2014（5）：419-422（in Chinese）.

（编辑徐花荣）

Study of Wind Power Grid-Connected Inverters Based on Simplified FCS-MPC

SUN Guokai，DU Fang
（School of Information and Electrical Engineering，Shenyang Agricultural University，Shenyang 110161，Liaoning，China）

Model predictive control is widely applied in the three-phase grid-connected inverters.However，there is a large amount of calculation defects in the process of control，leading to the time delay of the control command，and hindering the application of the model predictive control.In order to solve the problem，a simplified finite control set model predictive current control method is proposed in this paper.The proposed method is achieved based on the stationary reference frame.The optimal voltage vector which minimizes a cost function is selected by using an iterative control algorithm without pulse width modulator.Meanwhile，to reduce the calculation defects，a sector distribution method is presented by using space vector modulation.Based on the three-phase grid-connected inverters with a resistive-inductive load，a system simulation model is established.The steady and transient performance of output currents are analyzed.Simulation results are presented to demonstrate the efficacy of the proposed method.

three-phase grid-connected inverter；finite control set model predictive control；objective function；voltage space vector摘要：三相风力发电并网逆变器的模型预测控制存在大量计算问题，导致控制指令的时间延迟，影响控制系统性能，严重阻碍系统应用。为克服上述难点，提出了一种在线简化有限控制集模型预测电流控制算法。该方法通过坐标变换构建αβ坐标下逆变器输出电流的预测模型，利用目标函数对逆变器输出的不同电压矢量进行评估，而无需使用脉宽调制模块。同时，结合电压空间矢量等效变换的原理，引入矢量扇区判断法，进而实现了预测控制过程的在线简化。最后，以带阻感负载三相并网逆变器为控制对象，建立了有限控制集模型预测控制仿真模型，分析了输出电流的稳态与动态性能。仿真结果验证了所提方法的有效性。

1674-3814（2016）06-0136-07

TM464

A

2015-12-14。

孙国凯（1963—），男，教授，从事地方电力系统及其自动化研究；

都放（1990—），女，硕士研究生，从事地方电力系统及其自动化研究。

国家科技部科技支撑计划（2012BAJ26B01-03）。

Project Supported by National Key Technology R&D Program of the Ministry of Science and Technology（2012BAJ26B01-03）.