基于贝叶斯方法的比例数据分位数推断及其应用
赵为华, 张日权
(1.南通大学 理学院,江苏 南通 226019; 2.华东师范大学 统计学院,上海 200241)
基于贝叶斯方法的比例数据分位数推断及其应用
赵为华1, 张日权2
(1.南通大学 理学院,江苏 南通 226019; 2.华东师范大学 统计学院,上海 200241)
为了尝试使用贝叶斯方法研究比例数据的分位数回归统计推断问题,首先基于Tobit模型给出了分位数回归建模方法,然后通过选取合适的先验分布得到了贝叶斯层次模型,进而给出了各参数的后验分布并用于Gibbs抽样。数值模拟分析验证了所提出的贝叶斯推断方法对于比例数据分析的有效性。最后,将贝叶斯方法应用于美国加州海洛因吸毒数据,在不同的分位数水平下揭示了吸毒频率的影响因素。
比例数据;分位数回归;Tobit模型;贝叶斯分析;Gibbs抽样
一、引 言
比例数据在很多实际问题中大量存在,如家庭食物消费支出占家庭收入的比例,某种疾病的临床治愈率,公司某项产品的市场占有率,银行到期贷款的按期偿还比例等。对比例数据的回归建模方法已有一些研究,如Peter和Tan基于单纯形分布研究了连续比例数据的回归参数估计问题[1];Ferrari等通过参数变换的方法,利用Beta 回归模型并借鉴广义线性模型的理论和方法研究了比例数据的估计及其诊断分析问题[2];Papke和Wooldridge提出了基于拟似然方法研究比例数据的回归建模问题[3];其他的一些相关工作详见Kieschnick、Zhao、Ramalho等人的研究成果[4-8]。
上述研究都是基于均值回归分析方法展开的,然而均值回归只能提供在平均意义下比例因变量与自变量之间的相关关系且易受异方差或异常值影响。在实例分析中,应用者希望全方位、多角度分析和揭示因变量与自变量之间的关系,分位数回归就能提供关于因变量的条件分布在不同分位点下的全面描述,进而能够得到在低、中、高等分位数下自变量影响因变量的动态变化关系。分位数回归最早是由Koenker等于1978年在研究计量经济建模时提出的统计方法, 与基于均值回归相比,分位数回归不受数据中异常点的影响,是一种稳健的估计方法,特别当分位数τ=0.5时即为中位数回归(俗称最小一乘方法)[9]。此外,分位数回归不需要Gauss-Markov条件假定,既能适应误差方差无穷的情形,又能方便地处理异方差、多峰数据等情形。关于分位数回归的详细内容可参见Koenker等人的专著[10]。
目前关于比例数据的分位数回归建模及其统计推断研究刚刚开始,主要原因是其估计的相关理论性质难以建立,以及如何将得到的大样本理论性质应用到实际数据分析中。相比于经典的频率方法,贝叶斯方法具有如下优点:贝叶斯方法原理简单且易实施;通过选取合适的参数先验,基于后验分布除了可以得到Bayesian后验估计值,同时可以得到Bayesian可信区间,这为我们提供一种选择相关重要自变量的方法;很多时候,特别在小样本时,由贝叶斯方法得到的结果要比基于频率方法得到的结果更可靠。为此,本文拟应用贝叶斯方法研究比例数据的分位数推断问题。
二、 比例数据的分位数回归建模
由于比例数据的有界性即取值在[0,1]上,因此直接基于Koenker的分位数回归建模方法会失效,得到的预测估计往往会超出上、下界。下面基于Tobit模型引进比例数据的分位数回归建模方法[10-12]。Tobit模型最早用来刻画因变量取值有上限或者下限时或者有极限值时提出来的,已在许多领域特别是计量经济学领域中有着广泛应用。经典的Tobit线性回归模型假定因变量取值有下界,并通过引入一个不可观测的潜在变量后模型可表示为:
y*=xTβ+ε
y=max(y0,y*)
(1)
其中y是一个观测因变量,y0是观测因变量的取值下限,y*是潜在因变量,ε是误差项,x=(x1,x2,…,xp)T∈Rp是p维自变量,β=(β1,β2,…,βp)T是回归系数。如果假定协变量中的第一个分量x1≡1,则模型(1)中包含了常数项。Tobit回归本质上是一种具有固定删失点的模型,国内外许多文献在均值回归和分位数回归下分别对Tobit线性回归模型展开过系统研究,建立了相关的大样本理论性质,并将研究结果应用于相关计量经济学问题。近年来,由于统计软件的计算能力快速提高以及贝叶斯方法的优点,一些文献基于贝叶斯方法研究了Tobit参数回归模型[13],Kaifeng Zhao等进一步研究了Tobit半参数回归模型贝叶斯推断方法[14]。
由于比例数据既有下界0又有上界1,基于模型(1)我们提出如下的Tobit模型:
y*=xTβ+ε
y=y*·I(0 (2) (3) 其中ρτ(u)=u(τ-I(u<0))是分位数损失函数,0<τ<1是分位数水平。尽管Tobit模型为比例数据的分位数回归建模提供了一条非常可行的途径,它可以处理连续型比例数据(因变量取值在开区间(0,1)时情形),半连续型比例数据(因变量取值在闭区间[0,1]或半开半闭区间[0,1)或(0,1]时情形),然而,直接基于式(3)不仅讨论系数估计的大样本理论性质是困难的,而且如何提出有效、快速的计算方法也是充满挑战的。由于贝叶斯统计的优点,下面我们基于贝叶斯方法提出比例数据的分位数层次模型,并基于层次模型提出各参数的Gibbs抽样方法。 (4) 其中0<τ<1称为偏度参数。进一步,式(4)可以等价地表示成如下的混合密度函数: (5) (6) i=1,2,…,n βj|sj,λ,σ~N(0,sj),sj|λ,σ~exp((λ/σ)2/2), j=1,2,…,p (7) 根据层次模型(6)以及式(7),我们可以得到如下各参数的后验分布: 2.β|y*,μ,λ,σ,e,s~N(η,Σ),其中Σ=(G+XTHX)-1,η=ΣHXTy*,G=diag(1/s1,1/s2,…,1/sn),s=(s1,s2,…,sp)T,H=diag(1/k2σ e1, 1/k2σ e2,…,1/k2σ en),X=(x1,x2,…,xn)T,xi=(xi1,xi2,…,xip)T。 根据各参数的后验分布,应用Gibbs抽样方法即可得到各参数的贝叶斯后验估计,如后验均值、后验中位数、后验标准差以及贝叶斯可信区间估计等。在Gibbs抽样中,我们每次模拟抽样15 000次,然后,为消除初值的影响剔除前面5 000次的抽样。下面的模拟分析和实例应用充分说明了本文给出的贝叶斯推断的有效性。 模拟数据由以下Tobit模型生成,y*=β0+β1x1+β2x2+β3x3+β4x4+0.5·ε,y=y*·I(0 从表1可以看出,在正态误差下和厚尾T分布下,系数的估计值都非常接近于真值,而且对应的区间估计随着样本量的增加,区间的长度在不断地变小。同时,我们注意到对于两个不相干变量x3和x4的系数估计,其95%的可信区间始终包含0。 不难看出,本文给出的Gibbs抽样方法是令人满意的,而且对厚尾误差分布,估计的结果也是非常稳健的。 此外,为了诊断Gibbs抽样的收敛性是否依赖于一些超参数的选择,在标准正态误差下,样本量n=300时,超参数a1=b1=0.1和a1=b1=0.5情形下回归参数的MCMC轨迹图*有需要了解的读者请与作者联系。。在轨迹图中我们发现其后验分布在不同初值下迅速地达到平稳分布,验证了本文所给的Gibbs抽样方法具有很好的收敛性且不依赖于初始参数的选择。 本文将比例数据的贝叶斯分位数方法应用到一个社会学问题中。数据来自于美国加利福尼亚州的一个防范公民毒品瘾君子研究机构(CivilAddictProgram),该研究主要为吸食了海洛因毒品上瘾后有刑事犯罪记录的瘾君子进行强制药物治疗,然后评价强制药物治疗是否对瘾君子之后控制吸食海洛因的使用频率以及其他一些问题产生积极影响。该项目持续跟踪调查研究了15年,总共有437个有效样本。以y表示最后一年中每月平均使用海洛因的频率(每月使用海洛因的天数/30天),解释变量主要包括跟踪的15年间吸毒人员每年进行药物治疗的平均月数(x1),15年间每年被监禁的平均月数(x2),首次接受治疗时的年龄(x3)和首次吸毒时的年龄(x4)。因变量中大约有40.5%取值为0,有24.9%取值为1,数据分布具有明显的不对称性和非常大的概率在区间端点取值,因此本文建议的比例数据回归模型非常适合此数据。考虑到有些解释变量取值的稀疏性并尽量消除解释变量取值的量纲影响,我们将x3和x4取值变换到单位区间上,将x1和x2变为取值离散化成0~1变量(按取值是否大于6进行划分)。在不同的分位数水平下,系数的估计及其95%可信区间估计拟合结果见表2。 表1 不同分位数水平下回归系数的点估计及其可信区间估计 表2 海洛因吸毒数据的参数估计和95%可信区间估计 本文提出了基于贝叶斯方法研究比例数据分位数回归建模及其统计推断方法。首先借鉴Tobit模型建立了比例数据分位数回归的贝叶斯层次模型,通过选取先验分布提出了Gibbs抽样程序。本文提出的方法既可以处理连续型比例数据,又可以处理半连续型比例数据。从模拟研究和实例分析可以看出,我们的估计方法是相当不错的,并且能动态地捕捉因变量与解释变量之间的动态关系,为问题分析提供更丰富的分析结果。在此研究基础上,今后进一步的研究方向是当比例因变量与解释变量之间存在非线性关系时,我们需要研究比例数据分位数回归非参数、半参数建模方法,并研究如何提出有效、快速的估计算法。 香港中文大学XinyuanSong教授和美国加州大学洛杉矶分校Yih-IngHser教授提供了海洛因吸毒数据,在此特表谢意。 [1]PeterS,TanM.MarginalModelsforLongitudinalContinuousProportionalData[J].Biometrics,2000(56). [2]FerrariS,Cribari-NetoF.BetaRegressionforModellingRatesandProportions[J].JournalofAppliedStatistics, 2004(7) . [3]PapkeL,WooldridgeJ.EconometricMethodsforFractionalResponseVariableswithanApplicationto401(k)PlanParticipationRates[J].JournalofAppliedEconometrics, 1996,11(6). [4]KieschnickR,McCulloughB.RegressionAnalysisofVariatesObservedon(0,1):Percentages,ProportionsandFractions[J].StatisticalModelling, 2003(3). [5]ZhaoW,ZhangR,LvY,LiuJ.VariableSelectionforVaryingDispersionBetaRegressionModel[J].JournalofAppliedStatistics,2014,41(1). [6]RamalhoE,RamalhoJ,MurteiraJ.AlternativeEstimatingandTestingEmpiricalStrategiesforFractionalRegressionModel[J].JournalEconometricsSurvery,2011,25(1). [7]李泽安,葛建芳,章亚娟.Beta回归模型在数据挖掘预测中的应用[J].南通大学学报:自然科学版,2009,8(3). [8]赵为华,张日权.Beta-Binomial回归模型及其应用[J].统计与信息论坛,2016,31(3). [9]Koenker,RogerBassett,Gilbert.RegressionQuantiles[J].Econometrica:JournaloftheEconometricSociety,1978(1). [10]Koenker,Roger.QuantileRegression[M].Cambridge:CambridgeUniversityPress,2005. [11]TobinJ.EstimationofRelationshipsforLimitedDependentVariables[J].Econometrica,1958,26(1). [12]AmemiyaT.TobitModels:ASurvey[J].JournalofEconometics,1984,24(1). [13]RahimAlhamzawi,KemingYu.BayesianTobitQuantileRegressionUsingG-priorDistributionwithRidgeParameter[J].JournalofStatisticalComputationandSimulation,2015,85(14). [14]KaifengZhao,HengLian.BayesianTobitQuantileRegressionwithSingle-indexModels[J].JournalofStatisticalComputationandSimulation, 2015,85(6). [15]AndrewsD,MallowsC.ScaleMixturesofNormalDistributions[J].JournaloftheRoyalStatisticalSociety,1974,36(1). BayesianInferenceforQuantileRegressionofProportionalDataandItsApplication ZHAOWei-hua1,ZHANGRi-quan2 (1.SchoolofScience,NantongUniversity,Nantong226019,China;2.SchoolofStatistics,EastChinaNormalUniversity,Shanghai200241,China) Inthispaper,wetrytouseBayesianmethodtoinvestigatetheregressionmodelingoftheproportionaldataintheframeworkofquantileregression.WefirstgivetheproposedquantileregressionforproportionaldatabasedonTobitmodel,andthenobtaintheBayesianhierarchicalmodelthroughchoosingappropriatepriordistributions,whichleadtotheposteriordistributionforGibbssamplingmethod.Theusefulnessandgoodperformanceofourproposedmethodisexaminedbythesimulationstudies.Finally,weapplynewlyproposedmethodtotheheroinusedatainCalifornia,andrevealtheinfluencefactorsofdrugusefrequencyatdifferentquantilelevels. proportionaldata;quantileregression;Tobitmodel;Bayesiananalysis;Gibbssampling 2016-02-28 教育部人文社会科学青年基金项目《比例数据的分位数回归建模》(14YJC910007);国家自然科学基金项目《函数型含指标项半参数回归模型的统计分析》(11571112) 赵为华,男,江苏海门人,统计学博士,副教授,硕士生导师,研究方向:回归建模及其应用; C812∶O212 A 1007-3116(2016)08-0009-05 (责任编辑:李勤) 张日权,男,山西大同人,统计学博士,教授,博士生导师,研究方向:分位数回归和半参数模型。 【统计理论与方法】三、 贝叶斯层次模型和Gibbs抽样
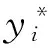

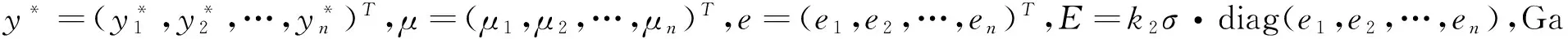
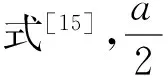
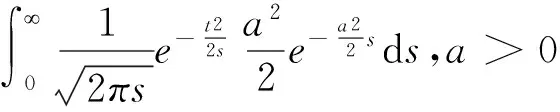
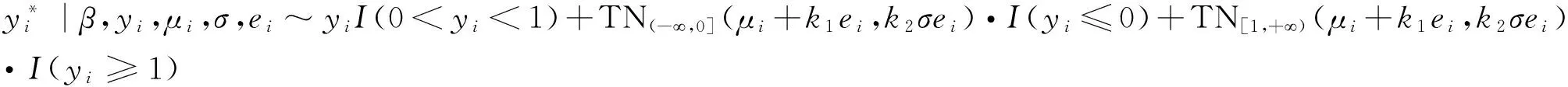
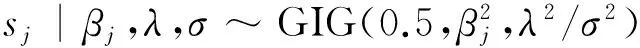

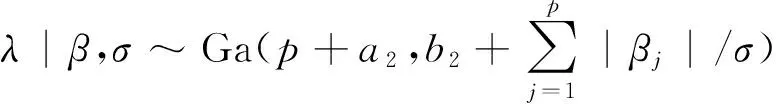

四、模拟研究
五、实例应用



六、总 结
——与非适应性回归分析的比较

