突发事件对国际石油期货价格波动的时间记忆性分析——基于PPM模型和Hurst指数分析
张跃胜
(1. 新乡学院 管理学院,河南 新乡453003;2. 西安交通大学 经济与金融学院,陕西 西安 710061)
突发事件对国际石油期货价格波动的时间记忆性分析
——基于PPM模型和Hurst指数分析
张跃胜1,2
(1. 新乡学院 管理学院,河南 新乡453003;2. 西安交通大学 经济与金融学院,陕西 西安 710061)
以国际原油期货价格波动日度数据为样本,通过PPM突变点识别模型,从高频时间序列中出现的众多"跳跃点"中甄别出能够改变时间序列波动趋势的突变点,对相邻两突变点之间样本进行Hurst指数分析,研究突发事件对国际原油期货价格波动的时间记忆性。研究表明,时间序列数据中存在多个"跳跃点",大多数跳跃点并未改变数据波动趋势,少数突变点不但改变数据波动趋势,国际原油期货价格波动受突发事件的影响改变其原有的运动轨迹。此项研究为后续学者提供了一种研究"事件冲击"和"数据时间记忆"的新方法。
突发事件;PPM变点;Hurst指数;石油期货
一、引言及文献综述
1973年石油危机以后,跨国石油公司对石油价格的垄断基本瓦解,石油价格成为波动最为强烈的商品,学术研究中出现大量关于石油价格波动特征的统计分析和宏观研究,石油逐渐成为具有金融属性的商品,进而衍生出石油期货等石油金融衍生品。尽管大量的学者对石油以及石油衍生品价格波动的统计特征进行统计分析,在各种假设条件下建立起多种描述波动特征的计量模型,但对价格未来趋势的预测结果不尽如人意,这是因为石油以及相关衍生品价格不仅仅受一般商品供求规律决定,石油由于其不可再生的特殊性,更容易受到地域性垄断地租的影响,形成垄断价格,价格波动脱离其自身价值波动。区域性的突发事件通过原油产量向石油以及石油衍生品市场传导,引起石油及衍生品价格波幅剧烈变化。
价格波动性的研究对衍生品定价、套期策略、生产与消费的决策和风险管理十分重要,国内外学者就价格波动性特征的研究大多集中在时变方差时间序列的研究上,Engle和Bollerslev相继提出ARCH和GARCH模型后,对时间序列波动率特征的研究引起学者们的关注,他们提出单整GARCH模型(IGARCH),该模型中条件方差的扰动会对将来各期的方差产生持续影响。Bollerslev和Mikkelsen(1996)提出了FIGARCH模型,从条件方差上反映时间序列的长期记忆特征。又由于EGARCH模型可以很好地体现金融价格波动的杠杆效应,并且以条件方差的对数形式确保能够取正值,使模型更加稳定,因此Bollerslev和Mikkelsen(1996)综合了FIGARCH和EGARCH模型,进一步提出了FIEGARCH模型。
Brennan(1985)假设商品价格服从随机游走过程[1]。后续学者在此假设基础之上假定资产价格变动率的条件均值和条件标准差随时间变化,即多因子资产价格变化模型。Schwart(1997)用期货价格检验了单因子模型、两因子模型和三因子模型的定价准确性,并用石油期货价格检验了长期均衡价格和现货价格之差,对石油期货价格进行了检验[2]。但并未考虑期货价格的跳跃性特征,其假定资产价格呈现连续变化,不会出现跳跃性。Jarrow和Rosenfeld(1984)认为资产价格波动的连续和非连续特征同时存在。Merton(1976)认为资产价格和收益率均存在厚尾分布和偏态分布现象,GARCH模型可解释收益率的偏相关性,但对收益率的跳跃现象无法进行解释。童汉飞和刘宏伟通过Jump-GARCH模型对中国沪深两市指数的跳跃性进行研究发现,Jump-GARCH比GARCH模型更加有效地估计出收益率和波动率的跳跃性变化[3]。
现有大量文献已证明金融实践序列具有波动率的长期记忆性和信息的非对称性[4-7]。刘建桥和孙文全通过沪深300指数期货每日结算价,研究了期货价格波动的不对称跳跃特征,发现沪深300仿真股指期货价格存在不对称跳跃波动,异常信息所导致的跳跃程度随时间变动[8]。
然而,期货价格波动包括由于基础价值变化所导致的基本性价格波动,和市场噪声交易者所引起的随机性波动两类[9]。类似的关于证券价格的研究包括Maheu和McCuedy(2004)认为,证券资产价格和收益率的波动由潜在的寻常信息和不寻常信息导致,寻常信息不会导致股价的跳跃性,股价的波动遵循一个平滑的过程,不寻常信息反应市场对为预期到的新信息的冲击,造成股价波动的跳跃性。Hsieh和Tauchen(1997)发现价格间断性存在于高频时间序列的波动中,突发事件对高频时间序列产生本质逆转效应。姚慧和范龙振发现石油期货价格有明显的跳跃特征和均值恢复特征[10]。Mu(2007)通过极端天气冲击美国天然气期货市场的研究发现,天气对天然气收益率和期货价格波动性产生显著影响。Linn和zhu(2004)发现库存信息发布对价格波动影响具有滞后期,即30分钟后市场交易建立新的平衡。
对于期货价格波动的研究主要集中在运用GARCH对期货收益率的波动聚集性上,GJR-GARCH模型和EGARCH模型将期货价格波动的非对称信息反映在条件方差中,无法说明期货价格波动带来的收益率所发生时间的间断性和非对称跳跃性。Sadorsky通过不同种类石油期货与各种计量模型的匹配发现,TGARCH模型适合于取暖油和天然气期货价格波动,GARCH适合于原油和无铅汽油的波动性[11]。Crosby对期货价格的跳跃性特征进行了理论分析[12]。Deng在资产价格模型中加入跳跃特征,利用电力期货价格数据进行实证分析[13]。赵华和王一鸣通过ARMAJI-GARCH模型分析金属期货的自相关性、条件异方差性和动态跳跃性,发现中国金属期货存在时变跳跃特征,但缺少对跳跃点之间的期货价格波动特征进行细化研究[14]。
现有学者研究国际油价及其衍生品价格波动规律文献的假设前提是时间序列的平稳性,即使遇到非平稳数据,通过一阶差分和二阶差分,滤去白噪声事件,使非平稳数据转化为平稳数据后进行一系列的研究。然而,差分后的平稳数据并不能全面地反映时间序列波动的本质,差分的结果是略去时间序列所包含的相关信息,这种研究方法并不能全面反映石油及其衍生品价格波动的规律,忽略突发事件对时间序列的影响,这也是大量学者预测油价而结果不尽如人意的原因。再者,现有关于跳跃点的研究以感性图示的方法或者分阶段尝试的方法多次进行拟合,寻找突变点的出现时间点,研究结果显示一段时间序列出现的跳跃点具有多重性。然而,众多的跳跃点并不能反映时间序列的本质“拐点”,具有较小影响的突发事件并不能对时间序列的趋势产生长期影响,能够改变时间序列长期趋势的事件必然改变跳跃点之间数据间的波动规律。
本研究建立在国内外关于高频时间序列数据“跳跃点”的文献基础之上,以石油期货价格高频数据为样本,在众多“跳跃点”中,通过PPM突变点分析模型甄选出真正能对时间序列未来发展趋势产生“质变”的跳跃点,并对两突变点之间的高频数据进行Hurst指数分析,目的是验证受重大事件影响的突变点对数据内在依赖性产生冲击,数据间的相关性发生改变。
二、数据来源
对高频数据进行突变点识别过程中,首先应该考虑的是信息的传递速度以及市场的结构,鉴于期货市场的参与主体具有多样性,能够较快对突发事件做出反应,本文以原油期货市场为例进行突变点识别和突变点之间数据的依赖程度变化的研究。鉴于数据的可得性,我们选取2014年10月交割的美国轻质原油期货数据,样本区间为2009年8月到2012年9月的日度数据。因证券收益率的分析更能够准确地反映证券价格波动的特征,在进行Hurst指数分析时,我们对期货价格数据进行对数处理。数据均来自于美国纽约商品交易所网站和瑞斯数据库。
三、研究方法
(一)PPM变点分析
变点是指在统计模型中某些变量的分布或数字特征发生了突然的变化,时间序列在突点前后所服从的分布发生变化。变点问题的研究把统计控制理论、估计和假设检验理论、非贝叶斯和贝叶斯方法、固定样本抽样和连续抽样方法结合起来。现有研究变点问题的文献均建立在特定的假设前提下,能够有效地判断出变点前后时间序列分布的变化,Dipak基于贝叶斯估计方法,在假定已知变点个数和位置的基础上估计了单参数指数分布族中的变点后验分布,类似的研究还有Ferreira和Broemeling的研究[15-17]。该方法过于主观地事先对变点位置进行了确定,对变点个数及出现的时间点过于人为主观化;Inclan和Tiao基于IT检验,对整个时间序列进行样本分割的前提下计算单个样本的变点,忽略了整体意义上的变点连续性问题[18];Hamilton(1989)提出的Markov机制转换模型能够捕捉时间序列在不同状态下的转换过程,但Markov机制转换模型要求结构变化内生,在时间上具有随机性和连续性,适合于拟合具有持续结构变化的时间序列数据。PPM变点分析模型是分析变点问题的动态模型,与已有文献研究变点问题的不同之处在于对变点时间和个数假定为未知量,PPM模型能够识别时间序列突变点,测算突变概率和后验均值。
假定x1,x2,…,xn为已知时间序列,指标集合I={1,2,…,n}。假设存在一个I的随机划分ρ={i0,i1,…,ib},其中0=i0 (1) 对所有的i、j∈I,i 时间序列x1,x2,…,xn的边缘分布密度函数为f1(x1|θ1),…,fn(xn|θn),其中θ1,θ2,…,θn表示未知参数。在区间ρ,对ir-1 根据Barry和Hartigan(1992)的研究成果,如果出现下列两种情况:一是ρ服从 p(ρ={x1,x2,…,xn}|x1,x2,…,xn)= p(B=b|x1,x2,…,xn)= (二)Hurst指数分析 Hurst指数由水文专家H.E.Hurst通过对尼罗河泛滥的847年数据进行记录后发现,尼罗河泛滥的流量并不具有随机性,较大泛滥流量之后出现更大的泛滥力度,偶然地出现低于平均流量的数据,泛滥流量之间存在循环性。 分形(Fractal)是通过对自然界中无规律、无法用欧几里得几何图像所表示的数据,寻找整体与部分之间的自相似性,与自相关性关系密切的是长相关性,表示数据之间的波动具有时间记忆特性。 布朗运动表示研究变量随机运动过程,变量运动轨迹遵循分形体结构,位置增量为独立的Gauss随机过程,变量进行布朗运动的位置是时间T的随机函数,Wiener对位置增量方差R和相对应的时间增量Δt研究后发现,R和Δt满足R=E[xt-x0]2=k(Δt)2H,H为Hurst指数,标准布朗运动的Hurst指数等于0.5,Mandelbrot将Hurst指数推广到0和1之间,即分数布朗运动。R/S方法是分形理论中一种常用方法,用于估计Hurst指数。 设时间序列{x1,x2,…,xt,t=1,2,…,T},将长度为T的时间序列分为n×k个长度为n的子区间,对累积极差R(n)和标准差S(n)进行计算。 区间长度n的变化导致重标极差Qn=R(n)/S(n)的变化,具有自相似性的xt,当n→∞时,Qn→c×nH,c为常数,H为Hurst指数。 当0 当H=0.5时,时间序列{x1,x2,…,xt,t=1,2,…,T}是相互独立、方差有限的随机时间序列,是标准的布朗运动,具有马氏链特性,过去的事件对未来不会产生任何影响。 当0.5 当H=1时,时间序列{x1,x2,…,xt,t=1,2,…,T}具有完全预测性,时间序列成直线分布,价格波动的数据完全可以用过去的数据进行预测。 利用PPM突变点识别法对2014年10月交割的美国轻质原油期货价格时间序列数据进行突变点识别,所得结果如图1和表1所示。 图1 2014年10月交割的美国轻质原油期货价格突变点识别图 图1中,上方表示原油期货价格的后验均值,下方表示后验均值所对应的后验概率。观察发现,2009至2012年间,原油期货价格受突发事件、市场干预、商业库存、国际金融投机和美元汇率等因素的影响,出现较多的波动跳跃点。然而,并不是所有的跳跃点都代表着原油期货价格时间序列的真正“拐点”,大多数波幅较大的拐点并未改变原有时间序列的长期波动趋势,我们设定后验概率大于0.3为时间序列波动的阀值,阀值是衡量数据本质发生变化的临界点,阀值点过后,时间序列数据产生新的均衡,两个阀值之间的数据围绕在新的均衡线上下波动,我们称能够改变数据未来趋势的阀值点为突变点,突变点之后的数据将改变原有的波动趋势,直到新的阀值点出现。在我们选取的样本中,后验概率大于0.3的突变点,如表1所示。 由表1可知,2009-2012年间共出现112次后验概率大小不一的突变点,后验概率较大意味着突发事件改变时间序列数据未来趋势的可能性较大,即突发事件的冲击足以改变国际社会对未来石油期货价格走势的预期。我们以后验概率大于90%为临界点,对原油期货价格时间序列进行分阶段研究突变后的数据,结果见表2。 如表2所示,以后验概率大于90%为临界点对2009-2012年美国轻质原油期货价格时间序列数据进行划分阶段处理。2009年8月24日至2012年9月28日期间,2010年5月5日至2011年3月11日之间的Hurst指数小于0.5,原油期货价格接近于随机游走,其它阶段均大于0.5,原油期货价格之间存在偏相关性,且不同阶段偏相关性大小存在差异性。 表1 2014年10月交割的美国轻质原油期货价格突变点识别 表2 2014年10月交割的美国轻质原油期货价格动态相关性研究结果 图2 美国1960-2011年石油消费弹性系数变动图 石油消费和经济发展水平密切相关,石油消费量会随着经济发展而持续增加。我们用石油消费弹性系数来表示经济增长与石油消费增长之间的关系,石油消费弹性系数=石油消费增长率/GDP增长率。短期而言,突发事件导致的石油供给减少、石油价格上涨均会破坏石油消费弹性系数的稳定结构。对于长期而言,在一段较长时期内,石油消费弹性系数保持在一个相对稳定的区间。各国经济发展水平、能源结构以及技术水平存在差异性,石油消费弹性系数不能进行横向比较,美国的石油消费弹性系数在0.3~0.5为正常波动区间。如图2所示,RATESY、RATEGDP和ESY分别表示美国石油消费增长率、美国国内生产总值增长率和美国石油消费弹性系数,总体来看,石油消费增长和国内生产总值增长保持相对稳定的波动轨迹,国际上发生次贷危机和欧债危机后,美国石油消费出现剧烈波动,带动石油消费弹性系数发生波幅较大的剧烈震动。次贷危机和欧债危机导致国际原油需求量的迅速减少,油价的波动向石油期货市场转移,2009年原油期货价格变点现象17次,12月7日后验概率大于0.90,Hurst指数短时间内由0.693 6下降到0.595 9,这是由于欧债危机导致国际社会对原油价格预期出现逆转,受美国次贷危机复苏的影响,对原油价格复苏预期抱有极大期望,欧债危机作为突发事件扰乱社会对原油价格的预期,原油期货价格亦受影响,每日价格波动之间的偏相关性减弱,接近随机游走状态。 图3 2010年剔除美元汇率影响因素后的国际原油价格波动轨迹 观察图3发现,美国实行量化宽松货币政策之前,美元汇率对国际石油价格影响不大,政策实施后,通过剔除汇率影响因素后发现,国际原油价格波动相对平缓。2010年,美国实施大规模量化宽松货币政策,美联储的做法无异于全力开动“印钞机”,意味将大量流动性重新投入市场,势必导致美元的大幅贬值,同时带来资产泡沫,并加大美国国内通货膨胀的风险。美元作为石油市场的权威标价和结算货币,美国只需用本国货币可购买别国必须付外汇才能购得的石油,从而使美国在国际贸易中的巨额赤字大幅减少,可免受汇率波动对其实际支付数额的影响。美国量化宽松货币政策导致国际金融市场的美元汇率波动,美元汇率通过风险溢出加剧国际石油价格的波动。同时发现,油价的波动风险增加。2010年出现变点现象37次,大部分突变点后验概率大于0.50,Hurst指数再次由0.718 0下降到0.572 1。美国量化宽松货币政策对石油市场的突发性冲击再次扰乱社会对原油价格的预期,石油期货价格之间的偏相关性减小,2010年5月5日至2011年3月11日出现原油期货价格走势逆转的预期现象。 图4 国际原油价格走势及突变点标志性事件 1991年海湾战争带来油价的高涨短暂性升高,战争结束使油价迅速重归平稳。1998年亚洲金融危机导致国际社会对石油的需求量迅速减少,油价跌至最低点12.28美元/桶,由于OPEC采取持续减产政策,致使油价迅速提升。2001年,“911”事件使国际油价再度受挫,但随着美国对阿富汗和伊拉克的战争,国际油价又开始新一轮上涨,从2003年委内瑞拉石油工人罢工、2005年墨西哥湾飓风事件对国际油价的影响可以看出,每一次石油供给减少都将打破国际油价原有趋势,国际油价达到一个新的高度后形成新的趋势。美国次贷危机和欧债危机再次重创国际油价,之后各国采取的经济回暖政策再次拉高油价。2011年欧债危机不断发酵,美债问题波澜迭起。西亚北非的政局动荡也使得国际油价波动明显,新兴经济体面临经济增速放缓和通货膨胀的双重压力,经济复苏的长期性、艰巨性和复杂性更加凸显,2011年共出现突变点40次,受国际社会对油价的预期影响,石油期货价格再次向随机游走转移。2012年受经济复苏的影响,原油期货价格逐渐摆脱前期突发事件的影响,石油期货价格之间的偏相关性逐渐增强。 本研究以美国轻质原油期货价格为例,研究高频时间序列突变点的识别问题,是针对高频时间序列出现多处“拐点”而非本质突变的现象,突变点前后数据之间的偏相关性改变,样本数据之间的依赖性强弱发生改变。研究中,我们运用PPM突变点识别模型对美国轻质原油2014年10月交割的期货价格波动数据进行突变点识别,以后验概率大于90%为临界点将样本数据进行分割,研究发现,国际上重大的突发事件均对原油期货价格波动数据产生影响,且这种影响具有长期记忆性,突变点前后的数据出现偏相关性拐点,改变了原油期货时间序列的波动趋势,每一次重大历史事件均改变了高频时间序列的原有均衡,事件过后产生新的均衡。 [1]BrennanJ,SchwartzE.EvaluatingNaturalResourceInvestment[J].JournalofBusiness,1985(2). [2]SchwartE.TheStochasticBehaviorofCommodityPrices:ImplicationforValuationandHedging[J].JournalofFinance,1997(3). [3]童汉飞,刘宏伟. 中国股市收益率与波动率跳跃性特征的实证分析[J].南方经济,2006(5). [4]KangSH,YoonS.LongMemoryPropertiesinReturnandVolatility:EvidencefromtheKoreanStockMarket[J].PhysicaA, 2007(3). [5]AdnanK,SaadetK,ErdostT.DualLongMemoryPropertyinReturnsandVolatility:EvidencefromtheCEECountries'StockMarkets[J].EmergingMarketsReview,2009(2). [6]马超群,刘超,李红权. 上海金属期货市场的非线性波动特征研究[J].财经理论与实践,2009(1). [7]张作云. 国际金融和经济危机后我国发展面临的挑战[J].管理学刊,2014(3). [8]刘建桥,孙文全. 沪深300仿真股指期货价格不对称跳跃波动的实证分析[J].数理统计与管理,2010(11). [9]黄卫东. 人民币与美元相互可兑换状况分析与政策建议[J].管理学刊,2015(1). [10]姚慧,范龙振. 石油价格跳跃下期货价格动态模型及实证分析[J].系统工程学报,2011(2). [11]SadorskyP.ModelingandForecastingPetroleumFuturesVolatility[J].EnergyEnomics,2006(4). [12]CrosbyJ.Amulti-factorsJump-diffusionModelforCommodities[J].QuantitativeFinance,2008(2). [13]DengS.StochasticModelofEnergyCommodityPricesandTheirApplication:Mean-reversionwithJumpsandSpikes[R].Berkeley:UniversityofCaliforniaEnergyInstitute,1998. [14]赵华,王一鸣. 中国期货价格的时变跳跃性及对现货价格影响的研究[J].金融研究,2011(1). [15]DipakKD,SujitKG,HangC.MeasuringtheEffectofObservationsUsingthePosteriorandtheIntrinsicBayesFactorswithPriorInformation[J].Sankhya, 1997(3). [16]FerreiraPE.ABayesianAnalysisofASwitchingRegressionModel:KnownNumberofRegimes[J].JournaloftheAmericanStatisticalAssociation, 1975(350). [17]BroemelingLD.SomeBayesianInferencesforAChangingLinearModel[J].Technimetrics,1980(22). [18]InclanC,TiaoGC.UseofCumulativeSumsofSquaresforRetrospectiveDetectionofChangesofVariance[J].JournaloftheAmericanStatisticalAssociation, 1994,89(427). InternationalCrudeOilFuturesPrices'MutationPointIdentificationResearch:BasedonPPMChangePointAnalysisandHurstIndexAnalysis ZHANGYue-sheng1,2 (1.SchoolofManagement,XinxiangUniversity,Xinxiang453003,China;2.SchoolofFinanceandEconomics,Xi'anJiaotongUniversity,Xi'an710061,China) Usingtheinternationalcrudeoilfuturespricefluctuation'sdaydataassamples,byPPMmutationpointrecognitionmodel,wecanfindmanyofthe"jump"identifymutationsinhighfrequencytimeseriesthatcanchangethevariationtrendoftimeseries,andthenanalysisthetwoadjacentmutationpoints'Hurstindex.Thisstudyshowsthatthetimeseriesdatahasmanymultiple"hop",mostofthejumppointsdidnotchangethedatafluctuationtrend,amutationpointnotonlychangeddatafluctuationtrend,alsotochangethedatadependence.Inthispaper,theresearchforsubsequentscholarsprovidesanewapproachtothestudyofthe"shock". emergency;PPM;Hurstindex;oilfutures 2016-03-02;修复日期:2016-06-14 教育部哲学社会科学研究重大课题攻关项目《新常态下中国经济运行机制的变革与中国宏观调控模式重构研究》(15JZD012);河南省哲学社会科学规划决策咨询项目《河南战略性新兴产业发展现状及对策研究》(2014D016) 张跃胜,男,河南延津人,博士生,副教授,研究方向:能源经济,信息经济。 F062.1 A 1007-3116(2016)08-0078-07 (责任编辑:张治国) 【统计应用研究】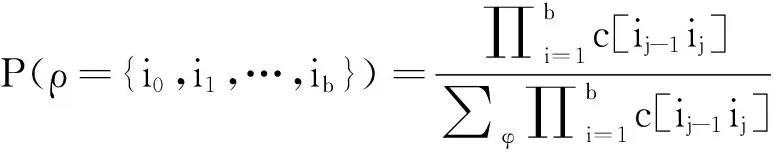


四、实证结果分析





五、结 论

