基于Origin的牛顿环实验仿真

曹卫军



基于Origin的牛顿环实验仿真

曹卫军

（昌吉学院 初等教育学院，新疆 昌吉 831100）

根据光的干涉原理，以牛顿环干涉实验为例，介绍利用Origin软件实现光学实验仿真的方法．通过改变凸透镜曲率半径、介质折射率、入射光波长和薄膜厚度等参数，观察到等厚干涉图样的相应变化，为光学的理论分析与实验教学提供便利．该方法避免了复杂的编程，实现过程简便易学．

Origin；牛顿环；等厚干涉；仿真

牛顿环等厚干涉是光学中的重要内容，教学中对于凸透镜曲率半径、入射光波长、介质折射率和介质薄膜厚度改变时对干涉条纹的影响解释比较抽象，学生不容易理解和接受，而在实验室实现这些变化也很困难．光学实验精度受到很多因素的影响，仅就用牛顿环测量透镜曲率半径来说，鉴于实验装置和实验者的操作水平，实验结果也往往存在很大误差．因此，诸多学者用计算机对光的干涉现象进行模拟[1-10]，达到了较为满意的教学效果．可是，初学者如果没有编程基础，想成功模拟光学实验存在一定难度．根据光的干涉理论，尝试用Origin仿真牛顿环干涉实验，得到了与文献[5-6]相同的结果．Origin能将矩阵元值的大小映射为灰度图，数值越小越偏于黑色，数值越大越偏于白色，所以Origin软件可以把表征光强的数据矩阵转换为反映干涉结果的计算机模拟图样．Origin的编程界面友好直观，避免了复杂的编程，实现过程便捷，易学好用，与Matlab，Maple等软件仿真相比优势明显．

1 牛顿环等厚干涉原理

1.1 牛顿环实验原理

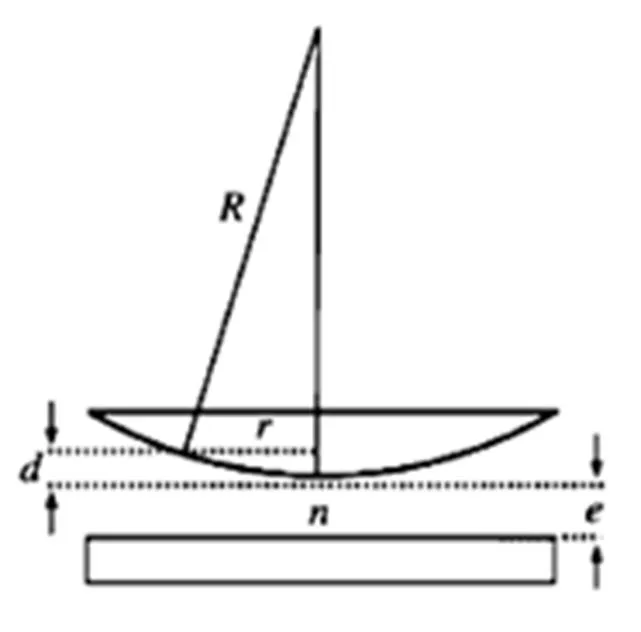
图1 牛顿环实验原理

考虑到半波损失，空气膜上、下表面发射的两束光的光程差为

1.2 相对光强公式推导

牛顿环干涉是分振幅的等厚干涉，两列相等振幅的相干光叠加在某点处，其光强[3]46分布为

即

相位差与光程差的换算关系为

把式（2）代入式（5）得

2 牛顿环干涉实验仿真

2.1 实验参数设置

2.2 实验仿真

启动0rigin7.5[11]，在任务栏依次点击File-New-Matrix，建立矩阵，设定参数，其中坐标范围 （-0.003，0.003）、矩阵维数（501，501），之后打开矩阵元值录入窗口，依据光强分布公式对矩阵元的值进行设定为：4*I0* （sin（（x^2+y^2）*n*pi/（R*λ）+2*pi*n*e/λ））^2．根据参数表，换算到国际单位，先代入第1组数值，点击OK，得到一个表征干涉光强的数据矩阵．任务栏中点击Plot菜单的profile／image，获得仿真结果．然后，依次修改参数，得到系列仿真图．

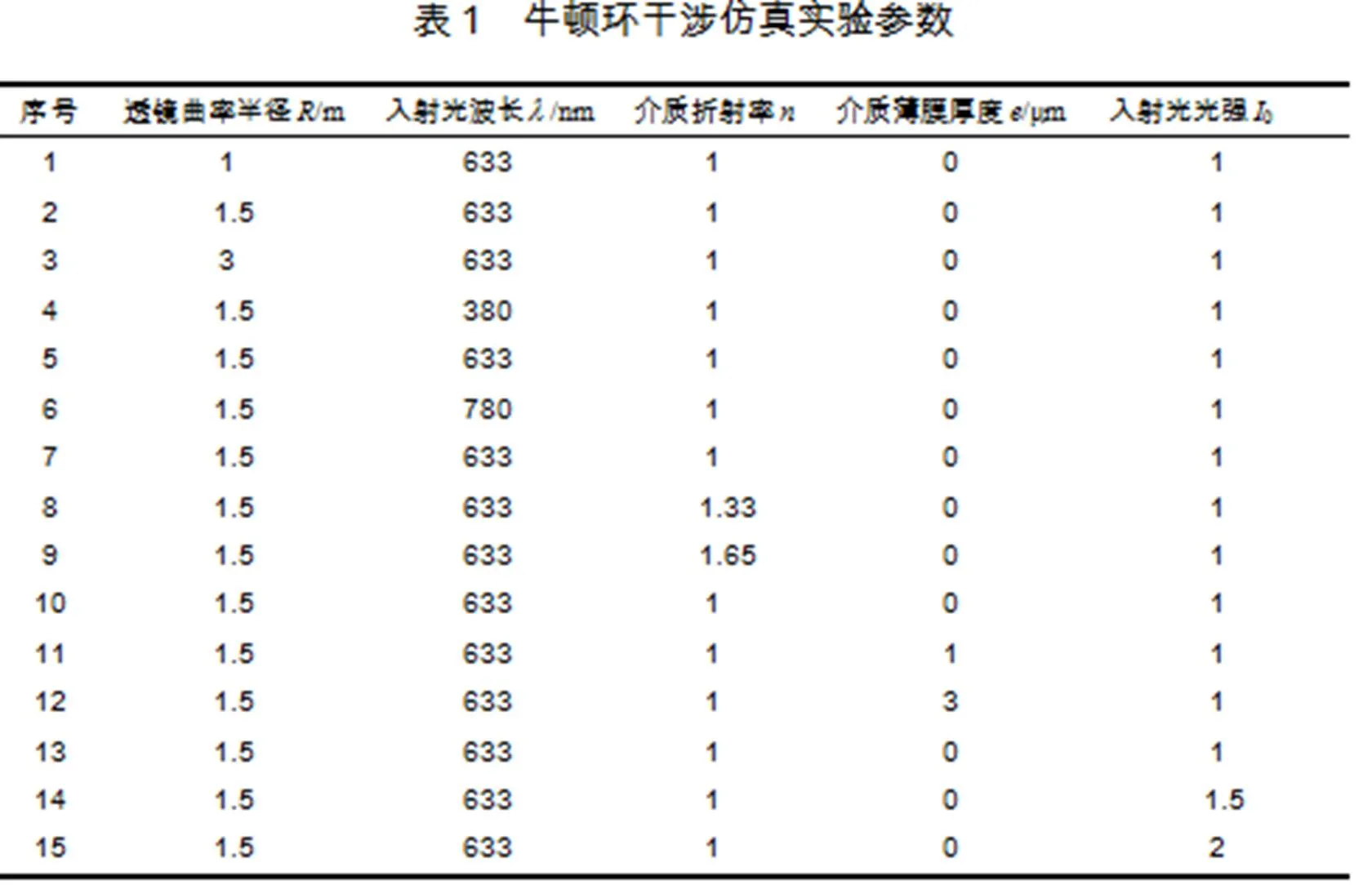
图2 凸透镜曲率半径与干涉条纹的关系

2.2.1 凸透镜曲率半径与干涉条纹的关系 表1中序号1~3组参数中，其他参数一定时，依次改变凸透镜的曲率半径，分别为1，1.53 ｍ，可以得到图2中（1）~（3）所示干涉图样．从图2可以看出，干涉条纹是一组同心圆环，在焦平面上呈明暗相间的稳定的不等间距的分布，内疏外密．但干涉条纹随着曲率半径的增加逐渐变疏，间距增大，中央黑斑也逐步变大．由可知，各级条纹半径随着的增大而增大，在相同的区域内出现的条纹级数减少．干涉条纹中央的明暗不发生变化，理论分析可知，当时，条纹中央处光程差，满足干涉相消条件，为暗环，以下同．

2.2.2 入射光波长与干涉条纹的关系 表1中序号4~6组参数中，其他参数一定时，依次改变入射光波长为380，633，780 nm，可以得到图3中（4）~（6）所示干涉图．不难看出，条纹随着入射波长的增大逐渐变疏，中央暗斑也逐渐变大，各级条纹半径也随之增大，在相同区域内能呈现的条纹级数减少．

图3 入射光波长与干涉条纹的关系

2.2.3介质折射率与干涉条纹的关系 表1中序号7~9组参数中，其他参数一定时，依次改变介质的折射率，分别为1（空气）、1.33（水）和1.65（液溴），可以得到图4中（7）~（9）所示干涉图样．对比发现，条纹随着介质折射率的增加逐渐变密，中央暗斑也逐渐变小，当增大时各级干涉条纹半径则变小，在相同区域内能呈现的条纹级数增多．

图4 介质折射率与干涉条纹的关系

2.2.4 薄膜厚度与干涉条纹的关系 表1中序号10~12组参数中，其他参数一定时，依次改变空气薄膜的厚度，分别为013 µm，可以得到图5中（10）~（12）所示干涉图样．对比分析发现，随着空气薄膜厚度的增加，条纹的疏密程度不变化．但干涉图样中央的明暗程度发生了变化，与图中光强分布曲线相对应．其原因是随着不再等于零，牛顿环变为非接触性牛顿环，条纹中央处光程差也在发生变化．

图5 薄膜厚度与干涉条纹的关系

2.2.5 入射光强与干涉条纹的关系 表1中序号13~15组参数中，只改变入射光的光强，其它参数保持不变，得到图6中的（13）~（15）所示干涉图样．随着的增加干涉条纹的形状、疏密均没有发生变化．从光强分布曲线可知，（13）～（15）显示相干光最大强度分别为4，6，8，均为入射光光强的4倍．当增大或减少时，相干光光强也随着等倍数增大或减少，但干涉条纹可见度不会发生变化，这是因为，改变时仍然是等振幅干涉，由可见度公式[12]可知，等振幅干涉可见度等于1．

图6 入射光光强与干涉条纹的关系

3 结论

综上所述，用Origin软件仿真牛顿环干涉实验，获得的仿真图像逼真，并可以绘制出实际实验中观察不到的光强分布图，增加了教学内容的表现力．掌握干涉原理以后，实验仿真过程简单，便于探究和验证物理规律，可激发学生的学习兴趣，获得教好的学习效果．

[1] 李剑波，覃泽涛．牛顿环实验的虚拟现实[J]．广西工学院学报，2001，12（3）：19-22

[2] 周党培，陈业仙．牛顿环实验的计算机仿真[J]．四川兵工学报，2009，30（7）：139-141

[3] 撒凤杰，蔡建乐，张飞刚．基于虚拟现实技术的牛顿环实验设计[J]．实验室研究与探索，2009，28（4）：46-48

[4] 吴学科，龙金．基于MATLAB的牛顿环的模拟研究[J]．凯里学院学报，2010，28（6）：50-51

[5] 汤剑锋，赵凡，欧阳锡城．应用Maple仿真模拟光学干涉实验[J]．湖南文理学院学报：自然科学版，2011，23（2）：77-81

[6] 谭毅．牛顿环实验的仿真研究[J]．信息技术，2011（5）：27-29

[7] 李晨璞，谢革英，胡金江，等．基于LabVIEW的牛顿环实验动态仿真[J]．实验室研究与探索，2013，32（6）：97-101

[8] 陈志歆，李斌．基于Matlab GUI的牛顿环仿真课件制作[J]．实验科学与技术，2013，11（4）：330-333

[9] 王蕴杰．基于Matlab的牛顿环白光干涉实验仿真[J]．大学物理实验，2014，27（4）：97-99

[10] 刘海顺，杨卫明．基于Monte-Carlo和Visual Basic的牛顿环实验模拟[J]．物理教师，2015，36（2）：95-97

[11] 周剑平．Origin实用教程（7.5版）[M]．西安：西安交通大学出版社，2005

[12] 姚启均．光学教程[M]．4版．北京：高等教育出版社，2008

Simulation study of the Newton ring experiment based on Origin

CAO Wei-jun

（School of Elementary Education，Changji University，Changji 831100，China）

Taking Newton′s ring experiment for example，a new method based on Origin was presented to simulate optical experiments according to the interference theory of light．It is observed that the fringe of equal thickness interference will change by adjusting the parameter of convex lens′ curvature radius，refractive index of medium， incident wavelength，and thickness of medium，etc．This method is not only easy to learn but also convenient in its process，which avoids the complex programming and facilitates the optical theory analysis and experimental teaching.

Origin；Newton′s ring；equal thickness interference；simulation

O431.1

A doi：10.3969/j.issn.1007-9831.2016.01.011

2015-10-30

新疆维吾尔自治区教研基金立项资助项目（新教高[2011]31号）

曹卫军（1969-），男，湖南双峰人，副教授，硕士，从事大学物理、强激光场与物质相互作用的研究．E-mail：993926463@qq.com