基于集合经验模态分解法的局部放电信号去噪

尚海昆，王　坤，李　峰

(1东北电力大学 电气工程学院，吉林 吉林 132012；2.国网新疆电力公司 电力科学研究院，新疆 830011)



基于集合经验模态分解法的局部放电信号去噪

尚海昆1，王坤1，李峰2

(1东北电力大学 电气工程学院，吉林 吉林 132012；2.国网新疆电力公司 电力科学研究院，新疆 830011)

针对局部放电检测中存在较多白噪声干扰的问题，采用基于集合经验模态分解的方法对放电信号进行消噪处理。该方法首先利用集合经验模态分解(EEMD)把信号分解成多个经验模态函数分量(IMFs)，然后利用3σ法则对各分量进行细节信息提取和能量估计，最后对IMF分量进行PCA变换，并根据IMF所含噪声能量选择主成分分量进行重构。EEMD建立在经验模态分解(EMD)基础之上，通过人为添加白噪声成分，并利用多次重复取均值的方式去除白噪声，同时抑制模态混叠现象。仿真数据分析表明，所提消噪方法可以有效抑制局部放电噪声干扰，成功提取出有效的局部放电信号。

EEMD；PCA；局部放电；消噪

局部放电检测作为评估高压电气设备绝缘状况的重要手段，在电气设备在线监测系统中发挥着重要作用[1-3]。局部放电信号非常微弱，而设备现场运行环境下存在较大的噪声干扰[4]。为得到真实可靠的放电信号，必须采取有效措施对现场干扰进行抑制。

目前用于局部放电监测的消噪方法有很多种，其中小波分析由于其良好的时频分辨特性，非常适合于处理非平稳信号，在局部放电信号消噪中得到了广泛的应用[5-7]。然而小波消噪需要预先选定小波基和分解层数，且消噪过程仅进行简单的小波系数收缩，未考虑小波系数在各尺度间的相关性，从而损失了部分重要的信息，并不能全面描述原始信号特征。

经验模态分解(Empirical Mode Decomposition，EMD)是一种数据驱动的自适应信号分解方法，可以把数据分解成具有物理意义的一组内蕴模态函数(Intrinsic mode function，IMF)分量。与小波变换相比，EMD无须事先给定小波基和分解层次，而是根据信号特性通过迭代的方式自适应地获取，基底和分解层次随信号的不同而改变[8-10]。然而EMD对含有突变信号的平稳信号进行分解时会产生模态混叠现象[11]。因此在分解含有窄带干扰的局部放电信号时，放电信号的突变性会使得某些IMF中仍然含有窄带和局放成分，两者无法有效分离。

集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)是Huang等人在EMD基础上提出的一种改进方法[12-14]。该方法在信号中人为添加白噪声成分，使信号的不同频率尺度被自动投影到均匀空间的频率尺度上，最后通过重复取均值的方式消除所添加的白噪声成分。该方法能够最大限度的保留原始数据序列的真实信息，并且在消噪的同时有效抑制模态混叠现象，分解出更为精准的IMF分量。

为了强化消噪效果，文中利用主成分分析(Principal Component Analysis，PCA)进一步对EEMD分解后的IMF分量进行消噪处理。主要思想是根据3σ法则准确估计每层IMF中所含噪声的能量，然后利用PCA对各层IMF进行分解[15，16]，并根据IMF中噪声所占的能量比例，选择合适个数的主成分分量进行重构，从而有效去除IMF中的噪声。

本文提出的EEMD消噪方法有效结合了EEMD和PCA方法的优良特性。文中将该方法用于抑制局部放电信号检测中的噪声干扰，并与传统的EMD以及EEMD方法进行对比。仿真数据分析验证了该方法的有效性及优越性。

1　EEMD

EEMD是建立在EMD基础之上的一种改进方法。EEMD 的算法结构与EMD算法基本相同。由于在EMD分解过程中出现模态混叠现象，Huang等人在EMD分解过程中给原始信号添加一个高斯白噪声信号，然后通过重复取均值的方式消除所添加的白噪声成分。该方法能够在消噪的同时有效抑制模态混叠现象，分解出更为精准的IMF分量。算法步骤如下：

(1)给原始信号x(t)叠加一组高斯白噪声信号n(t)：

X(t)=x(t)+n(t) .

(1)

(2)对X(t)进行EMD分解，得到各阶IMF分量：

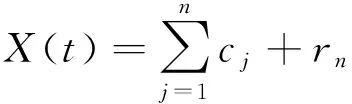
(2)

(3)给原始信号加入不同的白噪声ni(t)，重复步骤(1)和(2)

(3)(4)利用高斯白噪声的零均值原理，消除高斯白噪声作为时域分布参考结构带来的影响，原始信号对应的IMF分量可表示为：

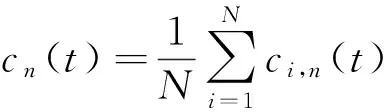
(4)

(5)原始信号最终分解为：

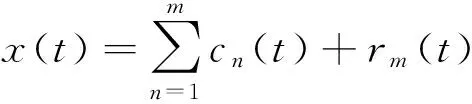
(5)

2　主成分分析

(1)对原始数据进行标准化，相关系数矩阵设为：

R=X′X ，

(6)

(2)通过奇异值分解，得到：

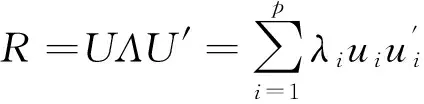
(7)

其中，Λ=diag(λ1，λ2，…，λp)，λ1≥λ2≥…≥λp>0，U=(u1，u2，…，up)为正交矩阵，u1，u2，…，up是与λ1，λ2，…，λp相对应的单位特征向量。

(8)

取前k个主成分q1，q2，…qk。

3　细节信息提取和能量估计

对于EEMD分解算法，通常认为第一层IMF全部由噪声构成。然而经过研究发现，imf1中仍含有一定量的信号细节信息。因此必须提取其中的信号细节信息来提高消噪效果。由于imf1中噪声占绝大部分，仅含有少量的信号细节信息，且所含噪声近似服从零均值正态分布。因此本文采用“3σ法则”进行细节信息提取。imf1满足加性噪声模型imf1=y1+n1，且n1-N(0，σ12)。根据“3σ法则”，噪声n1落在[-3σ，3σ]之间的概率为99.73%，即认为落在[-3σ，3σ]之外的imf1含有显著的细节信息，需要予以保留。对imf1进行细节信息提取，表示为：

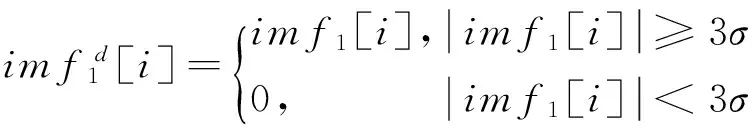
(9)

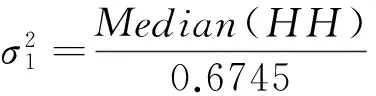
由此可计算imf1所含噪声的能量：

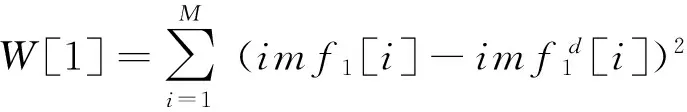
(10)

假设imfk(k≥2)所含噪声的能量为W[k]，则imfk中所含噪声能量由下式给出：

(11)

其中β≈0.719，ρ≈2.01。

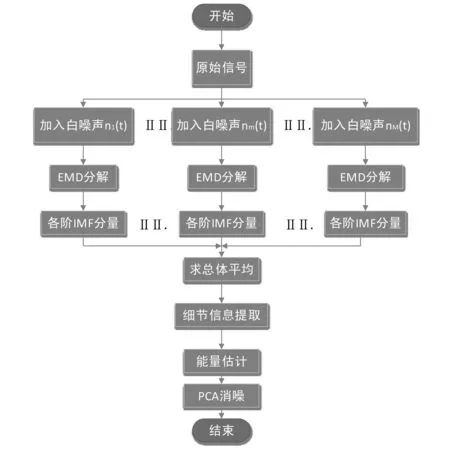
图1　EEMD-PCA消噪流程

4　EEMD-PCA信号消噪方法

EEMD-PCA消噪方法的基本步骤如下：

(1) 对原始信号进行EEMD分解，得到各层IMF分量。

(2) 对imf1采用“3σ法则”提取信号细节信息。

(3) 根据式(10)求imf1所含噪声的能量，并利用式(11)估计imfk(k≥2)中所含噪声的能量。

(4) 对imfk(k≥2)进行PCA分解，确定累计贡献率，进行重构去噪。

基于EEMD-PCA算法的消噪流程如图1所示。

5　仿真实验分析

5.1仿真信号

现场检测到的局部放电信号多为衰减振荡型脉冲信号，可以用以下两种数学模型来等效[8]：

(1)单指数衰减振荡波形

s1(t)=Ae-t/τsin2πfct .

(12)

(2)双指数衰减振荡波形

s2(t)=A(e-1.3t/τ-e-2.2t/τ)sin2πfct .

(13)

式中：A为信号幅值，τ为衰减系数， fc为振荡频率。

如图2(a)所示，取采样频率为50 MHz的4个局部放电仿真脉冲信号，幅值分别为1 mV、0.1 mV、1 mV、0.2 mV，衰减系数分别为0.1 us、0.05 us、0.1 us、0.05 us，振荡频率fc分别为15 MHz、20 MHz、20 MHz、10 MHz。取采样点数为800。

现场监测局部放电信号受窄带干扰及白噪声干扰的影响较为严重。为模拟现场真实局部放电信号，给仿真信号叠加窄带干扰以及白噪声。其中白噪声满足高斯分布N(0，0.022)。染噪信号如图2(b)所示。

图2　局部放电仿真信号

5.2EMD分解

对含有噪声的局部放电信号进行EMD分解，得到如图3所示结果。

图3　局部放电信号EMD分解

由图3可见，含噪声的局部放电信号经EMD分解后得到8个IMF分量和1个剩余分量。IMF分量频率由高到低向下排列，其中imf1分量频率最高。由图分析可知，EMD分解后的IMF分量中存在较为严重的模式混叠现象，部分IMF无实际物理意义，无法准确分析信号本质。

5.3EEMD分解

对含有噪声的局部放电信号进行EEMD分解，其中加入高斯白噪声标准差为0.1，加入次数为100，得到如图4所示结果。

图4　EEMD分解结果

通常认为，分解结果中的前几个 IMF 分量包含了原始信号的主要特征，并且认为第 1 个 IMF 分量代表了高频噪声的特征。但是由图3和图4分解结果可以看出，imf1分量包含明显的信号细节信息，为了达到更好的消噪效果需要进一步进行细节信息提取。

文中通过算法的运行时间(T)与正交性指标(IO)来评价EMD和EEMD的算法效率。IO定义如下：

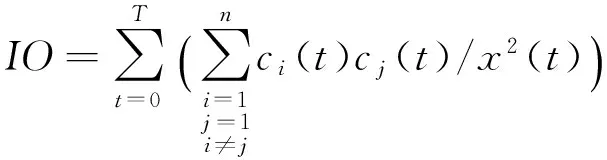
(14)

其中IO值越小，精度越高。算法的对比结果见表1所示。

表1　算法对比结果

由表1可知，虽然EEMD耗时较高，但其IO值得到有效提高。由图4和表1综合分析可得，EEMD能够有效分解出原始放电信号的各个组分，抑制EMD的模式混叠现象，具有更大的优势。

5.4消噪结果分析

为了对比仿真信号消噪效果，本文分别利用EMD算法、EEMD算法以及EEMD-PCA算法对仿真信号进行消噪处理。

本文采用信号的信噪比SNR及均方误差MSE对信号的消噪质量进行量化分析。SNR越高表明噪声消除的越彻底；MSE越小，说明消噪后的信号与原信号越相似，消噪质量越高。

SNR的计算公式为：

(15)

MSE表示为：

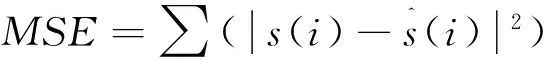
(16)

不同消噪方法进行消噪后的时域效果见图5所示。

由图5(a)可见，EMD消噪方法对于幅值较小的第二个放电脉冲无法识别，而且消噪后信号存在较强烈的振荡现象。由图5(b)可见，EEMD消噪方法有效抑制了消噪过程产生的振荡现象，但是仍无法识别第二个放电脉冲信号。图5(c)可见，EEMD-PCA算法消噪后能够有效识别所有的放电脉冲信号，且去噪后信号更具光滑性，减少了信号振荡。由此可得，EMD方法由于产生了模式混叠，造成消噪后信号产生振荡；而且消噪的时候未考虑imf1分量包含的细节信息，损失了部分重要的信息，缺乏有效信号的特征保持性；EEMD消噪方法通过叠加高斯白噪声，保证了信号的每一个固有模态函数在时域上的连续性，从而消除模式混叠现象，有效抑制了去噪产生的振荡失真，但由于该过程仍未考虑IMF分量包含的信号细节特征，故仍未能有效识别全部放电脉冲信号；EEMD-PCA方法利用“3σ法则”对imf1进行细节信息提取，并通过PCA方法消除IMF上的噪声能量，有效识别出了全部放电脉冲信号，具有良好的特征保持性。

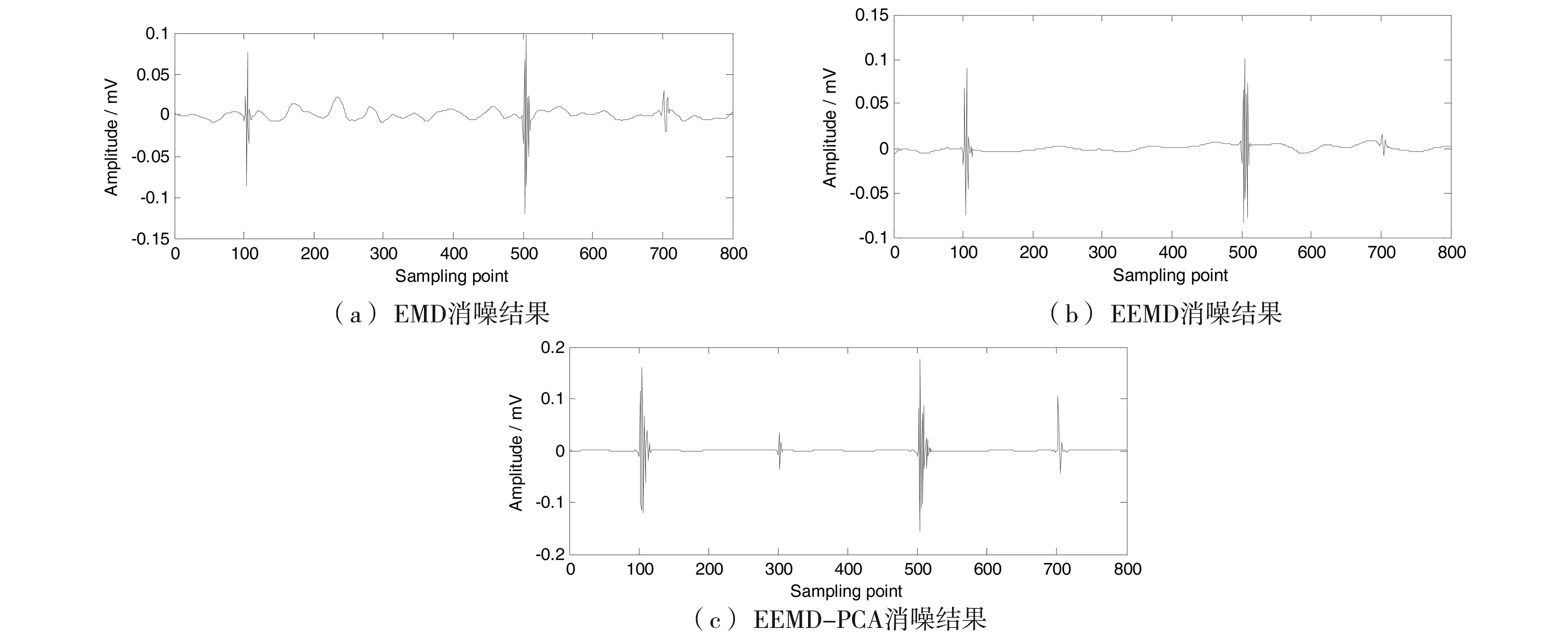
图5　信号时域消噪结果

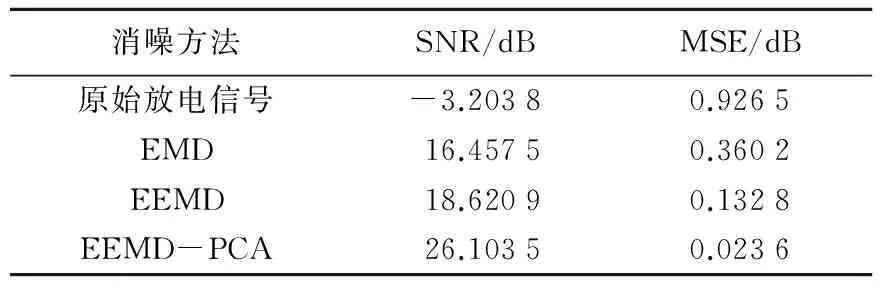
消噪方法SNR/dBMSE/dB原始放电信号-3.20380.9265EMD16.45750.3602EEMD18.62090.1328EEMD-PCA26.10350.0236

不同消噪方法消噪后的SNR和MSE结果见表2所示。

由表2可看出，EEMD-PCA方法消噪后，信号具有最高的信噪比和最小的均方误差，即EEMD-PCA方法的降噪效果最佳。这是由于该方法与EMD及EEMD方法相比，不仅消除了EMD产生的模式混叠现象，抑制信号的振荡失真，而且提取出了IMF分量上的细节信息，可以无损的描述放电信号特征，更加逼近真实放电信号。

6　结　　论

文中将EEMD方法用于局部放电信号消噪，取得了较好的应用效果。

(1)首先对信号进行EEMD分解，利用“3σ法则”对第一层IMF进行信号细节信息提取，然后计算各层IMF中所含噪声的能量，最后利用PCA对各层IMF进行分析，根据每层IMF中所含噪声的能量自适应确定应保留的主分量个数，实现信号与噪声的分离；

(2)由于EEMD加入白噪声，有效抑制EMD产生的模式混叠现象；通过细节信息的提取，有效保持了信号特征的完整性，使去除噪声后的信号更加逼近原始信号；

(3)仿真数据分析表明，文中提出的消噪方法有效抑制了局部放电信号的白噪声干扰，很好的保持了放电信号特征。

[1]李军浩，韩旭涛，刘泽辉，等.电气设备局部放电检测技术述评[J].高电压技术，2015，41(8)：2583-2601.

[2]郭俊，吴广宁，张血琴，等.局部放电检测技术的现状和发展 [J].电工技术学报，2005，20(2)：29-35.

[3]Ashtiani M B，Shahrtash S M.Partial discharge de-noising employing adaptive singular value decomposition[J].IEEE Transactions on Dielectrics & Electrical Insulation，2014，21(2)：775-782.

[4]唐炬，孙才新，宋胜利，等.局部放电信号中的白噪声和窄带干扰[J].高电压技术，2002，28(12)：8-10.

[5]唐炬，董玉林，樊雷，等.基于Hankel矩阵的复小波-奇异值分解法提取局部放电特征信息[J].中国电机工程学报，2015，35(7)：1808-1817.

[6]L.Satish，B.Nazneen.Wavelet-based Denoising of Partial Discharge Signals Buried in Excessive Noise and Interference [J].IEEE Transactions on Dielectrics and Electrical Insulation，2003，10(2)：354-367.

[7]唐炬，董玉林，樊雷，等.基于Hankel矩阵的复小波-奇异值分解法提取局部放电特征信息[J].中国电机工程学报，2015，35(7)：1808-1817.

[8]王文波，张晓东，汪祥莉.基于主成分分析的经验模态分解消噪方法[J].电子学报，2013,41(7)：1425-1430.

[9]辛鹏，赵阳，王忠义，等.基于经验模态分解的短期负荷预测[J].东北电力大学学报：自然科学版，2008，28(4)：57-61.

[10] Faiz J，Ghorbanian V，Ebrahimi B M.EMD-Based Analysis of Industrial Induction Motors With Broken Rotor Bars for Identification of Operating Point at Different Supply Modes[J].IEEE Transactions on Industrial Informatics，2014，10(2)：957-966.

[11] Yu L，Wang S，Lai KK.Forecasting crude oil price with an EMD-based neural network ensemble learning paradigm[J].Energy Economics，2008，30(5)：2623-2635.

[12] 陈可，李野，陈澜.EEMD分解在电力系统故障信号检测中的应用[J].计算机仿真，2010，27(3)：263-266.

[13] 朱宁辉，白晓民，董伟杰.基于EEMD的谐波检测方法[J].中国电机工程学报，2013，33(7)：92-98.

[14] 袁娜，朱永利，梁涵卿.结合矩形窗的EEMD局部放电信号去噪[J].电力系统及其自动化学报，2015，27(3)：54-58.

[15] H Bro R，Smilde A K.Principal component analysis[J].Analytical Methods，2014，6(4)：433-459.

[16] 段峰峰，王永滨，杨丽芳，等.基于主成分分析方向深度梯度直方图的立体视觉深度图特征提取[J].计算机应用，2016,36(1)：222-226.

Partial Discharge De-noising based on Ensemble Empirical Mode Decomposition

SHANG Hai-kun1，WANG Kun1，LI Feng2

(1.College of Electrical Engineering，Northeast Dianli University，Jilin Jilin 132012；2.State Grid Electric Power Research Institute，Xinjiang 830011)

To overcome the influence of white noise in partial discharge detection，a novel method based on Ensemble Empirical Mode Decomposition (EEMD) was proposed for signal de-nosing.By introducing extra noise into the decomposition process，EEMD can effectively separate the original signal into different intrinsic mode functions (IMFs) with distinctive frequency scales.Signal details in IMFs could be preserved with 3σ rule.Principal Component Analysis was then utilized for IMFs and principal components were extracted for reconstruction based on noise energy calculation.On the basis of EMD，EEMD is able to solve mode mixing problems through adding white noise manually.The results on simulated partial discharge signals show that the proposed signal de-noising technique can be effectively used for noise suppression and it can extract partial discharge signals successfully.

EEMD；PCA；Partial discharge；De-noising

2016-04-12

东北电力大学博士科研启动基金项目(BSJXM-201406)

尚海昆(1984-)，男，河北省保定市人，东北电力大学电气工程学院副教授，博士，主要研究方向：电气设备故障诊断及智能信息处理.

1005-2992(2016)04-0032-07

TM83

A