基于SIFT算法与Duffing振子的小电流接地选线
郭 威
(东北电力大学 电气工程学院,吉林 吉林 132012)
基于SIFT算法与Duffing振子的小电流接地选线
郭威
(东北电力大学 电气工程学院,吉林 吉林 132012)
对于小电流系统在发生单相接地故障时,提出一种基于Duffing振子信号检测技术与SIFT算法相结合的单相接地故障选线方法。由于受到高阻接地限制,传统的注入信号法有一定的局限性。Duffing 振子系统对信号具有非常高的敏感度,当系统的驱动力不同时,相图的轨迹也是不相同的,通过SIFT算法比较相图相似度,根据相似度大小作为选线判据。不受高阻接地限制,简化了选线过程,抗噪性能好,提高了选线的灵敏度。先通过电压互感器向故障系统相注入信号,然后通过探测器和滤波处理系统提取注入系统中的信号,将提取的信号输入到Duffing系统,通过系统相图相似度的大小准确判断出故障线路。
注入信号法;Duffing振子;SIFT算法;相图相似度
在我国的配电网中,小电流接地系统广泛得到应用,而在所有故障之中,单相接地故障概率最高,约占80%。配电网接线形式以及噪声会对微弱的接地故障信号产生干扰,使得故障选线的方法有一定的局限性[1-11]。
目前选线装置大多采用零序电流及其高次谐波原理实现故障选线,首半波法、有功分量法等其他方法也在应用[2]。小电流系统有一个重要的特征就是故障电流稳定分量幅值较小,无论是谐波分量还基波分量,都容易被干扰信号影响,二次侧的零序电流又会受到电流互感器的不平衡电流的影响。因此,基于谐波原理的装置在实际中会造成误判[3]。
本文采用注入式小电流Duffing振子法选线。Duffing振子对微弱周期信号感应十分的灵敏,当Duffing系统周期信号和它的内驱力的向量和满足一定条件时,系统相图会发生变化,SIFT算法是一种计算机视觉算法,用来侦测与描述相图的局部特征,在空间尺度中寻找极点,提取出位置、尺度、旋转不变量完成相图相似度计算,匹配速度快并且精确,通过识别相图相似度大小进行故障选线。Duffing振子与SIFT算法的相结合,使得选线具有良好的普适性。
1 注入信号法
正常运行时电压互感器二次侧各相电压幅值相等,当发生单相接地故障,故障相电压降为零,非故障相电压变为线电压,此时将信号注入到电压为零的相线之中,根据注入信号强弱和轨迹的形状判断故障线路及故障点所在的位置[4]。
注入信号是单相接地故障时暂时间的闲置状态的基地注入方法,没有增加任何其它一次设备,对于正在运行的设备也没有任何的影响,注入信号仅仅流向接地线路,效率较高,信号设备与一次强电流之间只是通过电磁耦合,没有直接电的联系,不涉及到绝缘问题,并且控制和信号发生设备都比较简单,装置的接线方式也很简单[6]。
对于提高注入法耐高阻能力有三种改进方法:降低注入信号的频率、应用注入信号的相位信息和应用双频信号。降低注入信号频率不但增大了消弧线圈的分流,而且耐高阻能力提升并不明显;注入双频信号又明显增加了系统的复杂度;所以采用故障线路与非故障线路注入信号相位差异进行选线。
2 混沌振子检测原理
本文中采用最为广泛的是Holmes型Duffing方程:

(1)
式中:k为阻尼比;-x+x3是系统非线性回复力; fcost为周期策动力, f取值不同时,系统运动轨迹不同。f=0时,由方程式得到相平面的鞍点(0,0)和焦点((±1,0),最终相点停留在两焦点之一。f≠0时, f值在逐渐增大的过程中,系统从同宿轨道到分岔轨迹,然后到混沌状态,再到混沌临界状态,最后到大尺度周期状态。
系统从混沌状态到大尺度周期状态系统相图有明显变化,此时周期策动力的幅值为临界值,设为fa。对上式进行尺度变换,取t=ωτ,待测信号为acos(ωτ+φ)。最终得到
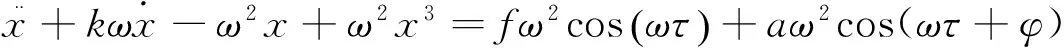
(2)
式中:ω为待测信号的角频,a为待测信号幅值;φ为待测信号与内驱力信号的相位差,化简式(2)得系统总的驱动力
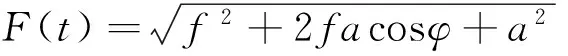
(3)
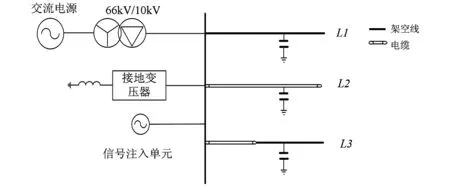
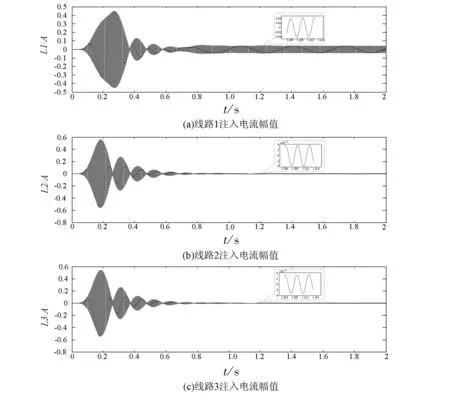
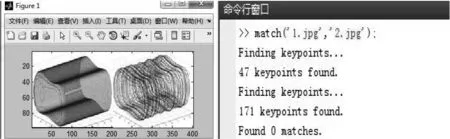
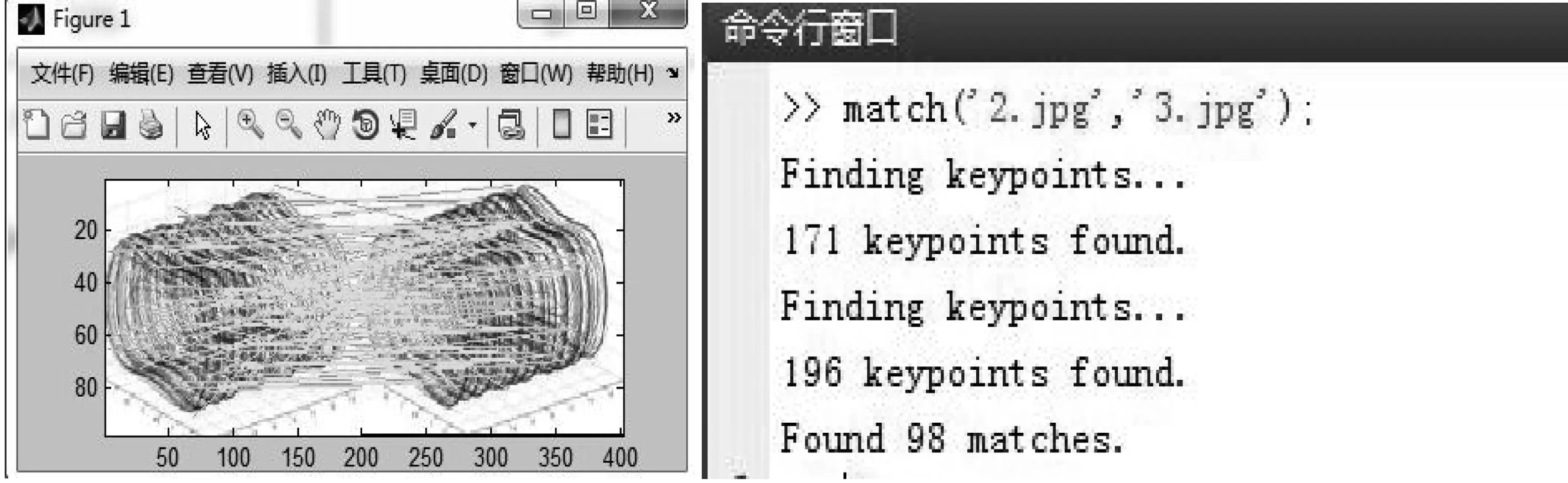
当F(t) (4) 当F(t)>fa时,即相角不在(4)式范围内,Duffing系统处于大尺度周期状态。 根据以上特点,可以将注入信号作为待测信号,与内驱力一起作为系统总的驱动力F(t)输入Duffing振子,得出相图。 SIFT主要包括4个步骤: (1)尺度空间极值检测 对于二维图像I(x,y),在不同尺度的尺度空间下表示L(x,y,δ)可由图像I(x,y)与高斯核G(x,y,δ)的卷积得到。建立图像的DOG金字塔,在DOG尺度空间中的26个领域中检测极值,D(x,y,δ)是两个相邻尺度图像之差,即: D(x,y,δ)=(G(x,y,lδ)-G(x,y,δ))*I(x,y)=L(x,y,lδ)-L(x,y,δ), 一个点如果与周围八个点以及上下层的十八个领域点共26个领域中是最大值与最小值,就确定该点是图像在该尺度下的一个特征点。 (2)利用特征点领域像素的梯度分布特征为每个特征点指定方向参数,使得算子具有旋转不变性质。 上式为(x,y)处梯度的模值和方向公式,式中L所用的尺度为每个特征点各自所在尺度。 (3)生成SIFT特征向量,把坐标轴旋转到特征点方向,保证旋转不变性,对每个特征点使用4×4共16种子点来描述,这样对于一个关键点可以产生128个数据,形成128维的SIFT特征向量,即特征描述符。 (4)特征点匹配是指在找出图像的特征点后,寻找图像间特征点的对应关系,通常采用最近领方法,查找每一个特征点在另一相图的最近领域,理想状态下两幅相图之间相同部分的特征点应该具有相同的特征描述向量,所以它们之间的距离应该最近。 (1)在配电网发生单相接地故障时,先根据电压变化确定故障相,向故障相注入信号。如果系统发生的是高阻接地故障,电压变化不明显,把信号注入到系统,确定配电网是否发生单相接地故障,如果发生接地故障,就将信号注入故障相。 (2)通过磁场探测法获取注入到系统之中的信号,此方法不受线路接线形式的影响,使用方便灵活。 .一是建立生态特别示范区。以目前张承地区的经济条件不可能靠其自身力量实现从贫困与生态恶化并存的局面向富裕与生态良好的方向转变,需要外部力量的介入,在区内实施特殊的财政、税收、技术等支持政策。在遵循生态和区域经济发展规律基础上,运用市场和行政手段通过体制创新、产业升级、城镇改造、资源开发利用方式转变等,建立生态型经济和社会功能体系。 (3)对Duffing系统进行设置,设k=0.5,由于线路对地有电容,非故障相也会流入一定的注入电流,所以在注入信号输入Duffing系统前,乘一个检测系数p,p是一个可以调节的变量,该调解可以根据测量到的电流值调节。当信号输入Duffing系统时,得到相图,用SIFT算法得到相似度,通过相似度的大小判断出故障线路。 仿真模型图如图1所示,该系统采用中性点经消弧线圈接地,消弧线圈采用过补偿方式,补偿度取10%。 图1 仿真模型示意图 选择3条馈线,如图1所示,其长度分别为20 km,4 km,20 km。线路的正序和零序参数如下: 架空线: R1=0.414 1 Ω/Km,R0=0.564 1 Ω/Km, L1=1.079 2 mH/Km,L0=7.392 4 mH/Km, C1=10.740 2 nF/Km,C0=4.209 nF/Km. 电缆: R1=0.305 Ω/Km,R0=0.453 23 Ω/Km, L1=0.305 3 mH/Km,L0=6.672 7 mH/Km, C1=196.2 nF/Km,C0=196.2 nF/Km. 线路1在0.02 s发生A相接地故障,接地电阻设为50 Ω,在0.5 s时将信号注入A相,线路会受到分布电容的影响,非故障相会流入一定的注入信号。测量3条线路A相注入信号电流如图2所示。提取的注入电流分别输入Duffing振子系统中,调整检测系数p和内驱力初相角,其相应Duffing振子相图变化情况如图3所示。 图2 电阻为50 Ω 3条线路注入电流值 图3 接地电阻为50 Ω Duffing系统输出相图 对接地电阻为50 Ω Duffing系统输出的三幅相图进行SIFT算法两两比较: 图4 线路一与线路二的匹配效果 根据图4得出下表,如表1所示。 表1 线路1与线路2的特征点 通过表1可以得出,线路1相图与线路2相图的特征点匹配数为零,相似度为零。 图5 线路1与线路3的匹配效果 根据图5得出下表,如表2所示。 表2 线路1与线路2的特征点 通过上表可以得出,线路1相图与线路3相图的特征点匹配数为零,相似度为零。 图6 线路2与线路3的匹配效果 图6中蓝色线为两个相图相匹配的点,根据图6得出下表,如表3所示。 表3 线路2与线路3的特征点 通过表3可以得出,线路1相图与线路3相图的特征点匹配数为98,相似度为58%。 通过SIFT算法对相图两两比较我们可以看出线路2与3相图的相似度远远大于线路1与2、1与3相图的相似度,因此可以得出线路1的相图不同于其他两条线路的相图,则判定为故障相,这与初始假设结果一致。 本文考虑到注入法在接地电阻不同时,故障线路与非故障线路注入信号的幅值与相角存在一定的差异。引入Duffing 振子检测系统对故障线路进行筛选,并用SIFT算法对相图进行了分析,仿真结果和我们假设的故障线路是一致的,验证了两者结合进行选线的有效性。 [1]张国军,韩静静,任荣,等.多判据融合小电流单相接地故障选线方法研究与实验[J].电工电能新技术,2015,34(4):56-61. [2]贾清泉,石磊磊,王宁,等.基于证据理论和信息熵的消弧线圈接地电网融合选线方法[J].电工技术学报,2012,27(6):191-197. [3]王建元,鞠默欣,徐志璇,等.基于HHT小电流接地故障选线与在线故障定位方法[J].电测与仪表,2014,51(15):48-54. [4]庞清乐,孙同景,钟麦英,等.基于粗集理论的小电流接地系统故障选线[J].中国电机工程学报,2007,27(4):60-64. [5]束洪春,彭仕欣,李斌,等.基于零序电流激励的谐振接地系统故障选线测后模拟方法[J].电工技术学报,2008,23(10):106-113. [6]林克正,张彩华,刘丕娥.基于分块主颜色匹配的图像检索[J].计算机工程,2010,36(13):186-188. [7]郭清涛,吴田.小电流接地系统故障选线方法综述[J].电力系统保护与控制,2010,38(2):146-152. [8]王宾,耿建昭,董新洲,等.配网高阻接地故障伏安特性分析及检测[J].中国电机工程学报,2014,34(22):3815-3823. [9]赖志慧,冷永刚,孙建桥,范胜波.基于Duffing振子的变尺度微弱特征信号检测方法研究[J].物理学报,2012,61(5):1-9. [10] 王永生,姜文志,赵建军,范洪达.一种Duffing弱信号检测新方法及仿真研究[J].物理学报,2008,57(4):2053-2059. [11] 戴武昌,严干贵,张秋鹏.DS证据理论在小电流系统的故障选线中的应用[J].东北电力大学学报,2007,27(6):19-23. Small Current Based on Duffing Oscillator and SIFT Algorithm Grounding Line Selection GUO Wei (Electrical Engineering College,Northeast Dianli University,Jilin Jilin 132012) In this paper,a method of single phase grounding fault line selection based on Duffing oscillator signal detection technique and SIFT algorithm is proposed for small current system in the event of a single phase to ground fault.Due to the high resistance grounding limit,the traditional injection method has some limitations.Duffing oscillator system has a very high sensitivity to the signal.When the driving force of the system does not at the same time,the trajectory of the phase diagram is different,and the phase diagram is compared with the SIFT algorithm.This method is not restricted by high resistance grounding,and simplifies the process of selecting the line,good noise immunity,and improves the sensitivity of the line.Firstly,the signal is injected into the fault system by the voltage transformer.Then the signal is extracted from the injection system by the detector and filter processing system.The signal input to the Duffing system can be determined by the size of the phase diagram of the system. Method of injection;Duffing oscillator;SIFT arithmetic;Similar of phase diagram 2016-06-18 郭威(1991-),男,吉林省松原市人,东北电力大学电气工程学院在读硕士研究生,主要研究方向:电力系统保护与控制. 1005-2992(2016)04-0026-06 TM726 A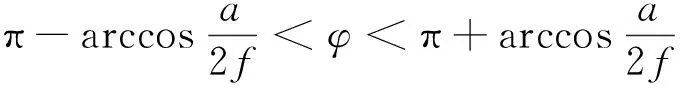
3 SIFT算法原理
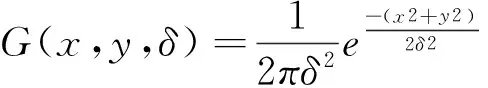
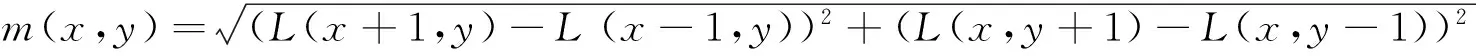
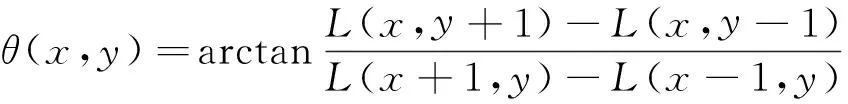
4 故障选线步骤
5 仿真验证





6 结 论

