一类二阶常微分方程初值问题解的性质的完全证明
张大鹏,薛 雯,朱秀丽,徐中海,
(1.东北电力大学 理学院,吉林 吉林 132011;2.东北电力大学 学报编辑部,吉林 吉林 132012)
一类二阶常微分方程初值问题解的性质的完全证明
张大鹏1,薛雯2,朱秀丽1,徐中海1,2
(1.东北电力大学 理学院,吉林 吉林 132011;2.东北电力大学 学报编辑部,吉林 吉林 132012)
在文献[1]的附录B中,研究了一类二阶常微分方程初值问题古典解的性质,并给出了相应的理论证明。作者认为该证明过程存在一些疏漏,鉴于其在文献[1]中的基础作用,本文给出其相应的完整证明。
二阶常微分方程;初值问题;有界
在文献[1]的附录B中,研究了如下问题
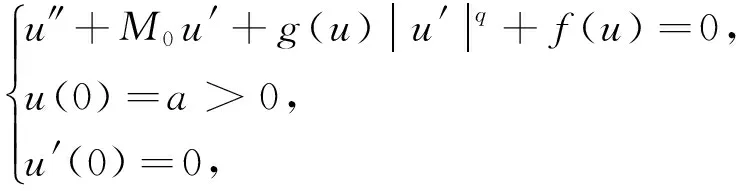
(BQ)
其中,M0>0, 0 (H1)g(t)≥0,在(-∝,0)∪(0,+∝)上光滑,在(0,+∝)上不增; (H2)f(t)>0,在(-∝,0)∪(0,+∝)上光滑,在(0,+∝)严格递减; 文献[1]中给出如下引理: 引理B设(H1)-(H3)成立,u(t)∈C2([0,R(a)))是问题(BQ)的经典解,其中(0,R(a))是解的最大存在区间。则 (1)u(t),u′(t)在(0,R(a))上严格递减; (7)R(a)≥G(a)。 解的存在性和光滑性可由文献[2]得到。 结论(1)的证明: r0=R(a)的情形。显然(1)获证。 r0 不妨设r0>0是u′(t)从0开始的第一个极小值点。则存在r1≤r0 产生矛盾。因此r0=R(a),则在(0,R(a))上u″(t)≤0,且u′(t)在(0,R(a))上严格递减。 结论(2)的证明: 结论(3)-结论(7)的证明同文献[1]。 文献[1]中的证明有下面几点疏漏: (1)r0的选取未作说明。事实上r0的选取应依照u′(t)的最大性严格单调区间长度,由于文献[1]中的疏漏,使得接下来的推理难以理解。 (2)即使把r0的选取理解为按u′(t)的最大性严格单调区间长度,文献[1]中的r1 (3)对选取r1、r2目的及选取条件未作任何说明,对反证法的结论未作任何解释,这使文章读起来晦涩难懂。 还需要指出的是,这个问题在文献[1]中的作用是基础性的,而且类似形式的问题在流体、特别是塑性流体的一些研究中起到一定的基础作用(见文献[3-12]),加之我们后面研究工作的需要,我们给出一个完整,顺畅的证明是必要的。 [1]Zhonghai Xu,Jiashang Zheng,Zhengguo Feng.Existence and regularity of nonnegative solution of a singular quasi-linear anisotropic boundary value problem with gradient terms[J].Nonlinear Analysis TMA,2011,74(3):739-756. [2]蔡燧林.常微分方程[M].3版.杭州:浙江大学出版社,2013. [3]A.Nachman and A.Callegari.A nonlinear singlar boundary value problem in the theory of pseudoplastic fluids[J].SIAM J.Appl.Math.,1986,38(2):275-281. [4]C A.Stuart.Existence theorems for a class of nonlinear integral equations[J].Math.Z.,1974,137(1):49-66. [5]S.D.Taliaferro.A nonlinear singlar boundary value problem[J].Nonlinear Analysis TMA,1979,3(6):897-904. [6]Zhang Zhijun,Jiangang Chen,Existence and optimal estimates of solution for singular nonlinear Dirichlet problems[J],Nonlinear Anal.2004,57(3) :473-484. [7]Lin Changshou;Tso Kaising,On regular solutions of second order degenerate elliptic-parabolic equations[J].Comm.P.D.E.,1990,15(9):1329-1360. [8]Y.S.Choi,A.C.Lazer,P.J.McKenna,On a singular quasilinear anisotropic elliptic boundary value problem[J].Trans.A.M.S.,1995,347(7) :2633-2641. [9]Y.S.Choi,and P.J.McKenna,A singular quasilinear anisotropic elliptic boundary value problem II[J].Trans.A.M.S.,1998,350(8) :2925-2937. [10] F.St.Cirstea,and V.D.Radulescu,Existence implies uniqueness for a class of singular anisotropic elliptic boundary-value problems[J].Mathematical Method in the Applied Sciences,2001,24(11) :771-779. [11] 徐中海.一类含有梯度项的塑性流体数学模型正解的存在性及正则性[J].厦门大学学报:自然科学版,2013,52(1):1-4. [12] 刘生全,徐中海.粘性系数依赖于密度的一维粘性Navier-Stokes方程组解的全局存在性[J].东北电力大学学报,2014,34(2):87-91. A Fully Proofs of Nature of Solutions for a Second Order Ordinary Differential Equation Initial Value Problem ZHANG Da-peng1,XUE Wen2,ZHU Xiu-li1,XU Zhong-hai1,2 (1.Science College,Northeast Dianli University,Jilin Jilin 132012;2.Editorial Department,Northeast Dianli University,Jilin Jilin 132012) In the Appendix B of [1],the classical solution properties of a class of second order ordinary differential equation initial value problems are researched,and gives the corresponding theoretical proofs.The author thinks that there are some omissions in the proofs.By the proof’s basic role in [1],this paper gives the corresponding complete proofs. Second order ordinary differential equation;Initial value problem;Bounded 2016-04-12 吉林省自然科学基金(20150101002JC) 张大鹏(1983-),男,吉林省吉林市人,东北电力大学理学院在读硕士研究生,主要研究方向:数学应用. 1005-2992(2016)04-0096-03 O175.1 A
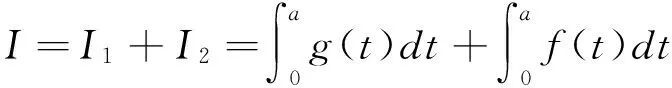
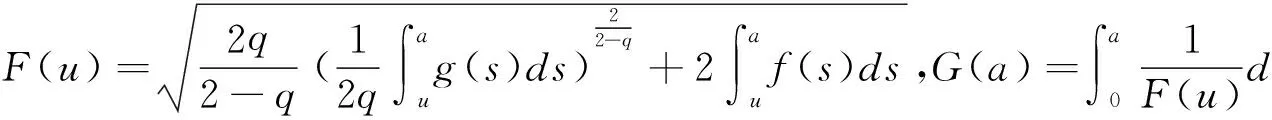
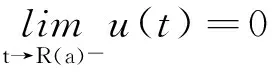
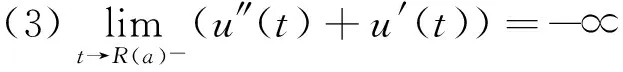
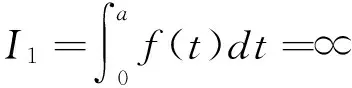
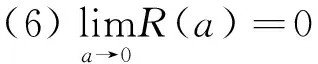
1 引理B的一个完整证明
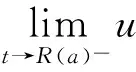
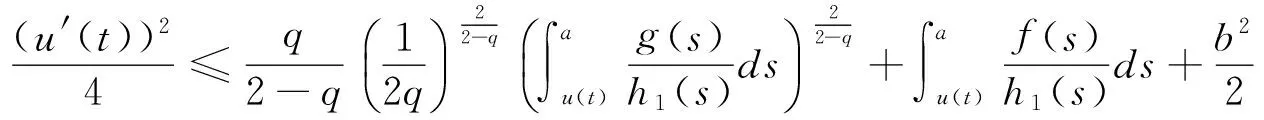
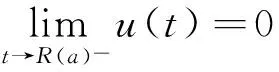
2 几点说明
———理学院

