管式电除尘器内部细颗粒流动数值模拟

郑建祥，吕辛桐，唐　晨，康文瑶，周天鹤

(东北电力大学 能源与动力工程学院，吉林 吉林 132012)



管式电除尘器内部细颗粒流动数值模拟

郑建祥，吕辛桐，唐晨，康文瑶，周天鹤

(东北电力大学 能源与动力工程学院，吉林 吉林 132012)

为了进一步探究电除尘器内颗粒的流动对除尘效率的重大影响，采用k-ε湍流模型和离散相模型对电除尘器内部颗粒流动进行了多组工况的数值模拟。利用用户自定义函数(UDF)编辑电场荷电方程并建立电场受力模型，简化了模拟流程，并优化了模拟数据。通过流场与电场的耦合计算，研究并分析了不同进出口风速对、颗粒直径以及电压等因素对除尘效率的影响。结果表明：电压和粒径恒定时，随着进口风速增加，颗粒滞留时间减少，荷电量不足，颗粒偏移运动越加不明显，除尘效率降低。当电压和进口风速恒定时，由于粒径的平方与颗粒荷电量成正比，所以粒径越大，颗粒荷电量越大，除尘效率变化越高。在进口风速与粒径恒定时，荷电量与电晕电压成正比，电压越大，荷电量越大颗粒受电场力而向收尘壁运动越明显，从而收尘除尘效率明显增加。

除尘效率；颗粒；风速；电压；偏移

近些年来，全球范围内的雾霾现象越来越严重，它对社会发展、环境保护和人们日常生活以及健康等诸多方面有着极其不利的影响。究其来源主要是大型工厂烟气、灰尘中的细颗粒。国内外研究员们对于如何提高大型工厂中电除尘器除尘效率的课题已经有了比较深入的研究和认识。龙正伟[1]针对静电除尘器的模拟建立了三维物理模型，更好的分析电除尘器内部流场分布以及颗粒电荷特性与除尘效率的关系；朱继保[2]研究了在如何控制二次扬尘、优化电源、复合除尘技术等方面因素来提升除尘效率；Talaie等[3]人提出了一种能够计算出电晕极板的半径增加率和电晕边缘的离子密度电场计算模型，同时还指出了Choi[4]计算网格太细，没有基于基本的物理事实等不足之处。Ivancsya[5]研究了静电除尘器内多种分散尘粒的特性，采用了多相颗粒的模型，并与单种颗粒的计算结果进行了比较。

本文利用GAMBIT建模并进行网格划分，然后将模型导入FLUENT，针对风速、颗粒直径、电压等因素进行了多组工况的数值模拟。其中，气相流场采用了k-ε湍流模型，颗粒相采用DPM模型。利用UDF编辑电场荷电方程，并建立了电场受力模型。UDF编辑成的电场受力模型不仅便捷了模拟流程，而且优化了模拟数据。针对电场与流场的耦合计算结果，对比分析三种进气口风速，三种颗粒粒径以及三种电压下研究颗粒流动变化规律，以及这些规律对除尘效率的影响。

1　数学模型与数值模拟方法

1.1流场模型

在电除尘器中，除尘是一个气固两相流动并相互作用的过程，气体的流动带着悬浮着的颗粒运动。湍流流动可以通过气体质量守恒方程和气体动量守恒方程来求解。

气体质量守恒方程：

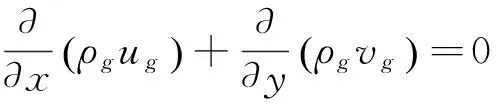
(1)

气体动量守恒方程：

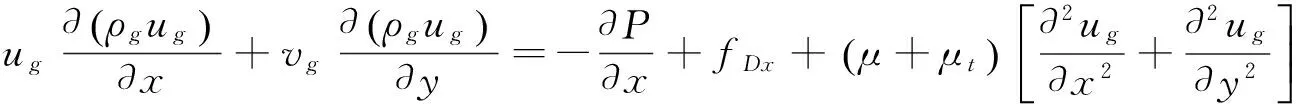
(2)

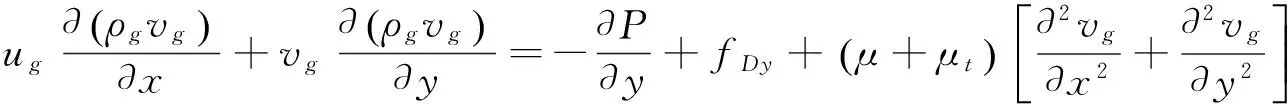
(3)

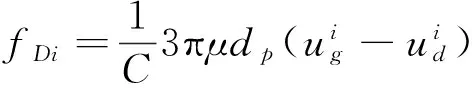
1.2电场模型

电除尘器中颗粒荷电方式一般有两种，一种是扩散荷电(主要针对小于1 μm的颗粒)；另一种是电场荷电(主要作用于大于1 μm的颗粒)。本次主要模拟颗粒粒径为1 μm，5 μm，10 μm这3种工况。为了简化模拟过程，忽略颗粒扩散荷电的影响。

由于所选择的物理模型中没有电场力这个物理量，所以建立电场受力模型一般有两种方法。一种是利用FLUENT中隐藏模型中的磁流体模型(MHD)建立电场模型，另一种是UDF编辑电场模型。第一种方法使用复杂，只能模拟简单低压匀电场，不能体现颗粒受电场力的具体变化，局限性较大；第二种UDF编辑的方法是将作用到颗粒上的电场力以电场荷电方程的形式呈现，不仅能调节颗粒在空间电荷区内部的所受电场力大小，不再有电压大小的限制，而且还能体现出不同电场荷电方程中颗粒荷电受力情况。这也使得模拟结果更加接近实验数据，符合事实。利用用户自定义函数(UDF)编辑电场荷电方程，并建立电场模型的这种方法优化便捷了模拟结果。构建电场模型所需要用到电场荷电方程：

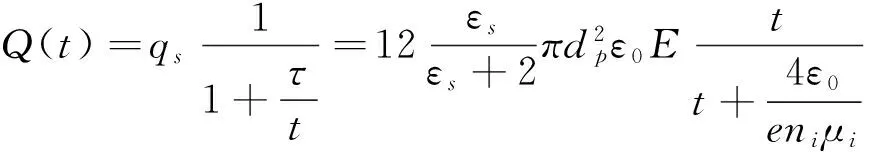
(4)

式中：qs为颗粒饱和电量，C；εs为颗粒的相对介电常数；dp为颗粒粒径，μm；E为载入电压，V；t为荷电时间，s； μi为离子迁移率，m2/Vs。

1.3颗粒运动模型

电除尘器中的颗粒之间也存在着力的平衡，并且烟气中颗粒的体积分数不足10%，完全符合DPM模型的使用条件。在模型中为了更真实的模拟这一情况，通过利用积分拉式坐标下的颗粒作用力微分方程来求解离散相颗粒的轨道。颗粒的作用力平衡方程(颗粒惯性=作用在颗粒上的各种力)在笛卡尔坐标系下[6-9]的行驶(x方向)为

(5)

其中：FD(u-up)为颗粒的单位质量曳力，对于亚观尺度(直径在1 μ到10 μ之间)颗粒，Stokes曳力公式是适用的。这种情况下，FD定义为

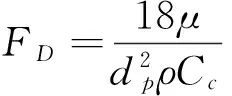
(6)

其中：dp为颗粒粒径，m；ρ为颗粒骨架密度，kg/m3；Cc为Stokes曳力公式的Cunninghanm修正(考虑稀薄气体力学的颗粒壁面速度滑移的修正)。

2　数学物理模型的边界条件和网格划分

在电除尘器中，当电压超过起晕电压时，内部空气被电离形成大量颗粒自由电子[9]。在电晕电压的作用下，电子被驱赶出空间电荷区。自由电子的无规则运动碰撞到烟气中的粉尘颗粒，使得颗粒荷电。在电场中，随着时间和电压的增加颗粒荷电量增加，从而导致带有负电荷的颗粒向收尘壁(正极)的偏移运动更加明显剧烈，直到颗粒抵达收尘壁并且被捕集。电除尘器详细边界条件，参考表1所示。

表1 边界条件

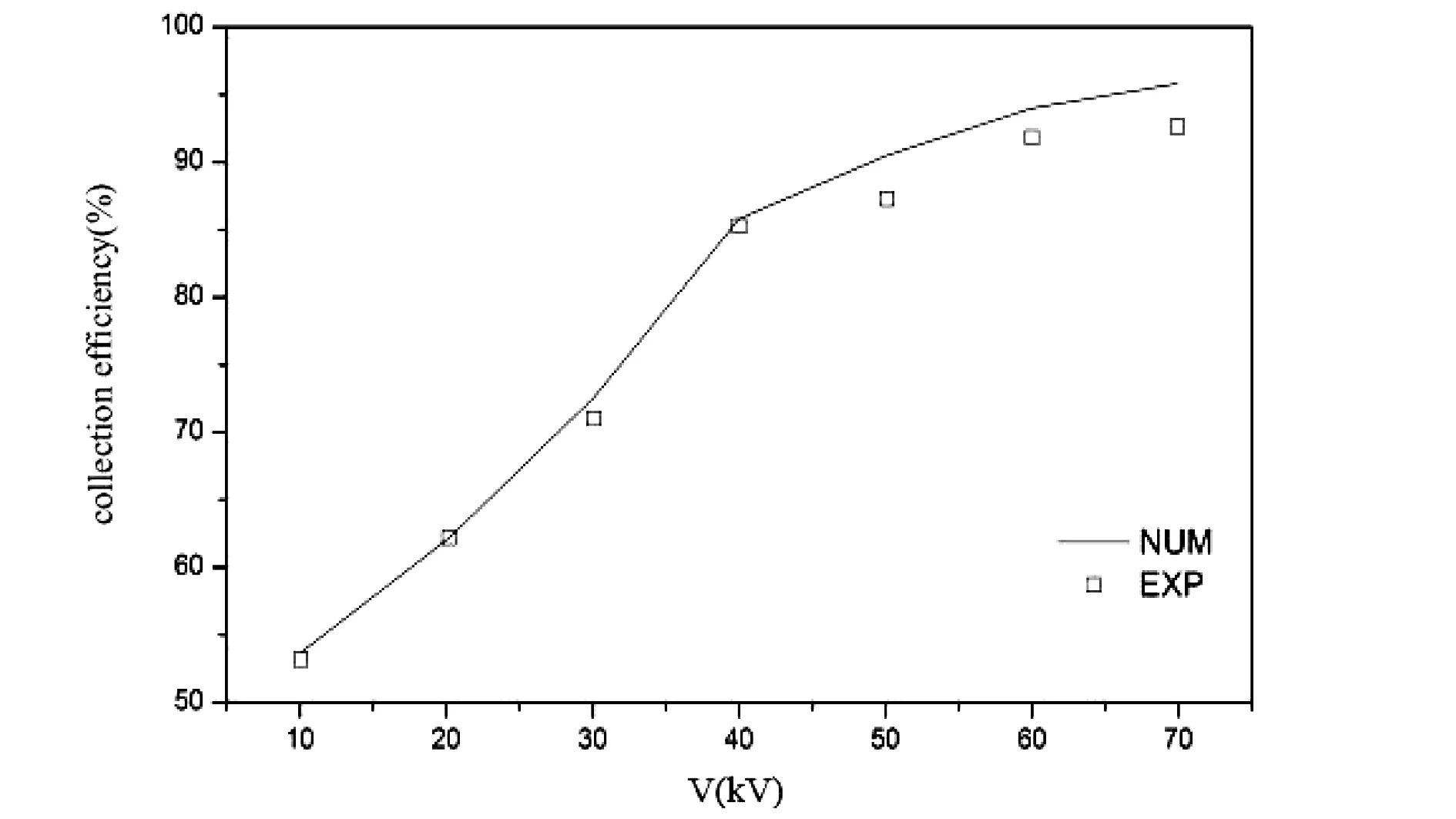
图1　模拟数据与实验数据比对

本文模拟的是管式静电除尘器，为了便于数值模拟的计算以及模型的对称性，所以只选取了一半的模型来划分网格，网格数目为460×160。

3　数值模拟结果及分析

3.1湍流模型验证

为了验证数值模拟的模型的正确性，将数值模拟模型中的一些可变参数按照Zakariya Al-Hamouz的实验数据[10]带入计算，结果如图1所示。从图1中可以看出,数值模拟的计算结果与实验操作后得出的结果还是比较相近的，基本上可以符合实验结果。同时，数值模拟的计算结果要略高于实验结果。那是由于现实中颗粒形状是不规则，文中为了便于模拟，把颗粒只假设成球形颗粒一种，从而增加了一些不规则形状的颗粒质量增加，半径变大，使颗粒受到的电场力增加除尘效率变高。虽然分析结果略高，不过还在标定的范围内。

3.2不同的进口风速对除尘器集尘效果的影响

对于电除尘器来说，进气口风速大小是影响除尘效率高低的重要因素之一。进风口对除尘效率的影响十分明显,本文分别模拟出不同进口风速对除尘效率的影响，如图2所示。

从图2(a)中可以看出，在进气口风速为0.3 m/s时的除尘效率随着颗粒粒径的增加而增加。这是由于颗粒悬浮于烟气中，烟气带动着颗粒运动。所以，进口风速的大小决定着颗粒在除尘器内部滞留时间的长短。颗粒如果在电场中滞留时间增加，那么颗粒与自由电子碰撞的时间增加，荷电量增加，收到电场力作用变大，颗粒偏移运动程度增加，更多的粉尘颗粒吸附到除尘壁上，从而导致除尘效率增加，反之亦然。在图2(a)中，进口速度为0.7 m/s和1.2 m/s时的除尘效率变化趋势与进口速度0.3 m/s的相同，但是在相同粒径下风速为0.3 m/s的除尘效率明显高于其他两条曲线的除尘效率。

粒径为1 μm-5 μm时，随着风速的减小，除尘效率在增加。风速较低时，除尘效率上升的趋势要高于风速较高的，尽管除尘效率上升的较为平缓。当粒径5 μm-10 μm时，与之前小粒径变化基本相同；唯一不同的是在粒径大于5 μm时，除尘效率上升的幅度较小粒径增长幅度增大了许多。在图2(b)、图2(c)中，变化趋势与图2(a)相同，只是随着电晕电压的增大，除尘效率也在增大，在电压为70 kV时，进口风速为0.3 m/s，粒径大于5 μm的工况下，除尘效率接近100%。

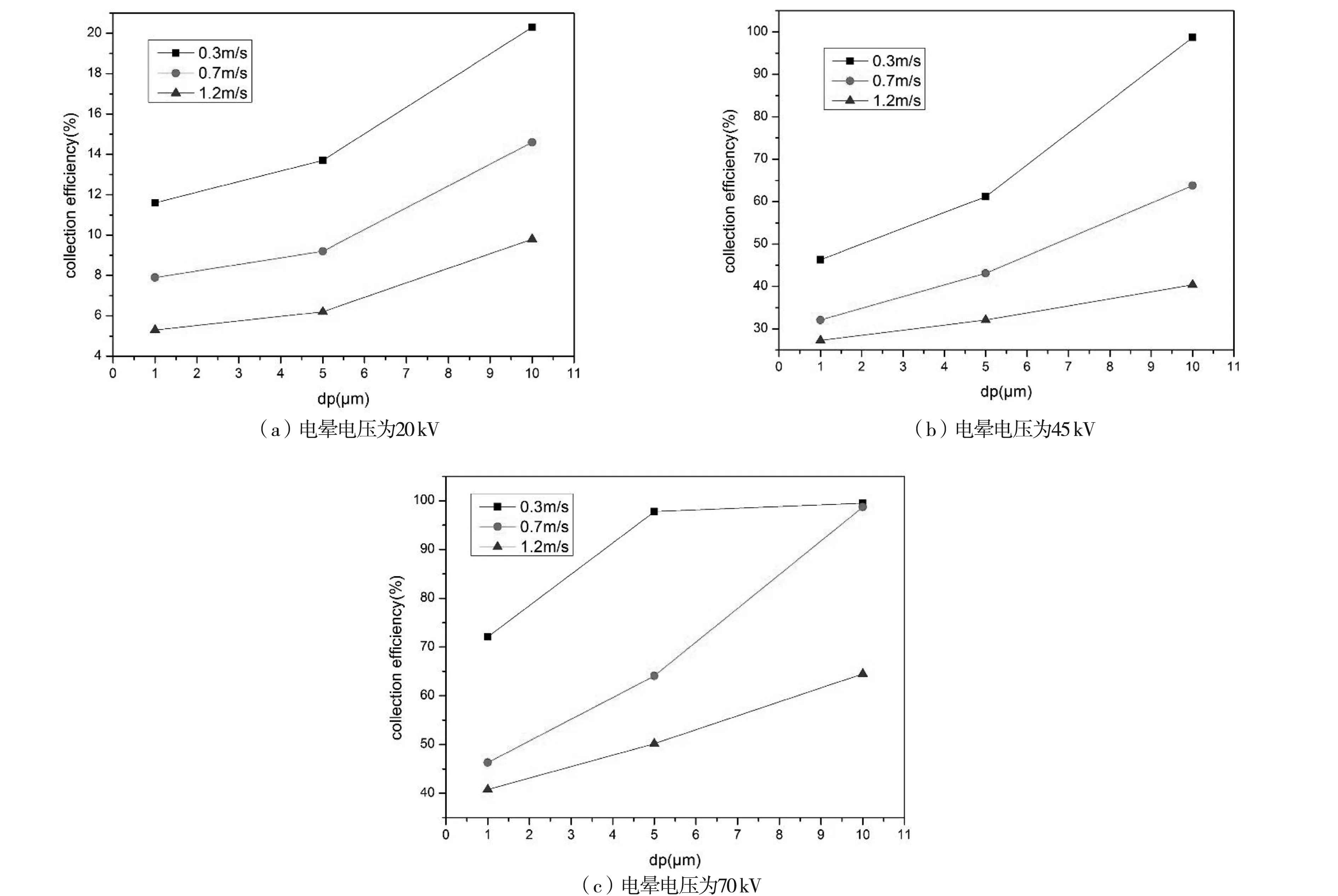
图2　不同进口风速对除尘效率的影响

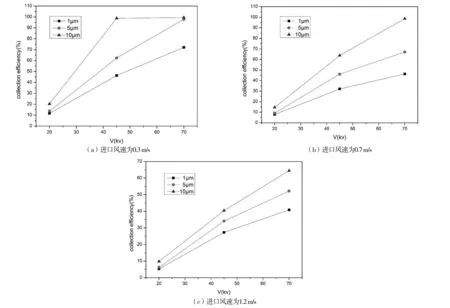
图3　不同粒径对除尘效率的影响

3.3不同的颗粒粒径对除尘器集尘效果的影响

电除尘器中颗粒粒径的大小对除尘器的除尘效率高低有着直接影响，下文描绘了三种不同粒径对除尘效率的影响，如图3所示。

在图3(a)中，进口风速为0.3 m/s，粒径为10 μm时，随着电晕电压增大，除尘效率呈现出非线性增加。在粒径为5 μm和1 μm时，除尘效率变化相同。对比三条曲线，明显可以看出，在电场中大粒径颗粒的除尘效率要高于小粒径的。这是由于在电压和进口风速恒定的工况下，颗粒荷电量与粒径大小成正比，粒径越大荷电量越大，颗粒受到的电场力越大。颗粒偏移运动越明显，收尘壁会捕集到的粉尘颗粒越多，除尘效率就越高，反之同理。从三条曲线随着电压增加的变化中还可以看出，在电压较小的工况下，随着电压增加，除尘效率增加的幅度较大。颗粒粒径越大，这种增幅的变化越大，除尘效率增长越高。当电压增加到较高时，这种增加的幅度会越来越小。这种变化趋势在粒径越小的颗粒比较明显,图3(b)与图3(c)的变化趋势和图3(a)基本相同。

3.4不同的电晕电压对除尘器集尘效果的影响

电晕电压是电除尘器除尘的源动力。不同的电晕电压，导致颗粒向X轴偏移的程度也不同,偏移程度影响了除尘效率的高低。

图4　颗粒向X轴偏移运动轨迹

在颗粒粒径为5 μm，进口风速为0.3 m/s的工况下，描绘了三种电压下的颗粒运动轨迹云图，如图4所示。从图4中可以看出，在电压为20 kV时颗粒的偏移轨迹变化较小，直到颗粒到达出口时的偏移距离不到100 mm;而在电压为45 kV时，颗粒的偏移距离超过了100 mm，可见颗粒偏运动加剧了;在电压为70 kV时，颗粒没能运动至出口处就完全被收尘壁捕集了。在进口风速与颗粒粒径恒定时，随着电晕电压的增加，电场中产生更多的自由电子。当自由电子与粉尘颗多次粒碰撞后，粉尘颗粒的荷电量明显增加，直到饱和。颗粒荷电量越大，受电场力作用越大。从而使得粉尘颗粒与向收尘壁运动的偏移量增加，收尘壁捕集更多的粉尘颗粒，最后除尘效率增加。

4　结　　论

本文建立了一个管式电除尘器的物理模型来模拟颗粒流动。通过流场与电场耦合，再模拟计算出三种不同进口风速，粒径以及电晕电压等因素对除尘效率的影响，得到如下结论。

(1)本文利用UDF编辑方程并建立电场模型，简化了模拟流程，避免了MHD模型的应用。此模型还可以模拟高电压的工况，增加了电压模拟范围，消除了MHD模型的局限性，也优化了模拟数据。在模型验证中，证明了模拟数据符合实验数据。

(2)在电晕电压和颗粒粒径恒定时，随着进气口速度的减小，粉尘颗粒滞留时间增加，荷电量增加，颗粒受到电场力作用而向收尘壁偏移运动更加明显。最终,收尘壁捕集到的粉尘颗粒增加，除尘效率增加。

(3)电晕电压和进口风速恒定时，随着颗粒粒径的增大，颗粒荷电量增加，受电场力作用向收尘壁运动更加剧烈。更多的粉尘颗粒吸附到收尘壁，电除尘器除尘效率增加，并呈现出非线性的增加的趋势。粉尘颗粒粒径越大，除尘效率增加的趋势越明显。

(4)在颗粒粒径和进口风速恒定时，电晕电压越大，粉尘颗粒与电子碰撞次数越多，颗粒荷电量越大，直至饱和。相对的颗粒向收尘壁偏移的距离越大，收尘壁捕集粉尘颗粒越多，除尘效率增加。

[1]龙正伟，冯壮波，姚强.静电除尘器数值模拟[J].化工学报，2012，63(11)：3394-3401.

[2]朱继保.细颗粒物的电收集技术研究[D].杭州：浙江大学，2010，11-17.

[3]Talaie M R，Taheri M，Fathikaljahi J.A new method to evaluate the voltage-current characteristics applicable for a single-stage electrostatic precipitator [J].Journal of Electrostatics，2001，53(3)：221-233.

[4]Choi B S，Fletcher C A J.Computation of particle transport in an electrostatic precipitator [J].Journal of Electrostatics，1997，40(41)：413-430.

[5]Iváncsy T，Suda J M.Behavior of poly-disperse dust in electrostatic precipitators [J].Journal of Electrostatics，2005，63(10)：923-927.

[6]Jen-ShihChang，Francisco Pontiga.Pierre Atten，Antonio Castellanos.Hysteresis Effect of Corona Discharge in a Narrow Coaxial Wire-Pipe Discharge Tube with Gas Flow[J].IEEE Transcations on Industry Applications,1996，32(6)：1250-1256.

[7]Z.Mzaur，R.Campos-Amezcua.Numerical 3D simulation of the erosion due to solid particle impact in the main stop valve of steam turbine[J].Applied Thermal Engineering，2004，24(13)：1877-1891.

[8]闻建龙，陈汇龙，王军锋，陈松山.荷电两相流动颗粒运动微分方程的建立[J].排灌机械，2003，21(4)：43-45.

[9]李少华，宋阳，王铁营，等.下时风袋式除尘器内部流场的数值模拟[J].东北电力大学学报，2015,35(1)：12-17.

[10] 周涛.黏性颗粒聚团流态化及应用[M].北京：化学工业出版社，2008，9.

[11] Zakariya Al-Hamouz，Amer El-Hamouz，Nabil Abuzaid，Simulation and experimental studies of corona power loss in a dust loaded wire-duct electrostatic precipitator[J].Advanced Powder Technology，2011(22)：706-714.

Tube Type Electric Precipitator Internal Flow Numerical Simulation of Fine Particles

ZHENG Jian-xiang，LV Xin-tong，TANG Chen，KANG Wen-yao，ZHOU Tian-he

(Energy Resource and Power Engineering College，Northeast Dianli University，Jilin Jilin 132012)

In order to further explore the influence of particle flow on the dust removal efficiency，the numerical simulation of the internal particle flow in electrostatic precipitator is carried out by using the turbulent model and discrete phase model.By using the user defined function (UDF) to edit the electric field charge equation and to establish the force model of the electric field，the simulation process is simplified，and the simulation data is optimized.Through the coupling calculation of the flow field and the electric field，the influence of different inlet and outlet velocity，particle diameter and voltage on the dust removal efficiency is studied and analyzed.The results show that when the voltage and the particle size fixed，increase of inlet velocity and decrease of the particles residence time lead to insufficient charge.Particle migration movement has become increasingly obvious，and dust removal efficiency is lower than before.Because the square of the particle size is proportional to the charge quantity，so the bigger the particle size is，the bigger the charge quantity is，and the higher the dust removal efficiency is.When the inlet velocity and particle size is constant，the voltage is greater，the greater the charge.Electric force of particles to dust wall motion is more obvious，so dust removal efficiency increased significantly.

Dust removal efficiency；Particle；velocity；Voltage；Deviation

2016-04-12

郑建祥(1977-)，男，福建省建瓯市人，东北电力大学能源与动力工程学院副教授，博士，主要研究方向：气固两相流动.

1005-2992(2016)04-0067-06

X513

A