病态线性方程组的并行迭代求解

黄丽嫦，林 结，黄 润

（1.佛山职业技术学院基础教学部，广东佛山528137；2.佛山职业技术学院电子信息系，广东佛山528137）

病态线性方程组的并行迭代求解

黄丽嫦1，林 结1，黄 润2

（1.佛山职业技术学院基础教学部，广东佛山528137；2.佛山职业技术学院电子信息系，广东佛山528137）

分析了病态线性方程组的相关概念及判别方法，给出了一种病态线性方程组并行迭代的求解算法。算法首先对病态线性方程组的系数矩阵进行严格对角占优预处理，在此基础上，用并行的Jacobi迭代法进行多步迭代求解。新算法易于在多核架构的微机中实现，且数值实验也验证了算法具有良好的收敛性和并行性。

病态线性方程组；并行计算；雅可比迭代法

线性代数是数值计算方法的基础，许多科学研究和工程技术等实际问题的求解最终都可转化为线性代数问题来处理，如计算插值函数与拟合函数，最小二乘数据拟合，构造求解微分方程的差分格式等［1-2］。当方程组的系数行列式不为零时，根据克莱姆（Cramer）法则便可以求出方程组的惟一解，然而这一理论完善的方法在高阶线性方程组中因计算量庞大而变得难以应用［3］，因此如何建立有效而实用的线性方程组求解方法，具有重要的现实意义。目前，线性方程组的求解方法大致可以分为两类：直接法和迭代法［4-5］。直接法是指假设在没有舍入误差的条件下，能在预定的运算次数内求得精确解的方法，由于在实际计算过程中总存在误差，因此直接法存在数值计算的稳定性问题。而迭代法则是从解的某个近似值出发，通过构造一个无穷序列去逼近精确解的方法，迭代法因为具有方法简单且易于实现的优点而更具应用价值。本文在多核架构的微机中，基于雅可比（Jacobi）迭代法研究了病态线性方程组的并行求解问题，并设计实现相应的迭代求解算法，数值实验也验证了算法具有良好的收敛性和并行性。

1　病态线性方程组的判别方法

1.1线性方程组的病态问题

考虑n阶非奇异线性方程组

其中，A=（aij）∈Rn×n且det（A）≠0，x=（x1，x2，…，xn）∈Rn，b=（b1，b2，…，bn）∈Rn，若式（1）中的系数矩阵A和右端项b的微小扰动引起了解x的巨大变化，则称该线性方程组为病态线性方程组，否则称其为良性线性方程组。

线性方程组的病态性强弱程度一般可用下式（2）所示的条件数进行定量描述［6］

1.2病态方程组的判别方法

利用式（2）对线性方程组的病态性进行描述，其主要困难在于对‖A-1‖V的计算，当然，可以通过求解方程组Ayi=I（i=1，2，…，n，I为n阶单位矩阵）而得到A-1=［y1，y2，…，yn］，然后再求出‖A-1‖V，然而这样所需的计算量却不低于求解x的计算量，因此有必要引入简便而实用的线性方程组条件数估计方法。事实上，对于式（1）所示的非奇异线性方程组而言，由于det（A）≠0，则方程组有惟一解，即

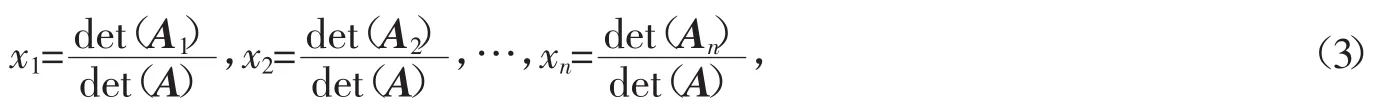
其中，Ai（i=1，2，…，n）是把系数矩阵A中第i列元素用方程组右端项b代替后所得的n阶矩阵。若式（1）中某些元素的扰动使得det（A）、det（Ai）的增量分别为ΔT和ΔTi，当（det（A）+ΔT）≠0时，则此时方程组对应的解为

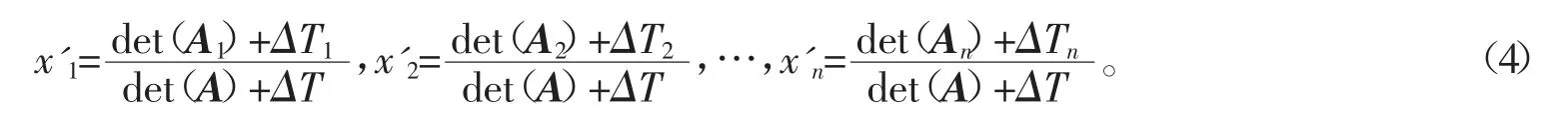
设系数矩阵A=［a1，a2，…，an］，ai∈Rn，当向量组a1，a2，…，an的线性相关程度较小时，|det（A）|将取较大的数值，所以有|det（A）|>>|det（Ai）|，从而有xi≈x'i，即扰动对方程组的解的影响较小，故此时的线性方程组是良态的；反之，当向量组a1，a2，…，an的线性相关程度较大时，|det（A）|将取较小的数值，此时扰动对方程组的解的影响较大，即线性方程组是病态的。

从上述分析可知，通过计算系数矩阵A的行列式便可判断方程组的病态性，这里引入如下引理。

引理1［7］对于非奇异线性方程组Ax=b而言，设det（A）=Σ（-1）ta1p1a2p2…anpnK=max（a1p1a2p2…anpn），若K>>|det（A）|，则方程组是病态的。

引理1中，p1，p2，…，pn为系数矩阵A的元素的列标号，t为排列p1，p2，…，pn的逆序数，Σ表示对n个数的所有排列p1，p2，…，pn取和［8］。

2　病态线性方程组的并行迭代求解算法设计

2.1线性方程组的并行迭代求解原理

利用迭代法求解方程组，就是构造一个无限的向量序列，使它的极限是方程组的解向量。为了更好地发挥目前主流的微机多核计算功能，本文拟采用具有良好并发性能的Jacobi迭代法来研究病态线性方程组的求解问题。

由于迭代法不能通过有限次算术运算求得方程组的精确解，因此，收敛性与精度控制是迭代法的核心问题。对于Jacobi迭代法，有如下引理。

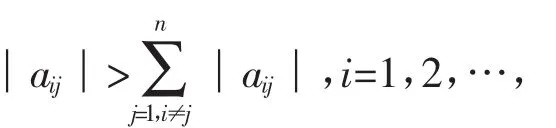
（1）A为非奇异；

（2）Jacobi迭代法收敛。

为确保病态线性方程组Ax=b的Jacobi迭代收敛，根据引理2中的收敛性质，可对病态线性方程组的系数矩阵A进行如下分解

然后在方程组左右两边加上一个对角矩阵M，有

对式（6）进行移项及整理，有

从而得到如下的迭代形式

于是，相应的Jacobi迭代为

2.2算法的设计及实现

从式（9）可知，迭代表达式x1（k+1），x2（k+1），…，xn（k+1）之间没有关联，可将它们平均分布在CPU中的各个核中计算。因此，可设计如下病态线性方程组的Jacobi并行迭代算法。

算法名称：病态线性方程组的Jacobi并行迭代算法。

输入：病态线性方程组的矩阵系数An×n，常数向量bn×1，迭代精度e，初始解向量xn×1；

输出：病态线性方程组的解向量xn×1。

算法描述：（设CPU的核数为P）

（1）初始化及预处理。

1）从系数矩阵A中分离出P，Q矩阵，其中P=aii｛｝，Q=aij｛ ｝，i≠j，1≤i，j≤n；

（2）并行迭代计算过程。

do｛

2）各计算核完成当前迭代计算后，将自己所计算分量的新值广播到所有计算核中；

｝while（diff＞e）

（3）输出解向量xn×1。

3　算法的性能测试

为了检验上述设计算法的有效性，本文在Intel Xeon E54504核3.0 GHz CPU（每个计算核的一级缓存各由32 KB数据缓存和32 KB指令缓存组成，二级缓存容量为12 MB，）、KingSton DDR3 1 333 MHZ 4 GB内存及Red Hat Enterprise Linux 6.1操作系统的环境中进行了相关的数值试验，程序采用OpenMP和C++语言进行编写。

分别用Jacobi迭代法和本文改进的算法对不同阶数的Hilbert经典病态问题进行试验，其中，Hilbert病态问题的系数矩阵如下式（10）所示［10］

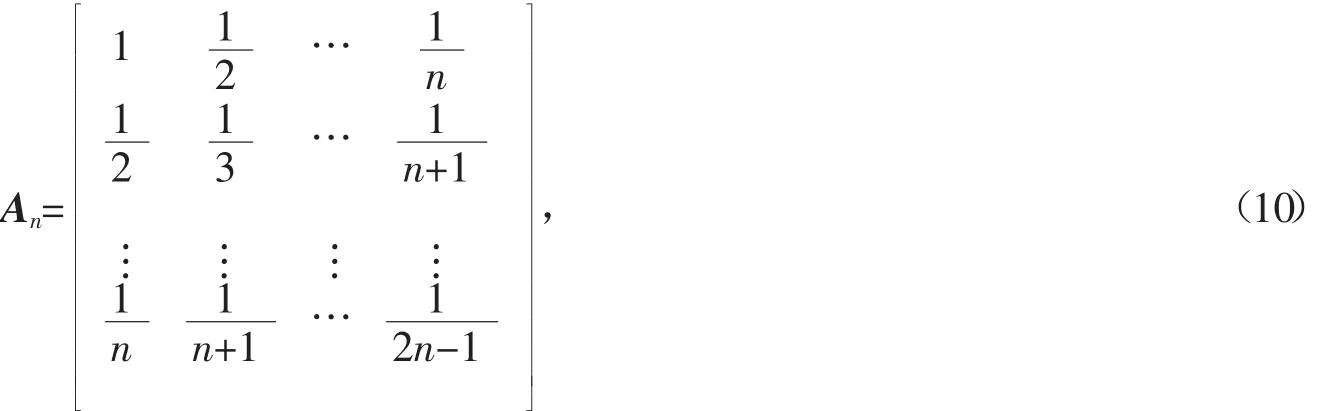
而b=An［1 1…1］T，在计算精度e=1×10-12的条件下，得到如表1所示的计算结果。

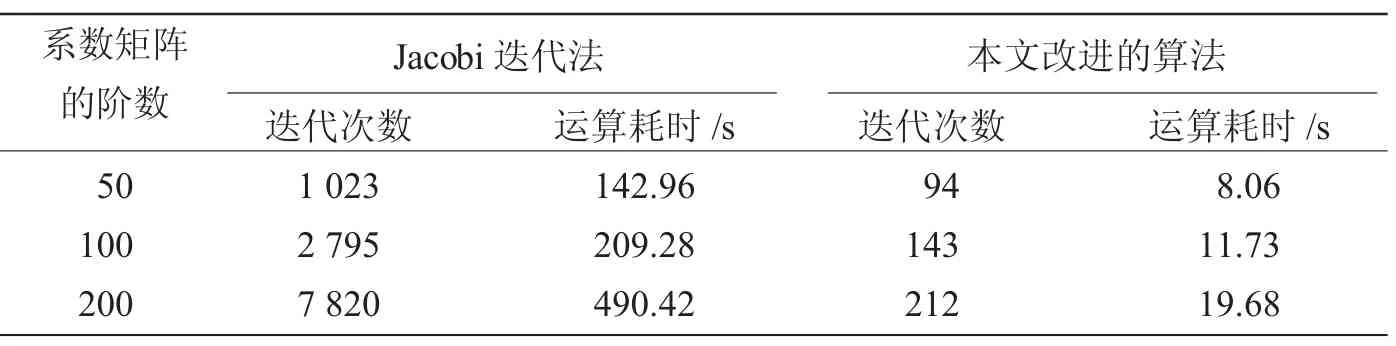
表1　Jacobi迭代法与本文改进算法的计算性能比较

实验数据表明，在同样计算精度的条件下，由于加入有效的预处理，因此本文的改进算法在计算效能上得到了有效改善。

4　结语

本文介绍了病态线性方程组的有关概念以及判别方法，在基于多核架构的微机中提出了求解病态线性方程组的并行迭代算法，由数值试验得知，算法的改善效果是明显的。

［1］丁丽娟，程杞元.数值计算方法［M］.2版.北京：北京理工大学出版社，2005：12-74.

［2］李大明.数值线性代数［M］.北京：清华大学出版社，2010：1-36.

［3］吕全义.线性代数［M］.北京：清华大学出版社，2015：1-21.

［4］陈长军.数值计算理论与实现［M］.武汉：华中科技大学出版社，2014：32-66.

［5］沈艳.高等数值计算［M］.北京：清华大学出版社，2014：20-60.

［6］徐树方.矩阵计算的理论与方法［M］.北京：北京大学出版社，1995：54-75.

［7］郑孝勇，张东俊.病态线性方程组的判定方法［J］.数学的实践与认识，2006，36（9）：166-169.

［8］居余马.线性代数简明教程［M］.北京：清华大学出版社，2004：1-95.

［9］李庆扬.数值计算原理［M］.北京：清华大学出版社，2000：140-241.

［10］林胜良.病态线性方程组解法研究［D］.杭州：浙江大学，2005：51-54.

【责任编辑：王桂珍foshanwgzh@163.com】

Parallel iterative method for solving ill-conditioned linear equations

HUANGLi-chang1，LINJie1，HUANGRun2

（1.Department ofBasic Teaching，Foshan Polytechnic，Foshan 528137，China；2.Department ofElectronic Information，Foshan Polytechnic，Foshan 528137，China）

This paper analyzes the concepts and discriminatimg methods of ill-conditioned linear equations，presents a parallel iterative algorithm.The pretreatment algorithm based on ill conditioned coefficient matrix of the linear equations is strictlydiagonallydominant，based on multi step iterative method for solvingthe equations after pretreatment with parallel Jacobi iterative method.The new algorithm is easy to implement on computer multi-core architecture，and the numerical experiments show that the algorithm has good convergence and parallelism.

ill-conditioned linear equations；parallel computation；Jacobi iteration

O241.6

A

1008-0171（2016）04-0013-05

2016-01-20

佛山职业技术学院校级科研基金资助项目（KY2013Y07）

黄丽嫦（1962-），女，广东中山人，佛山职业技术学院讲师。