具有逆断面的正则半群上的同余

冯莹莹，商 宇

（1.佛山科学技术学院数学与大数据学院，广东佛山528000；2.普洱学院数学与统计学院，云南普洱665000）

具有逆断面的正则半群上的同余

冯莹莹1，商 宇2

（1.佛山科学技术学院数学与大数据学院，广东佛山528000；2.普洱学院数学与统计学院，云南普洱665000）

给出具有逆断面的正则半群上同余的3种刻画方式：IR，ΛL和LR。

逆断面；正则半群；同余；刻画

自从Blyth和McFadden在1982年提出具有逆断面的正则半群的概念后，这类半群因具有相对集中的逆子半群的结构而备受关注。不少作者先后研究了这种半群，并得到了丰硕的成果。Saito于1982年给出了这类半群的结构定理：具有逆断面的正则半群S由3个构件I、S°和Λ组成，其中S°是S的逆子半群，I、Λ分别为左正则带、右正则带。此外，左逆子半群L、右逆子半群R也是我们比较感兴趣的结构子半群。在这类半群的同余的研究问题上，汪立民［1］首创性地给出了具有Q-逆断面的正则半群上同余的刻画：具有Q－逆断面S°的正则半群S上的同余可由3个结构构件I、S°和Λ上的同余所作成的同余三元组确定。利用这种同余刻画方式，可以研究S上的同余格。随后，唐西林和汪立民［2］对这种方法进行推广，刻画了具有逆断面的正则半群上的同余，并在文献［3］中研究了此类半群的同余格上T、Tr、Tl、U、V这5个等价关系。本文则从另一个角度给出具有逆断面的正则半群上同余的另外3种刻画方式，它们分别由结构构件I和R，Λ和L，以及L和R上的同余所作成的同余对给出。

本文沿用文献［4-5］中的记号。设S是半群，记S的幂等元集为E（S），S上的同余格为C（S）。记为a的逆元集。设γ是S上的一个关系，由γ生成的同余记为γ*。

设S是正则半群，S°是S的逆子半群，如果S°含有且只含有S的每个元的一个逆元，即对任意x∈，则称S°为S的逆断面。x在S°中惟一的逆元记作x°，因此记（x°）-1= x°°，则对任意x∈S，x°°°=x°。在此作一个约定，下文中所指的半群S，如无特别声明，均表示具有逆断面S°的正则半群。下面列举这类半群的一些基本性质。

结论1设S是具有S°逆断面的正则半群，则

（1）（∀x，y∈S）（xy）°=y°（xyy°）°=（x°xy）°x°=y°（x°xyy°）°x°。

（2）（∀x，y∈S）（xy°）°=y°°x°。

（3）S是纯正的当且仅当（∀x，y∈S）（xy）°=y°x°［6］。

文献［2］中针对具有逆断面S°的正则半群的以I、S°、Λ为构件的结构，用同余三元组给出具有逆断面的正则半群上同余的刻画。我们首先把其中的符号和结论引述如下。设S是具有逆断面S°的正则半群，ρ是S上的同余，记

结论2设S是具有逆断面S°的正则半群。若xρy，则x°ρ°y°［2］。

如果I上的同余τ满足

则称τ是I上的正规同余。Λ上的正规同余可以对偶地定义。

设τI、τΛ分别为I、Λ上的同余，π为S°上的同余，如果三元组（τI，π，τΛ）满足

则称（τI，π，τΛ）为S上的同余三元组。定义S上的关系ρ（τI，π，τΛ）为

结论3设S是具有逆断面的正则半群，对S上的每一同余三元组（τI，π，τΛ），ρ（τI，π，τΛ）是使在I、S°、Λ上的限制分别为τI、π、τΛ的惟一同余。反之，S上的每一同余均可如此构造［2］。

1　同余的刻画和同余格

Saito在文献［8］中以I、R为构件得到具有逆断面S°的正则半群S的结构定理。在本节中，笔者基于这个结构定理，引入I、R上同余相容的条件，以及用I、R上的同余作成同余对，给出S上相应的同余的刻画。首先，考虑S上的同余在子半群R和L上的限制。对ρ∈C（S），分别规定R、L上的关系ρR、ρL为

在引理1的观点下，可以认为ρR、ρL是ρ分别在R、L上的限制。

引理2设τ∈C（R），a，b∈R且a τ b，则a°τ b°。

证明 因为R是具有逆断面S°的正则半群，τ∈C（R），a τ b，由引理1知，a°τ b°。

下面定义R和L上的正规同余。设S为半群，T为S的子半群，ξ∈C（T），如果存在ρ∈C（S）使得则称ξ可扩张到S上。

定义1设S是具有逆断面S°的正则半群，τ是R上的同余，若τ满足

则称τ为R上的正规同余。

设λ为L上的同余，若λ满足

则称λ为L上的正规同余。

下面的定理说明正规同余正是可扩张的同余。

定理1设S是具有逆断面S°的正则半群，τ为R上的同余，则τ是正规的当且仅当τ能扩张到S上。

证明 若τ能扩张到S上，则显然τ是正规的。反之，设τ为R上的正规同余，定义S上的关系ρ为

易见，ρ是S上的等价关系。设x ρ y，t∈S。对任意a∈R，注意到

于是，（atx）°°=（at）°°（at）°（（at）°°（at）°atx）°°。而x ρ y，（at）°°（at）°（at）∈R，由ρ的定义，有

又，（at）°°（at）°∈E（S°）⊆R，τ是R上的同余，故

即（atx）°°（atx）°atx τ（aty）°°（aty）°aty。因此，tx ρ ty。另一方面，注意到

从而，（axt）°°=（ax）°°（ax）°（（ax）°°（ax）°axtt°）°°t°°。由x ρ y，知

又，t°°∈I，由τ的正规性，有

及（（ax）°°（ax）°（ax）·tt°）°τ（（ay）°°（ay）°（ay）·tt°）°，从而

因为（（ax）°°（ax）°（ax）τ（ay）°°（ay）°（ay），由引理2，有

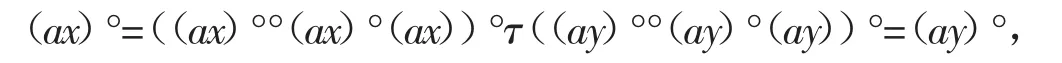
所以

注意到t°°t°∈E（S°）⊆R，t°°t°t∈R，τ为R上的同余，故

即（axt）°°（axt）°（axt）τ（ayt）°°（ayt）°（ayt），从而xt ρ yt。因此，ρ是S上的同余。

对偶地，若λ为L上的同余，则λ是正规的当且仅当λ可扩张到S上。

证明 设a，b∈R，若aτb，则aτ*b，从而。反之，若即aτ*b，则存在s1，…，sn，t1，R，使得

其中（xi，yi）∈τ（i=1，2，…，n）。由假设，τ是R上的正规同余，故存在ρ∈C（S），使得（i=1，2，…，n），则（xi，yi）∈ρ（i=1，2，…，n），于是（sixiti，siyiti）∈ρ（i=1，2，…，n），从而

引理3设S为具有逆断面S°的正则半群，则对任意ρ，σ∈C（S），有

因此，

证明 设ρ1⊆σ1，ρR⊆σR，x，y∈S，且xρy，则x°ρ°y°，x°°ρ°y°°，从而xx°ρyy°，x°°x°x ρy°°y°y。而ρ1⊆σ1，ρR⊆σR，故，xx°σyy°，x°°x°x σy°°y°y，从而xx°·x°°x°x σyy°·y°°y°y，即xσy，从而ρ⊆σ。反之，若ρ⊆σ，易见ρ1⊆σ1，ρR⊆σR。

定义2设S为具有逆断面S°的正则半群，τI、τR分别为I、R上的正规同余且满足

则称（τI，τR）为S上的IR－同余对。定义S上的关系ρ（τI，τR）为

下面的引理是对上面的定义作进一步的解释。

引理4设（τI，τR）为S上的IR－同余对，则

证明 设e°，f°∈E（S°）。若e°τIf°，由定义2，（e°e°）°τR（e°f°）°，即e°τRe°f°。同理，（f°e°）°τR（f°f°）°，即f°e°τRf°。故。若e°τRf°，由定义2，（e°e°）（e°e°）°τI（f°e°）（f°e°）°，即于是

下面给出S上同余的第1种刻画。

定理2设S是具有逆断面S°的正则半群，对S上的任一IR－同余对（τI，τR），关系ρ（τI，τR）为使在I、R上的限制分别为τI、τR的惟一同余。反之，S上任一同余都可以如此构造。

证明 设（τI，τR）是S上一IR－同余对，记ρ（τI，τR）=ρ。易见ρ是S上的等价关系。设x，y∈S且xρy，则xx°τIyy°，x°°x°x τRy°°y°y。对任意z∈S，首先，由定义2知

又，xx°τIyy°，由引理2知，x°°x°=（xx°）°τI（yy°）°=y°°y°，而τI是I上的同余，故

即（xz）（xz）°τI（yz）（yz）°。另一方面，注意到

（x°°x°xzz°）°°τR（y°°y°yzz°）°°，而x°°x°τIy°°y°，由引理4，x°°x°τRy°°y°。又，x°°x°x τRy°°y°y，由τR是R上的正规同余，得（x°°x°xzz°）°（x°°x°xzz°）τR（y°°y°yzz°）°（y°°y°yzz°）。而z°°z°∈E（S°）⊆R，z°°z°z∈R，τR∈C（R），于是

即（xz）°°（xz）°（xz）τR（yz）°°（yz）°（yz）。故，xzρyz。

其次，因为xx°τIyy°，由τI的正规性得（z°zxx°）（z°zxx°）°τI（z°zyy°）（z°zyy°）°。再由τI的正规性，得z°°（z°zxx°）（z°zxx°）°z°τIz°°（z°zyy°）（z°zyy°）°z°。而zz°∈I，τI是I上的同余，故

即（zx）（zx）°τI（zy）（zy）°。另一方面，注意到

由xx°τIyy°及定义2得

从而（z°°z°zxx°）°°τR（z°°z°zyy°）°°。而x°°x°τIy°°y°，由引理4得，x°°x°τRy°°y°。又，z°°z°∈E（S°）⊆R，τR∈C（S），于是，有

即（zx）°°（zx）°（zx）τR（zy）°°（zy）°（zy）。所以，zxρzy，从而ρ是S上的同余。

设e，f∈I，若e ρIf，即e ρIf，则e ρ f，因此ee°τIff°，即e τIf。反之，若e τIf，由引理2，e°τIf°；由引理4，e°τRf°。从而ee°e°e=e°τRf°=f°°f°f，进而e ρ f，即e ρIf，所以ρI=τI。设a，b∈R，若a τRb，由引理1，a ρRb，从而a ρ b，因此a°°a°a τRb°°b°b，即a τRb。反之，若a τRb，即a°°a°a τRb°°b°b，由引理2，a°τRb°，从而a°°a°τRb°°b°。而a°°a°=a°°a°aa°=aa°，b°°b°=b°°b°bb°=bb°，所以aa°τRbb°。又，aa°=a°°a°，bb°=b°°b°∈E（S°）。由引理4，aa°τIbb°。于是，aρb，从而aρRb，ρR=τR。

反之，设σ∈C（S），易证（σI，σR）是IR－同余对，由前述的证明可知，ρ（σI，σR）是同余。易见σ⊆ρ（σI，σR）。设x ρ（σI，σR）y，则xx°σIyy°，x°°x°x σRy°°y°y，即x°°x°x σ y°°y°y，于是，x=xx°·x°°x°x σ yy°·y°°y°y，从而σ=ρ（σI，σR）。

若S是具有Q－逆断面S°的正则半群，则定义2的条件可用下列条件代替

由定理2，对任一同余ρ，可得IR－同余对Jρ=（ρI，ρR）。反之，对任一IR－同余对，存在同余ρJ与之相对应。由此可见是互逆的映射，且ρJρ=ρ，JρJ=J。

记S上的IR－同余对的集合为CPIR（S），定义CPIR（S）上的序≤为按分量的包含。易见，≤是CPIR（S）上的偏序。由引理3，有

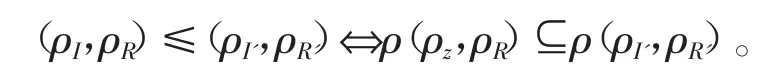
由定理2知C（S）与CPIR（S）作为偏序集同构，从而作为（完全）格同构。下面确定CPIR（S）中元素的∨和∧。

引理5设S为具有逆断面S°的正则半群，Ψ为S上的一族同余，对ρ∈Ψ，记Jρ=（ρI，ρR），则

推论2设S是具有逆断面S°的正则半群，Γ为非空的一族S的IR－同余对，记J＝（τI，τR）∈Γ，则

推论3设S是具有逆断面S°的正则半群，则CPIR（S）关于偏序≤是一个格，且CPIR（S）中的运算为

证明 由C（S）与CPIR（S）间为格同构及引理5、推论2可得。

针对具有逆断面S°的正则半群S的以子半群I、R为构件的结构，我们有其上同余的IR－刻画。对偶地，S的结构也可以Λ、L为构件。相应地，可以得到其上同余的第2种刻画——ΛL－刻画。

定义3设S是具有逆断面S°的正则半群，τΛ、τL分别是Λ、L上的正规同余且满足

则称（τL，τΛ）为S上的ΛL－同余对。定义S上的关系ρ（τΛ，τL）为

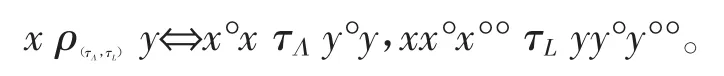
定理3设S是具有逆断面S°的正则半群，对S上的任一ΛL－同余对（τΛ、τL），关系ρ（τΛ，τL）是使在Λ、L上的限制分别为τΛ、τL的惟一同余。反之，S上的任一同余都可以如此构造。

我们还可以给出具有逆断面的正则半群上同余的第3种刻画——基于以L、R为构件结构的相应的同余的刻画。

定义4设S是具有逆断面S°的正则半群，τL、τR分别为L、R上的正规同余且满足

则称（τL、τR）为S上的LR－同余对。定义S上的关系ρ（τI，τR）为

下面的引理保证定义有意义。

引理6设（τL、τR）是S上的LR－同余对，则

证明 略。

定理4设S是具有逆断面S°的正则半群，（τL、τR）是S上一LR－同余对，则关系ρ（τI，τR）是使在L、R上的限制分别为τL、τR的惟一同余。反之，S上的任一同余均可如此构造。

证明 略。

若S是具有Q－逆断面S°的正则半群，则定义4的条件可用下列条件代替

［1］WANGLM.On Congruence Lattices ofRegular Semigroups with Q-inverse Transversals［J］.Semigroup Forum，1995，50：141 -160.

［2］TANGXL，WANGLM.Congruences on Regular Semigroups with Inverse Transversals［J］.Communications in Algebra，1995，23（11）：4157-4171.

［3］WANGLM，TANGXL.Congruence Lattices ofRegular Semigroups with Inverse Transversals［J］.Communications in Algebra，1998，26（4）：1243-1255.

［4］HOWIE J M.Fundamentals ofSemigroup Theory［M］.London：Clarendon Press，1995.

［5］PASTIJNF，PETRICH M.Congruences on Regular Semigroups［J］.Tran Amer Math Soc，1986，295（2）：607-633.

［6］SAITOT.Construction ofRegular Semigroups with Inverse Transversals［J］.Proc Edinburgh Math Soc，1989，32：41-51.

［7］TANGXL.Regular Semigroups with Inverse Transversals［J］.Semigroup Forum，1997，55：24-32.

［8］SAITOT.ANote on Regular Semigroups with Inverse Transversals［J］.Semigroup Forum，1986，33：149-152.

［9］PASTIJN F，PETRICH M.The Congruence Lattice ofa Regular Semigroup［J］.Journal ofPure and Applied Algebra，1988，53：93-123.

【责任编辑：王桂珍foshanwgzh@163.com】

Congruences on regular semigroups with inverse transversals

FENGYing-ying，SHANGYu

（1.School ofMathematics and Data，Foshan University，Foshan 528000，China；2.School ofMathematics and Statistics，Puer University，Puer 665000，China）

It is presented three ways of characterization of congruences on regular semigroups with inverse transversal：LR，ΛL and LR.

inverse transversal；regular semigroup；congruences；characterization

O152.7

A

1008-0171（2016）04-0001-07

2016-03-26

佛山科学技术学院优秀青年教师培养计划资助项目（fsyq201408）

冯莹莹（1980-），女，广东广州人，佛山科学技术学院讲师，博士。